Thompsons Experiment Rutherfords Experiment Explanation Diffraction the change

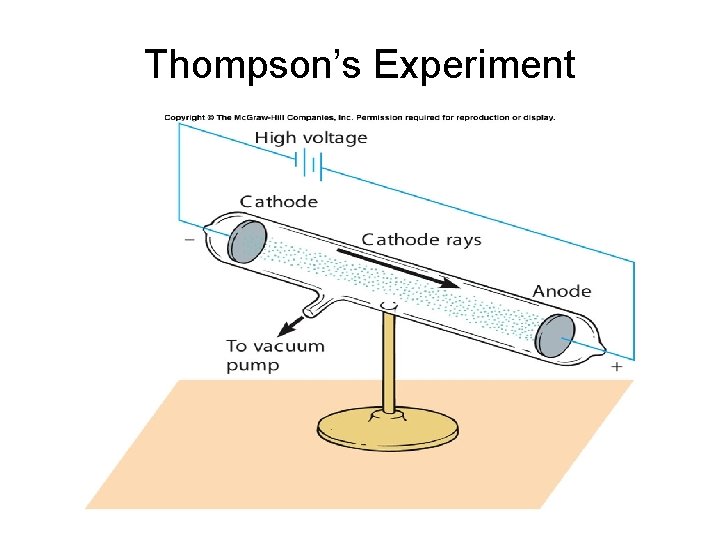
Thompson’s Experiment

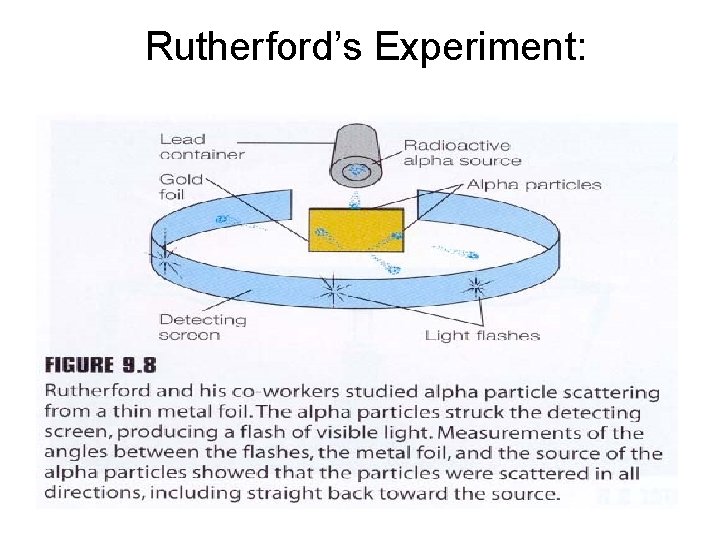
Rutherford’s Experiment:

Explanation

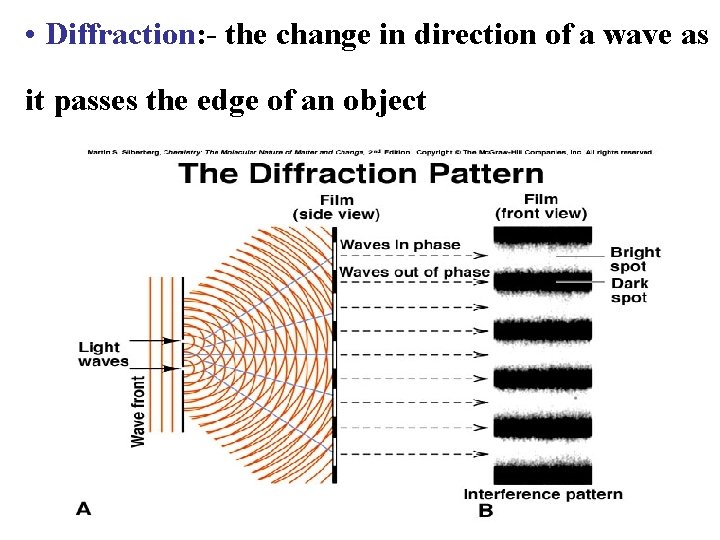
• Diffraction: - the change in direction of a wave as it passes the edge of an object

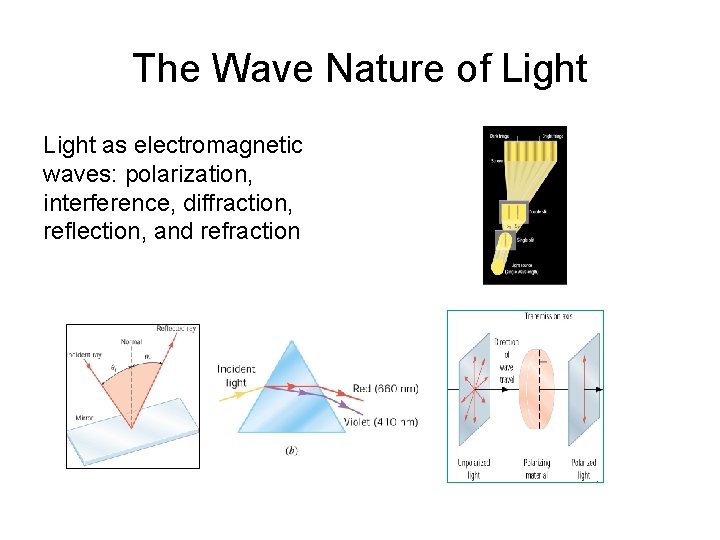
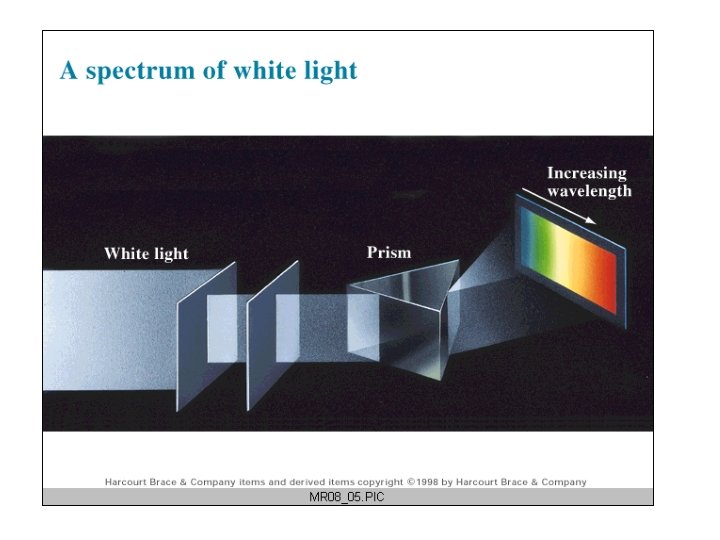
The Wave Nature of Light as electromagnetic waves: polarization, interference, diffraction, reflection, and refraction

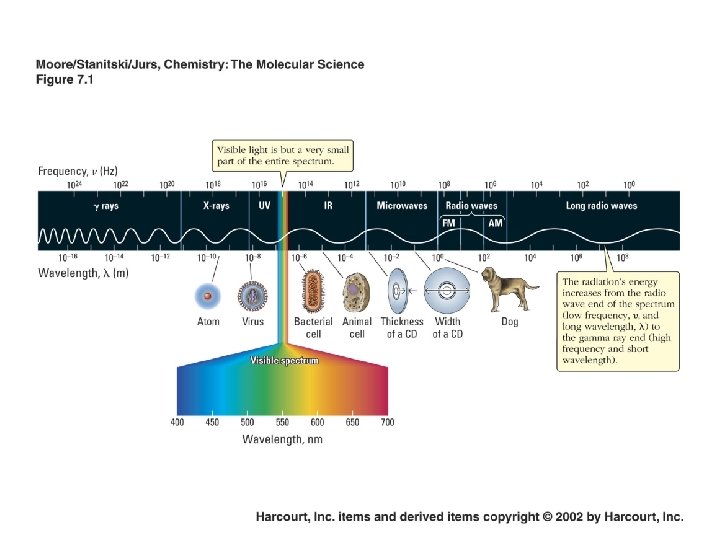
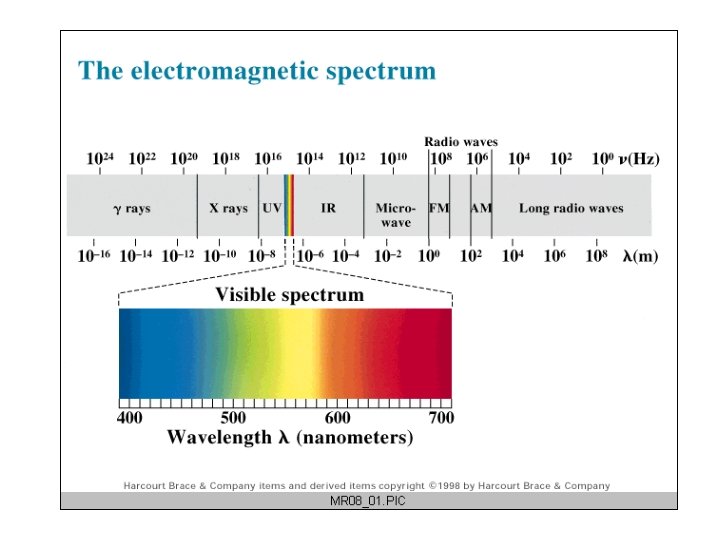
Electromagnetic Spectrum

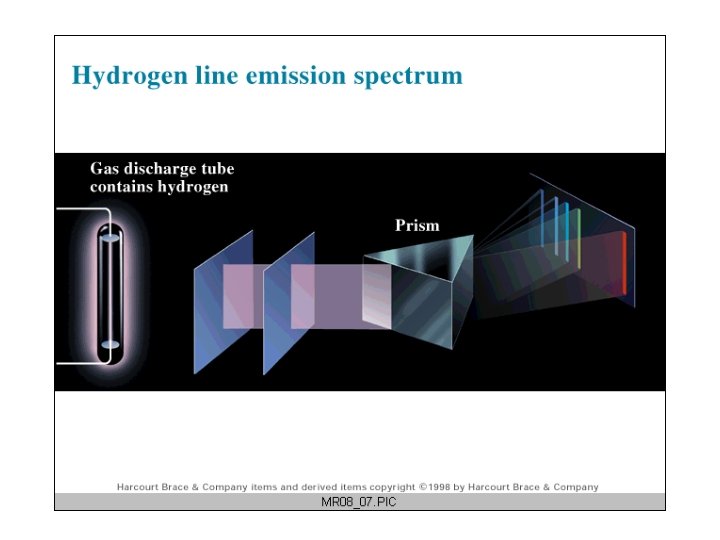
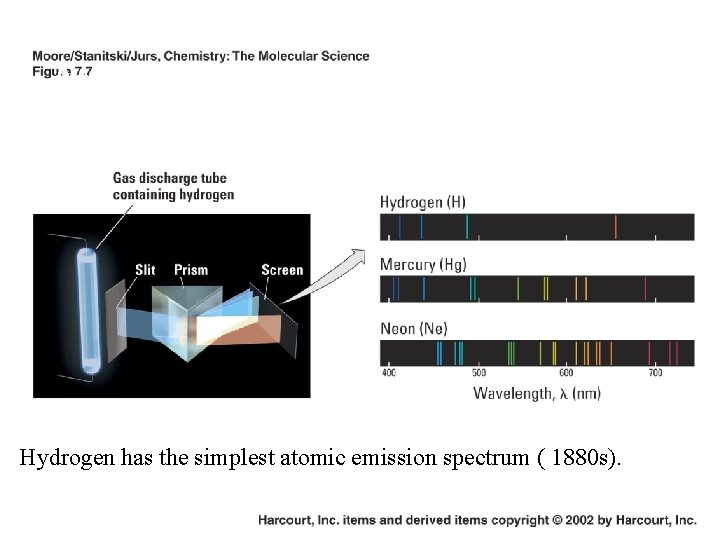
Atomic Line Spectra (Line Emission Spectra) Hydrogen has the simplest atomic emission spectrum ( 1880 s).

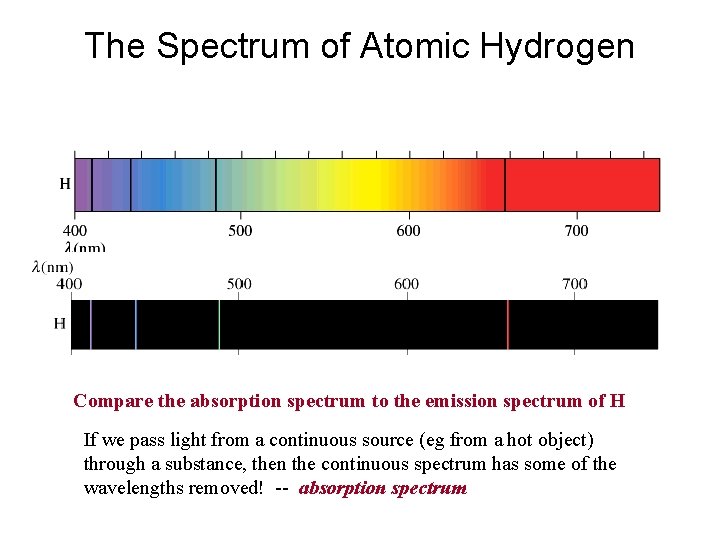
The Spectrum of Atomic Hydrogen Compare the absorption spectrum to the emission spectrum of H If we pass light from a continuous source (eg from a hot object) through a substance, then the continuous spectrum has some of the wavelengths removed! -- absorption spectrum

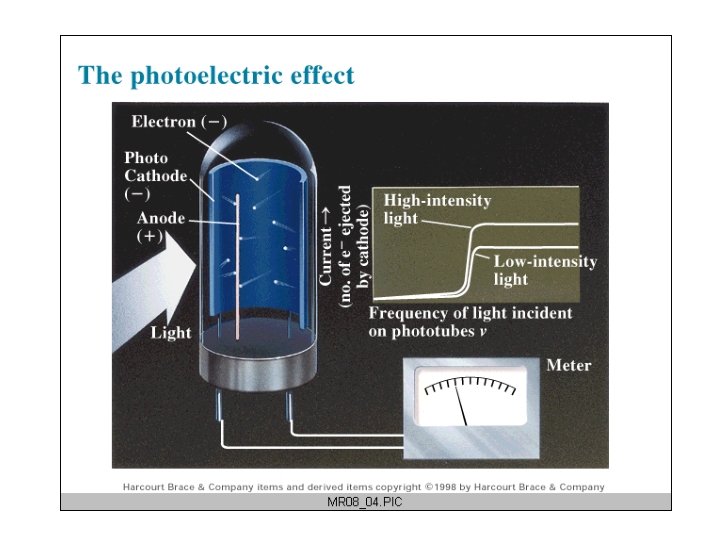
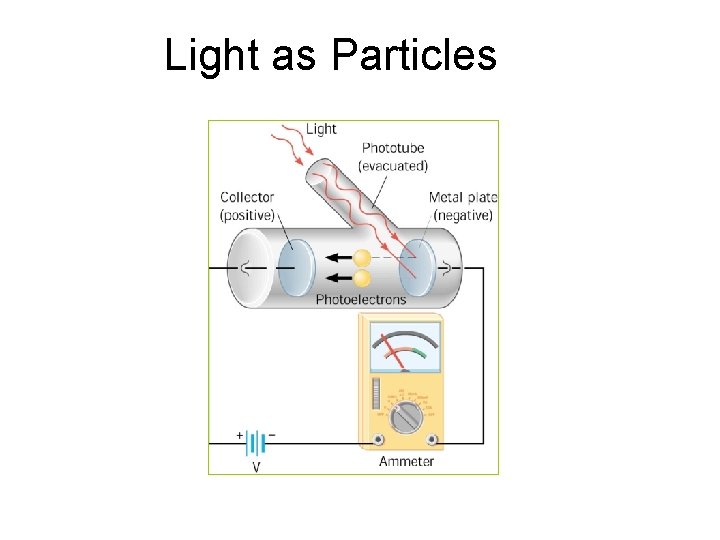
Light as Particles

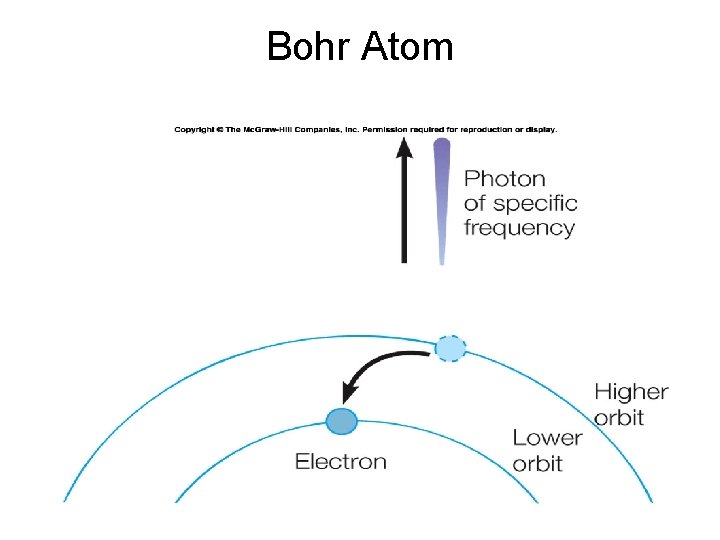
Bohr Atom

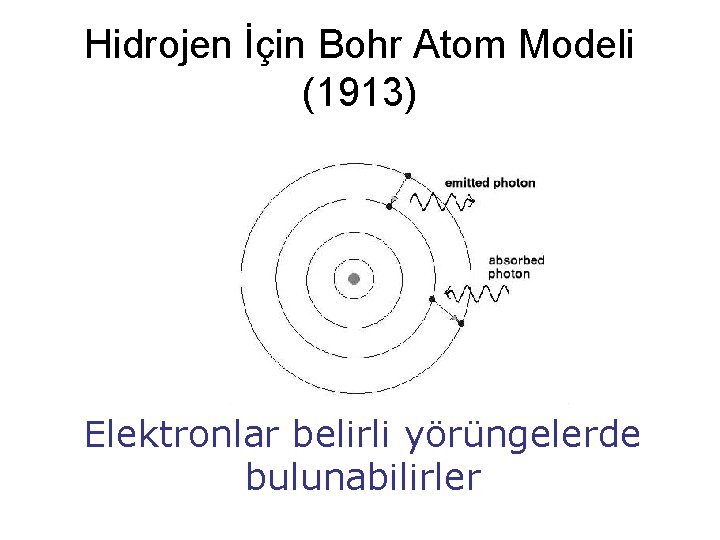
Hidrojen İçin Bohr Atom Modeli (1913) Elektronlar belirli yörüngelerde bulunabilirler

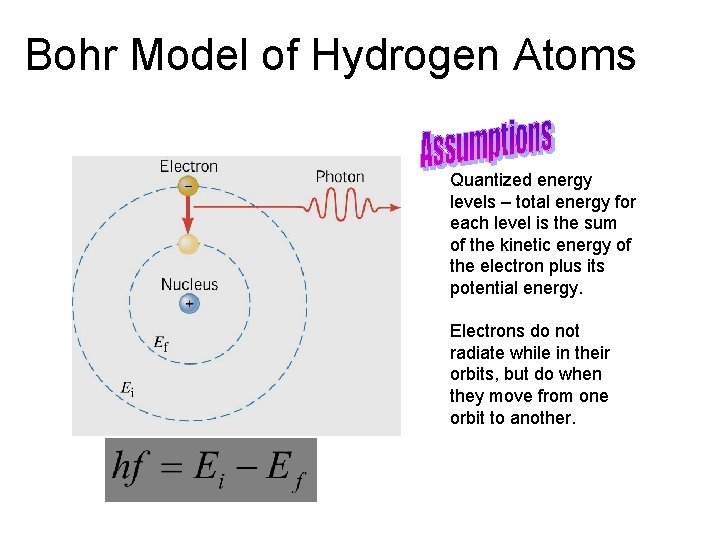
Bohr Model of Hydrogen Atoms Quantized energy levels – total energy for each level is the sum of the kinetic energy of the electron plus its potential energy. Electrons do not radiate while in their orbits, but do when they move from one orbit to another.

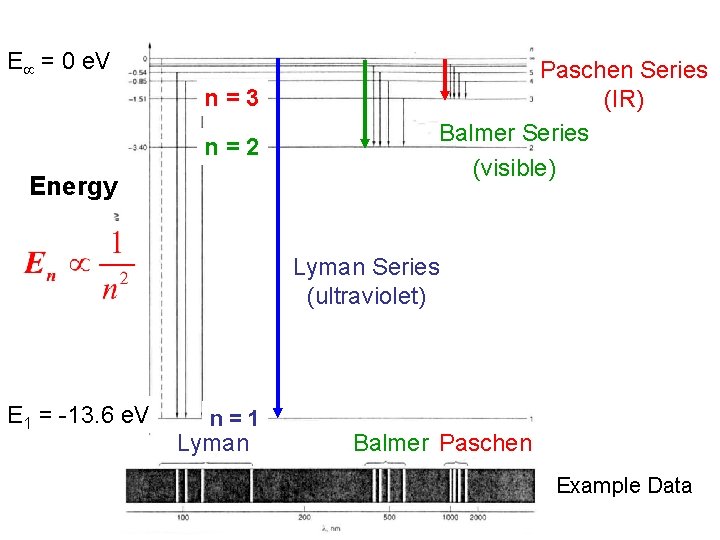
E = 0 e. V n=3 n=2 Energy Paschen Series (IR) Balmer Series (visible) Lyman Series (ultraviolet) E 1 = -13. 6 e. V n=1 Lyman Balmer Paschen Example Data

Line Spectra The Lyman and Balmer series of lines in the hydrogen spectrum correspond to transitions that the electrons make between higher and lower energy levels. The Bohr model only has one quantum number, n, which represents the energy level. http: //www. walter-fendt. de/ph 11 e/bohrh. htm

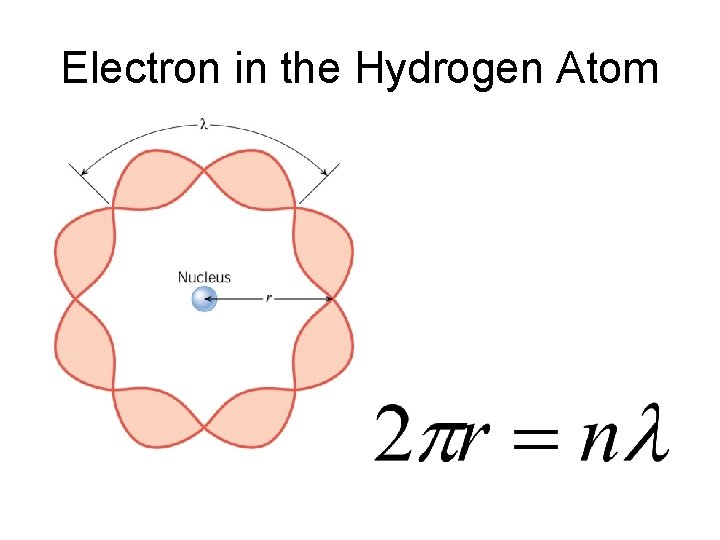
Electron in the Hydrogen Atom

• Elektronlar gerçekten de çekirdek etrafında belirli yörüngelerde mi dönerler? • Bunu tespit etmek mümkün mü?

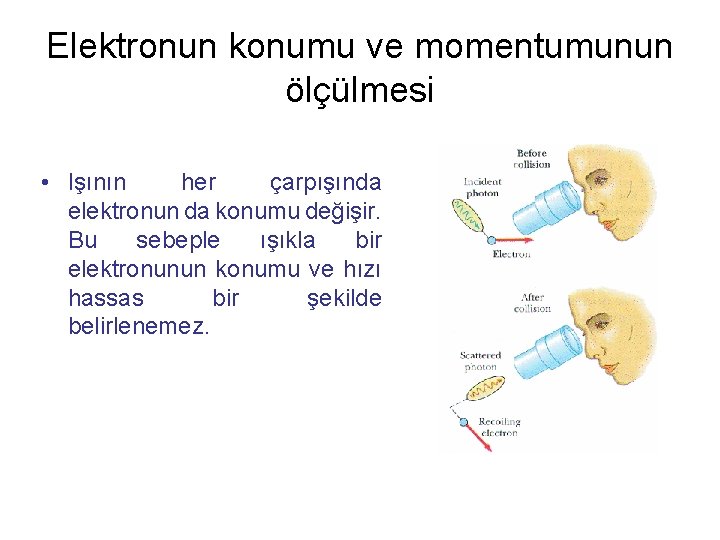
Elektronun konumu ve momentumunun ölçülmesi • Işının her çarpışında elektronun da konumu değişir. Bu sebeple ışıkla bir elektronunun konumu ve hızı hassas bir şekilde belirlenemez.

Heisenberg, Werner 1901– 76, Alman Fizikçi 1932 Nobel Fizik Ödülü Eğer bir taneciğin nerede olduğunu kesin olarak biliyorsak, aynı anda taneciğin nereden geldiğini ve nereye gittiğini kesin şekilde bilemeyiz.

Peki elektronlar nerede ve nasıl hareket ediyorlar?

Erwin Schrödinger 1927 yılında • Elektronlar, zamanlarının büyük bir çoğunluğunu orbital denen bölgelerde geçirirler. • Değişik şekillerde orbitaller mevcuttur.

Atomik Orbitaller s p d f Şekli küresel halter karışık Orbital sayısı 1 3 5 7 Herbir orbital 2 elektron içerir e sayısı 2 6 10 14

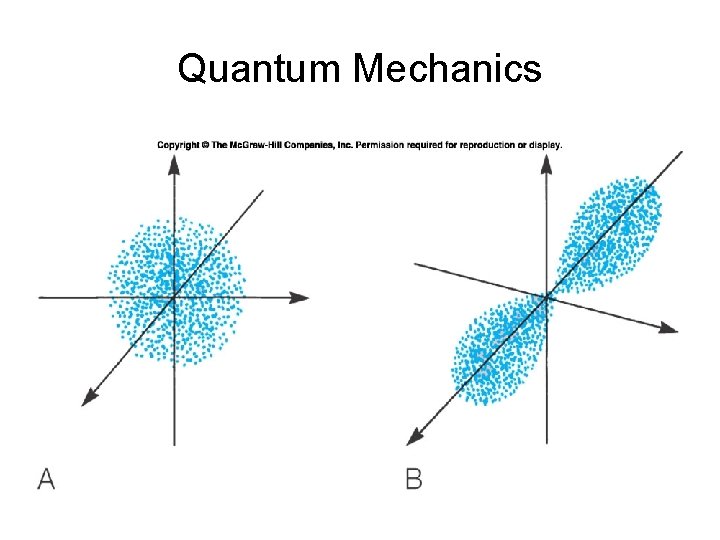
Quantum Mechanics

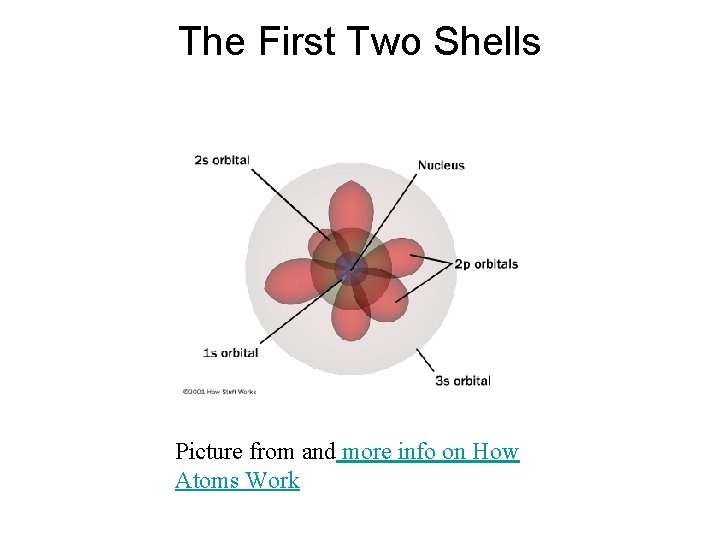
The First Shell • The innermost shell (1) only contains an s orbital. 1 s

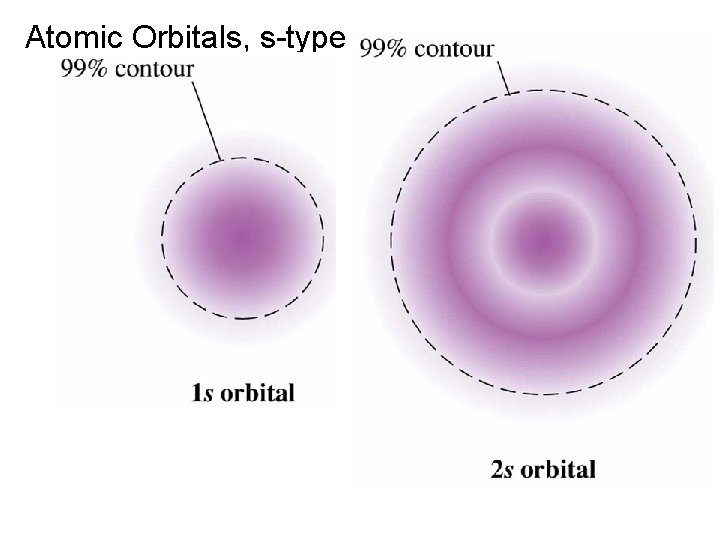
Atomic Orbitals, s-type

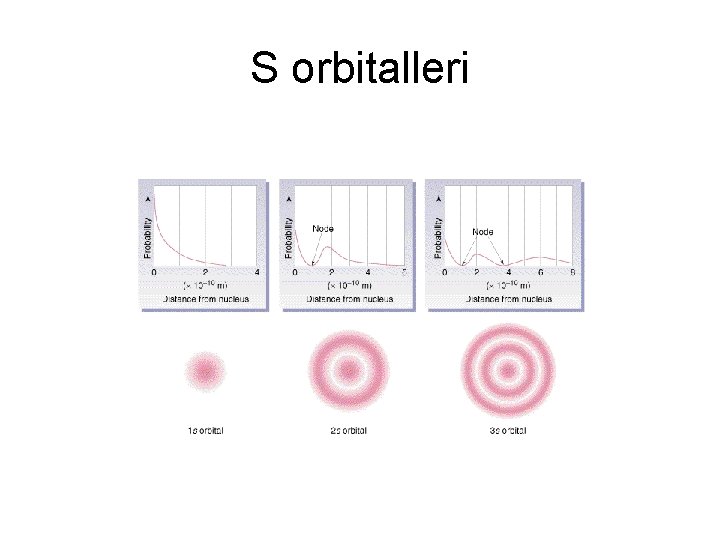
S orbitalleri

Atomic Structure

Quantum Mechanics

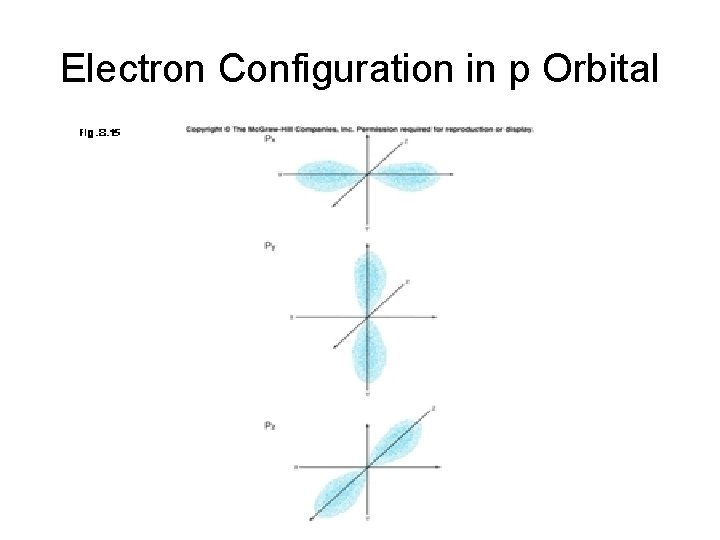
Electron Configuration in p Orbital

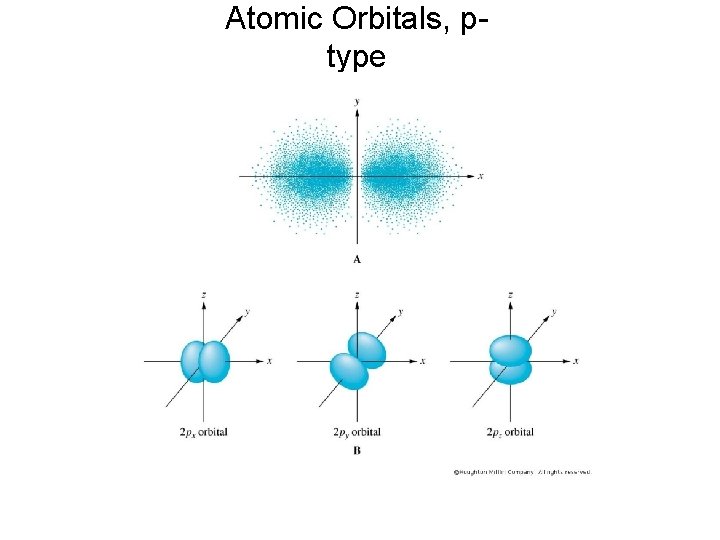
Atomic Orbitals, ptype

p Orbitals • Rather than being a sphere, the "p" orbital has two lobes pointed in opposite direction away from the nucleus. • One p orbital points along each the x, y, and z axis. • There are three p orbtitals in every shell except the first.

The Second Shell • The second shell contains an s type orbital as well as a new kind of orbital called a "p" orbital. 2 py 2 s 2 pz 2 px

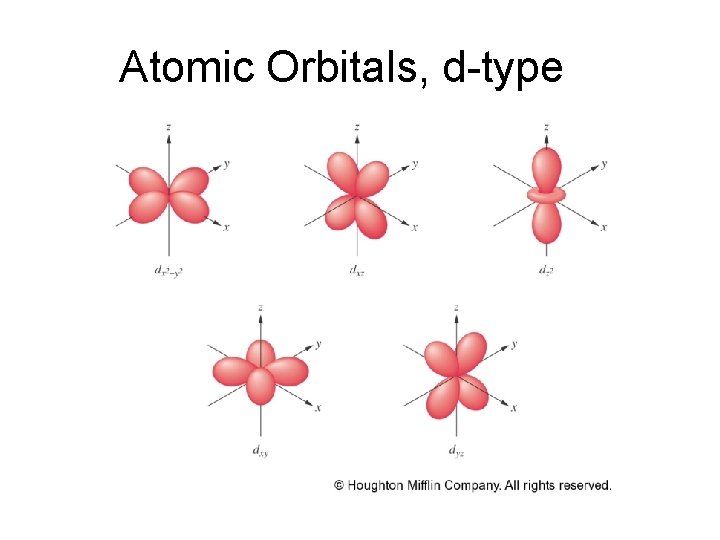
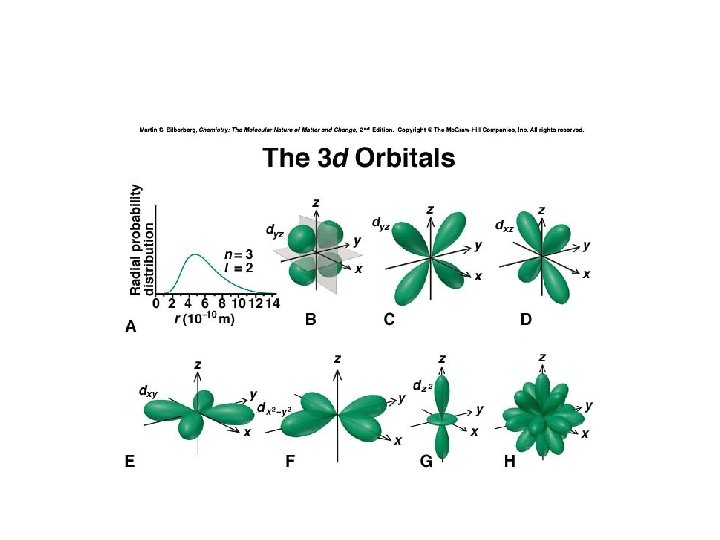
Atomic Orbitals, d-type

d Orbitals • There are 5 types of d orbitals. Four of the five have four lobes at 90 o to one another. The fifth looks like a donut around a p-orbital Image from: HMChem

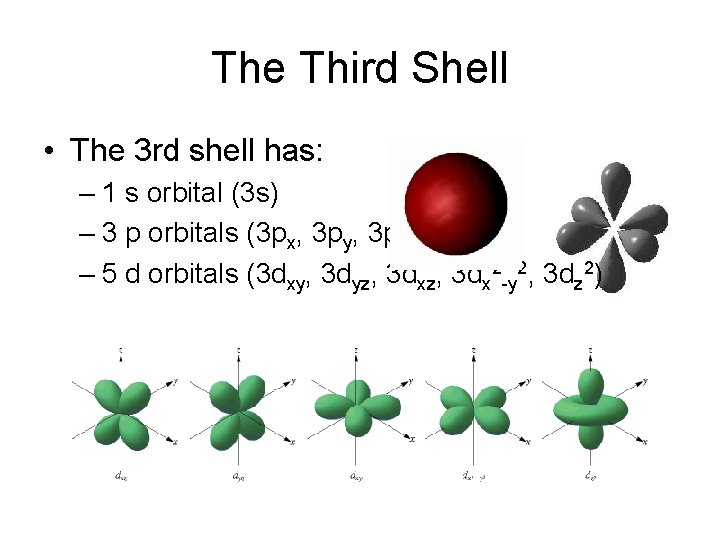
The Third Shell • The 3 rd shell has: – 1 s orbital (3 s) – 3 p orbitals (3 px, 3 py, 3 pz) – 5 d orbitals (3 dxy, 3 dyz, 3 dx 2 -y 2, 3 dz 2)

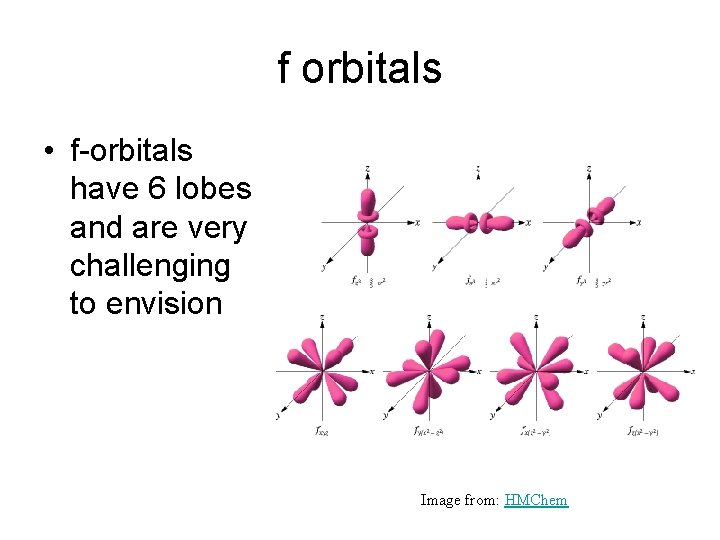
f orbitals • f-orbitals have 6 lobes and are very challenging to envision Image from: HMChem

The First Two Shells Picture from and more info on How Atoms Work

The Fouth Shell • The 4 th shell has: – 1 s orbital (4 s) – 3 p orbitals (4 px, 4 py, 4 pz) – 5 d orbitals (4 dxy, 4 dyz, 4 dx 2 -y 2, 4 dz 2) – 7 f orbitals

Principle quantum number n = 1, 2, 3, …. . describes orbital size and energy Angular momentum quantum number l = 0 to n-1 describes orbital shape Magnetic quantum number ml = l, l-1…-l describes orientation in space of the orbital relative to the other orbitals in the atom Spin quantum number ms = +1/2 or -1/2 describes the direction of spin of the e- on its axis Pauli Exclusion Principle: "no two electrons in an atom can have the same set of quantum numbers", or, only two electrons (of opposite spin) per orbital.

Write a valid set of quantum numbers for each of the following sub-shells: (a) 2 s n = 2, l = 0, ms = - 1/2 n = 2, l = 0, ms = ± 1/2 2 combinations

Write a valid set of quantum numbers for each of the following sub-shells: (a) 2 s n = 2, l = 0, ms = - 1/2 n = 2, l = 0, ms = ± 1/2 2 combinations (b) 2 p n = 2, l = 1, ml = -1, ms = - 1/2 n = 2, l = 1, ml = -1, 0 or 1, ms = ± 1/2 6 combinations

Write a valid set of quantum numbers for each of the following sub-shells: (a) 2 s n = 2, l = 0, ms = - 1/2 n = 2, l = 0, ms = ± 1/2 2 combinations (b) 2 p n = 2, l = 1, ml = -1, ms = - 1/2 n = 2, l = 1, ml = -1, 0 or 1, ms = ± 1/2 6 combinations (c) 3 d n = 3, l = 2, ml = -2, ms = - 1/2 n = 3, l = 2, ml = -2, -1, 0, 1, or 2, ms = ± 1/2 10 combinations

How many orbitals in a subshell? l = 0, 1 s 1 l = 1, p x, p y, p z 3 l = 2, dxy, , dxz, , dyz , , dx 2 -y 2, dz 2 5

How many orbitals in a subshell? l = 0, 1 s 1 l = 1, p x, p y, p z 3 l = 2, dxy, , dxz, , dyz , , dx 2 -y 2, dz 2 5 2 l + 1 orbitals per subshell

How many orbitals in a subshell? l = 0, 1 s 1 l = 1, p x, p y, p z 3 l = 2, dxy, , dxz, , dyz , , dx 2 -y 2, dz 2 5 2 l + 1 orbitals per subshell How many orbitals in a shell? n = 1, 1 s 1 n = 2, 2 s, 2 px, 2 py, 2 pz 4 n = 3, 3 s, 3 px, 3 py, 3 pz, 3 dxy, , 3 dxz, , 3 dyz , , 3 dx 2 -y 2, 3 dz 2 9

How many orbitals in a subshell? l = 0, 1 s 1 l = 1, p x, p y, p z 3 l = 2, dxy, , dxz, , dyz , , dx 2 -y 2, dz 2 5 2 l + 1 orbitals per subshell How many orbitals in a shell? n = 1, 1 s 1 n = 2, 2 s, 2 px, 2 py, 2 pz 4 n = 3, 3 s, 3 px, 3 py, 3 pz, 3 dxy, , 3 dxz, , 3 dyz , , 3 dx 2 -y 2, 3 dz 2 9 n 2 orbitals per principal quantum level

Hydrogen atoml all orbitals within a shell have the same energy l electrostatic interaction between e- and proton

Hydrogen atoml all orbitals within a shell have the same energy l electrostatic interaction between e- and proton Multi-electron atomsthe energy level of an orbital depends not only on the shell but also on the subshell l l electrostatic interactions between e- and proton and other e-

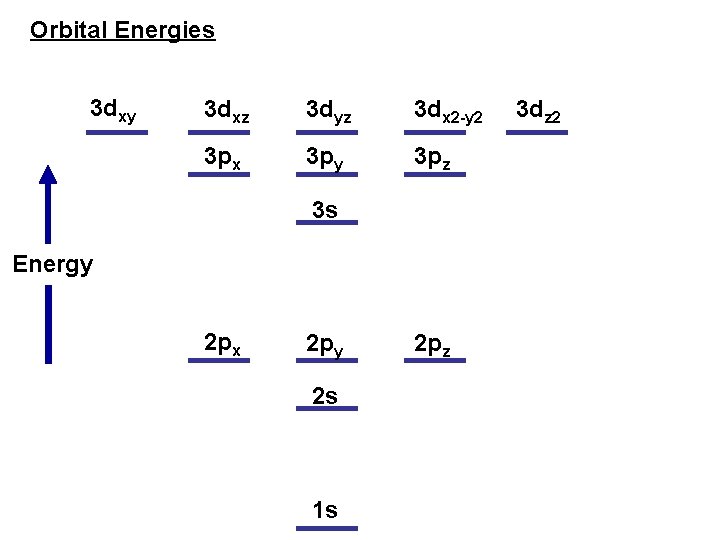
Orbital Energies 3 dxy 3 dxz 3 dyz 3 dx 2 -y 2 3 px 3 py 3 pz 3 s Energy 2 px 2 py 2 s 1 s 2 pz 3 dz 2

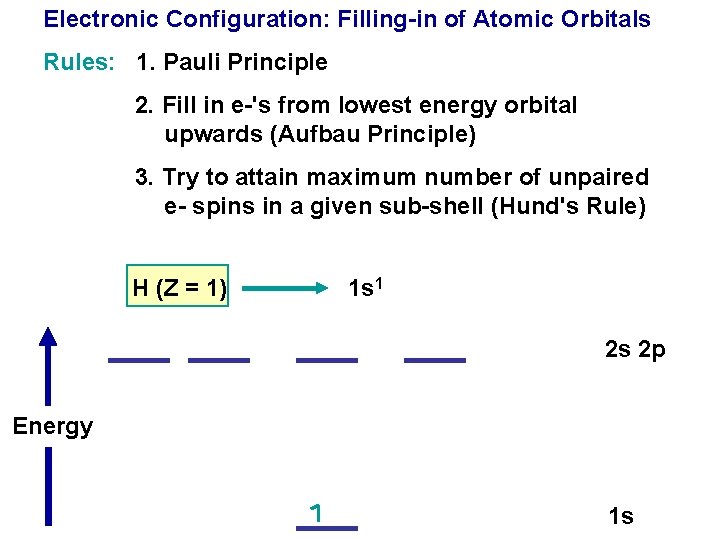
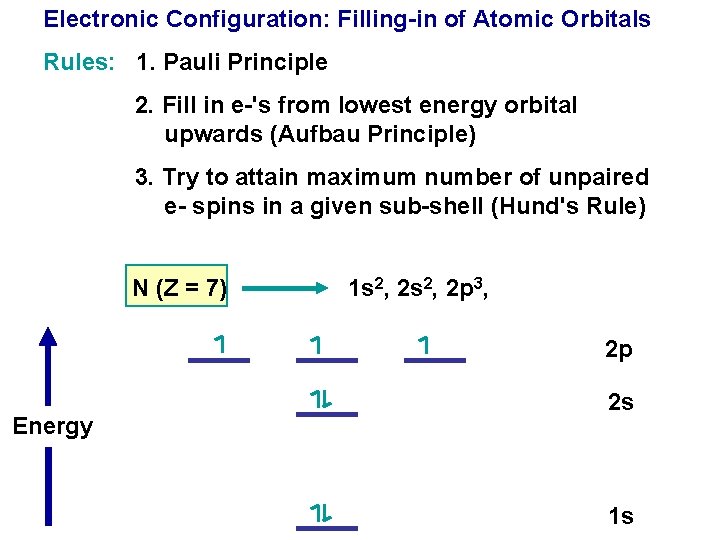
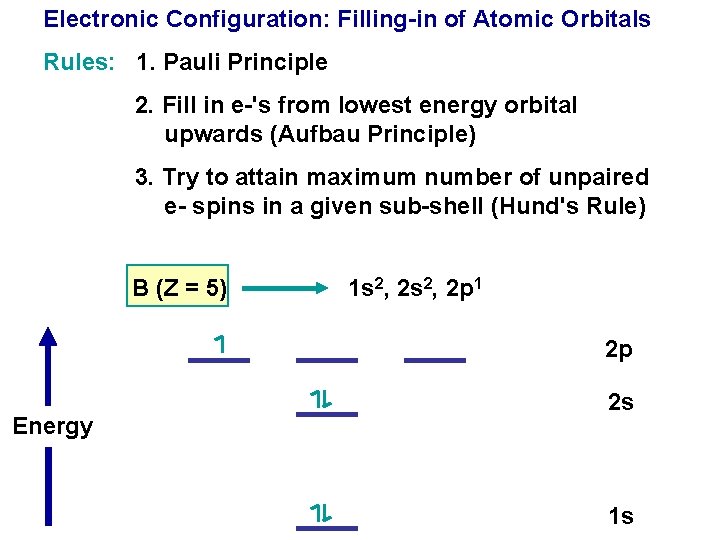
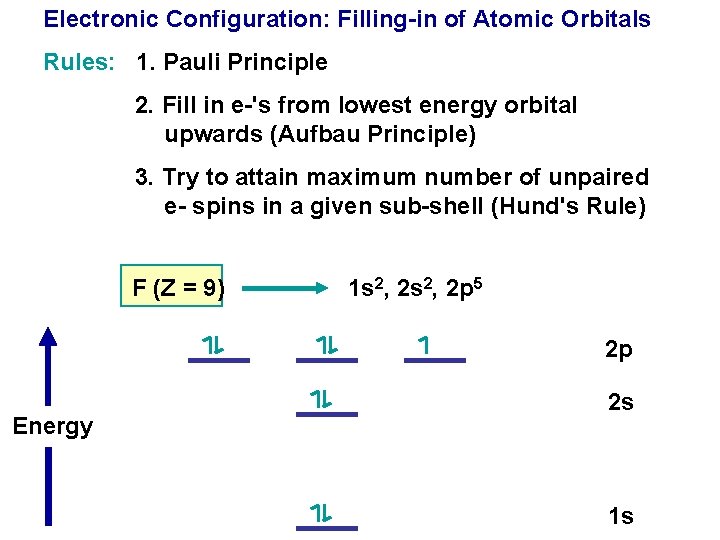
Electronic Configuration: Filling-in of Atomic Orbitals Rules: 1. Pauli Principle

Electronic Configuration: Filling-in of Atomic Orbitals Rules: 1. Pauli Principle 2. Fill in e-'s from lowest energy orbital upwards (Aufbau Principle)

Electronic Configuration: Filling-in of Atomic Orbitals Rules: 1. Pauli Principle 2. Fill in e-'s from lowest energy orbital upwards (Aufbau Principle) 3. Try to attain maximum number of unpaired e- spins in a given sub-shell (Hund's Rule)

Electronic Configuration: Filling-in of Atomic Orbitals Rules: 1. Pauli Principle 2. Fill in e-'s from lowest energy orbital upwards (Aufbau Principle) 3. Try to attain maximum number of unpaired e- spins in a given sub-shell (Hund's Rule) H (Z = 1) 1 s 1 2 s 2 p Energy 1 s

Electronic Configuration: Filling-in of Atomic Orbitals Rules: 1. Pauli Principle 2. Fill in e-'s from lowest energy orbital upwards (Aufbau Principle) 3. Try to attain maximum number of unpaired e- spins in a given sub-shell (Hund's Rule) N (Z = 7) 1 s 2, 2 p 3, 2 p Energy 2 s 1 s

Electronic Configuration: Filling-in of Atomic Orbitals Rules: 1. Pauli Principle 2. Fill in e-'s from lowest energy orbital upwards (Aufbau Principle) 3. Try to attain maximum number of unpaired e- spins in a given sub-shell (Hund's Rule) B (Z = 5) 1 s 2, 2 p 1 2 p Energy 2 s 1 s

Electronic Configuration: Filling-in of Atomic Orbitals Rules: 1. Pauli Principle 2. Fill in e-'s from lowest energy orbital upwards (Aufbau Principle) 3. Try to attain maximum number of unpaired e- spins in a given sub-shell (Hund's Rule) F (Z = 9) 1 s 2, 2 p 5 2 p Energy 2 s 1 s

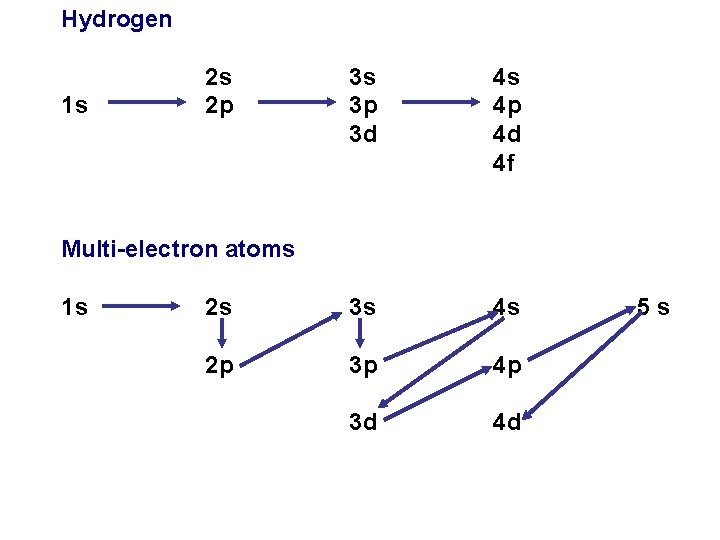
Hydrogen 1 s 2 s 2 p 3 s 3 p 3 d 4 s 4 p 4 d 4 f 2 s 3 s 4 s 2 p 3 p 4 p 3 d 4 d Multi-electron atoms 1 s 5 s

1 s H 1 s 1 He 1 s 2 Li 1 s 2, 2 s 1 Be 1 s 2, 2 s 2 B 1 s 2, 2 px 1 C 1 s 2, 2 px 1, 2 py 1 N 1 s 2, 2 px 1, 2 py 1, 2 pz 1 O 1 s 2, 2 px 2, 2 py 1, 2 pz 1 F 1 s 2, 2 px 2, 2 py 2, 2 pz 1 Ne 1 s 2, 2 px 2, 2 py 2, 2 pz 2 2 s 2 px 2 py 2 pz

H 1 s 1 He 1 s 2 Li [He], 2 s 1 Be [He], 2 s 2

H 1 s 1 He 1 s 2 Li [He], 2 s 1 Be [He], 2 s 2 B [He], 2 s 2, 2 p 1 Ne [He], 2 s 2, 2 p 6 Na [He], 2 s 2, 2 p 6, 3 s 1 [Ne], 3 s 1

H 1 s 1 He 1 s 2 Li [He], 2 s 1 Be [He], 2 s 2 B [He], 2 s 2, 2 p 1 Ne [He], 2 s 2, 2 p 6 Na [He], 2 s 2, 2 p 6, 3 s 1 [Ne], 3 s 1 Mg [He], 2 s 2, 2 p 6, 3 s 2 [Ne], 3 s 2 Al [Ne], 3 s 2, 3 p 1 Si [Ne], 3 s 2, 3 p 2

H 1 s 1 He 1 s 2 Li [He], 2 s 1 Be [He], 2 s 2 B [He], 2 s 2, 2 p 1 Ne [He], 2 s 2, 2 p 6 Na [He], 2 s 2, 2 p 6, 3 s 1 [Ne], 3 s 1 Mg [He], 2 s 2, 2 p 6, 3 s 2 [Ne], 3 s 2 Al [Ne], 3 s 2, 3 p 1 Si [Ne], 3 s 2, 3 p 2 P [Ne], 3 s 2, 3 p 3 S [Ne], 3 s 2, 3 p 4 Cl [Ne], 3 s 2, 3 p 5 Ar [Ne], 3 s 2, 3 p 6

H 1 s 1 He 1 s 2 Li [He], 2 s 1 Be [He], 2 s 2 B [He], 2 s 2, 2 p 1 Ne [He], 2 s 2, 2 p 6 Na [He], 2 s 2, 2 p 6, 3 s 1 [Ne], 3 s 1 Mg [He], 2 s 2, 2 p 6, 3 s 2 [Ne], 3 s 2 Al [Ne], 3 s 2, 3 p 1 Si [Ne], 3 s 2, 3 p 2 P [Ne], 3 s 2, 3 p 3 S [Ne], 3 s 2, 3 p 4 Cl [Ne], 3 s 2, 3 p 5 Ar [Ne], 3 s 2, 3 p 6 l l outermost shell - valence shell most loosely held electron and are the most important in determining an element’s properties

K [Ar], 4 s 1 Ca [Ar], 4 s 2 Sc [Ar], 4 s 2, 3 d 1 Ti [Ar], 4 s 2, 3 d 2

K [Ar], 4 s 1 Ca [Ar], 4 s 2 Sc [Ar], 4 s 2, 3 d 1 Ca [Ar], 4 s 2, 3 d 2 Zn [Ar], 4 s 2, 3 d 10 Ga [Ar], 4 s 2, 3 d 10, 3 p 1 Kr [Ar], 4 s 2, 3 d 10, 3 p 6

K [Ar], 4 s 1 Ca [Ar], 4 s 2 Sc [Ar], 4 s 2, 3 d 1 Ca [Ar], 4 s 2, 3 d 2 Zn [Ar], 4 s 2, 3 d 10 Ga [Ar], 4 s 2, 3 d 10, 3 p 1 Kr [Ar], 4 s 2, 3 d 10, 3 p 6 Anomalous electron configurations d 5 and d 10 are lower in energy than expected Cr [Ar], 4 s 1, 3 d 5 not [Ar], 4 s 2, 3 d 4 Cu [Ar], 4 s 1, 3 d 10 not [Ar], 4 s 2, 3 d 9

Electron Configuration of Ions Electrons lost from the highest energy occupied orbital of the donor and placed into the lowest unoccupied orbital of the acceptor (placed according to the Aufbau principle)

Electron Configuration of Ions Electrons lost from the highest energy occupied orbital of the donor and placed into the lowest unoccupied orbital of the acceptor (placed according to the Aufbau principle) Examples: Na [Ne], 3 s 1 Na+ [Ne] + e- Cl [Ne], 3 s 2, 3 p 5 + e- Cl- [Ne], 3 s 2, 3 p 6 Mg [Ne], 3 s 2 Mg 2+ [Ne] O [He], 2 s 2, 2 p 4 O 2 - [He], 2 s 2, 2 p 6

Modern Theories of the Atom - Summary n Wave-particle duality of light and matter n Bohr theory n Quantum (wave) mechanical model n Orbital shapes and energies n Quantum numbers n Electronic configuration in atoms