The General Linear Model a talk for dummies

The General Linear Model …a talk for dummies Holly Rossiter & Louise Croft Method for Dummies 2010

Topics covered • • The General Linear Model The Design Matrix Parameters Error An f. MRI example Problems with the GLM + solutions A cake recipe

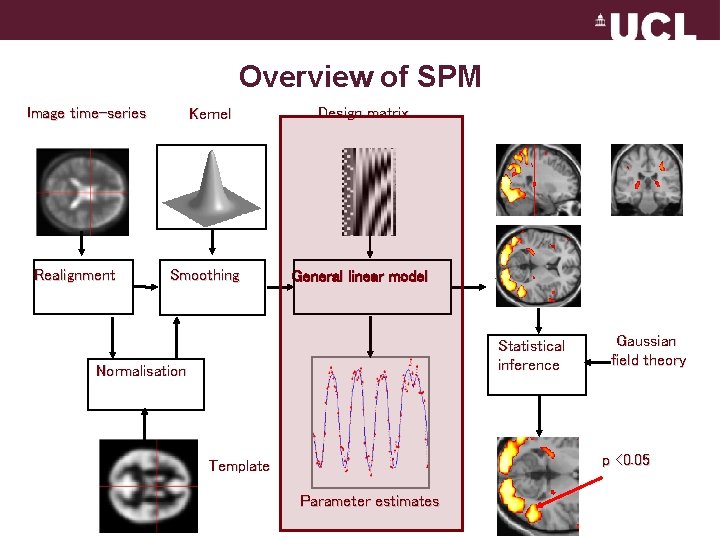
Overview of SPM Image time-series Realignment Kernel Smoothing Design matrix General linear model Statistical inference Normalisation Gaussian field theory p <0. 05 Template Parameter estimates

The General Linear Model Describes a response (y), such as the BOLD response in a voxel, in terms of all its contributing factors (xβ) in a linear combination, whilst also accounting for the contribution of error (e).

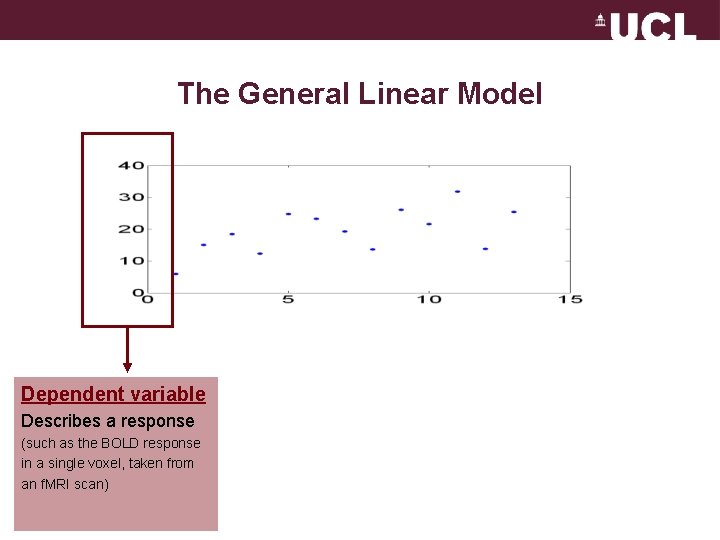
The General Linear Model Dependent variable Describes a response (such as the BOLD response in a single voxel, taken from an f. MRI scan)

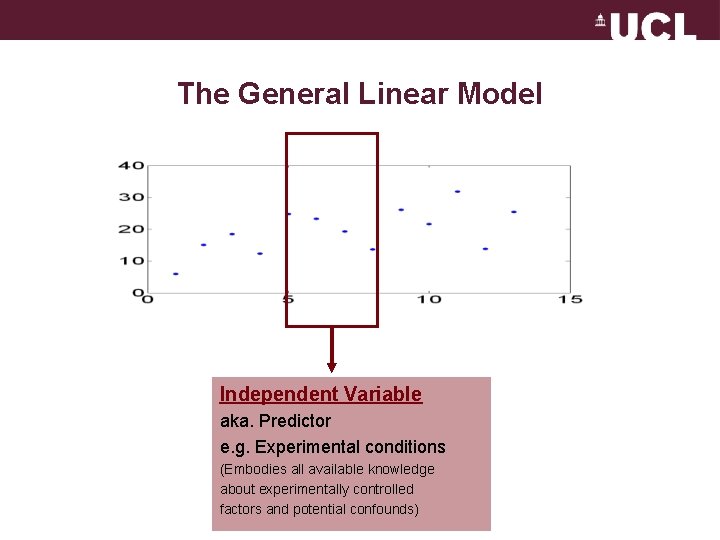
The General Linear Model Independent Variable aka. Predictor e. g. Experimental conditions (Embodies all available knowledge about experimentally controlled factors and potential confounds)

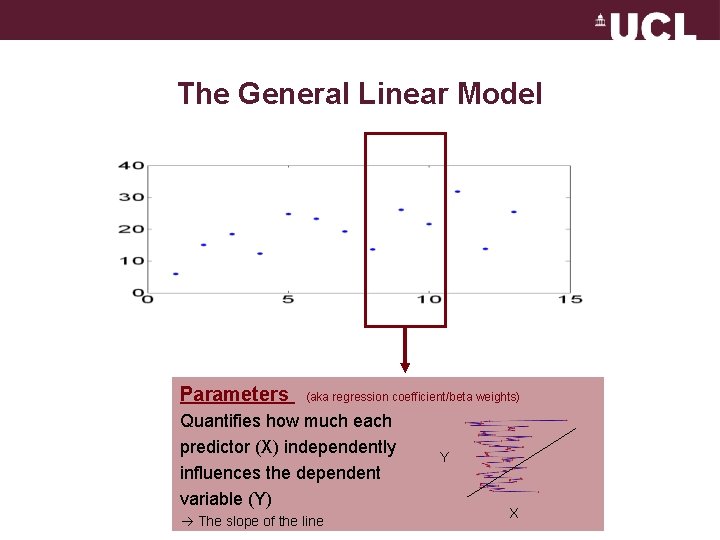
The General Linear Model Parameters (aka regression coefficient/beta weights) Quantifies how much each predictor (X) independently influences the dependent variable (Y) The slope of the line Y X

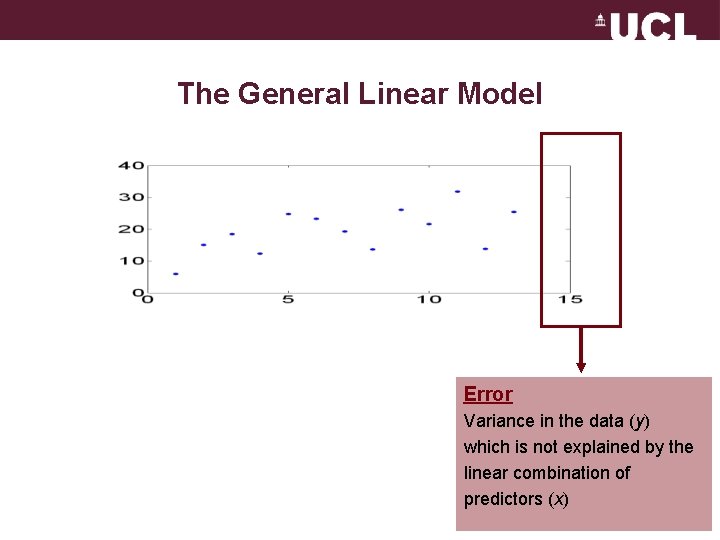
The General Linear Model Error Variance in the data (y) which is not explained by the linear combination of predictors (x)

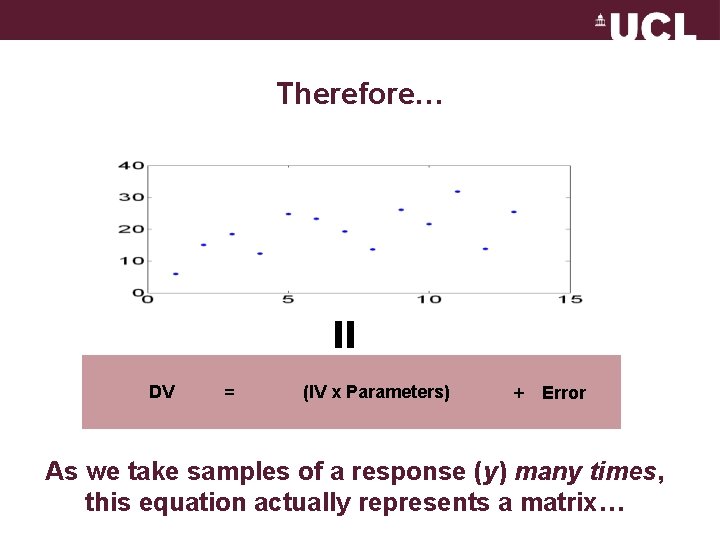
Therefore… = DV = (IV x Parameters) + Error As we take samples of a response (y) many times, this equation actually represents a matrix…

…the GLM matrix Time One response… = . . . over time Ti BOLD signal Ti m m e e Single voxel

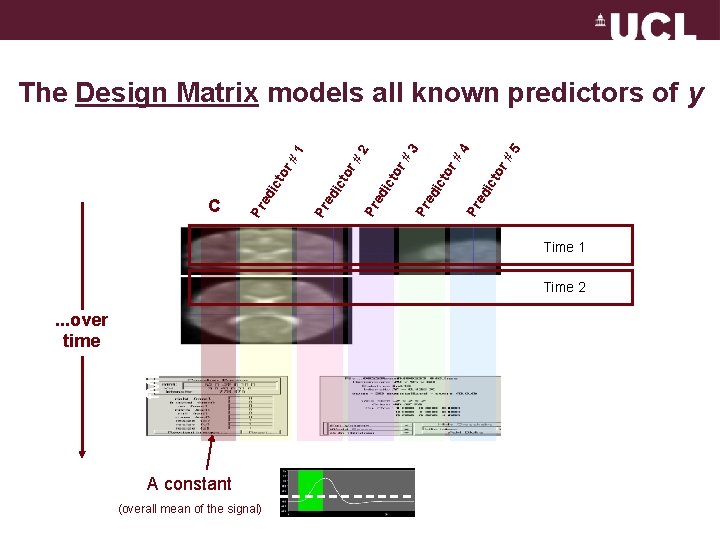
Pr ed ic to r# 5 4 r# to Pr ed ic to r# 2 Pr ed ic to r# 1 r# to Pr ed ic C 3 The Design Matrix models all known predictors of y Time 1 . . . over time f. MRI signal Time 2 A constant (overall mean of the signal)

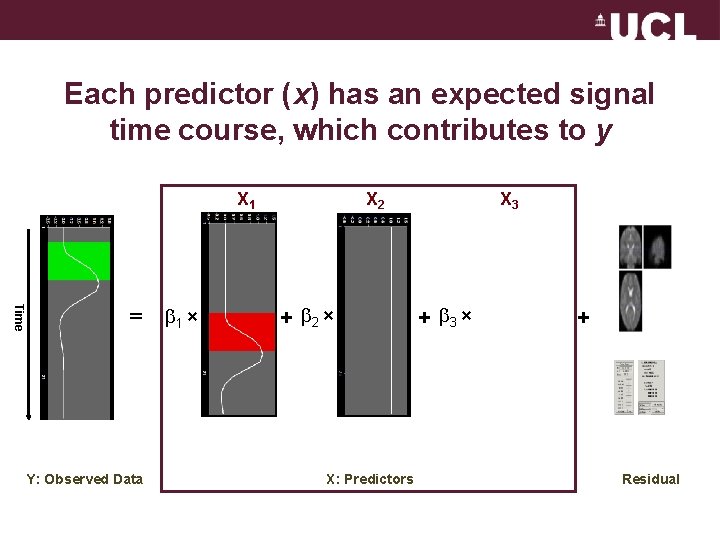
Each predictor (x) has an expected signal time course, which contributes to y X 1 Time = 1 × + 2 × f. MRI signal Y: Observed Data X 3 X 2 + 3 × + residuals X: Predictors Residual

The design matrix does not account for all of y • • If we plot our observations (n) on a graph these will not fall in a straight line Y This is a result of uncontrolled influences (other than x) on y X • This contribution to y is called the error (or residual) • Minimising the difference between the response predicted by the ^ model (y) and the actual response (y) minimises the error of the model

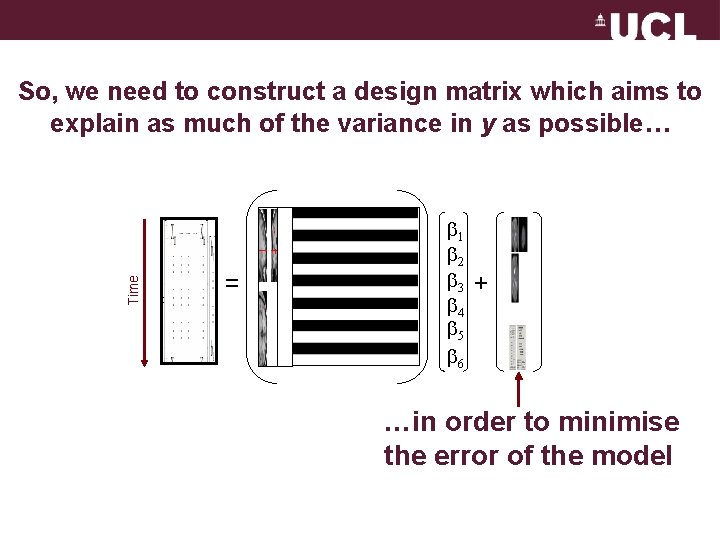
Time So, we need to construct a design matrix which aims to explain as much of the variance in y as possible… = 1 2 3 4 5 6 + …in order to minimise the error of the model

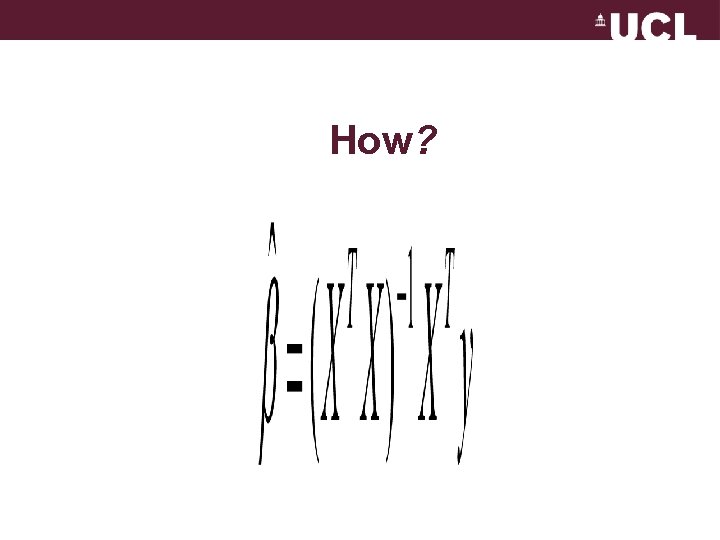
How?

Parameters (β) • Beta is the slope of the regression line Ø Quantifies a specific predictor’s (x) contribution to y. Ø The parameter (β) chosen for a model should minimise the error (reducing the amount of variance in y which is left unexplained) Y X

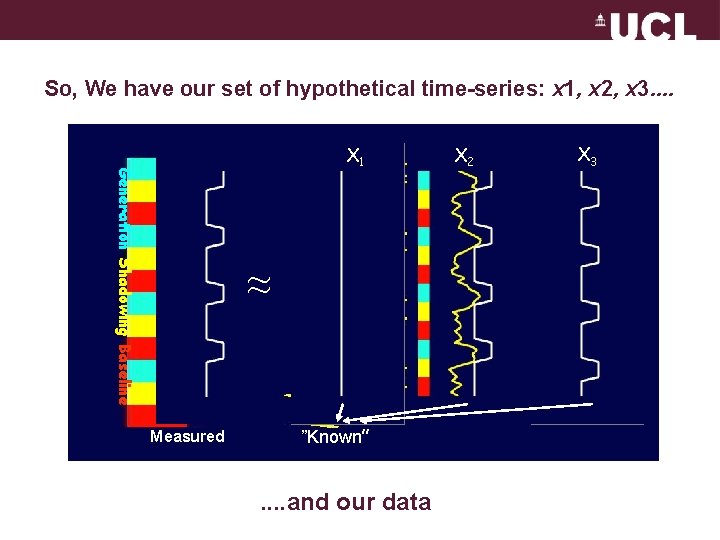
So, We have our set of hypothetical time-series: x 1, x 2, x 3. . Generation Shadowing Baseline X 1 ≈ Measured ”Known” . . and our data X 2 X 3

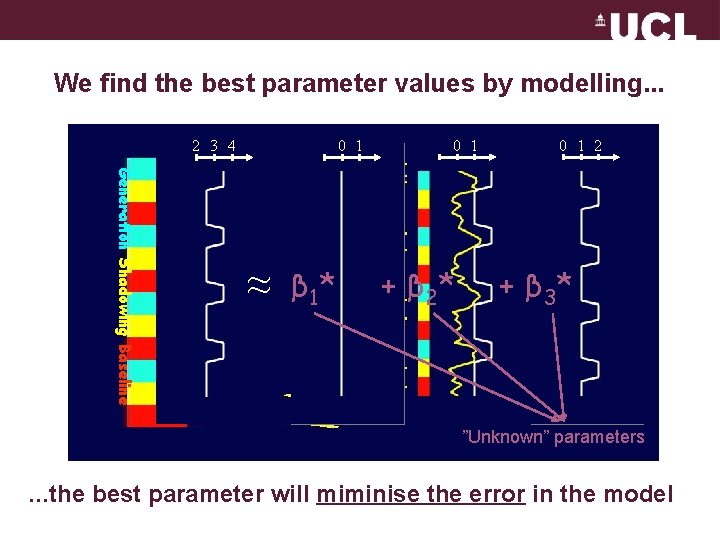
We find the best parameter values by modelling. . . 2 3 4 0 1 Generation Shadowing Baseline ≈ β 1* 0 1 + β 2* 0 1 2 + β 3* ”Unknown” parameters . . . the best parameter will miminise the error in the model

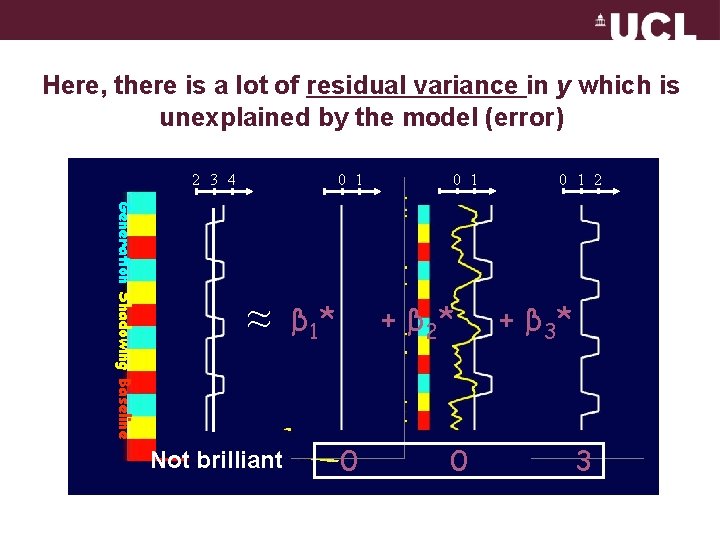
Here, there is a lot of residual variance in y which is unexplained by the model (error) 2 3 4 0 1 Generation Shadowing Baseline ≈ Not brilliant 0 1 + β 2* β 1* 0 0 0 1 2 + β 3* 3

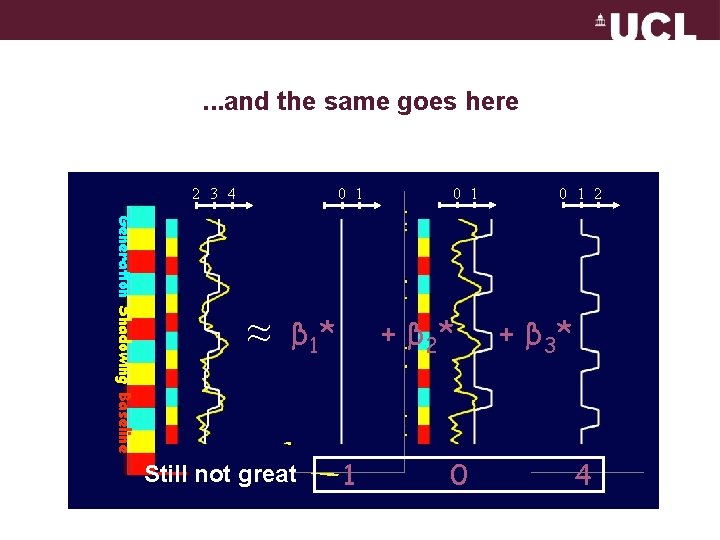
. . . and the same goes here 2 3 4 0 1 Generation Shadowing Baseline ≈ + β 2* β 1* Still not great 0 1 1 0 0 1 2 + β 3* 4

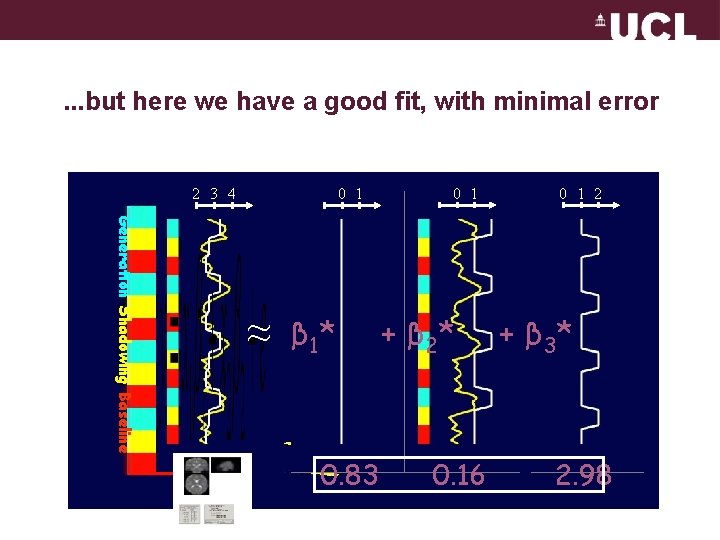
. . . but here we have a good fit, with minimal error 2 3 4 0 1 Generation Shadowing Baseline ≈ β 01* 0. 83 0 1 + β 21* 0. 16 0 1 2 + β 32* 2. 98

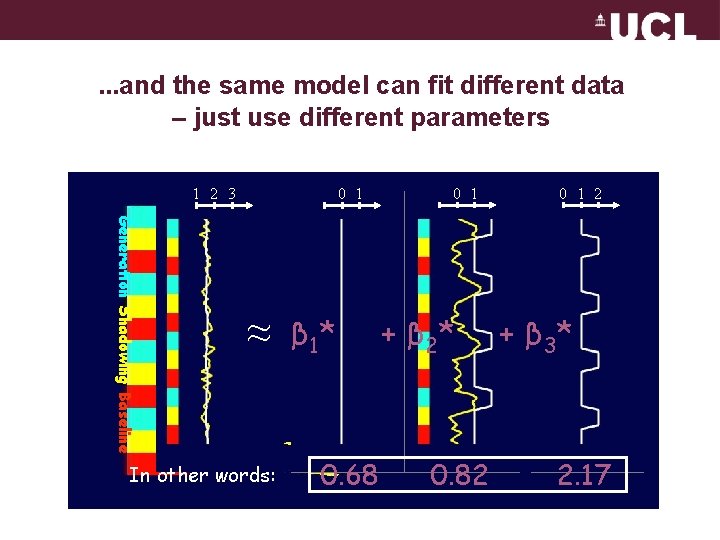
. . . and the same model can fit different data – just use different parameters 1 2 3 0 1 Generation Shadowing Baseline ≈ In other words: β 031* 0. 68 0 1 + β 21* 0. 82 0 1 2 + β 32* 2. 17

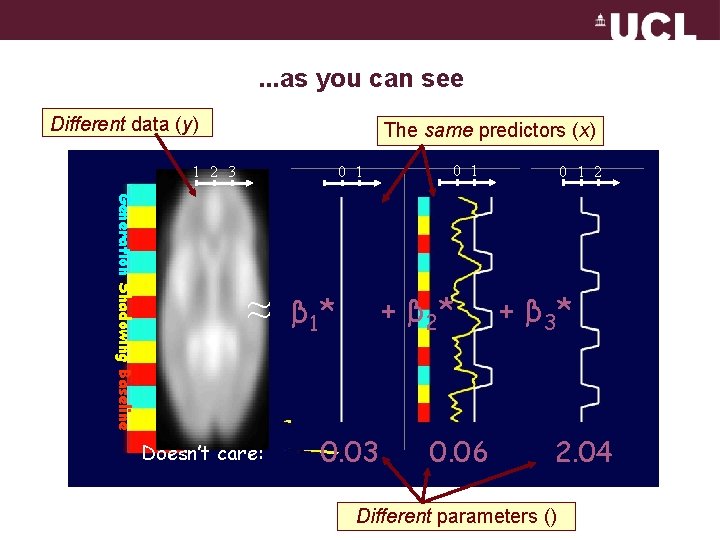
. . . as you can see Different data (y) The same predictors (x) 1 2 3 0 1 Generation Shadowing Baseline ≈ Doesn’t care: 0 1 + β 21* β 01* 0. 03 0. 06 0 1 2 + β 32* 2. 04 Different parameters ()

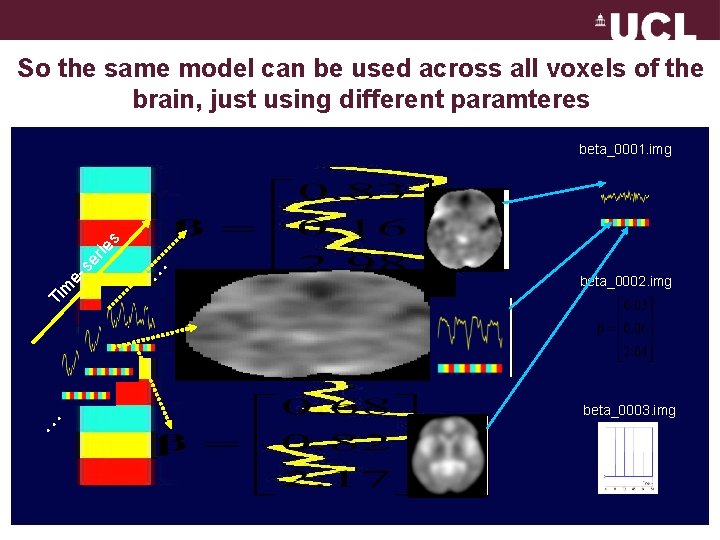
So the same model can be used across all voxels of the brain, just using different paramteres . . . Ti m . . . e- se rie s beta_0001. img beta_0002. img beta_0003. img

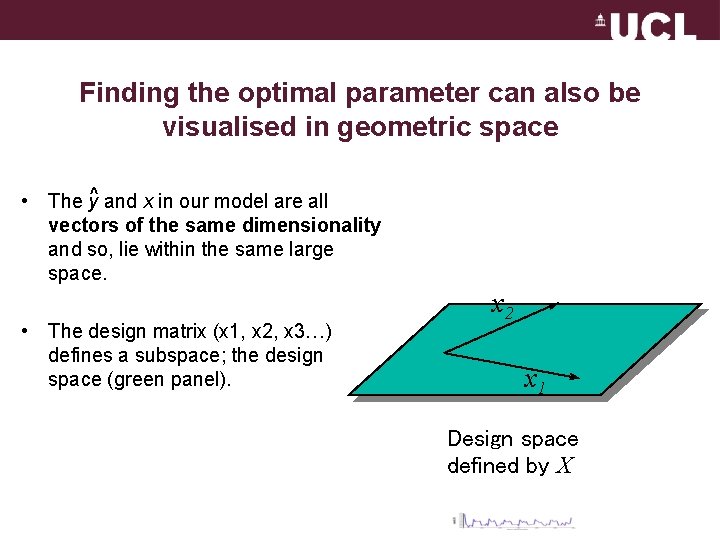
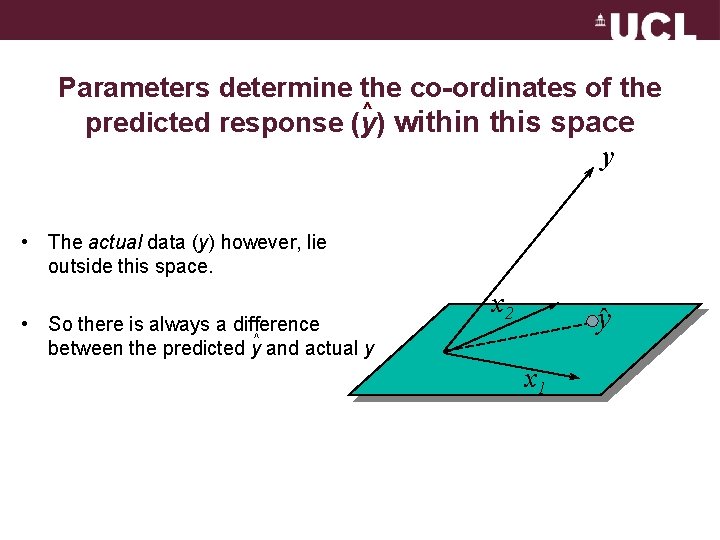
Finding the optimal parameter can also be visualised in geometric space • The y^ and x in our model are all vectors of the same dimensionality and so, lie within the same large space. • The design matrix (x 1, x 2, x 3…) defines a subspace; the design space (green panel). x 2 x 1 Design space defined by X

Parameters determine the co-ordinates of the ^ predicted response (y) within this space y • The actual data (y) however, lie outside this space. • So there is always a difference ^ between the predicted y and actual y x 2 y x 1

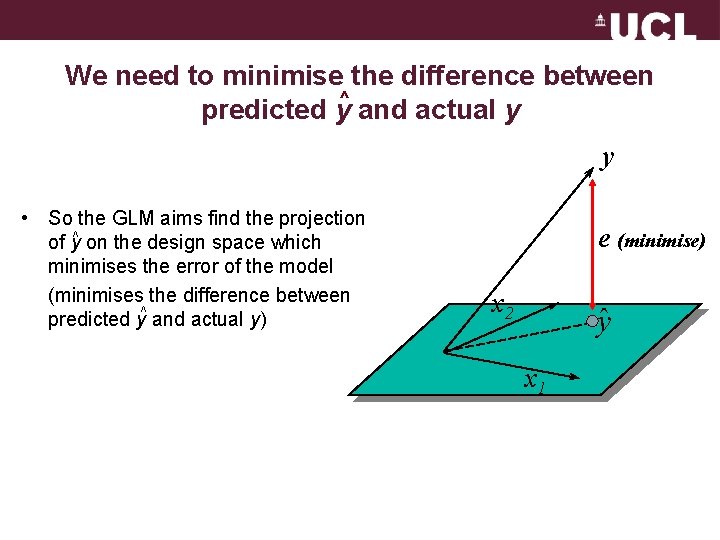
We need to minimise the difference between ^ predicted y and actual y y • So the GLM aims find the projection of y^ on the design space which minimises the error of the model (minimises the difference between ^ predicted y and actual y) e (minimise) x 2 y x 1

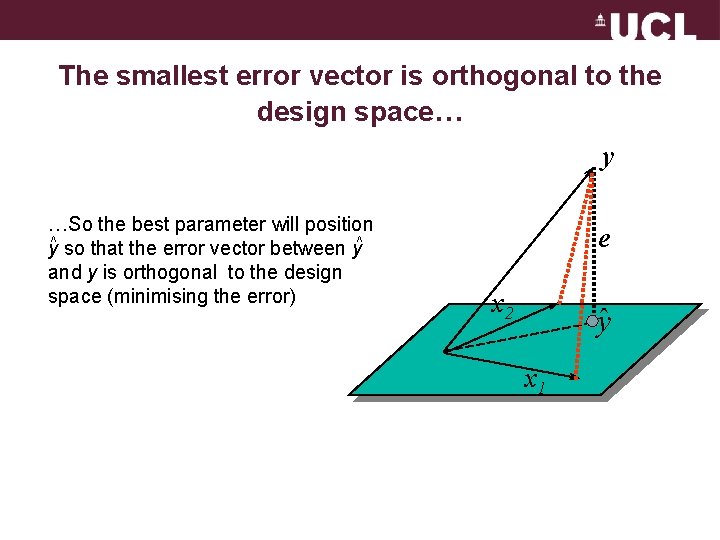
The smallest error vector is orthogonal to the design space… y …So the best parameter will position y^ so that the error vector between y^ and y is orthogonal to the design space (minimising the error) e x 2 y x 1

How do we find the parameter which produces minimal error?

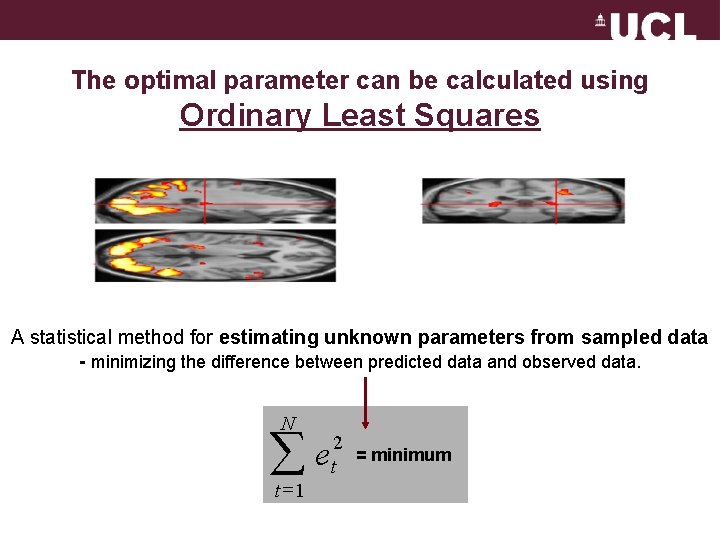
The optimal parameter can be calculated using Ordinary Least Squares A statistical method for estimating unknown parameters from sampled data - minimizing the difference between predicted data and observed data. N åe t =1 2 = minimum t

Some assumptions in GLM: Error 1. Errors are normally distributed x 2. Error is the same in each & every measurement point 3. There is no correlation between errors at different time points/data points

To re-cap…

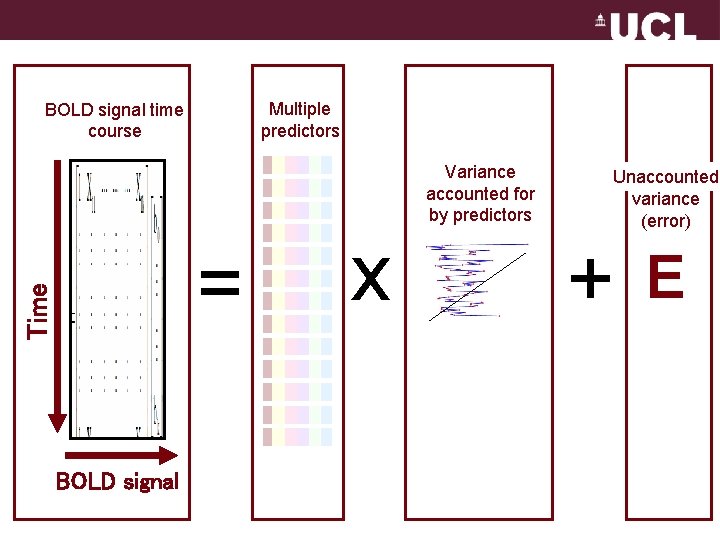
Multiple predictors BOLD signal time course Variance accounted for by predictors Time = BOLD signal x Unaccounted variance (error) + E

An f. MRI example

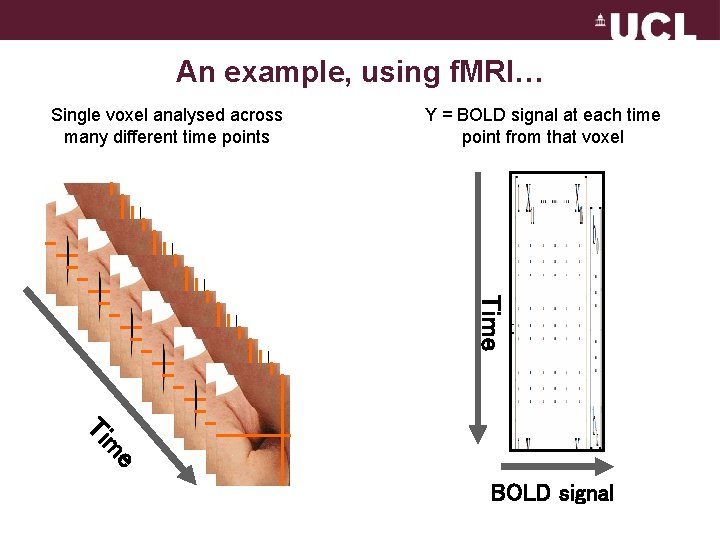
An example, using f. MRI… Single voxel analysed across many different time points Y = BOLD signal at each time point from that voxel Time e m Ti BOLD signal

A simple f. MRI experiment • One session • Passive word listening versus rest • 7 cycles of rest and listening Stimulus function Question: Is there a change in the BOLD response between listening and rest?

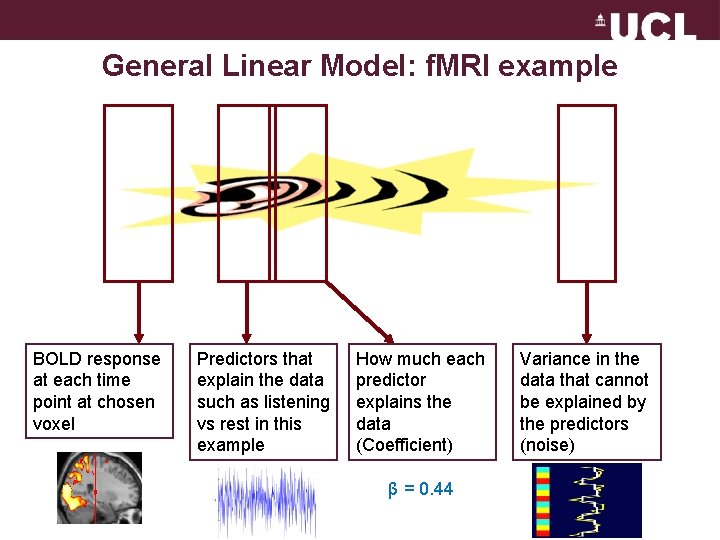
General Linear Model: f. MRI example BOLD response at each time point at chosen voxel Predictors that explain the data such as listening vs rest in this example How much each predictor explains the data (Coefficient) β = 0. 44 Variance in the data that cannot be explained by the predictors (noise)

Statistical Parametric Mapping • Null hypothesis is that your effect of interest explains none of your data. • Looking at simple listening task, how much does listening vs rest explain the BOLD signal – is it statistically significant? Statistical Inference eg. P<0. 05

Problems with this model/issues to consider. . . 1. 2. 3. 4. BOLD signal is not a simple on/off Low-frequency noise Assumptions about error may be violated Physiological confounds

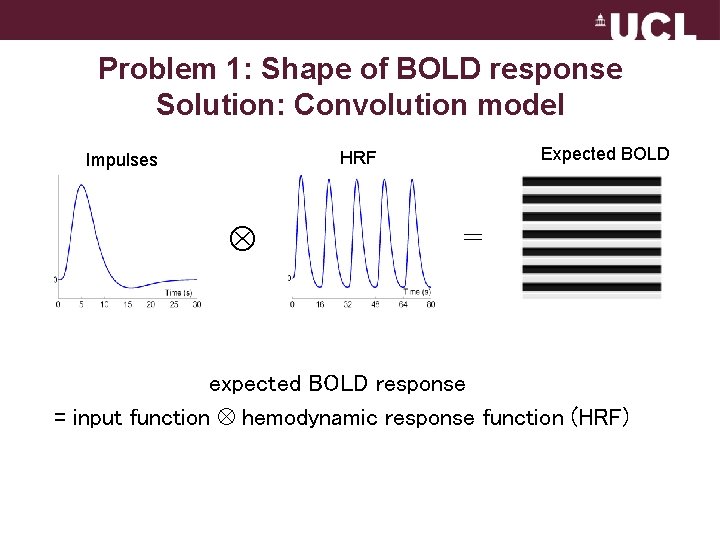
Problem 1: Shape of BOLD response Solution: Convolution model Expected BOLD HRF Impulses = expected BOLD response = input function hemodynamic response function (HRF)

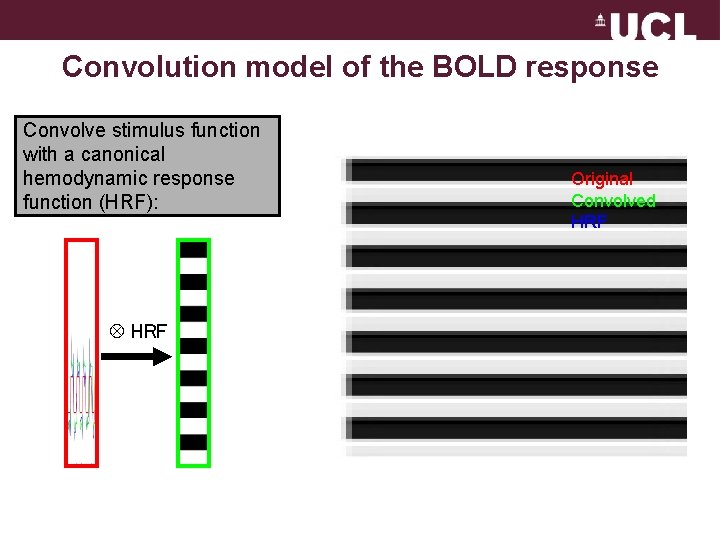
Convolution model of the BOLD response Convolve stimulus function with a canonical hemodynamic response function (HRF): HRF Original Convolved HRF

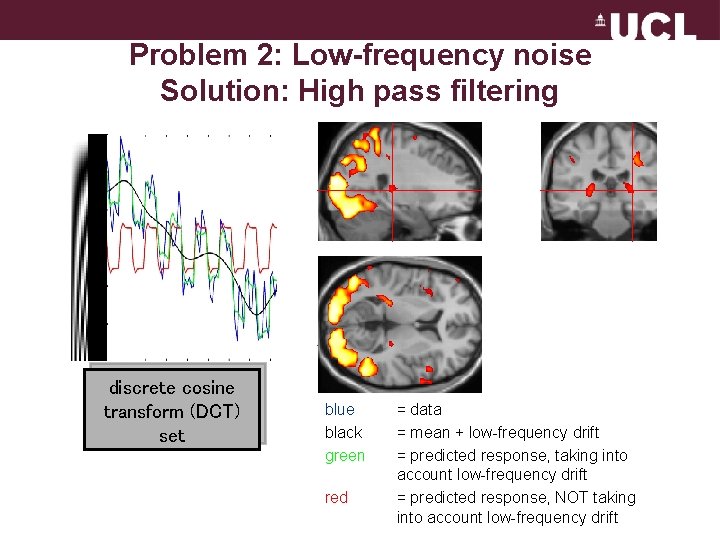
Problem 2: Low-frequency noise Solution: High pass filtering discrete cosine transform (DCT) set blue black green red = data = mean + low-frequency drift = predicted response, taking into account low-frequency drift = predicted response, NOT taking into account low-frequency drift

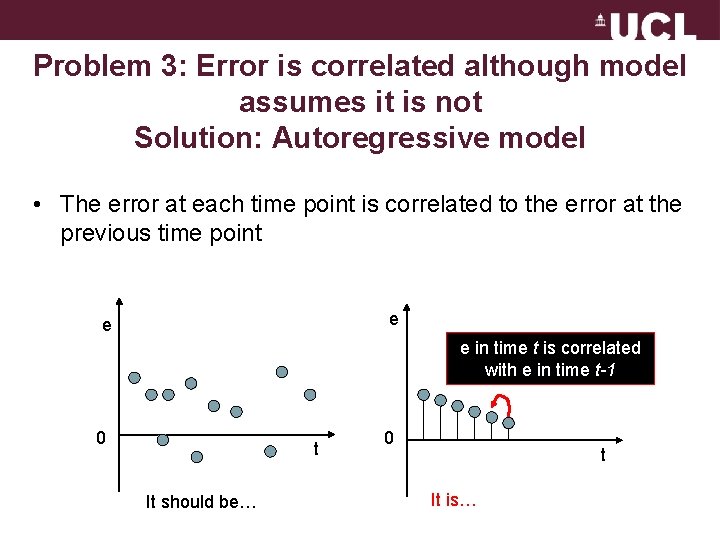
Problem 3: Error is correlated although model assumes it is not Solution: Autoregressive model • The error at each time point is correlated to the error at the previous time point e e e in time t is correlated with e in time t-1 0 t It should be… 0 t It is…

Autoregressive Model • Temporal autocorrelation: in y = Xβ + e over time Autoregressive e = ae t t-1 + ε model autocovariance function • This autocovariance function can be calculated and then the data can be analysed taking this into account, GLM is then performed again without this correlation error. This is called ‘whitening’.

Problem 4: Physiological Confounds • head movements • arterial pulsations • breathing • eye blinks (visual cortex) • adaptation affects, fatigue, changes in attention to task

To recap. . . = Response = (Predictors x Parameters. . . ) + Error

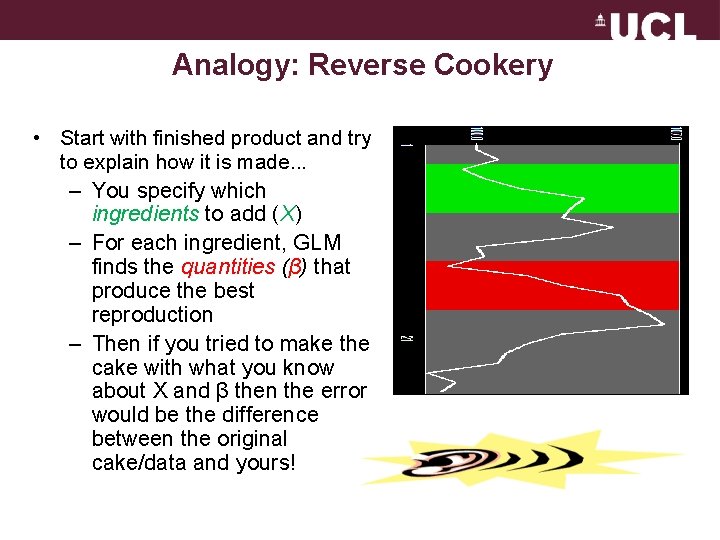
Analogy: Reverse Cookery • Start with finished product and try to explain how it is made. . . – You specify which ingredients to add (X) – For each ingredient, GLM finds the quantities (β) that produce the best reproduction – Then if you tried to make the cake with what you know about X and β then the error would be the difference between the original cake/data and yours!

Thanks to. . . • Previous years Mf. D slides (2003 -2009) • Guillaume Flandin (our expert) • Slides from previous SPM courses – http: //www. fil. ion. ucl. ac. uk/spm/course/ • Suz and Christian