Spiking models 1 Neuronal codes Spiking models Hodgkin

Spiking models 1

Neuronal codes Spiking models: • Hodgkin Huxley Model (brief repetition) • Reduction of the HH-Model to two dimensions (general) • Fitz. Hugh-Nagumo Model • Integrate and Fire Model 2

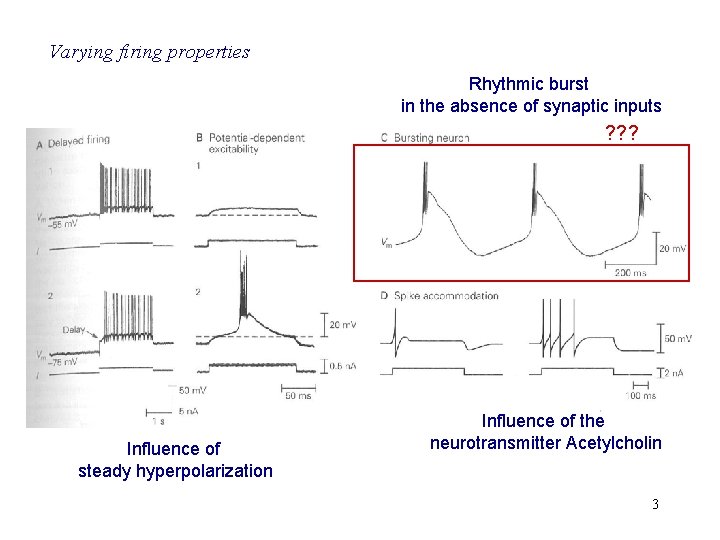
Varying firing properties Rhythmic burst in the absence of synaptic inputs ? ? ? Influence of steady hyperpolarization Influence of the neurotransmitter Acetylcholin 3

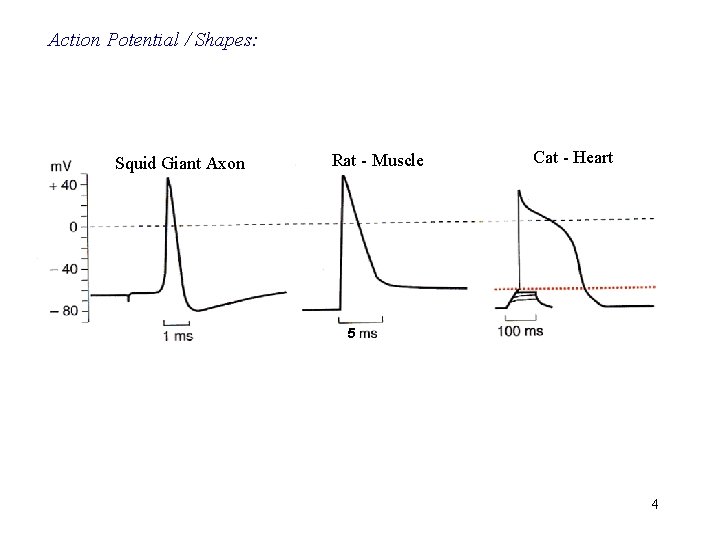
Action Potential / Shapes: Squid Giant Axon Rat - Muscle Cat - Heart 5 4

Your neurons surely don‘t like this guy! 5

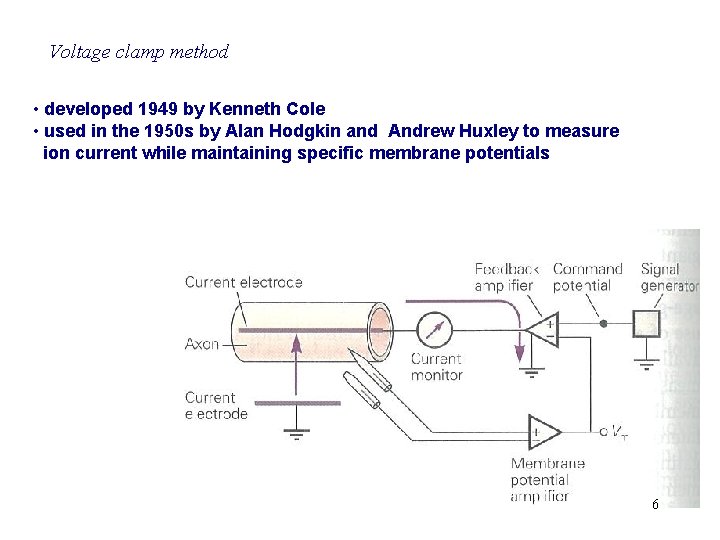
Voltage clamp method • developed 1949 by Kenneth Cole • used in the 1950 s by Alan Hodgkin and Andrew Huxley to measure ion current while maintaining specific membrane potentials 6

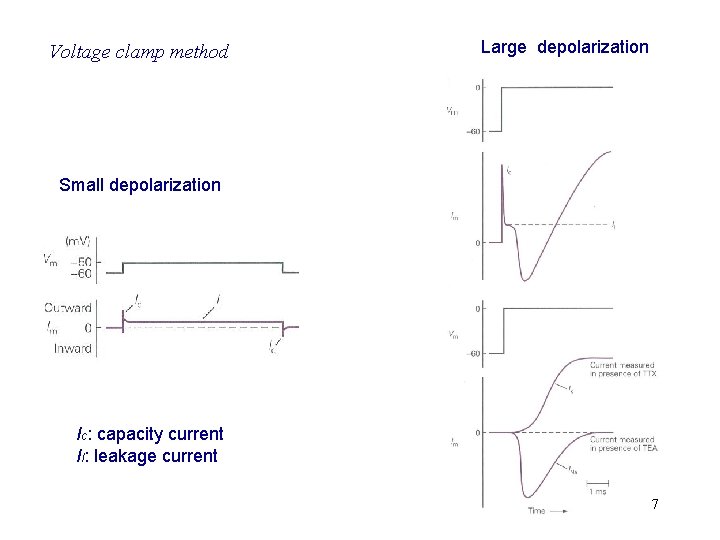
Voltage clamp method Large depolarization Small depolarization Ic: capacity current Il: leakage current 7

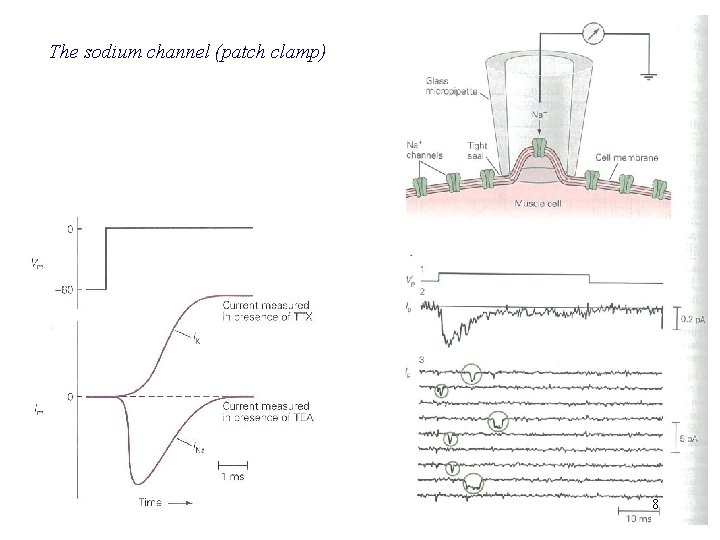
The sodium channel (patch clamp) 8

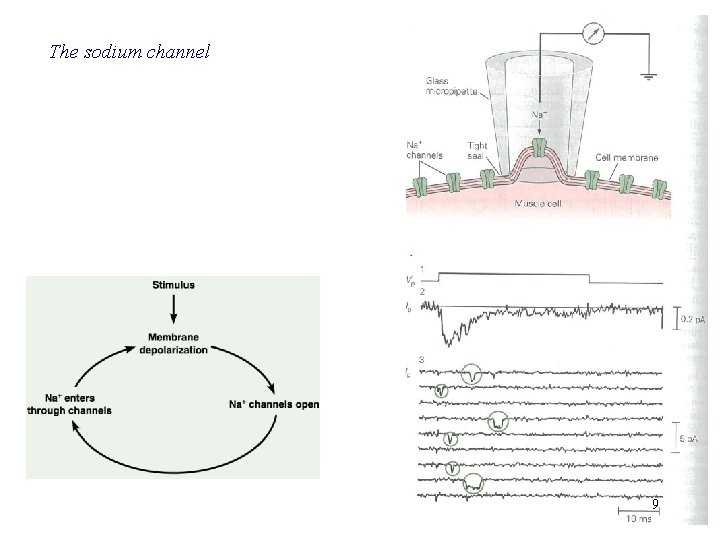
The sodium channel 9

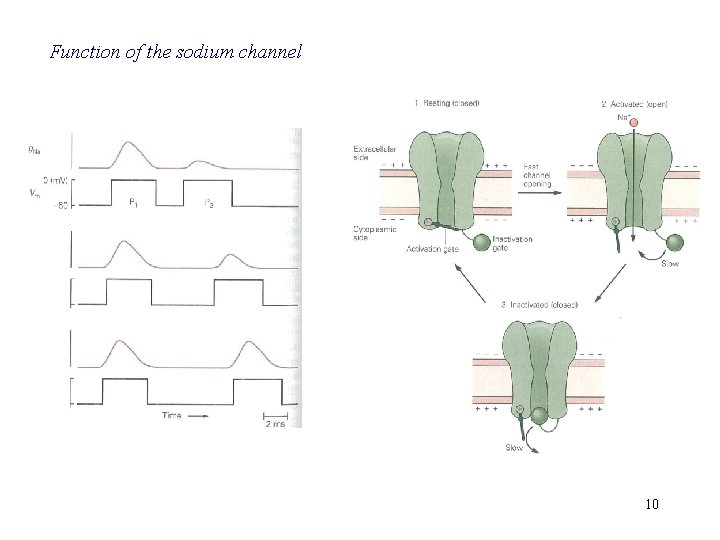
Function of the sodium channel 10

Hodgkin and Huxley 11

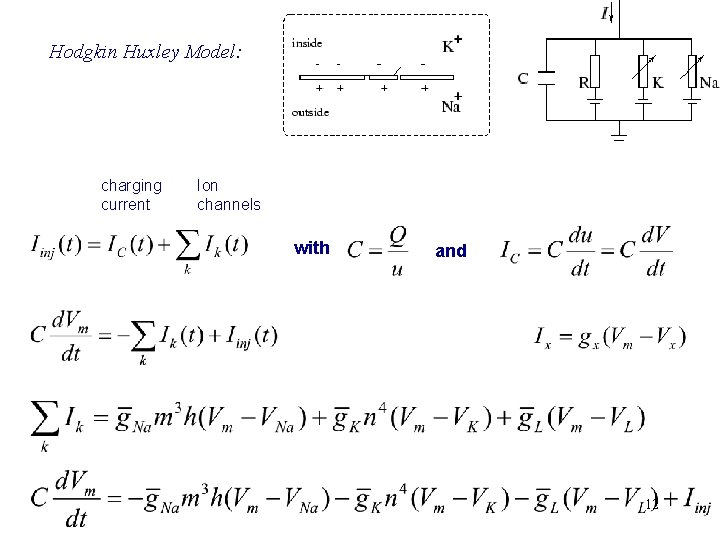
Hodgkin Huxley Model: charging current Ion channels with and 12

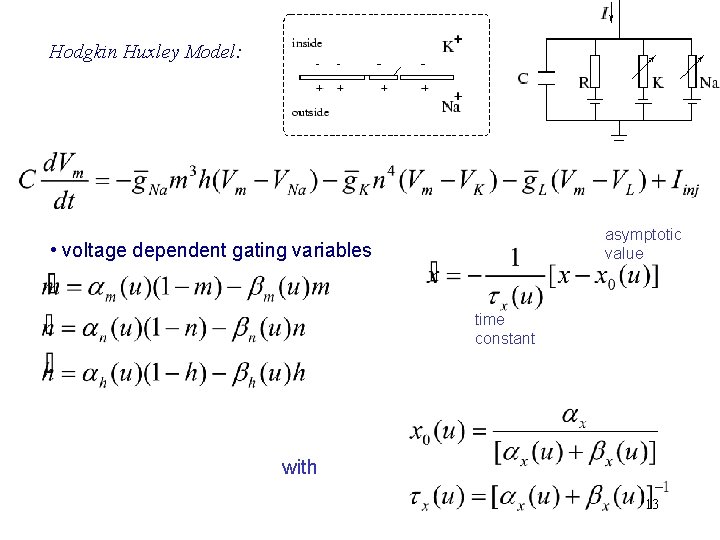
Hodgkin Huxley Model: asymptotic value • voltage dependent gating variables time constant with 13

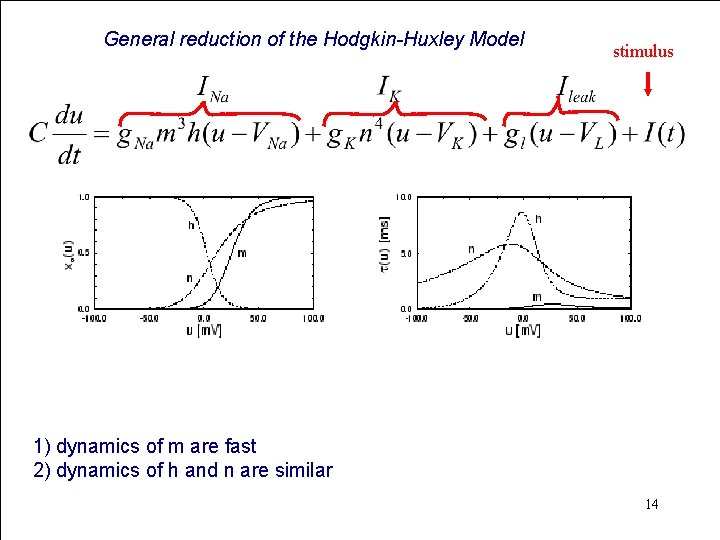
General reduction of the Hodgkin-Huxley Model stimulus 1) dynamics of m are fast 2) dynamics of h and n are similar 14

General Reduction of the Hodgkin-Huxley Model: 2 dimensional Neuron Models stimulus 15

Fitz. Hugh-Nagumo Model u: membran potential w: recovery variable I: stimulus 16

Introduction to dynamical systems Simple Example: Harmonic Oscillator 17

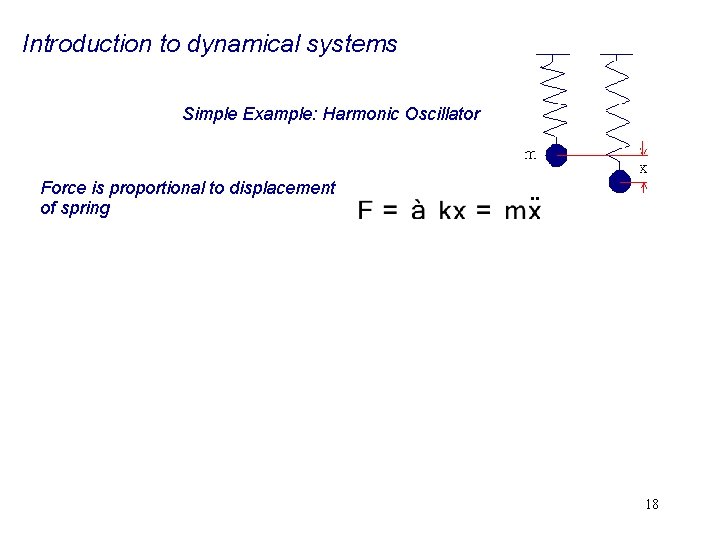
Introduction to dynamical systems Simple Example: Harmonic Oscillator Force is proportional to displacement of spring . . 18

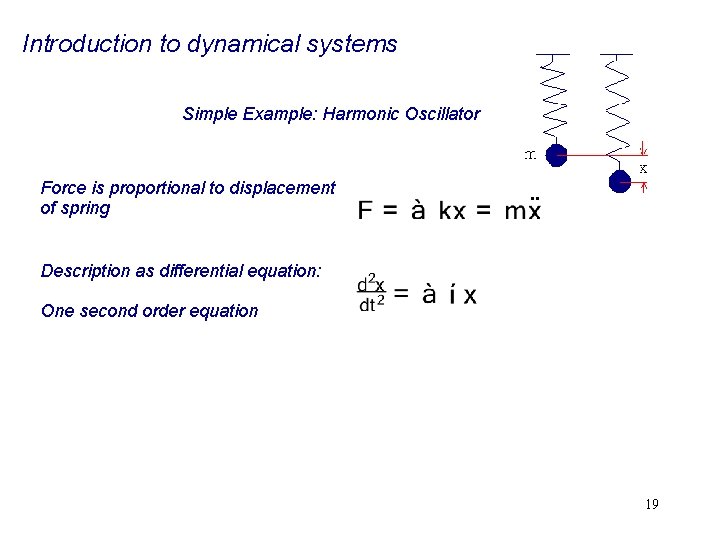
Introduction to dynamical systems Simple Example: Harmonic Oscillator Force is proportional to displacement of spring . . Description as differential equation: One second order equation 19

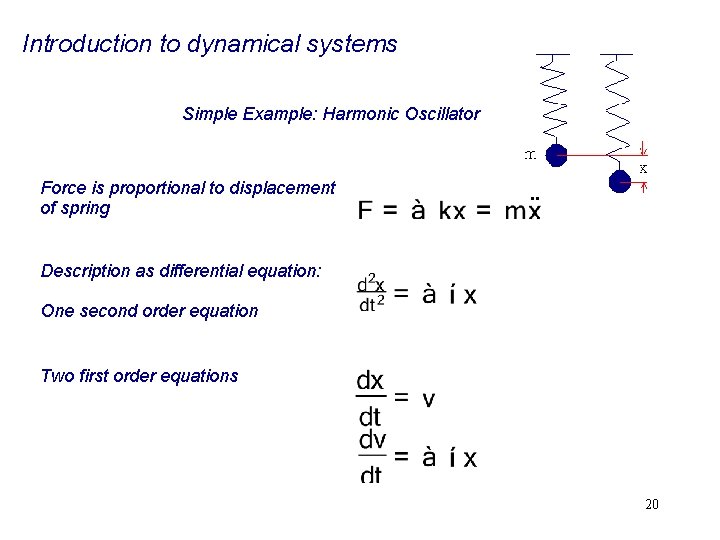
Introduction to dynamical systems Simple Example: Harmonic Oscillator Force is proportional to displacement of spring . . Description as differential equation: One second order equation Two first order equations 20

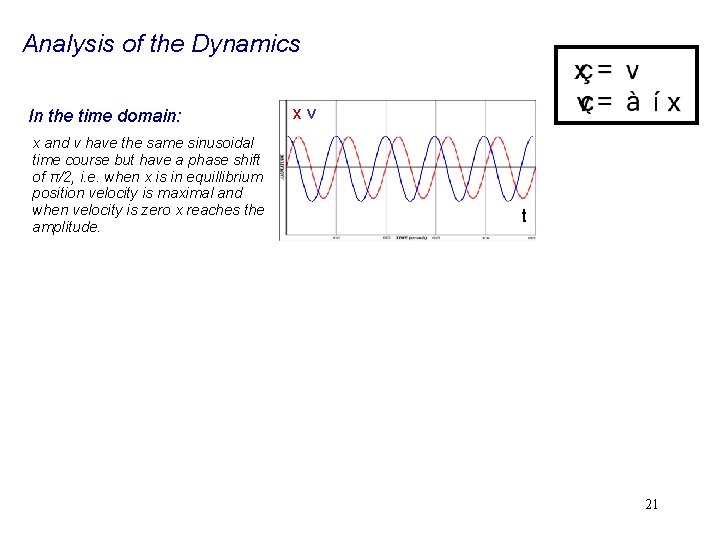
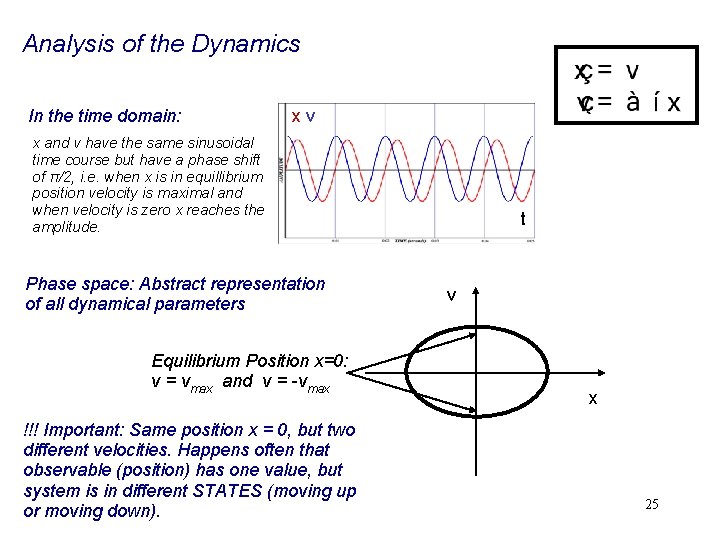
Analysis of the Dynamics In the time domain: x and v have the same sinusoidal time course but have a phase shift of π/2, i. e. when x is in equillibrium position velocity is maximal and when velocity is zero x reaches the amplitude. xv t 21

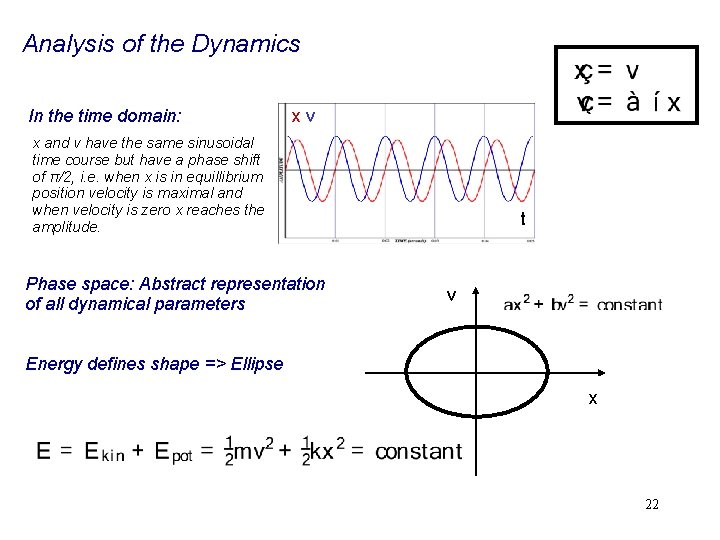
Analysis of the Dynamics In the time domain: xv x and v have the same sinusoidal time course but have a phase shift of π/2, i. e. when x is in equillibrium position velocity is maximal and when velocity is zero x reaches the amplitude. Phase space: Abstract representation of all dynamical parameters t v Energy defines shape => Ellipse x 22

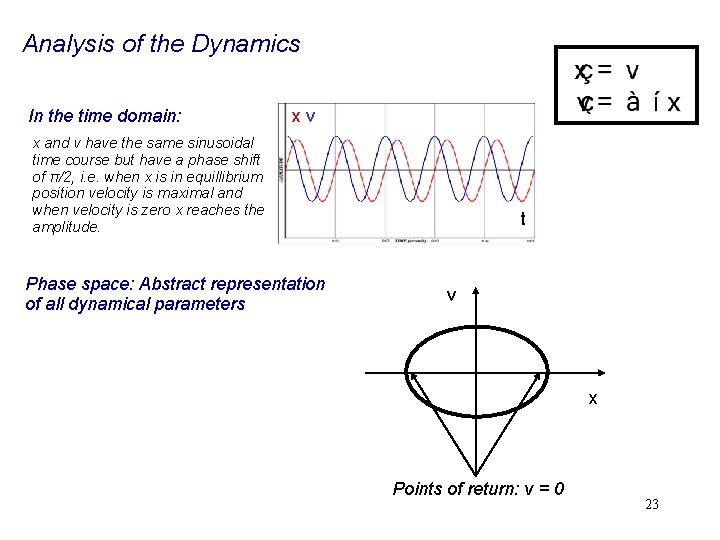
Analysis of the Dynamics In the time domain: xv x and v have the same sinusoidal time course but have a phase shift of π/2, i. e. when x is in equillibrium position velocity is maximal and when velocity is zero x reaches the amplitude. Phase space: Abstract representation of all dynamical parameters t v x Points of return: v = 0 23

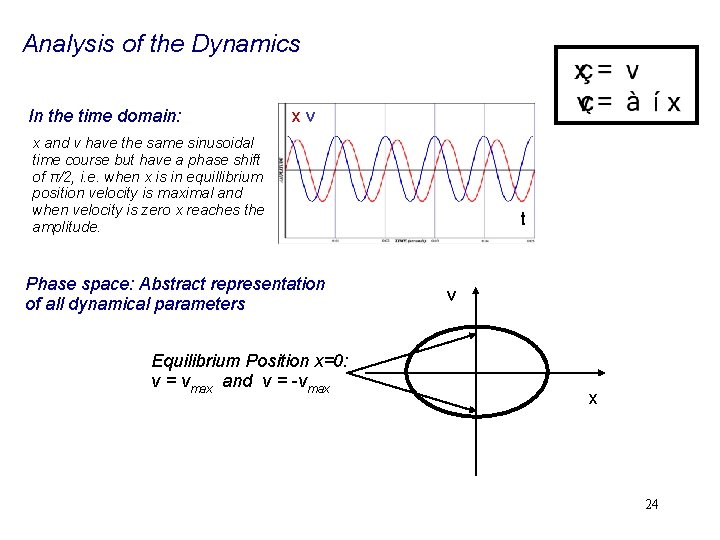
Analysis of the Dynamics In the time domain: xv x and v have the same sinusoidal time course but have a phase shift of π/2, i. e. when x is in equillibrium position velocity is maximal and when velocity is zero x reaches the amplitude. Phase space: Abstract representation of all dynamical parameters Equilibrium Position x=0: v = vmax and v = -vmax t v x 24

Analysis of the Dynamics In the time domain: xv x and v have the same sinusoidal time course but have a phase shift of π/2, i. e. when x is in equillibrium position velocity is maximal and when velocity is zero x reaches the amplitude. Phase space: Abstract representation of all dynamical parameters Equilibrium Position x=0: v = vmax and v = -vmax !!! Important: Same position x = 0, but two different velocities. Happens often that observable (position) has one value, but system is in different STATES (moving up or moving down). t v x 25

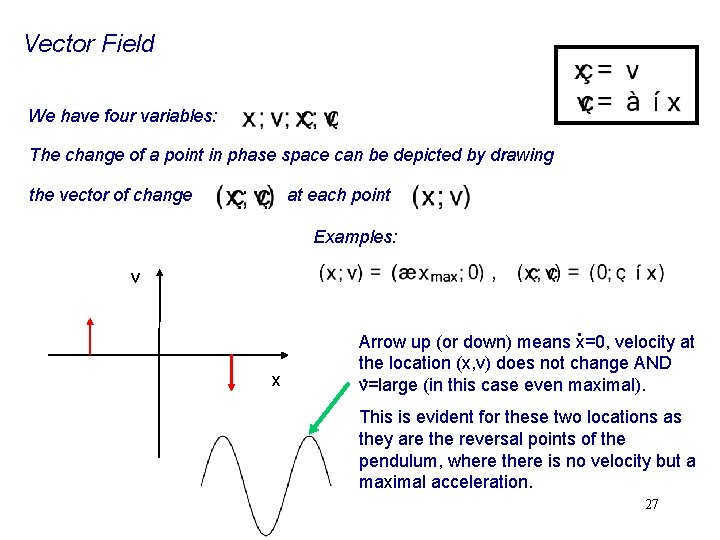
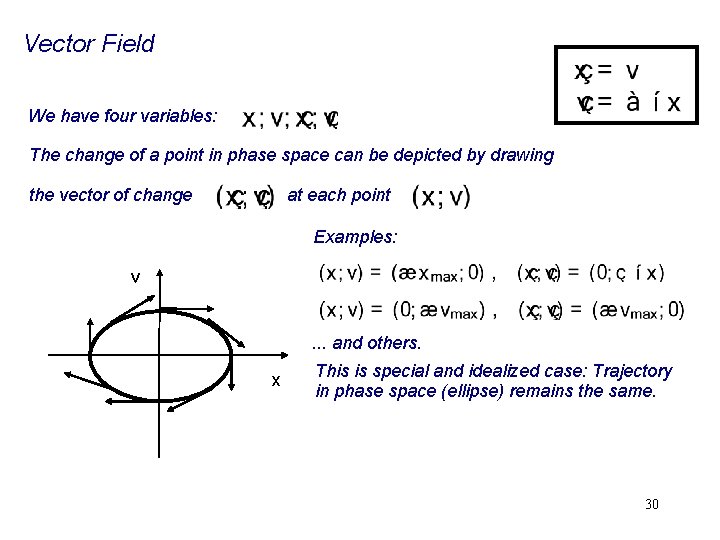
Vector Field We have four variables: The change of a point in phase space can be depicted by drawing the vector of change at each point 26

Vector Field We have four variables: The change of a point in phase space can be depicted by drawing the vector of change at each point Examples: v x . Arrow up (or down) means x=0, velocity at the location (x, v) does not change AND. v=large (in this case even maximal). This is evident for these two locations as they are the reversal points of the pendulum, where there is no velocity but a maximal acceleration. 27

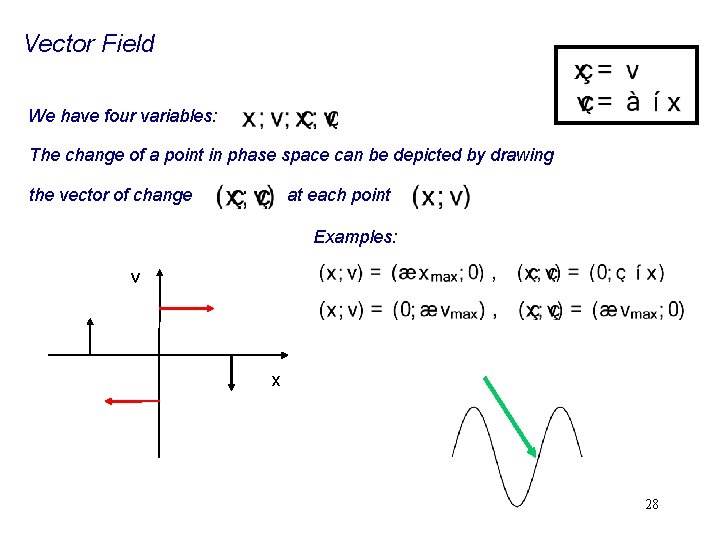
Vector Field We have four variables: The change of a point in phase space can be depicted by drawing the vector of change at each point Examples: v x 28

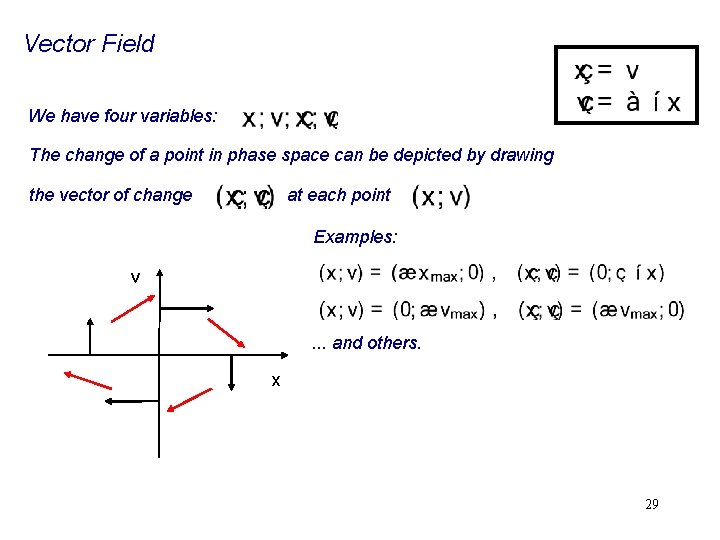
Vector Field We have four variables: The change of a point in phase space can be depicted by drawing the vector of change at each point Examples: v . . . and others. x 29

Vector Field We have four variables: The change of a point in phase space can be depicted by drawing the vector of change at each point Examples: v . . . and others. x This is special and idealized case: Trajectory in phase space (ellipse) remains the same. 30

Vector Field We have four variables: The change of a point in phase space can be depicted by drawing the vector of change at each point Examples: v . . . and others. x This is special and idealized case: Trajectory in phase space (ellipse) remains the same. It depends only on the initial conditions (how far we strain the spring in the beginning). 31

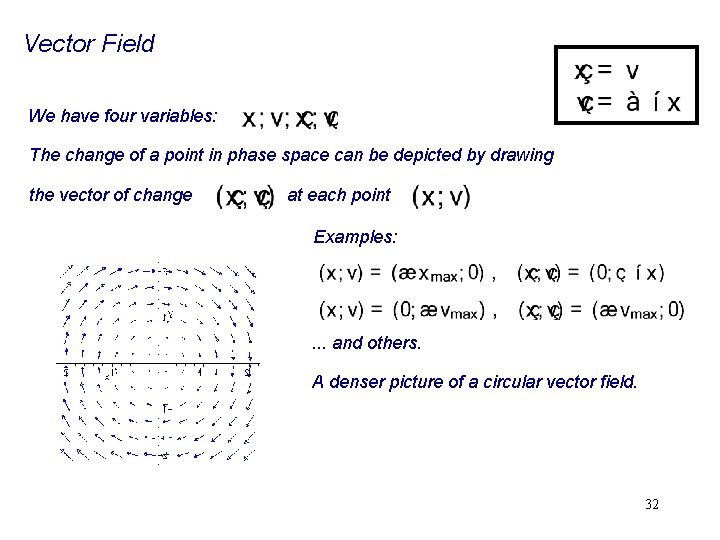
Vector Field We have four variables: The change of a point in phase space can be depicted by drawing the vector of change at each point Examples: . . . and others. A denser picture of a circular vector field. 32

Vector Field We have four variables: The change of a point in phase space can be depicted by drawing the vector of change at each point Examples: . . . and others. Here is an example for an oscillator with damping: The phase space trajectory always returns to the resting position and 33

Vector Field We have four variables: The change of a point in phase space can be depicted by drawing the vector of change at each point Examples: . . . and others. And vector fields can be really crazy. . . 34

Fixed Points For analysis of dynamical systems there are points of special interest where the system or a particular variable does not change, i. e. the vector 35

Fixed Points For analysis of dynamical systems there are points of special interest where the system or a particular variable does not change, i. e. the vector Look at our simple example: For which values (x, v) is the upper equation true and what does this solution mean? 36

Fixed Points For analysis of dynamical systems there are points of special interest where the system or a particular variable does not change, i. e. the vector Look at our simple example: For which values (x, v) is the upper equation true and what does this solution mean? Only for one single point , the FIXED POINT 37

Fixed Points For analysis of dynamical systems there are points of special interest where the system or a particular variable does not change, i. e. the vector Look at our simple example: For which values (x, v) is the upper equation true and what does this solution mean? Only for one single point , the FIXED POINT In the simplest case: a resting pendulum! This is also true for the damped oscillator, but there the fixed point is also an ATTRACTOR, i. e. no matter where we start in phase space we will always end up at the resting position. No surprise! 38

Fixed Points II and Other Stuff Consider a more general case: Still interesting where the system doesn't change: 39

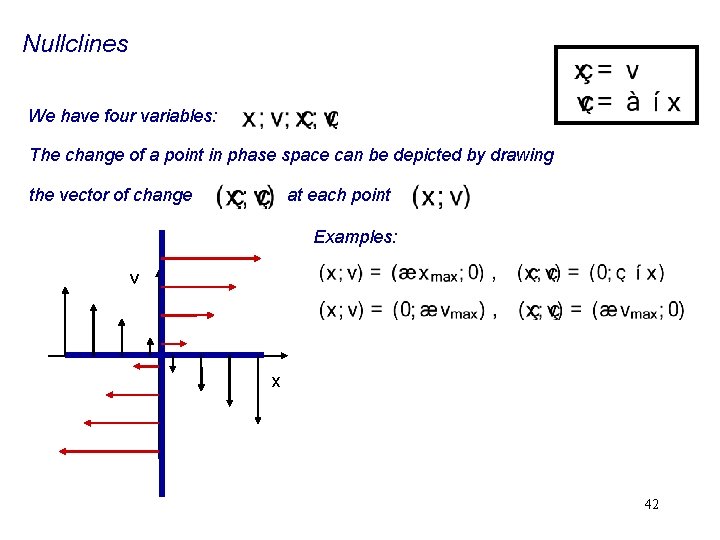
Fixed Points II and Other Stuff Consider a more general case: Still interesting where the system doesn't change: The geometric functions that we get from these equations are called NULLCLINES. They signify where the vectors of the vector fields are only horizontal or vertical. At the intersection of the nullclines we find fixed points. 40

Fixed Points II and Other Stuff Consider a more general case: Still interesting where the system doesn't change: The geometric functions that we get from these equations are called NULLCLINES. They signify where the vectors of the vector fields are only horizontal or vertical. At the intersection of the nullclines we find fixed points. For the simple spring example we find the trivial nullclines: They intersect at which is the fixed point. 41

Nullclines We have four variables: The change of a point in phase space can be depicted by drawing the vector of change at each point Examples: v x 42

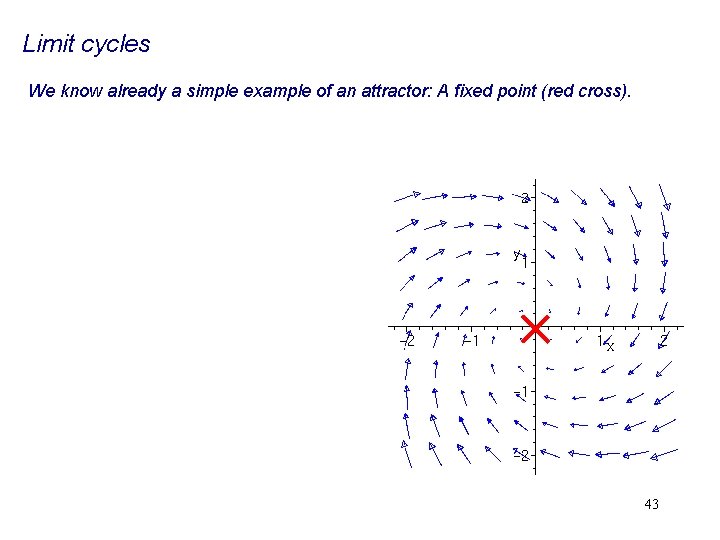
Limit cycles We know already a simple example of an attractor: A fixed point (red cross). 43

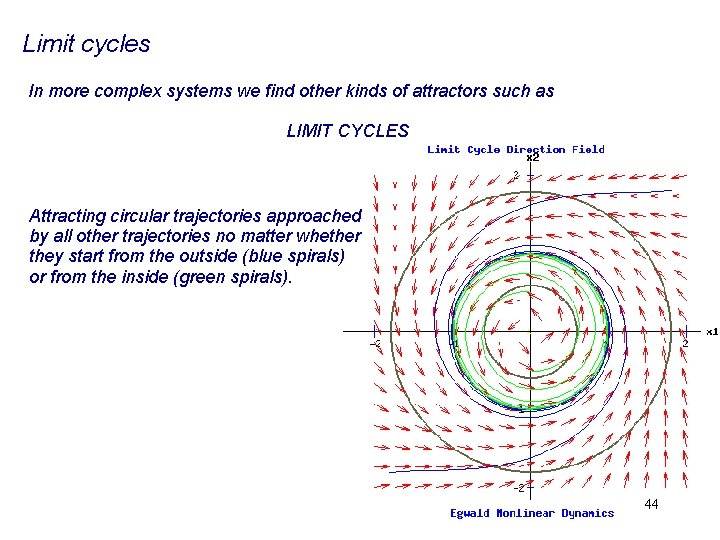
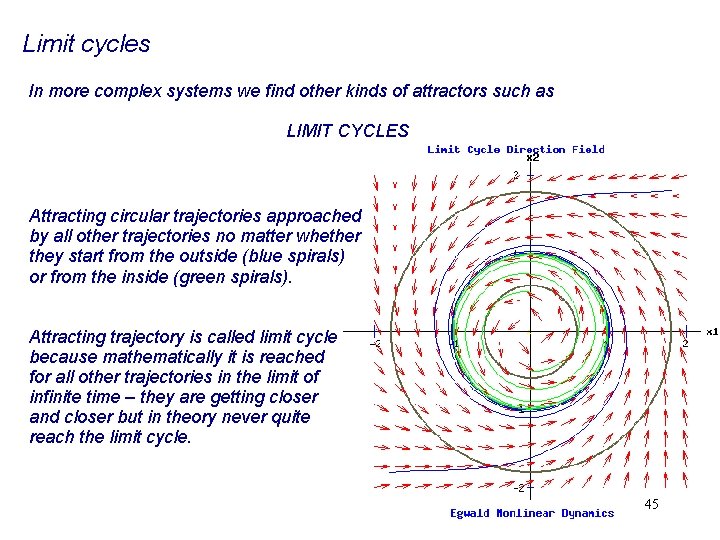
Limit cycles In more complex systems we find other kinds of attractors such as LIMIT CYCLES Attracting circular trajectories approached by all other trajectories no matter whether they start from the outside (blue spirals) or from the inside (green spirals). 44

Limit cycles In more complex systems we find other kinds of attractors such as LIMIT CYCLES Attracting circular trajectories approached by all other trajectories no matter whether they start from the outside (blue spirals) or from the inside (green spirals). Attracting trajectory is called limit cycle because mathematically it is reached for all other trajectories in the limit of infinite time – they are getting closer and closer but in theory never quite reach the limit cycle. 45

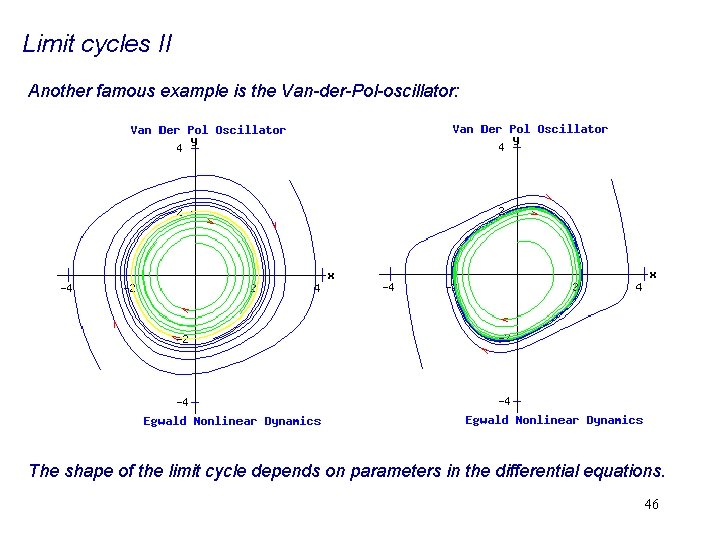
Limit cycles II Another famous example is the Van-der-Pol-oscillator: The shape of the limit cycle depends on parameters in the differential equations. 46

General Reduction of the Hodgkin-Huxley Model: 2 dimensional Neuron Models stimulus 47

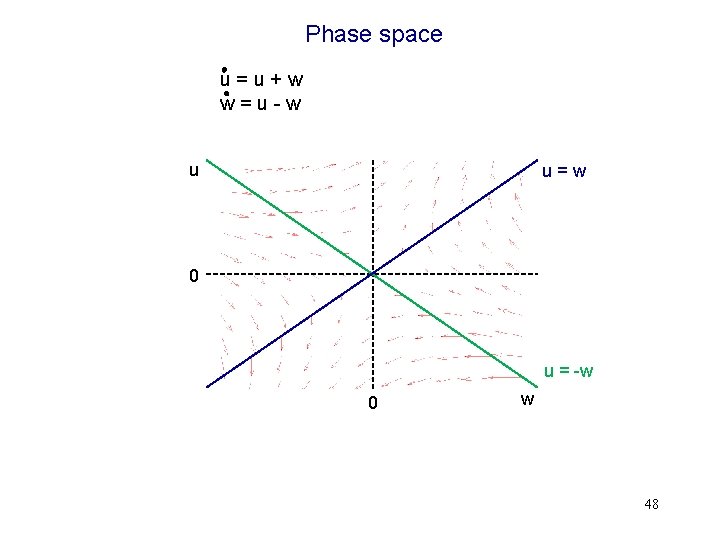
Phase space u=u+w w=u-w u u=w 0 u = -w 0 w 48

Hodgkin Huxley Model: • voltage dependent gating variables Assumputions that lead to the FH-Model m -> 0 h = const. 49

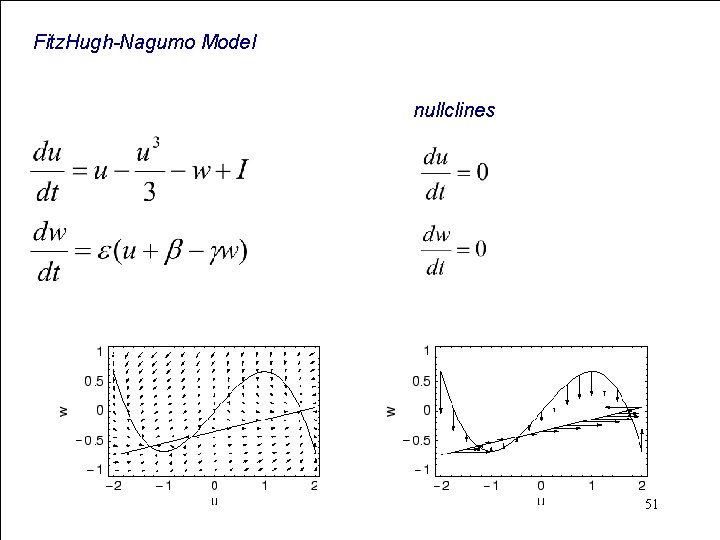
Fitz. Hugh-Nagumo Model u: membran potential w: recovery variable I: stimulus 50

Fitz. Hugh-Nagumo Model nullclines 51

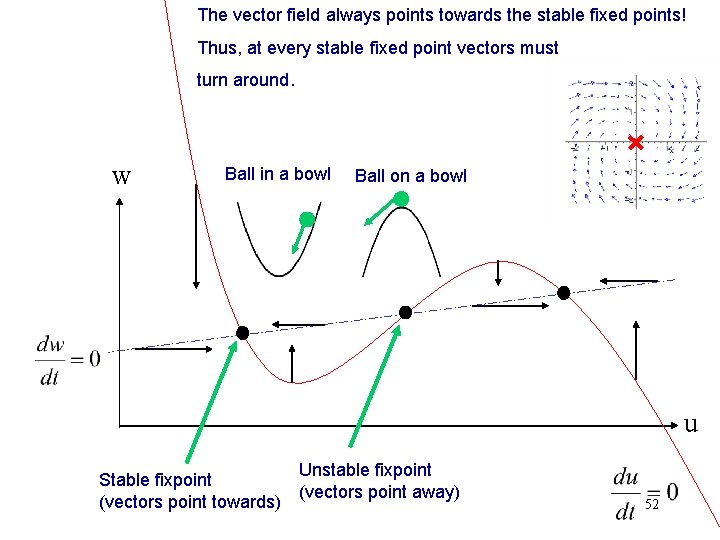
The vector field always points towards the stable fixed points! Thus, at every stable fixed point vectors must turn around. w Ball in a bowl Ball on a bowl u Unstable fixpoint Stable fixpoint (vectors point away) (vectors point towards) 52

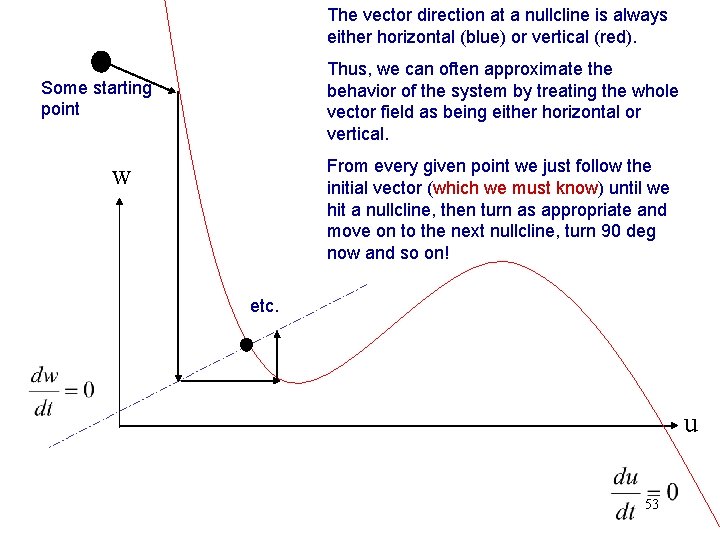
The vector direction at a nullcline is always either horizontal (blue) or vertical (red). Thus, we can often approximate the behavior of the system by treating the whole vector field as being either horizontal or vertical. Some starting point From every given point we just follow the initial vector (which we must know) until we hit a nullcline, then turn as appropriate and move on to the next nullcline, turn 90 deg now and so on! w etc. u 53

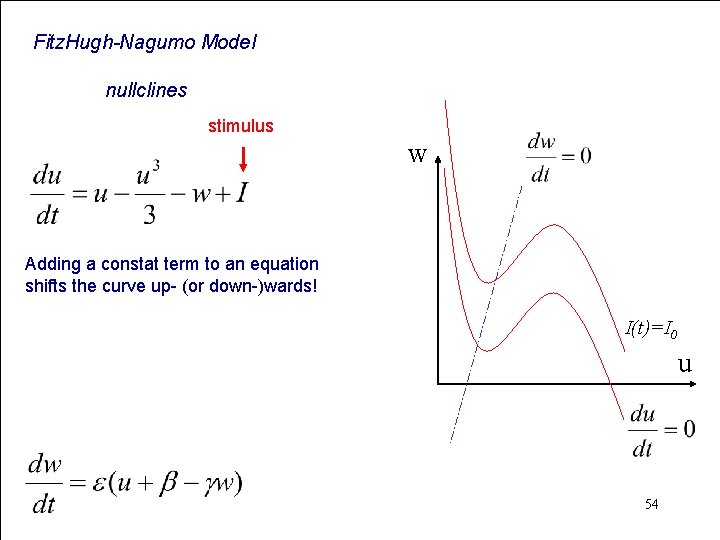
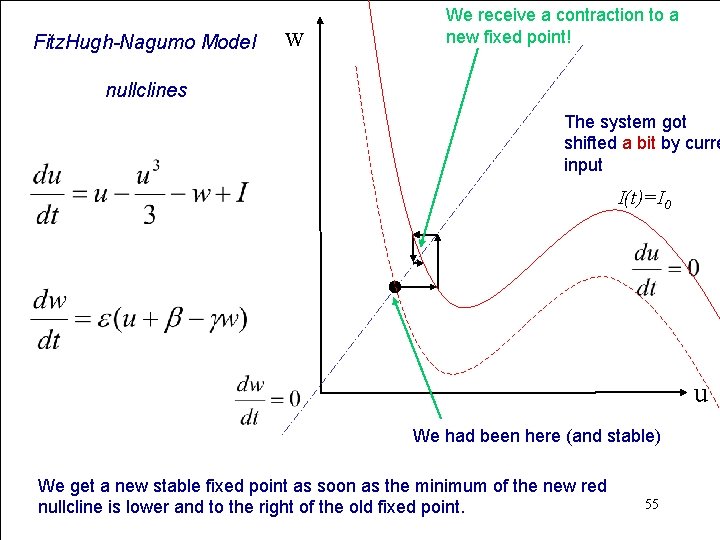
Fitz. Hugh-Nagumo Model nullclines stimulus w Adding a constat term to an equation shifts the curve up- (or down-)wards! I(t)=I 0 u 54

Fitz. Hugh-Nagumo Model w We receive a contraction to a new fixed point! nullclines The system got shifted a bit by curre input I(t)=I 0 u We had been here (and stable) We get a new stable fixed point as soon as the minimum of the new red nullcline is lower and to the right of the old fixed point. 55

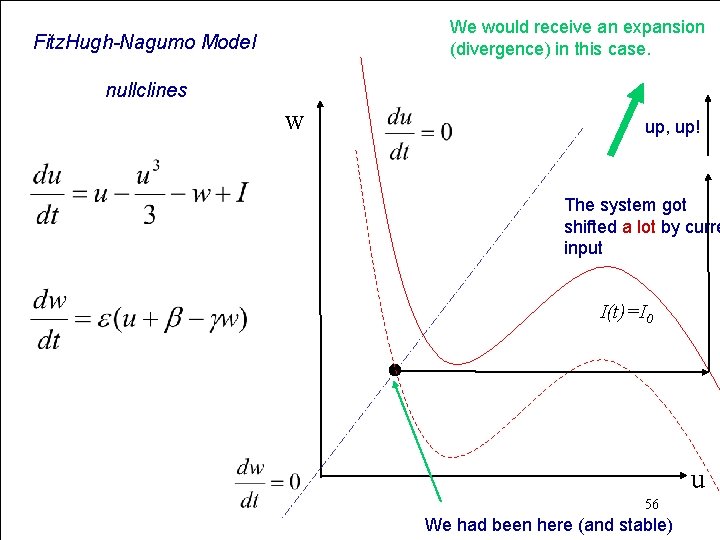
We would receive an expansion (divergence) in this case. Fitz. Hugh-Nagumo Model nullclines w up, up! The system got shifted a lot by curre input I(t)=I 0 u 56 We had been here (and stable)

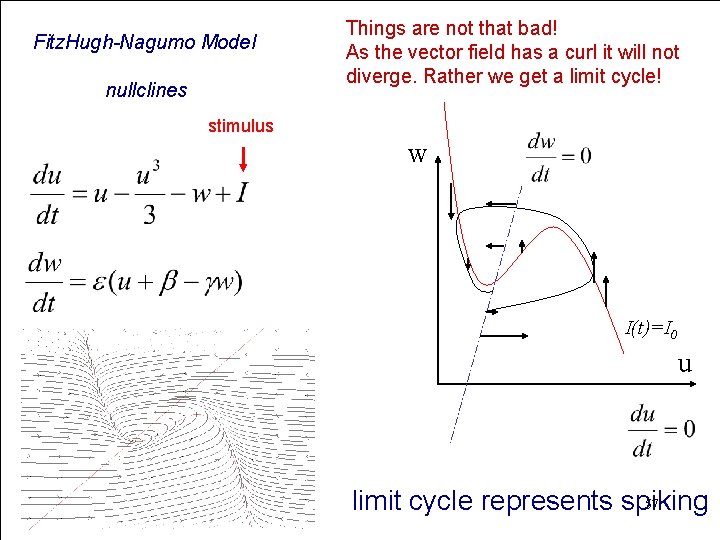
Fitz. Hugh-Nagumo Model nullclines Things are not that bad! As the vector field has a curl it will not diverge. Rather we get a limit cycle! stimulus w I(t)=I 0 u 57 limit cycle represents spiking

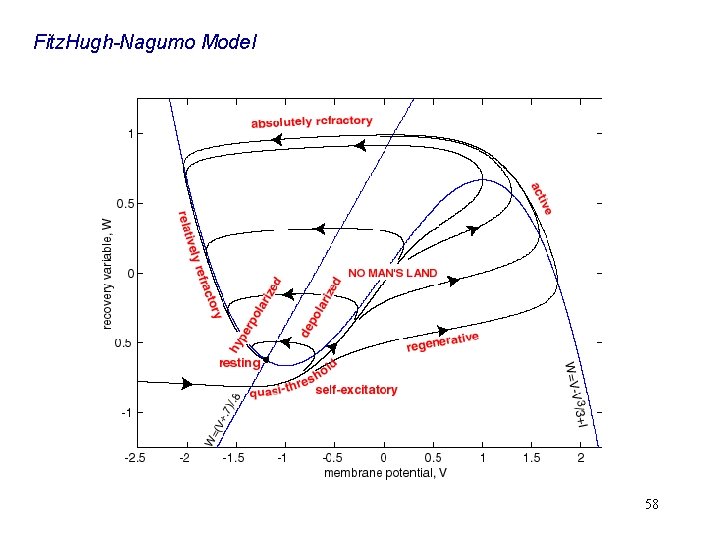
Fitz. Hugh-Nagumo Model 58

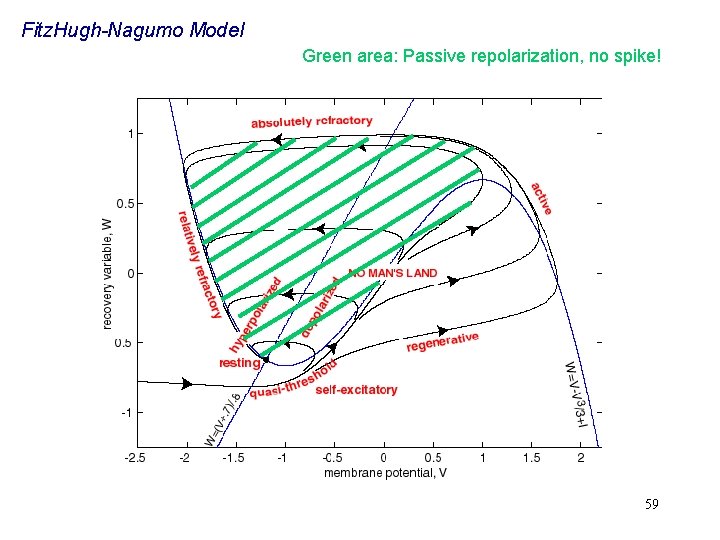
Fitz. Hugh-Nagumo Model Green area: Passive repolarization, no spike! 59

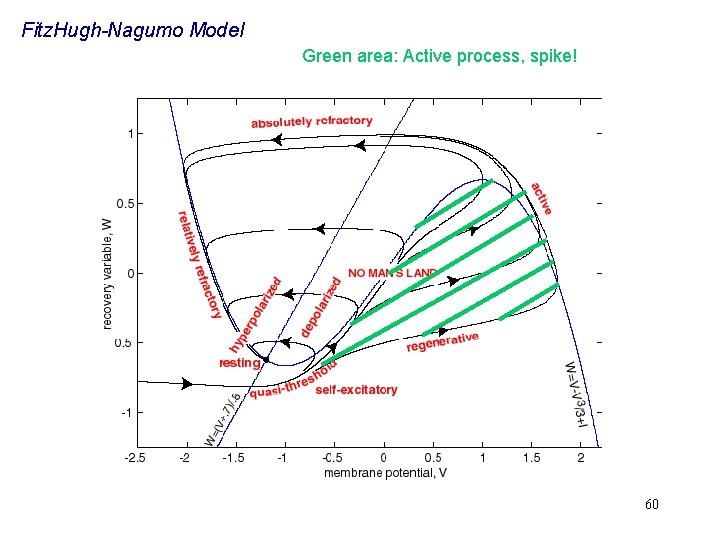
Fitz. Hugh-Nagumo Model Green area: Active process, spike! 60

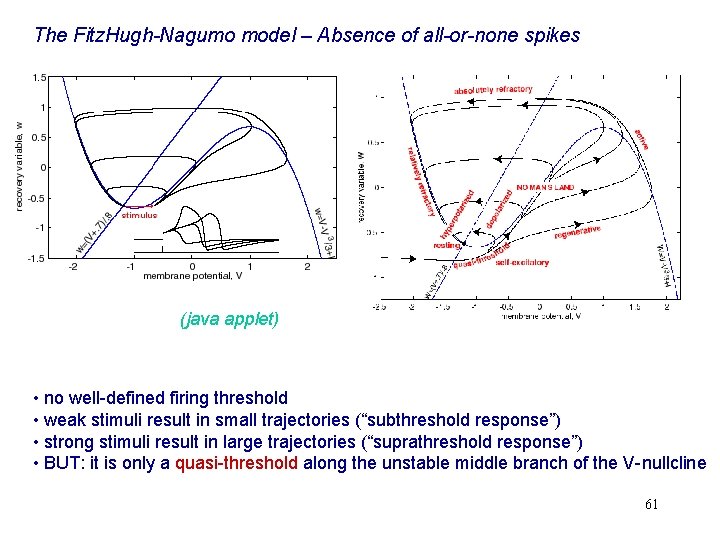
The Fitz. Hugh-Nagumo model – Absence of all-or-none spikes (java applet) • no well-defined firing threshold • weak stimuli result in small trajectories (“subthreshold response”) • strong stimuli result in large trajectories (“suprathreshold response”) • BUT: it is only a quasi-threshold along the unstable middle branch of the V-nullcline 61

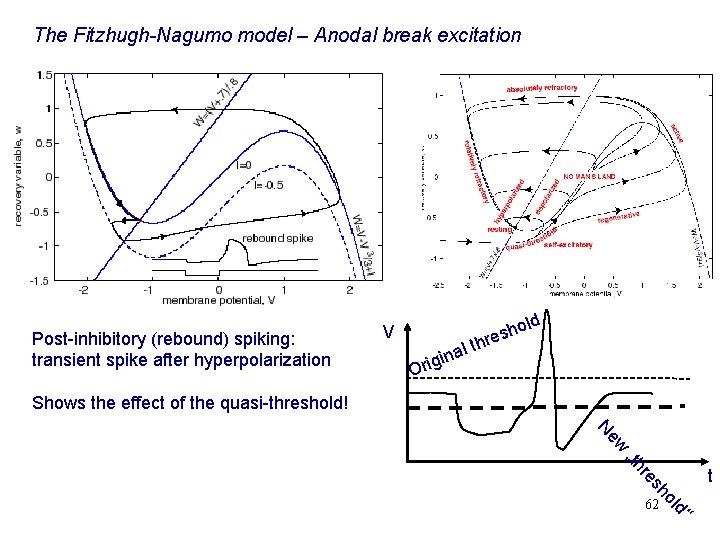
The Fitzhugh-Nagumo model – Anodal break excitation Post-inhibitory (rebound) spiking: transient spike after hyperpolarization old h s re al th V in g i r O Shows the effect of the quasi-threshold! Ne w re „th ol sh d“ 62 t

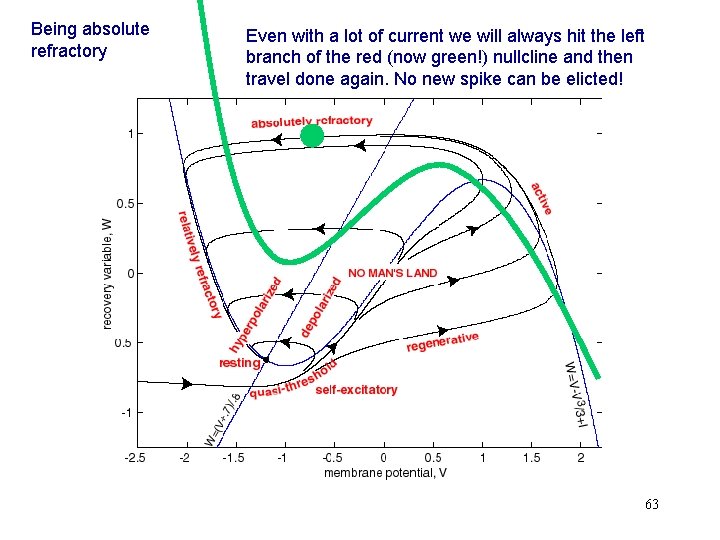
Being absolute refractory Even with a lot of current we will always hit the left branch of the red (now green!) nullcline and then travel done again. No new spike can be elicted! 63

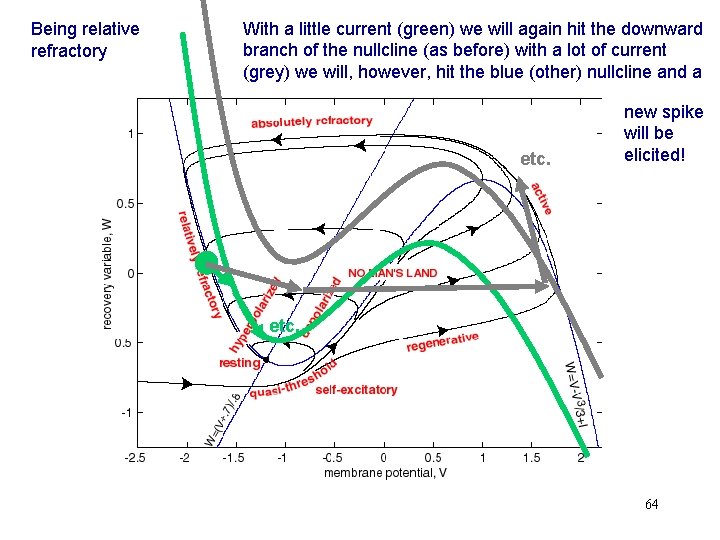
Being relative refractory With a little current (green) we will again hit the downward branch of the nullcline (as before) with a lot of current (grey) we will, however, hit the blue (other) nullcline and a etc. new spike will be elicited! etc. 64

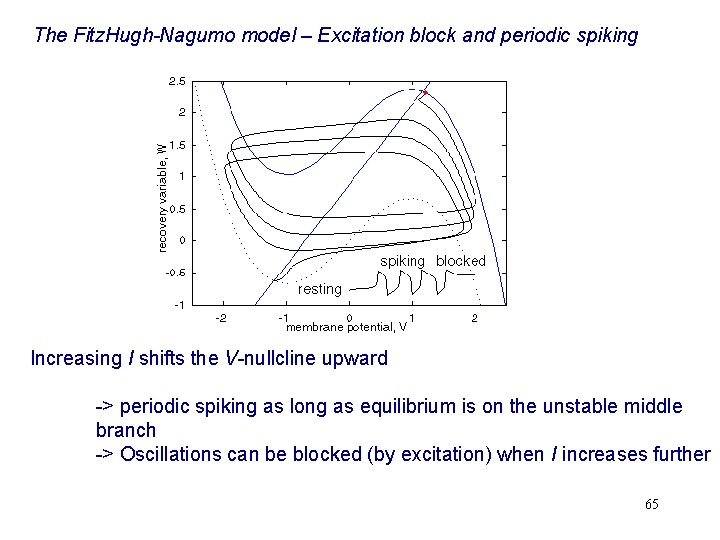
The Fitz. Hugh-Nagumo model – Excitation block and periodic spiking Increasing I shifts the V-nullcline upward -> periodic spiking as long as equilibrium is on the unstable middle branch -> Oscillations can be blocked (by excitation) when I increases further 65

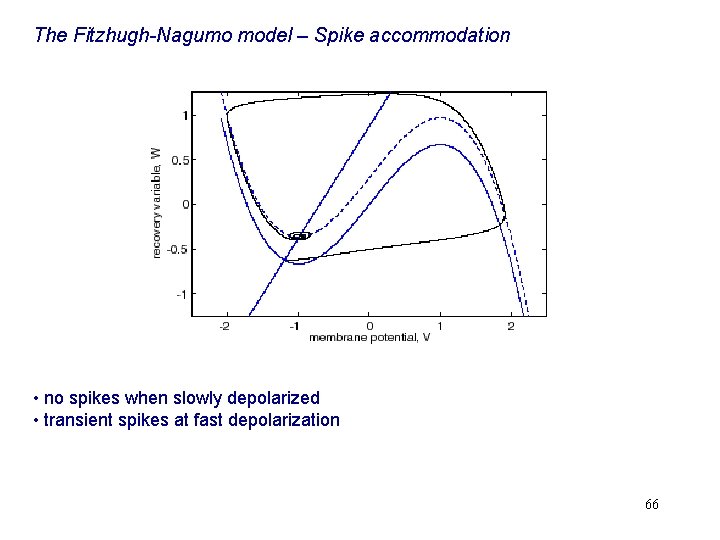
The Fitzhugh-Nagumo model – Spike accommodation • no spikes when slowly depolarized • transient spikes at fast depolarization 66

Neuronal codes Spiking models: • Hodgkin Huxley Model (brief repetition) • Reduction of the HH-Model to two dimensions (general) • Fitz. Hugh-Nagumo Model • Integrate and Fire Model 67

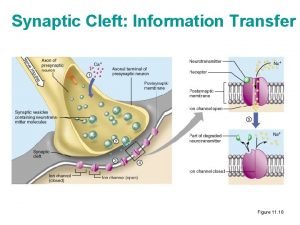
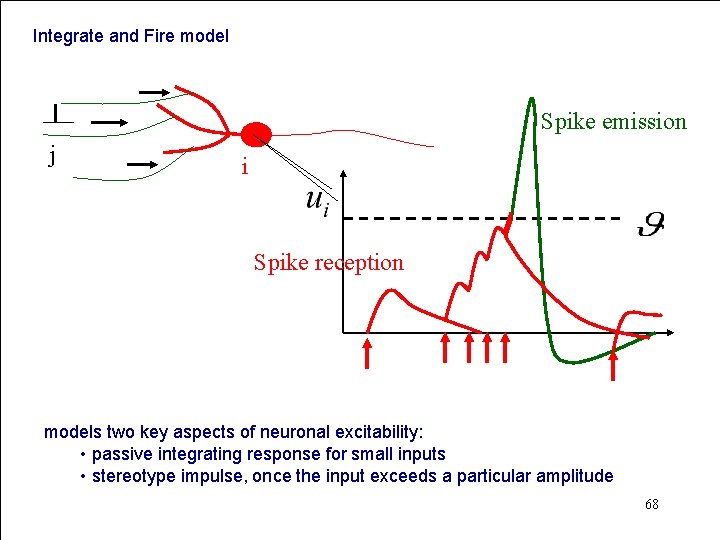
Integrate and Fire model Spike emission j i Spike reception models two key aspects of neuronal excitability: • passive integrating response for small inputs • stereotype impulse, once the input exceeds a particular amplitude 68

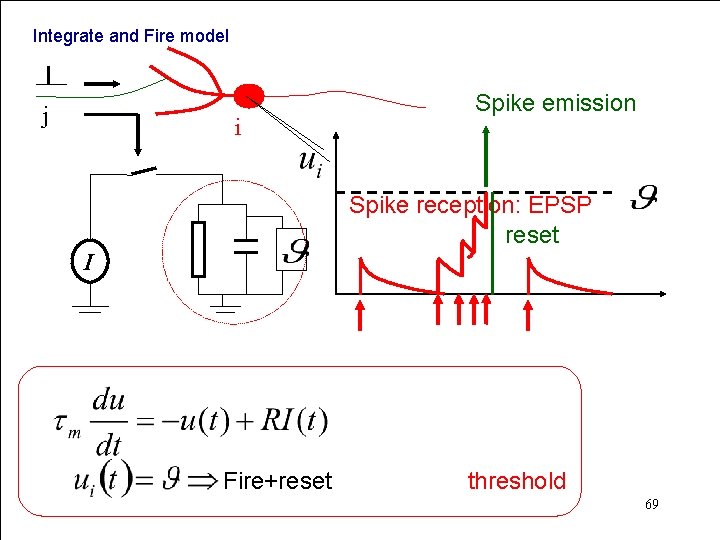
Integrate and Fire model j i Spike emission Spike reception: EPSP reset I Fire+reset threshold 69

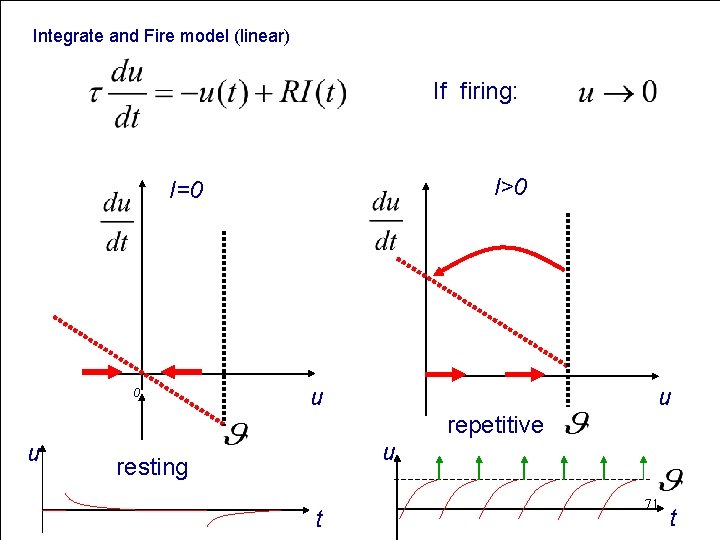
Integrate and Fire model (linear) If firing: I>0 I=0 0 u u resting t repetitive 71 t

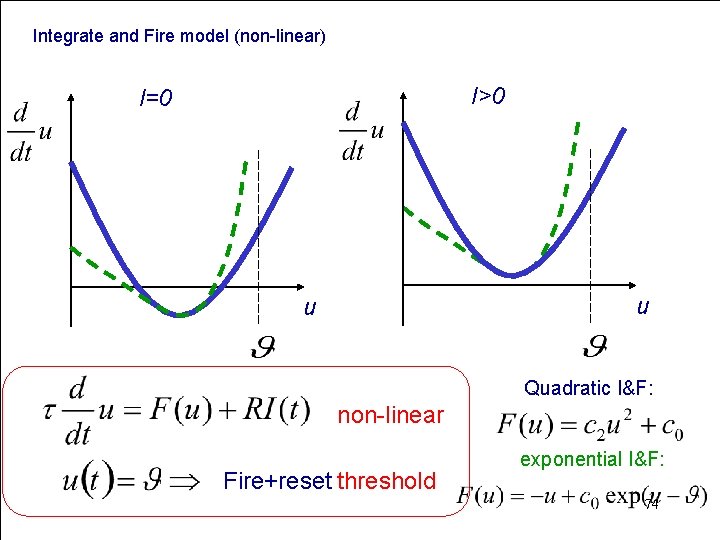
Integrate and Fire model linear non-linear If firing: 72

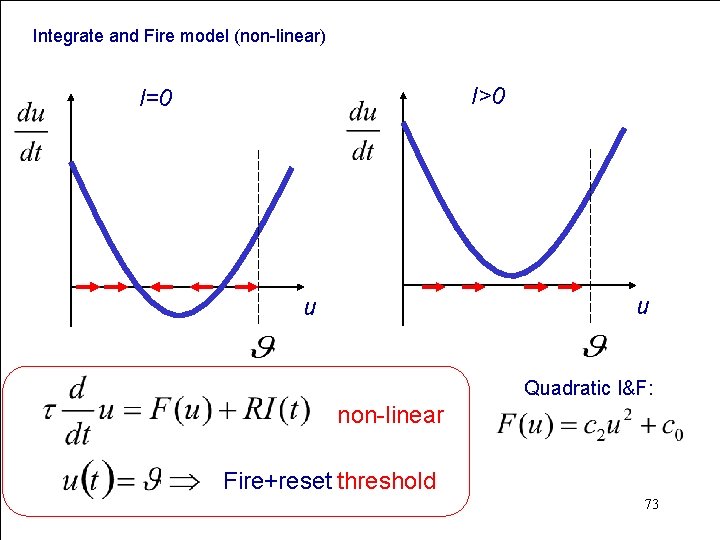
Integrate and Fire model (non-linear) I>0 I=0 u u Quadratic I&F: non-linear Fire+reset threshold 73

Integrate and Fire model (non-linear) I>0 I=0 u u Quadratic I&F: non-linear Fire+reset threshold exponential I&F: 74

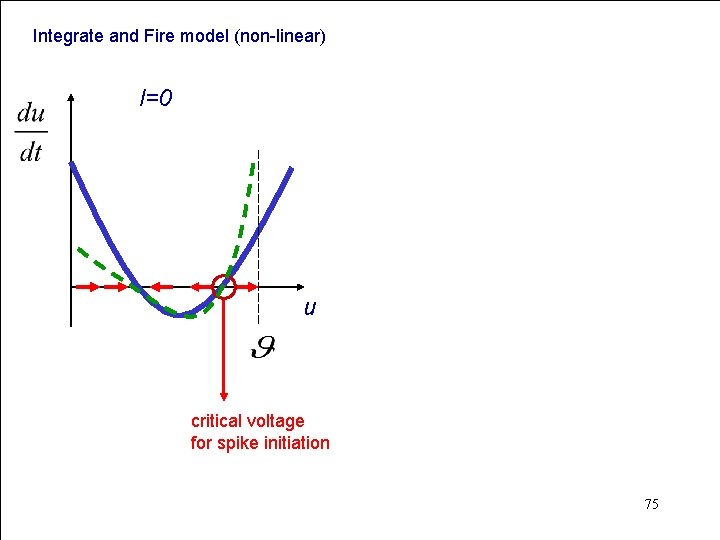
Integrate and Fire model (non-linear) I=0 u critical voltage for spike initiation 75

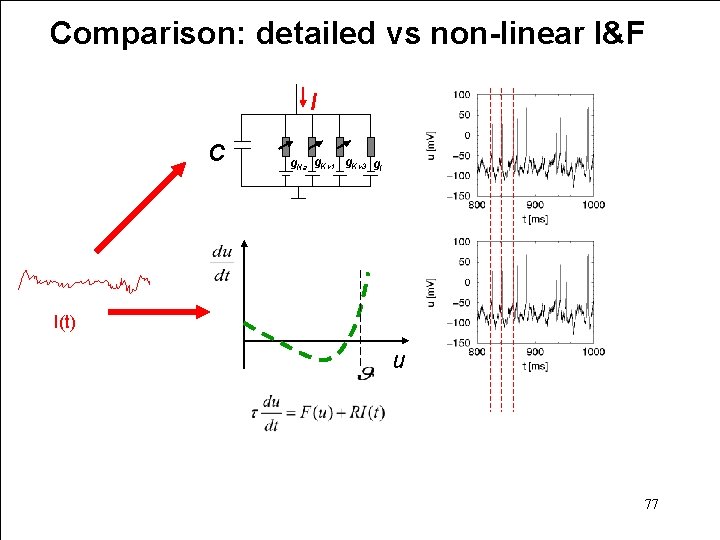
Comparison: detailed vs non-linear I&F I C g. Na g. Kv 1 g. Kv 3 gl I(t) u 77

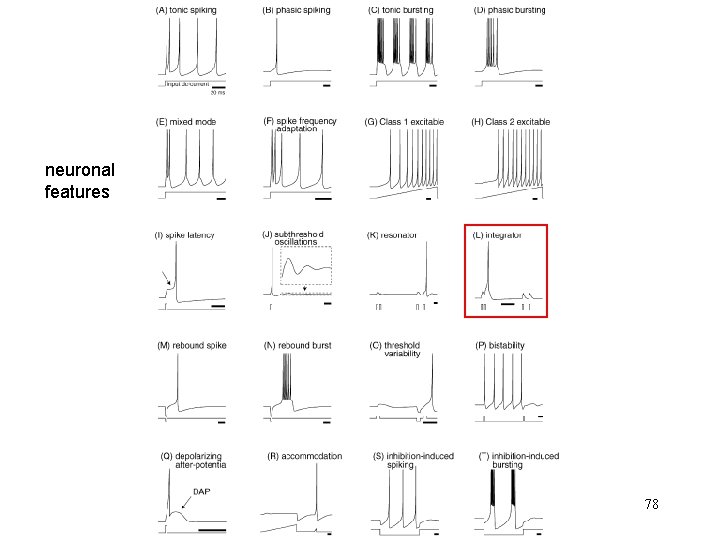
neuronal features 78

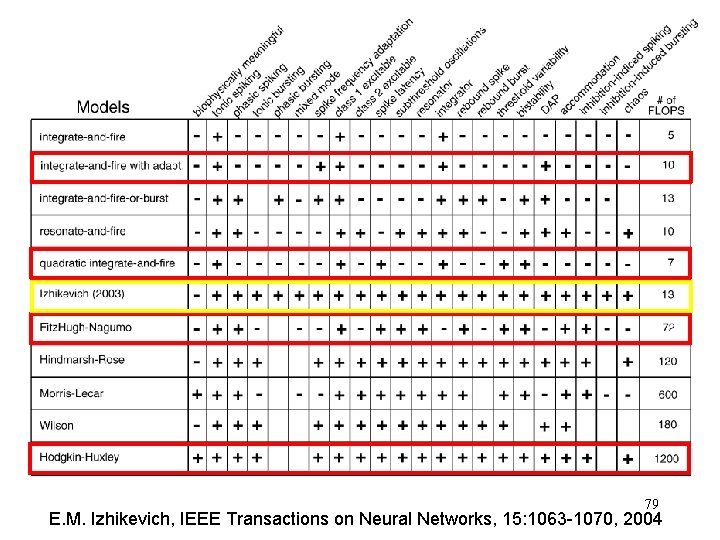
79 E. M. Izhikevich, IEEE Transactions on Neural Networks, 15: 1063 -1070, 2004

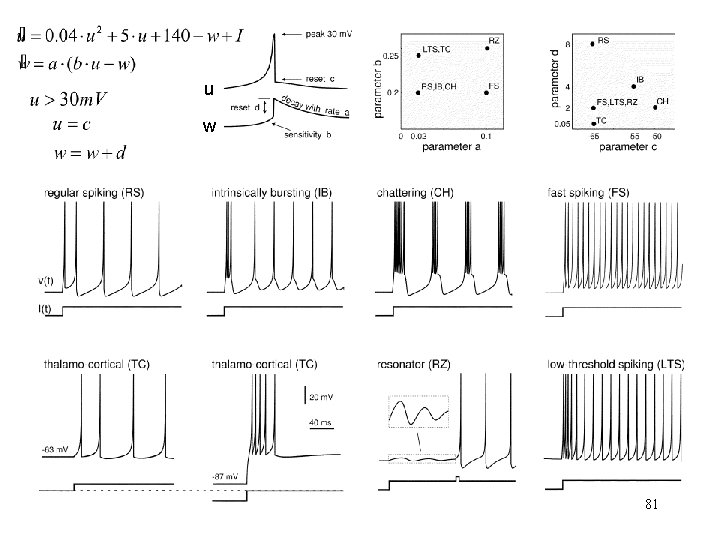
E. M. Izhikevich, 2003 if threshold 80

u w 81

End here 82

Neuronal codes Spiking models: • Hodgkin Huxley Model (small regeneration) • Reduction of the HH-Model to two dimensions (general) • Fitz. Hugh-Nagumo Model • Integrate and Fire Model • Spike Response Model 83

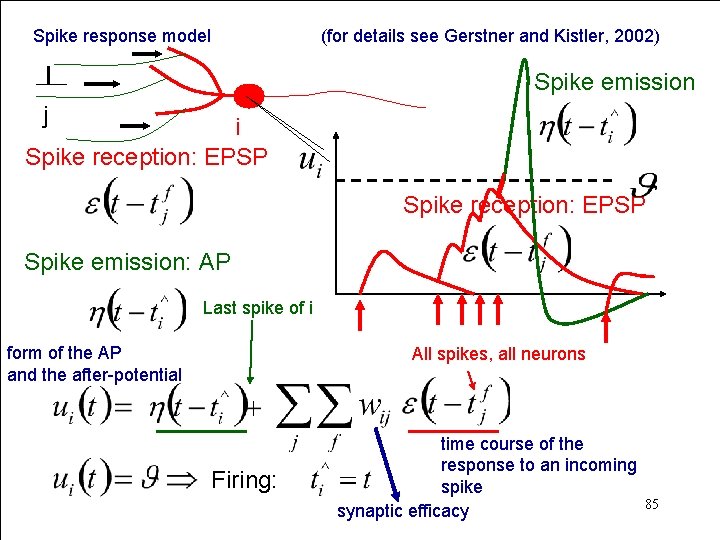
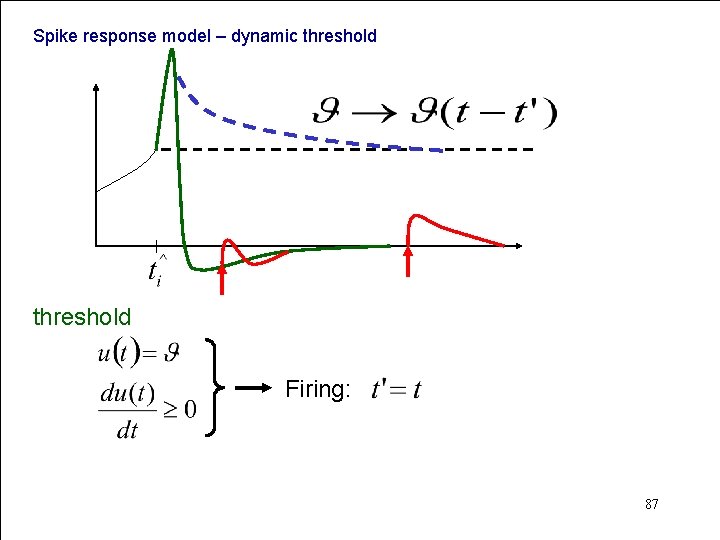
Spike response model (for details see Gerstner and Kistler, 2002) = generalization of the I&F model SRM: I&F: • parameters depend on the time since the last output spike • voltage dependent parameters • integral over the past • differential equations allows to model refractoriness as a combination of three components: 1. reduced responsiveness after an output spike 2. increase in threshold after firing 3. hyperpolarizing spike after-potential 84

Spike response model (for details see Gerstner and Kistler, 2002) Spike emission j i Spike reception: EPSP Spike emission: AP Last spike of i form of the AP and the after-potential All spikes, all neurons Firing: time course of the response to an incoming spike synaptic efficacy 85

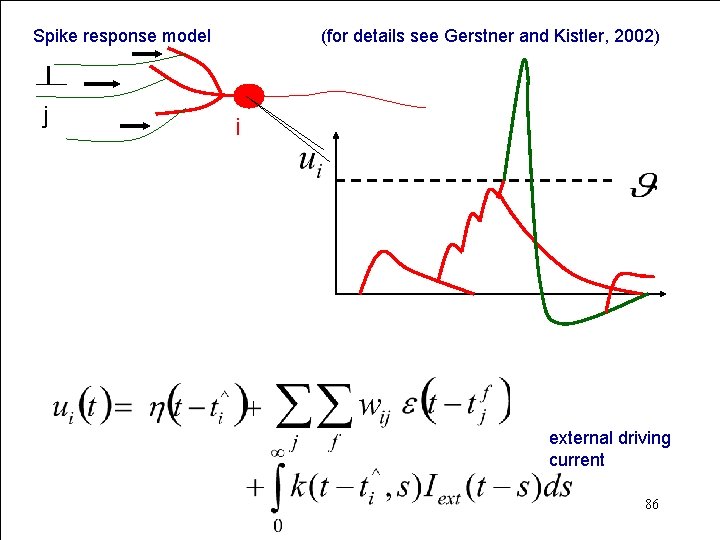
Spike response model j (for details see Gerstner and Kistler, 2002) i external driving current 86

Spike response model – dynamic threshold Firing: 87

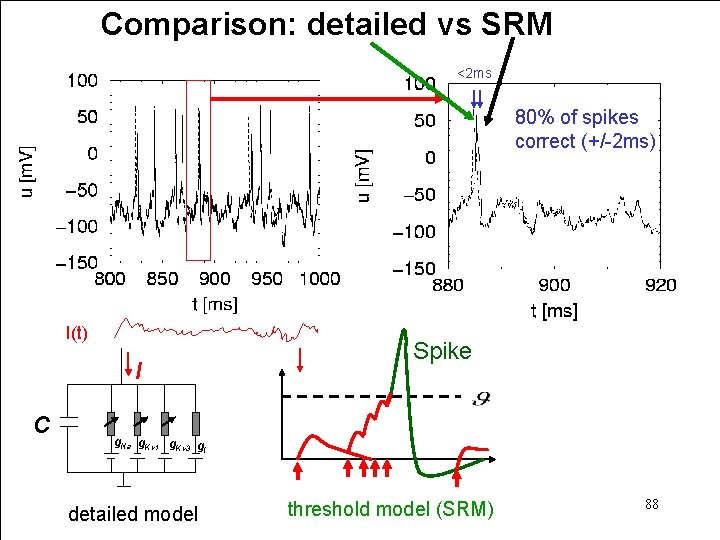
Comparison: detailed vs SRM <2 ms 80% of spikes correct (+/-2 ms) I(t) I C Spike g. Na g. Kv 1 g. Kv 3 g l detailed model threshold model (SRM) 88

References • Rieke, F. et al. (1996). Spikes: Exploring the neural code. MIT Press. • Izhikevich E. M. (2007) Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. MIT Press. • Fitzhugh R. (1961) Impulses and physiological states in theoretical models of nerve membrane. Biophysical J. 1: 445 -466 • Nagumo J. et al. (1962) An active pulse transmission line simulating nerve axon. Proc IRE. 50: 2061– 2070 • Gerstner, W. and Kistler, W. M. (2002) Spiking Neuron Models. Cambridge University Press. online at: http: //diwww. epfl. ch/~gerstner/SPNM. html 89