Socle commun des connaissances et des comptences La

Socle commun des connaissances et des compétences La colonne vertébrale de l’enseignement obligatoire ! Animations pédagogiques Février Mars 2008 Inspection pédagogique régionale de mathématiques 1

Évolution rapide de la société Faibles besoins en personnes hautement qualifiées Forts besoins en personnes hautement qualifiées Connaissances dans les livres Diversification des sources de connaissances Conseil européen de Lisbonne (mars 2000) Programme International de Suivi des Acquis des élèves (PISA) 2

Une mission nouvelle pour l’école L’article 9 de la loi d’orientation et de programme pour l’avenir de l’école du 23 avril 2005 « la scolarité obligatoire doit au moins garantir à chaque élève les moyens nécessaires à l’acquisition d’un socle commun constitué d’un ensemble de connaissances et de compétences qu’il est indispensable de maîtriser pour accomplir avec succès sa scolarité, poursuivre sa formation, construire son avenir personnel et professionnel et réussir sa vie en société » Le décret n° 2006 -830 relatif au socle commun « Il (le socle) détermine ce que nul n’est censé ignorer en fin de scolarité obligatoire sous peine de se trouver marginalisé ou handicapé. » 100% des élèves maîtrisent 100% des connaissances et compétences du socle 3

Les 7 compétences • la maîtrise de la langue française • la pratique d’une langue vivante étrangère • les compétences de base en mathématiques et la culture scientifique et technologique • la maîtrise des techniques usuelles de l’information et de la communication • la culture humaniste • les compétences sociales et civiques • l’autonomie et l’initiative 4

Socle commun • Connaissances • Capacités • Attitudes « Chaque grande compétence du socle est conçue comme une combinaison de connaissances fondamentales pour notre temps, de capacités à les mettre en oeuvre dans des situations variées, mais aussi d'attitudes indispensables tout au long de la vie, comme l'ouverture aux autres, le goût pour la recherche de la vérité, le respect de soi et d'autrui, la curiosité et la créativité. » 5

Une particularité française Le socle commun ne se substitue pas aux programmes Les connaissances et les capacités exigibles dans le cadre du socle sont inclues dans les programmes d’enseignement Des textes en appui pour accompagner la mise en œuvre : BO N° 6 du 19 avril 2007 pour les programmes de Mathématiques, de Sciences et Vie de la Terre, de Physique-Chimie. 6

Le Socle commun : Un enseignement minimaliste ou une grande ambition ? Quelques exemples de capacités exigibles dans le cadre du socle : – Pilier 3 A : Les principaux éléments de Mathématiques – Pilier 3 B : Les principaux éléments de la culture scientifique et technologique – Pilier 5 : La culture humaniste – Pilier 6 : Les compétences sociales et civiques – Pilier 7 : Autonomie et initiative 7

Le socle commun ? Une belle ambition et une grande exigence ! Une priorité : S’y mettre ! 8

Quels objectifs avoir ? • Proposer des contenus et des situations qui fassent sens pour TOUS les élèves. • Obtenir que TOUS les élèves soient en réelle activité intellectuelle dans la classe. « Offrir à chacun les moyens de développer toutes ses facultés en mettant en valeur toutes les formes d’intelligence et toutes les aptitudes » (Cf. Eduscol) 9

Comment parvenir, dans le quotidien des cours de mathématiques, à construire pour tout élève les compétences du socle commun ? 10

Mettre à tout moment tout élève en activité mathématique Proposition n° 1 : Effectuer un calcul peut être l’occasion d’une réelle activité mathématique. 11

Donner (redonner ? ) toute sa noblesse au calcul. • la maîtrise du calcul et du sens des opérations est une priorité • effectuer mentalement un calcul réfléchi est l’occasion d’une vraie activité mathématique. Toutefois • la priorité n’est pas le calcul posé. Appliquer une technique non comprise n’est pas une activité mathématique. 12

Mettre à tout moment tout élève en activité mathématique Proposition N° 2 : Veiller à donner des activités qui soient occasion d’apprentissage pour tous. Analyse de trois séries de problèmes. 1. Chaque problème est-il un problème accessible à tous ? 2. Chaque problème offre -t–il une vraie activité mathématique pour tout élève, autrement dit est-il un problème qui a de l’avenir pour tout élève ? 3. Si oui, avec quels exigibles du socle commun pourrait-il être résolu ? Comment ? A quel palier ? 4. Série N° 1 Série N° 2 Série N° 3 13

Mettre à tout moment tout élève en activité mathématique Proposition N° 3 : Revenir souvent, et par petites touches, sur une même notion en institutionnalisant à toute séance un temps d’activités rapides. 14

Quelques intérêts des temps d’activités rapides • différer la formalisation d’une stratégie de calcul pour que tous puissent lui donner du sens • entretenir les acquis durablement et les travailler en dehors du contexte dans lequel ils ont été construits. • construire et entretenir des automatismes et en particulier maintenir jusqu’en troisième une mobilisation des tables de multiplication « dans tous les sens » . 15

Mettre à tout moment tout élève en activité mathématique Proposition n° 4 : Adopter des stratégies de différenciation pédagogique. 16

Comment s’y prendre pour que chaque élève s’engage dans un travail et avance sur ses difficultés tout en conservant un avancement collectif de la classe ? Piste n° 1 : Avoir sur une même activité des exigences différentes en jouant sur les paramètres didactiques de manière à aménager des niveaux de maîtrise technique différents. Un exemple en classe de 6 ième 17

Mais comment s’y prendre en classe pour que chaque élève s’engage dans un travail et avance sur ses difficultés tout en conservant un fonctionnement de classe ? Piste n° 2 : Laisser le temps nécessaire aux élèves plus lents • en ciblant pour une séance une ou deux situations permettant de construire des compétences incontournables • en laissant aux élèves plus lents le temps dont ils ont besoin pour traiter ces deux situations • en proposant aux élèves plus rapides « questions défi » . Un exemple en 4 ième 18

Mais comment s’y prendre en classe pour que chaque élève s’engage dans un travail et avance sur ses difficultés tout en conservant un fonctionnement de classe? Piste n° 3 : Confronter tous les élèves à une tâche complexe sans cher à obtenir coûte que tous la maîtrisent dans sa globalité. Un exemple en classe de troisième 19

Mettre à tout moment tout élève en activité mathématique Proposition n° 5 : Placer le raisonnement au cœur de toute activité mathématique 20

Placer le raisonnement au cœur de l’activité mathématique de tout élève 1. Développer le raisonnement dans tous les champs du programme - élaborer une stratégie pour conduire un calcul et mettre en place un élément de contrôle - utilisation en acte des théorèmes de la géométrie - gestion des données : extraire et organiser l’information. 21

Placer le raisonnement au cœur de l’activité mathématique de tout élève 2. Dissocier le raisonnement de la rédaction d’une démonstration - encourager des raisonnements exprimés à l’oral - encourager des écrits intermédiaires : schémas, textes imparfaits … - valoriser des démonstrations partielles 22

Placer le raisonnement au cœur de l’activité mathématique de tout élève. 3. Valoriser des approches empiriques - solutions exactes ou approchées par essais - erreurs - exploitation des TICE ou manipulations techniques. 23

BILAN Quelques pratiques à cultiver pour construire à tout moment l’activité mathématique de tout élève. 1. Faire de toute question une question ouverte 2. Laisser vivre en classe différentes stratégies 3. Mettre en place des stratégies de différenciation pédagogique. 4. Revenir souvent et par petites touches sur une notion 5. Placer le raisonnement au cœur de l’activité mathématique de tout élève. 24

Comment faire évoluer les pratiques d’évaluation ? 25

Comment faire évoluer les pratiques d’évaluation ? Faire évoluer la nature des questions posées en contrôle de manière à ce que ces travaux deviennent exploitables pour évaluer les compétences du socle commun. 26

Faire en sorte que dans les sujets de contrôle il y ait des exercices • Permettant à tout élève de montrer d’autres compétences qu’une simple restitution de savoir-faire automatisé • Donnant à tout élève un vrai problème à résoudre. • Permettant d’évaluer le raisonnement indépendamment de la rédaction de ce raisonnement. • Permettant d’évaluer la rédaction indépendamment du raisonnement. 27

Évaluer les productions des élèves en terme de compétences Les productions de trois élèves sur trois questions. 28

Évaluer les productions des élèves en terme de compétences • La production d’un élève sur un exercice peut ne pas avoir grande signification • Ne pas hésiter à évaluer les compétences montrées y compris au travers de productions entachées d’erreurs • cibler les objectifs d’évaluation donnés à certaines questions et ne pas toujours attendre une maîtrise technique de bout en bout. 29

30

Premier problème : Deux neuvièmes des élèves de sixième d’un collège ont choisi l’allemand comme première langue. Dans ce même collège il y a 180 élèves en sixième. Combien y a –t-il d’élèves de sixième qui font de l’allemand ? 31

Second problème : Pierre dépense les trois cinquièmes de son argent de poche à la librairie. Chaque mois il donne ainsi 48€ au libraire. Quel est le montant de l’argent de poche que Pierre a chaque mois ? 32

Troisième problème : Le premier jour, Yuna a parcouru les 3 septièmes de son voyage. Le lendemain, Yuna parcourt les 3 quarts du reste et enfin le troisième jour elle arrive après avoir parcouru 40 kilomètres. Quelle est la longueur de son voyage ? 33

Écart entre objectif du programme et exigence du socle commun. 34

Écart entre objectif du programme et exigence du socle commun. 35

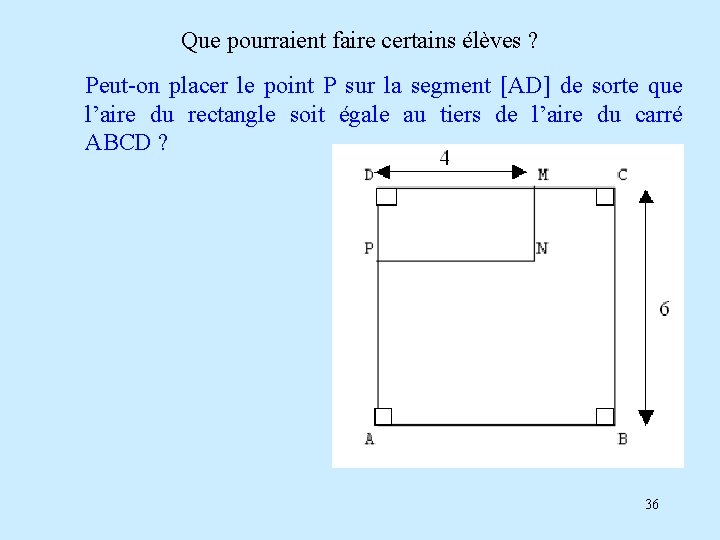
Que pourraient faire certains élèves ? Peut-on placer le point P sur la segment [AD] de sorte que l’aire du rectangle soit égale au tiers de l’aire du carré ABCD ? 36

Que pourraient faire certains élèves ? Peut-on placer le point P sur la segment [AD] de sorte que l’aire du rectangle soit égale au tiers de l’aire du carré ABCD ? 37

Que pourraient faire certains élèves ? Peut-on placer le point P sur la segment [AD] de sorte que l’aire du rectangle soit égale au tiers de l’aire du carré ABCD ? 38

Que pourraient faire certains élèves ? Peut-on placer le point P sur la segment [AD] de sorte que l’aire du rectangle soit égale au tiers de l’aire du carré ABCD ? 39

Que pourraient faire certains élèves ? Je prends 2 : 2+4= 6 ; 6 x 2 = 12 ; 12+4 = 16 ; carré de 4. 16 est le Je prends (-1) : -1+4= 3 ; 3 x (-1) = (-3) ; (-3)+4 = 1 ; est le carré de 1. 1 Avec 5 je trouve 49 donc le carré de 7 ; avec 8 je trouve 100 donc le carré de 10 ; avec (-4) je trouve 4 donc le carré de 2. Cela semble vrai mais je ne sais pas comment le prouver. 40

Que pourraient faire certains élèves ? Je prends 2 : 2+4= 6 ; 6 x 2 = 12 ; 12+4 = 16 ; 16 est le carré de 4. Avec 5 je trouve 49 donc le carré de 7 ; avec 8 je trouve 100 donc le carré de 10 ; avec (-4) je trouve 4 donc le carré de 2. Pour 2, le carré de 4; pour 5 le carré de 7; pour 8 le carré de 10, pour (-4) le carré de 2. Le résultat sera toujours le carré du nombre choisi augmenté de 2. 41

Que pourraient faire certains élèves ? Je prends 2 : 2+4= 6 ; 6 x 2 = 12 ; 12+4 = 16 ; 16 est le carré de 4. Pour 2, je trouve le carré de 4; pour 5 le carré de 7; pour 8 le carré de 10, pour (-4) le carré de 2. Je trouve à chaque fois le carré du nombre choisi augmenté de 2. Soit a le nombre. Le résultat est (a+4) x a + 4. Est ce pareil que le carré de (a+2) ? 42

Écart entre objectif du programme et exigence du socle commun • Programme de 3 ième : page 50 du BO N° 6 du 19 avril 2007 : Résolution de problème conduisant à une équation du premier degré à une inconnue La notion d’équation ne fait pas partie du socle commun. Néanmoins les élèves, dans le cadre du socle, pourront être amenés à résoudre des problèmes se ramenant à une équation du premier degré sans que la méthode experte ne soit exigible. Document d’accompagnement : du numérique au littéral. 43

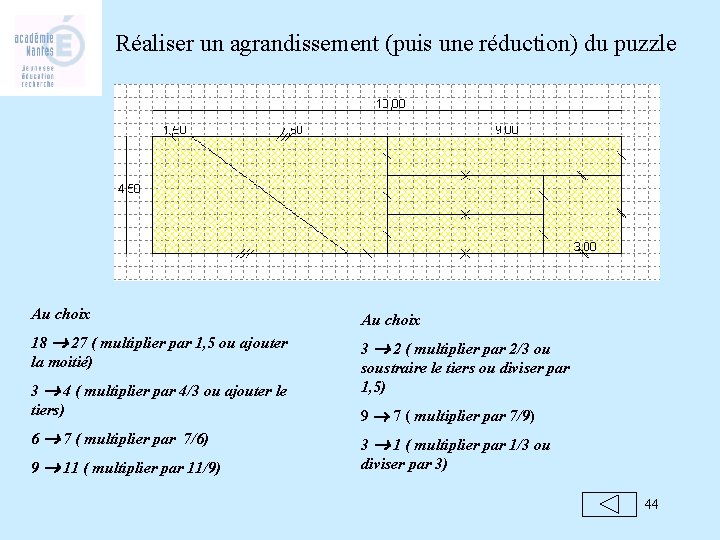
Réaliser un agrandissement (puis une réduction) du puzzle Au choix 18 27 ( multiplier par 1, 5 ou ajouter la moitié) 3 2 ( multiplier par 2/3 ou soustraire le tiers ou diviser par 1, 5) 3 4 ( multiplier par 4/3 ou ajouter le tiers) 6 7 ( multiplier par 7/6) 9 11 ( multiplier par 11/9) 9 7 ( multiplier par 7/9) 3 1 ( multiplier par 1/3 ou diviser par 3) 44

Exemple en 4 ième : Tangente à un cercle • Sont donnés un cercle C et un point A de ce cercle. Construire la droite tangente à C passant par le point A. • Sont donnés une droite (d) et un point O, non élément de (d). Construire le (un ? ) cercle de centre O tangent à cette droite. • Tracer un cercle de centre O et de rayon 4. Placer sur ce cercle deux points A et B tel que l’angle AOB mesure 70°. Construire le point C diamétralement opposé à A et tracer la tangente au cercle en A. Cette tangente coupe la droite (BC) en D. Calculer la mesure de chacun des angles du triangle ACD. 45

Un exemple en classe de troisième Problème posé: Construis un carré ABCD de côté 10 cm. Choisis un nombre compris entre 1 et 10 et place le point E sur le segment [DC] tel que la longueur du segment [DE] soit égale à ce nombre. Construis le point F du segment [BC] tel que DE=FC. Calcule l’aire du quadrilatère AECF. 46

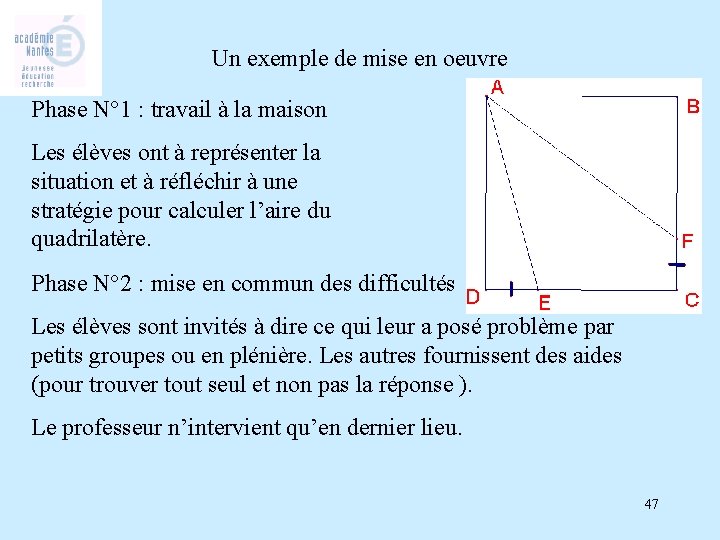
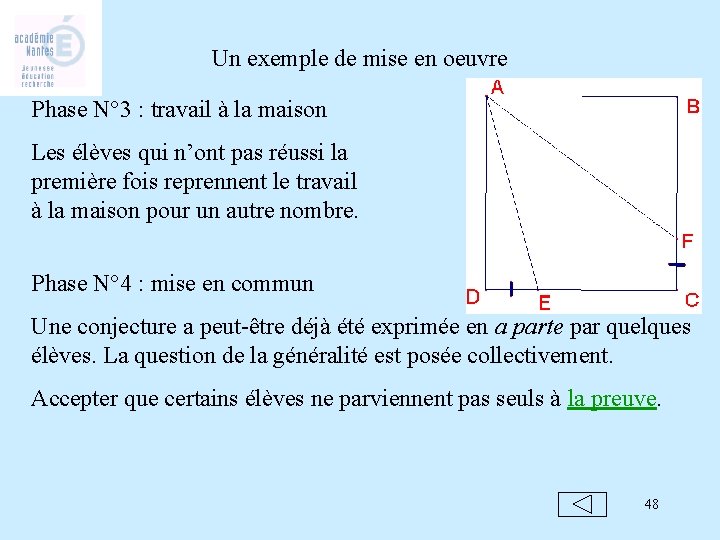
Un exemple de mise en oeuvre Phase N° 1 : travail à la maison Les élèves ont à représenter la situation et à réfléchir à une stratégie pour calculer l’aire du quadrilatère. Phase N° 2 : mise en commun des difficultés Les élèves sont invités à dire ce qui leur a posé problème par petits groupes ou en plénière. Les autres fournissent des aides (pour trouver tout seul et non pas la réponse ). Le professeur n’intervient qu’en dernier lieu. 47

Un exemple de mise en oeuvre Phase N° 3 : travail à la maison Les élèves qui n’ont pas réussi la première fois reprennent le travail à la maison pour un autre nombre. Phase N° 4 : mise en commun Une conjecture a peut-être déjà été exprimée en a parte par quelques élèves. La question de la généralité est posée collectivement. Accepter que certains élèves ne parviennent pas seuls à la preuve. 48

Utilisation en acte des théorèmes de la géométrie Sur la figure ci-contre : - A, B et E sont alignés ; - A, C et D sont alignés. Dans chaque cas, les droites (BC) et (ED) sont-elles parallèles ? Justifier la réponse en faisant des calculs (on ne demande aucune rédaction, seulement des calculs). Cas 1 : AB=8, 5 ; AC= 7, 7 ; BC= 3, 6 et l’angle ADE est droit. Cas 2 : AB=8, 5 ; AC=7, 7 ; BE=2, 04 et AD =9, 548 49

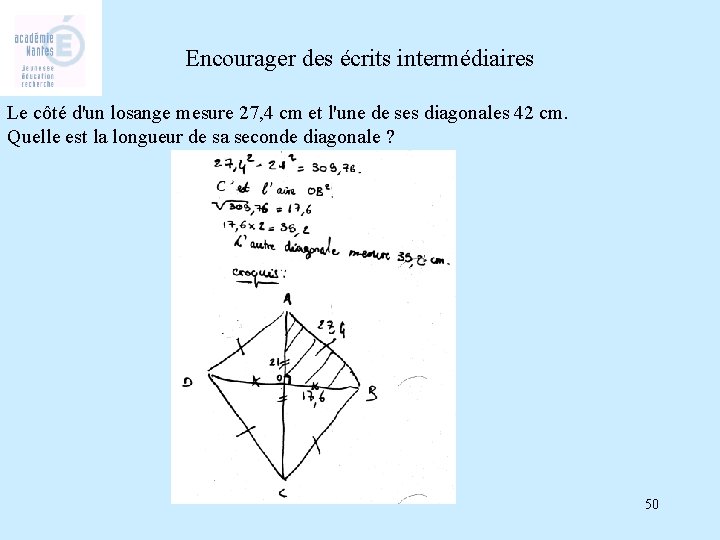
Encourager des écrits intermédiaires Le côté d'un losange mesure 27, 4 cm et l'une de ses diagonales 42 cm. Quelle est la longueur de sa seconde diagonale ? 50

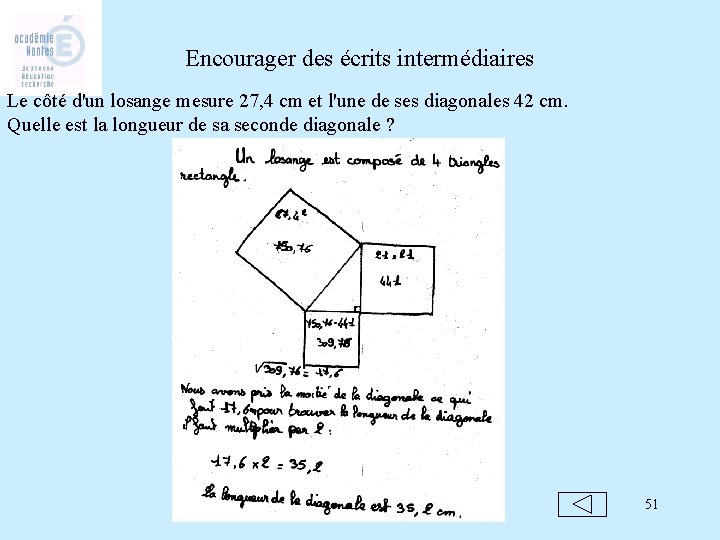
Encourager des écrits intermédiaires Le côté d'un losange mesure 27, 4 cm et l'une de ses diagonales 42 cm. Quelle est la longueur de sa seconde diagonale ? 51

Encourager des démonstrations partielles Sur la figure ci-contre : ABC est un triangle rectangle en A I est le milieu de [AC] J est le milieu de [BC]. AB = 4 et AC = 7. On voudrait trouver une relation entre les aires des triangles ABC et CIJ. 52

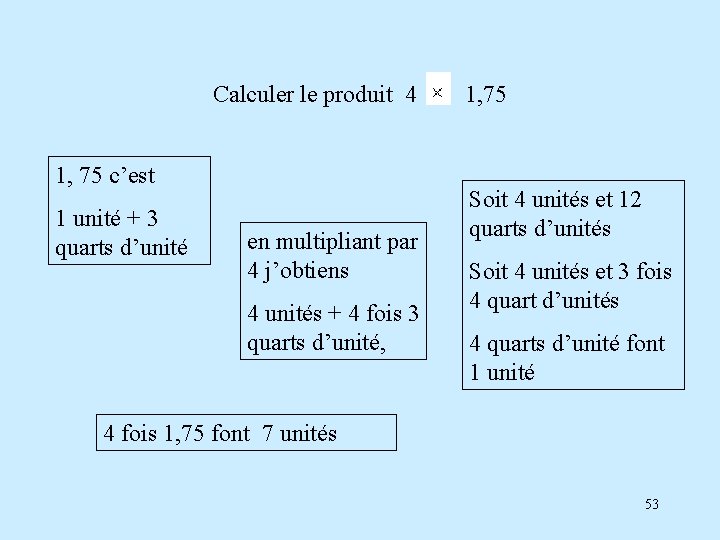
Calculer le produit 4 1, 75 c’est 1 unité + 3 quarts d’unité en multipliant par 4 j’obtiens 4 unités + 4 fois 3 quarts d’unité, 1, 75 Soit 4 unités et 12 quarts d’unités Soit 4 unités et 3 fois 4 quart d’unités 4 quarts d’unité font 1 unité 4 fois 1, 75 font 7 unités 53

Calculer le produit 4 Pour multiplier 1, 75 par 4 je vais le multiplier deux fois par 2 1, 75 2 fois 3, 5 2 fois 1, 75 c’est 1, 75+1, 75 c’est 3, 5+3, 5 Soit 7. Soit 3, 5 4 fois 1, 75 font 7 54

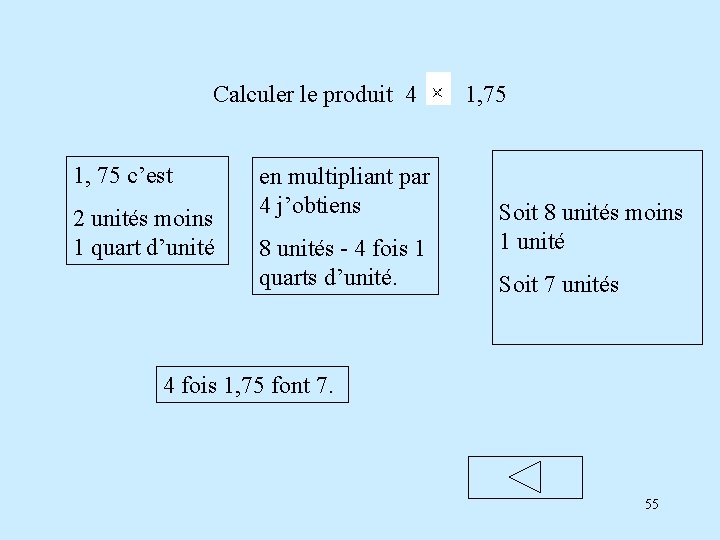
Calculer le produit 4 1, 75 c’est 2 unités moins 1 quart d’unité en multipliant par 4 j’obtiens 8 unités - 4 fois 1 quarts d’unité. 1, 75 Soit 8 unités moins 1 unité Soit 7 unités 4 fois 1, 75 font 7. 55

Pilier 3 A : Les principaux éléments de Mathématiques « Saisir quand une situation de la vie courante se prête à un traitement mathématique, l’analyser en posant les données puis en émettant des hypothèses, s’engager dans un raisonnement ou un calcul en vue de sa résolution » 56

Pilier 3 B : Les principaux éléments de la culture scientifique et technologique « Pratiquer une démarche scientifique : savoir observer, questionner, formuler une hypothèse et la valider, modéliser de façon élémentaire… » 57

Pilier 5 : La culture humaniste • « Situer dans le temps les événements, les œuvres littéraires ou artistiques, les découvertes scientifiques ou techniques étudiés et de les mettre en relation avec des faits historiques ou culturels utiles à leur compréhension » • « Mobiliser les connaissances pour donner du sens à l’actualité » 58

Pilier 6 : Les compétences sociales et civiques « Savoir construire son opinion personnelle et pouvoir la remettre en question, la nuancer (par la prise de conscience de la part d’affectivité, de l’influence de préjugés, de stéréotypes) » 59

Pilier 7 : Autonomie et initiative « être capable de raisonner avec logique et rigueur et donc savoir : – Identifier un problème et mettre au point une démarche de résolution, – Recher l’information utile, l’analyser, la trier, la hiérarchiser, l’organiser, la synthétiser. – Mettre en relation les acquis des différentes disciplines, les mobiliser dans des situations variées, – Identifier, expliquer, rectifier une erreur, – Distinguer ce dont on est sûr de ce qu’il faut prouver – Mettre à l’essai plusieurs pistes de résolution » 60