Division euclidienne PGCD de 12 et 18 PGCD

Division euclidienne PGCD de 12 et 18 PGCD de 20 et 35 Algorithme des différences PGCD de 210 et 126 PGCD de 192 et 120 Algorithme d'Euclide Fraction irréductible Nombres premiers entre eux

Est-ce que 2 est un diviseur de 18 ? Oui Que signifie "2 est un diviseur de 18" ? Cela veut dire que si on divise 18 par 2, le quotient est entier et le reste est zéro. On dit aussi : 18 est un multiple de 2

Définition a et d désignent deux entiers tels que d 0. On dit que d est un diviseur de a si le reste de la division euclidienne de a par d est égal à 0.

Dans le cas de la division euclidienne, le dividende, le diviseur, le quotient et le reste sont des nombres entiers.

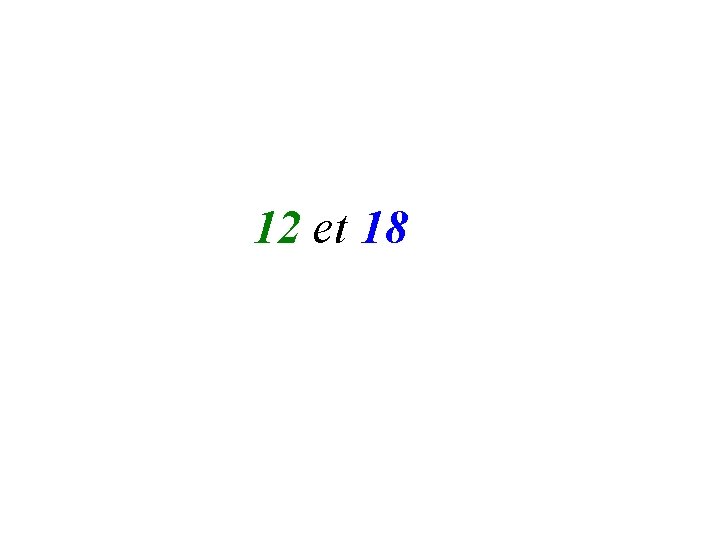
12 et 18

Diviseurs de 12 : 1 ; 2 ; 3 ; 4 ; 6 ; 12 Diviseurs de 18 : 1 ; 2 ; 3 ; 6 ; 9 ; 18 Diviseurs communs à 12 et 18 : 1 ; 2 ; 3 ; 6 Quel est le plus grand ? 6 On écrit PGCD (12 ; 18) = 6

On écrit PGCD (12 ; 18) = 6 Que signifie PGCD (12 ; 18) ? Plus Grand Commun Diviseur

Parmi les diviseurs communs à deux nombres entiers a et b, l’un deux est plus grand que les autres : on l’appelle le Plus Grand Commun Diviseur à a et b et on le note PGCD (a ; b).

Chercher PGCD (20 ; 35) Diviseurs de 20 : 1 ; 2 ; 4 ; 5 ; 10 ; 20 Diviseurs de 35 : 1 ; 5 ; 7 ; 35 Diviseurs communs à 20 et 35 : 1 ; 5 PGCD (20 ; 35) = 5

Chercher le PGCD va être parfois un peu long en écrivant tous les diviseurs, mais il existe des méthodes plus rapides. On appelle ces méthodes algorithmes. Un algorithme est une méthode de calcul où on répète le même procédé jusqu'au résultat trouvé.

Recherche du PGCD par la méthode des soustractions successives ou algorithme des différences

Propriété admise : Si a et b sont deux nombres entiers tels que a > b alors PGCD (a ; b) = PGCD(b ; a – b) Le plus petit La différence

PGCD (a ; b) = PGCD(b ; a – b) Le plus petit La différence Chercher le PGCD de 36 et 24 a - b 36 12 24 On soustrait les deux nombres donnés : 36 – 24 = 12 Plus grand a Plus petit b

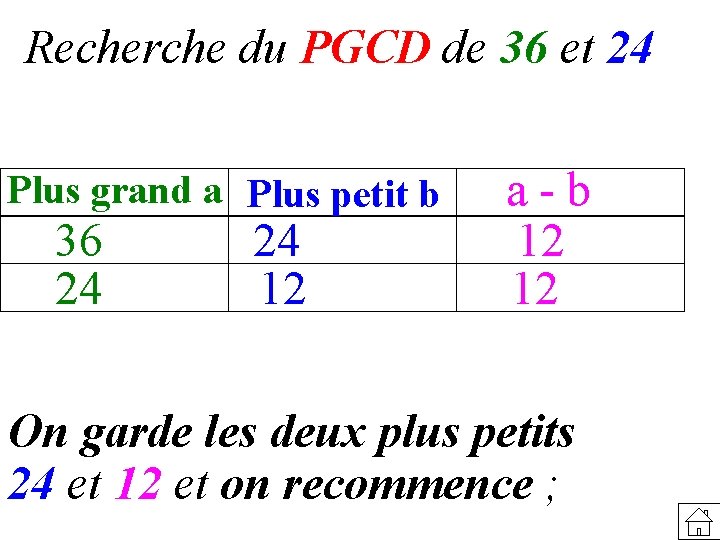
Recherche du PGCD de 36 et 24 Plus grand a Plus petit b 36 24 24 12 a - b 12 12 On garde les deux plus petits 24 et 12 et on recommence ;

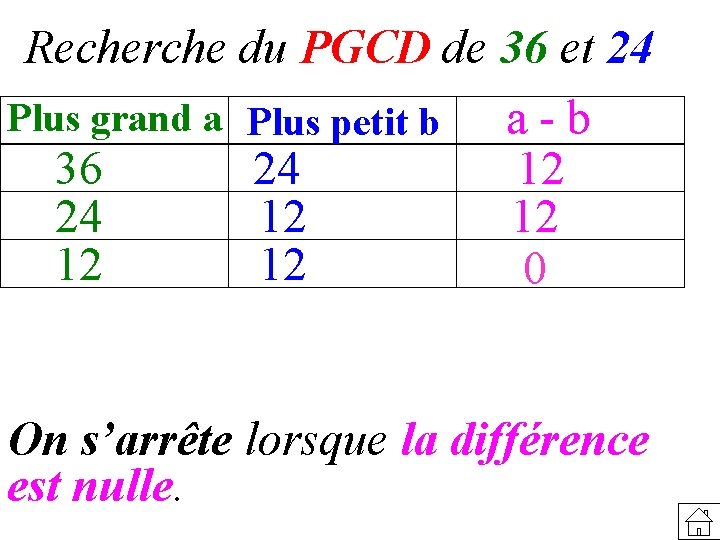
Recherche du PGCD de 36 et 24 Plus grand a Plus petit b a - b 36 24 12 12 0 On s’arrête lorsque la différence est nulle.

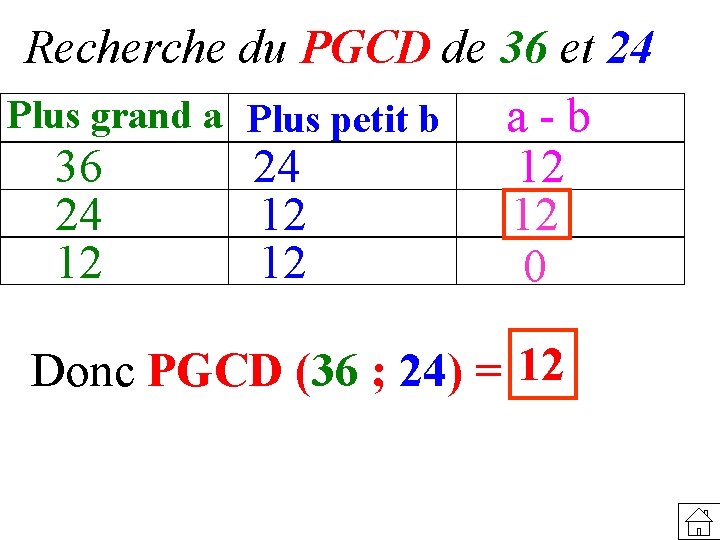
Recherche du PGCD de 36 et 24 Plus grand a Plus petit b a - b 36 24 12 12 0 Donc PGCD (36 ; 24) = 12

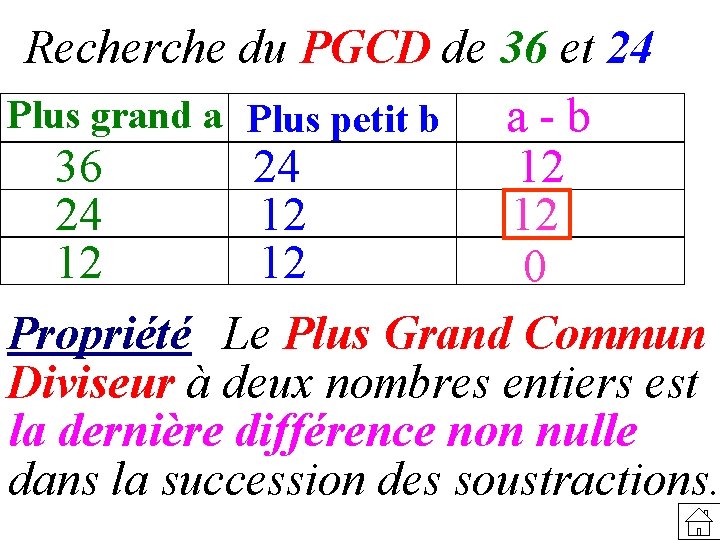
Recherche du PGCD de 36 et 24 Plus grand a Plus petit b a - b 36 24 12 12 0 Propriété Le Plus Grand Commun Diviseur à deux nombres entiers est la dernière différence non nulle dans la succession des soustractions.

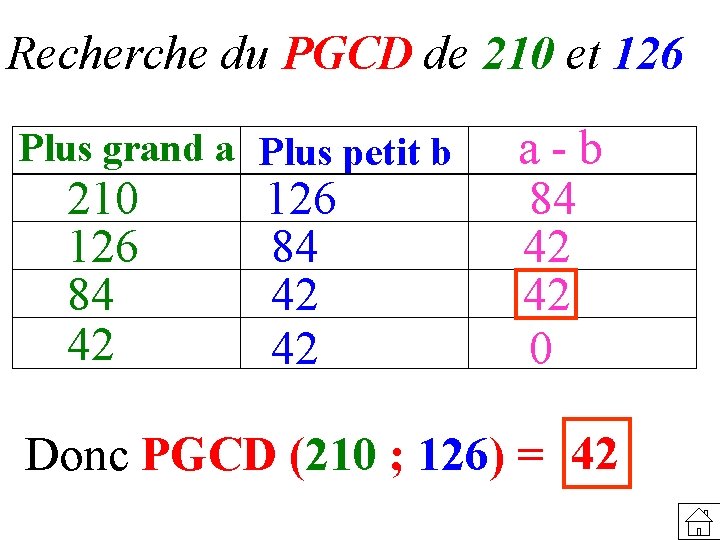
Recherche du PGCD de 210 et 126 Plus grand a Plus petit b 210 126 84 42 42 a - b 84 42 42 0 Donc PGCD (210 ; 126) = 42

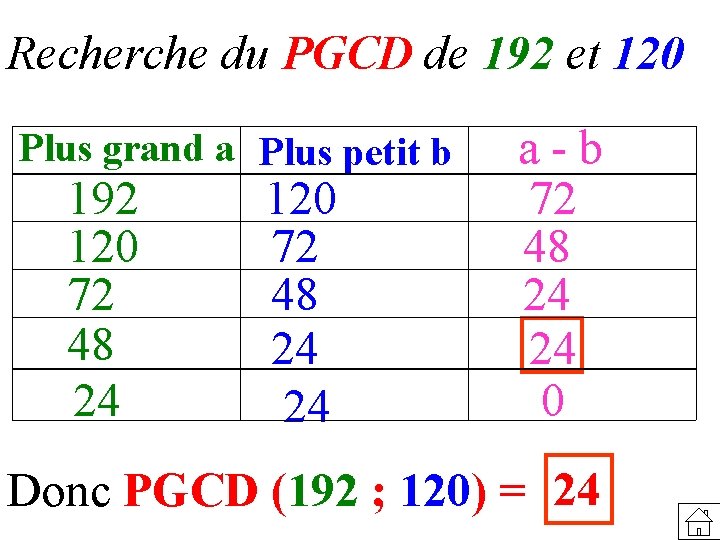
Recherche du PGCD de 192 et 120 Plus grand a Plus petit b 192 120 72 48 24 24 a - b 72 48 24 24 0 Donc PGCD (192 ; 120) = 24

Au lieu de faire les calculs à la main, on peut utiliser un logiciel. C'est un tableur. Nous allons calculer PGCD (45; 18) avec un tableur

Recherche du PGCD par la méthode des divisions successives ou algorithme d’Euclide d'Alexandrie vers 325 av JC - vers 265 av JC

Propriété admise : Si a et b sont deux nombres entiers tels que a > b alors PGCD (a ; b) = PGCD(b ; r) Le plus petit a r b q Reste de la division euclidienne de a par b

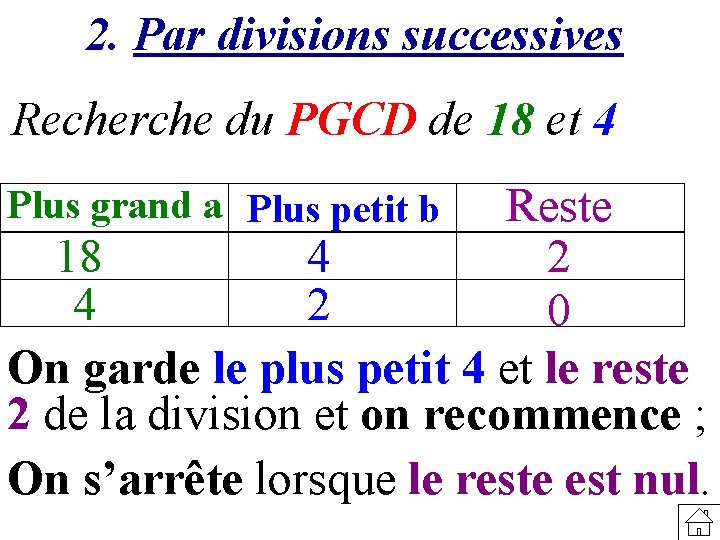
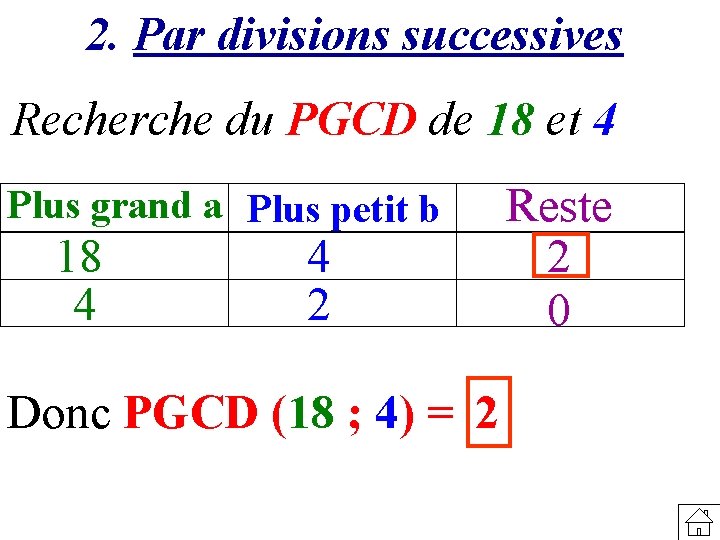
2. Par divisions successives Recherche du PGCD de 18 et 4 Plus grand a Plus petit b 18 4 Reste 2 On divise le plus grand nombre 18 par le plus petit 4 ;

2. Par divisions successives Recherche du PGCD de 18 et 4 Reste 18 4 2 0 On garde le plus petit 4 et le reste 2 de la division et on recommence ; On s’arrête lorsque le reste est nul. Plus grand a Plus petit b

2. Par divisions successives Recherche du PGCD de 18 et 4 Plus grand a Plus petit b 18 4 4 2 Donc PGCD (18 ; 4) = 2 Reste 2 0

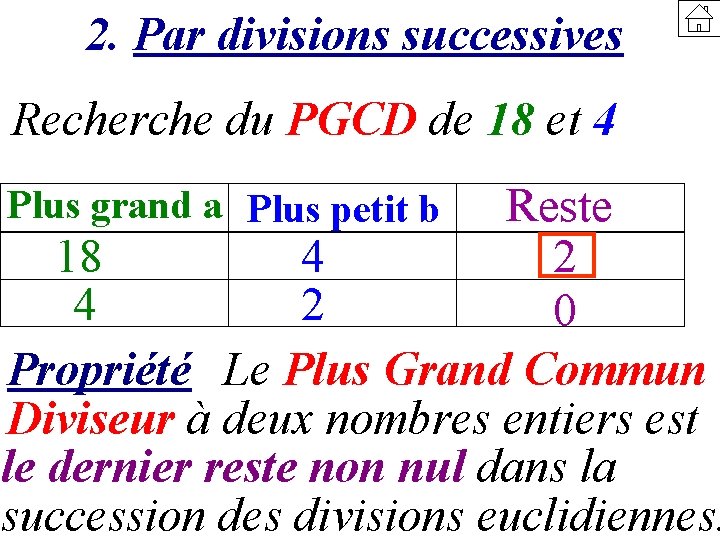
2. Par divisions successives Recherche du PGCD de 18 et 4 Reste 18 4 2 0 Propriété Le Plus Grand Commun Diviseur à deux nombres entiers est le dernier reste non nul dans la succession des divisions euclidiennes. Plus grand a Plus petit b

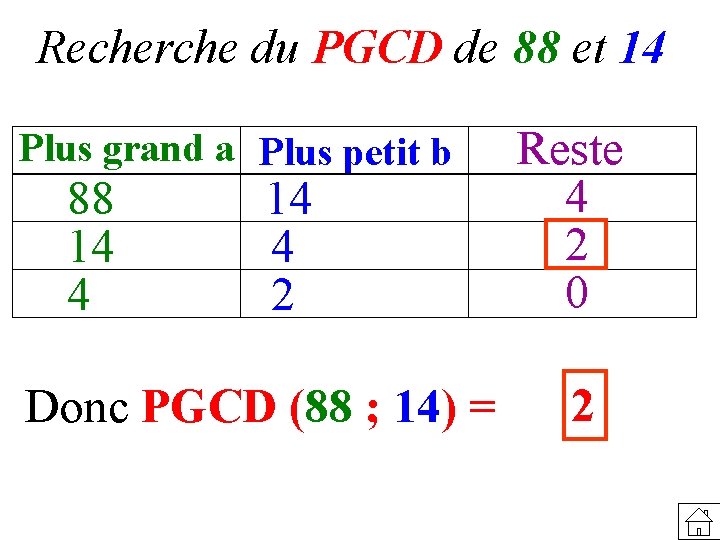
Recherche du PGCD de 88 et 14 Plus grand a Plus petit b 88 14 4 2 Donc PGCD (88 ; 14) = Reste 4 2 0 2

Fraction irréductible

On dit qu’une fraction est irréductible lorsque on ne peut plus la simplifier. 132 Rendre irréductible la fraction 77 On peut procéder par tâtonnement, mais il y a plus simple : trouver le Plus Grand Commun Diviseur à 132 et 77.

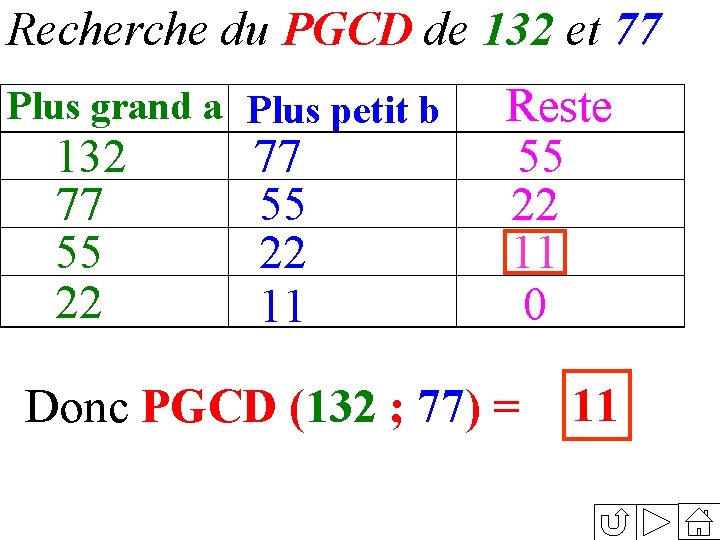
Recherche du PGCD de 132 et 77 Méthode des soustractions successives ou algorithme des différences Méthode des divisions successives ou algorithme d’Euclide

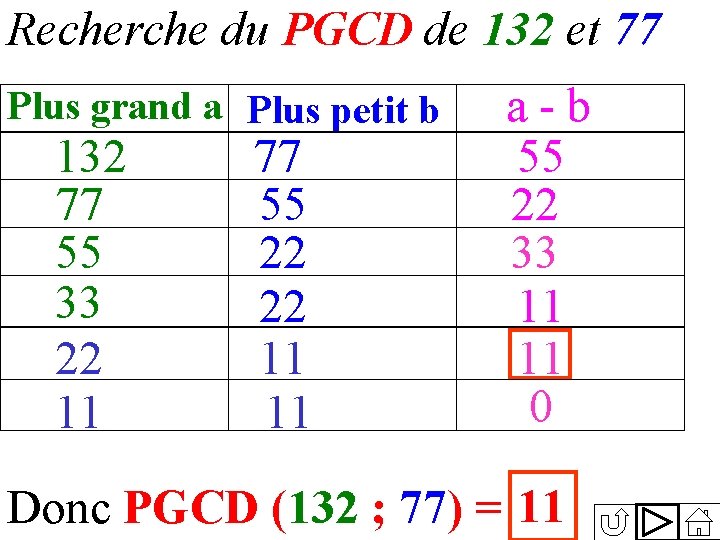
Recherche du PGCD de 132 et 77 Plus grand a Plus petit b 132 77 55 33 22 11 77 55 22 22 11 11 a - b 55 22 33 11 11 0 Donc PGCD (132 ; 77) = 11

Recherche du PGCD de 132 et 77 Plus grand a Plus petit b 132 77 55 22 11 Reste 55 22 11 0 Donc PGCD (132 ; 77) = 11

132 Rendre irréductible la fraction 77 PGCD (132 ; 77) = 11 132 par 11 On simplifie 77 132 = 11 12 12 = 77 11 7 7

Propriété Lorsque l’on simplifie une fraction par le Plus Grand Commun Diviseur à son numérateur a et son dénominateur b la fraction obtenue est irréductible.

Nombres premiers entre eux

Définition : On dit que deux nombres a et b sont premiers entre eux lorsque leur Plus Grand Commun Diviseur est égal à 1 ; c’est à dire PGCD (a ; b) = 1 Cherchez deux nombres simples premiers entre eux

Définition : On dit qu’une fraction est irréductible lorsque son numérateur a et son dénominateur b sont premiers entre eux.

Fin

Alexandrie