Shell Structure of Nuclei and Cold Atomic Gases





![Super-shell structure predicted for repulsive interaction[1] g=0. 2 g=0. 4 g=2 Two close-lying frequencies Super-shell structure predicted for repulsive interaction[1] g=0. 2 g=0. 4 g=2 Two close-lying frequencies](https://slidetodoc.com/presentation_image_h2/8b293537652fea065daedace4391d9ca/image-8.jpg)
![II. Shell structure of BCS pairing gap [1] S. Åberg, H. Olofsson and P. II. Shell structure of BCS pairing gap [1] S. Åberg, H. Olofsson and P.](https://slidetodoc.com/presentation_image_h2/8b293537652fea065daedace4391d9ca/image-9.jpg)





![III. a Cold Fermionic Atoms in 2 D Traps [1] N atoms of spin III. a Cold Fermionic Atoms in 2 D Traps [1] N atoms of spin](https://slidetodoc.com/presentation_image_h2/8b293537652fea065daedace4391d9ca/image-27.jpg)





- Slides: 54

Shell Structure of Nuclei and Cold Atomic Gases in Traps Sven Åberg, Lund University, Sweden From Femtoscience to Nanoscience: Nuclei, Quantum Dots, and Nanostructures July 20 - August 28, 2009

Shell Structure of Nuclei and Cold Atomic Gases in Traps I. Shell structure from mean field picture (a) Nuclear masses (ground-states) (b) Ground-states in cold gas of Fermionic atoms: supershell structure II. Shell structure of BCS pairing gap (a) Nuclear pairing gap from odd-even mass difference (b) Periodic-orbit description of pairing gap fluctuations - role of regular/chaotic dynamics (c) Applied to nuclear pairing gaps and to cold gases of Fermionic atoms III. Cold atomic gases in a trap – Solved by exact diagonalizations IV. V. (a) (b) Collaborators: Cold Fermionic atoms in 2 D traps: Pairing versus Hund’s rule Effective-interaction approach to interacting bosons Stephanie Reimann, Massimo Rontani, Patricio Leboeuf Henrik Olofsson/Urenholdt, Jeremi Armstrong, Matthias Brack, Jonas Christensson, Christian Forssén, Magnus Ögren, Marc Puig von Friesen, Yongle Yu,

I. Shell structure from mean field picture

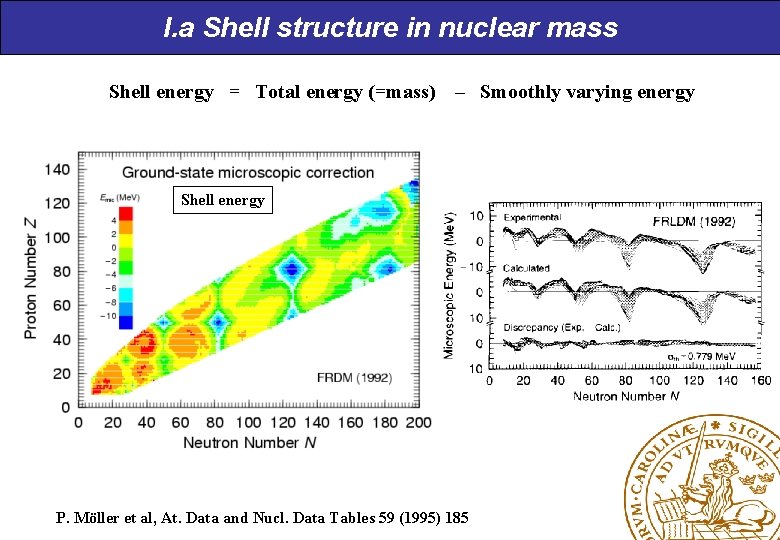
I. a Shell structure in nuclear mass Shell energy = Total energy (=mass) – Smoothly varying energy Shell energy P. Möller et al, At. Data and Nucl. Data Tables 59 (1995) 185

I. b Ground states of cold quantum gases Trapped quantum gases of bosonic or fermionic atoms: T 0 Bose condensate Degenerate fermi gas

Fermionic atoms in a 3 D H. O. confinement a = s-wave scattering length Un-polarized two-component system with two spin-states: Hartree-Fock approximation: Where: > 0 (repulsive int. )

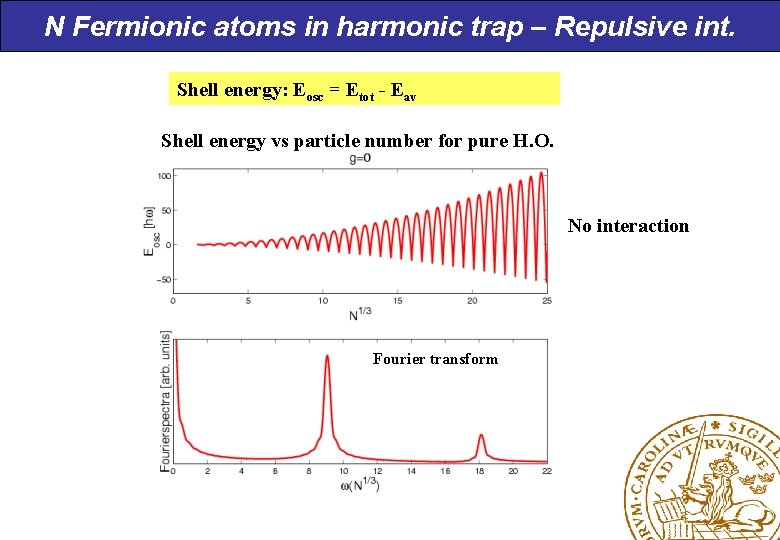
N Fermionic atoms in harmonic trap – Repulsive int. Shell energy: Eosc = Etot - Eav Shell energy vs particle number for pure H. O. No interaction Fourier transform
![Supershell structure predicted for repulsive interaction1 g0 2 g0 4 g2 Two closelying frequencies Super-shell structure predicted for repulsive interaction[1] g=0. 2 g=0. 4 g=2 Two close-lying frequencies](https://slidetodoc.com/presentation_image_h2/8b293537652fea065daedace4391d9ca/image-8.jpg)
Super-shell structure predicted for repulsive interaction[1] g=0. 2 g=0. 4 g=2 Two close-lying frequencies give rise to the beating pattern: circle and diameter periodic orbits Effective potential: [1] Y. Yu, M. Ögren, S. Åberg, S. M. Reimann, M. Brack, PRA 72, 051602 (2005)
![II Shell structure of BCS pairing gap 1 S Åberg H Olofsson and P II. Shell structure of BCS pairing gap [1] S. Åberg, H. Olofsson and P.](https://slidetodoc.com/presentation_image_h2/8b293537652fea065daedace4391d9ca/image-9.jpg)
II. Shell structure of BCS pairing gap [1] S. Åberg, H. Olofsson and P. Leboeuf, AIP Conf Proc Vol. 995 (2008) 173.

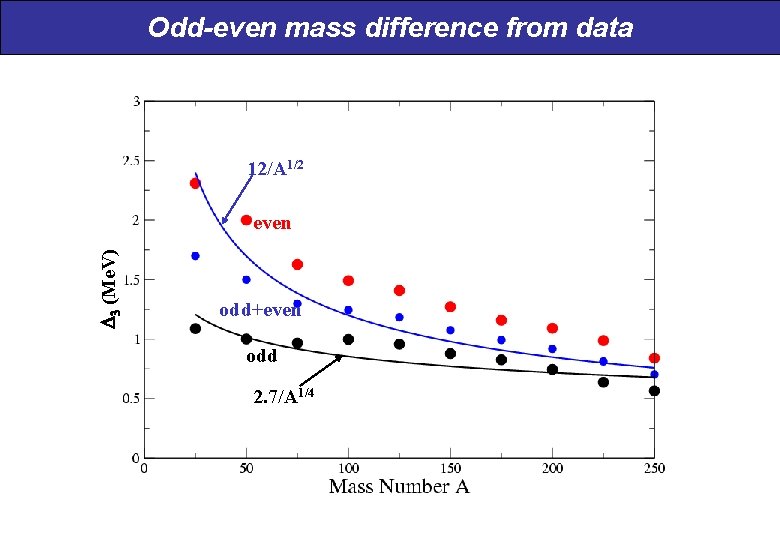
I. Odd-even mass difference Extraction of pairing contribution from masses: where 3(N even) = + de/2 3(N odd) = If no pairing: N=odd l is s. p. level density N=even de . . . 2 3(N) = 0 l odd N de. . . 2 3(N) = de W. Satula, J. Dobaczewski and W. Nazarewicz, PRL 81 (1998) 3599 even N

Odd-even mass difference from data 12/A 1/2 3 (Me. V) even odd+even odd 2. 7/A 1/4

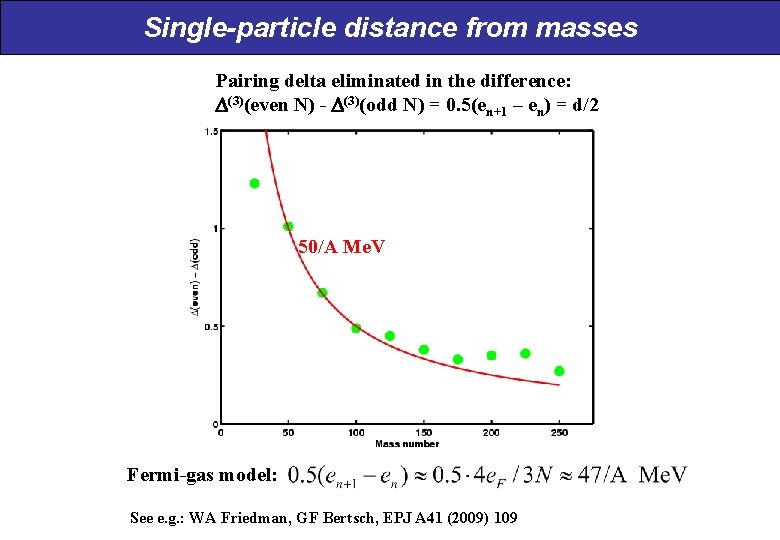
Single-particle distance from masses Pairing delta eliminated in the difference: (3)(even N) - (3)(odd N) = 0. 5(en+1 – en) = d/2 50/A Me. V Fermi-gas model: See e. g. : WA Friedman, GF Bertsch, EPJ A 41 (2009) 109

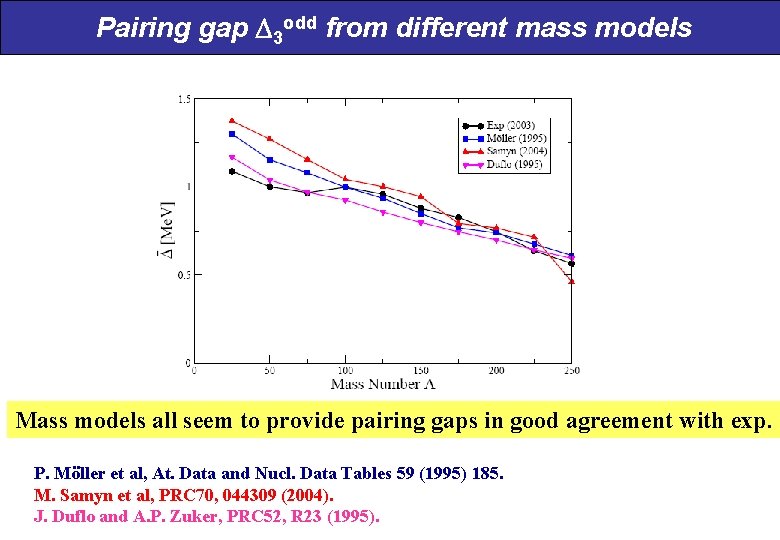
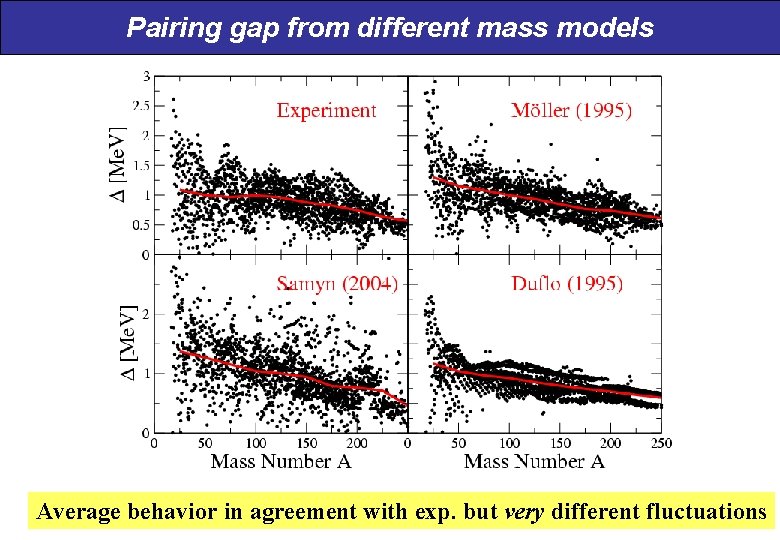
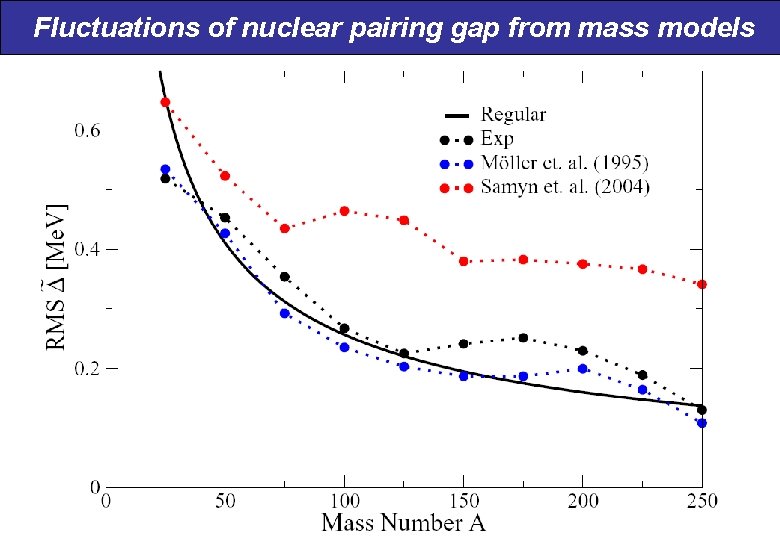
Pairing gap 3 odd from different mass models Mass models all seem to provide pairing gaps in good agreement with exp. P. Möller et al, At. Data and Nucl. Data Tables 59 (1995) 185. M. Samyn et al, PRC 70, 044309 (2004). J. Duflo and A. P. Zuker, PRC 52, R 23 (1995).

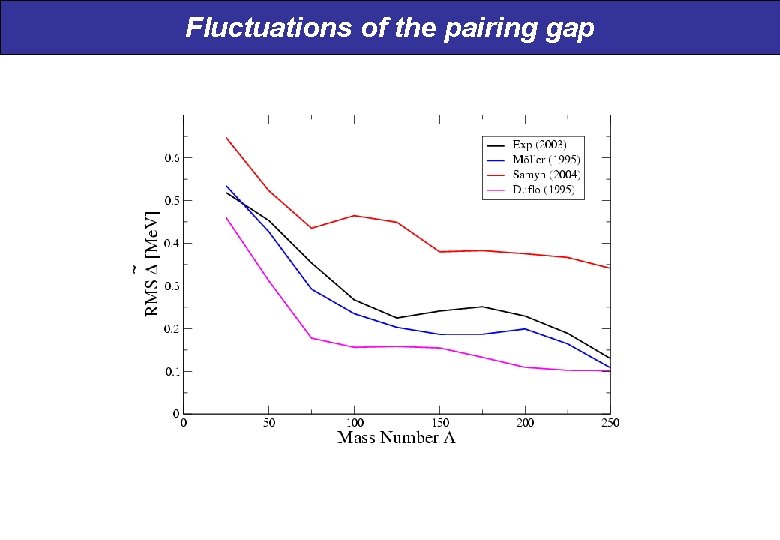
Pairing gap from different mass models Average behavior in agreement with exp. but very different fluctuations

Fluctuations of the pairing gap

II. b Periodic orbit description of BCS pairing Role of regular and chaotic dynamics [1] H. Olofsson, S. Åberg and P. Leboeuf, Phys. Rev. Lett. 100, 037005 (2008)

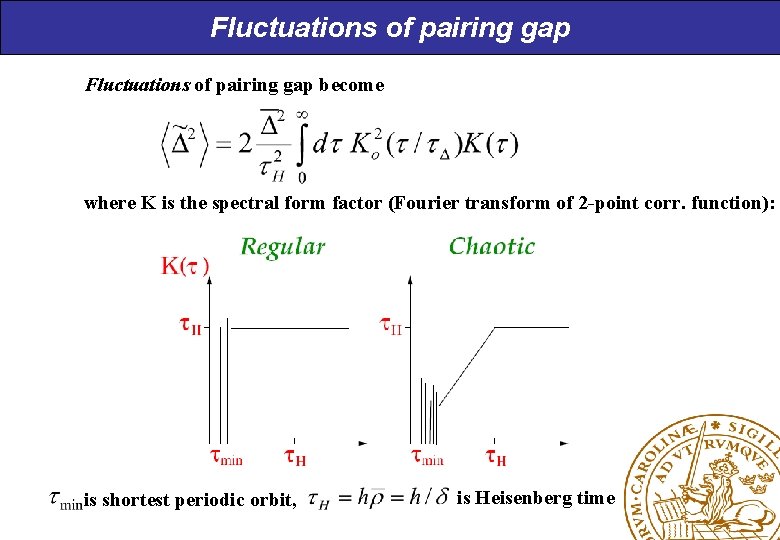
Periodic orbit description of pairing Pairing gap equation: Level density Insert semiclassical expression Divide pairing gap in smooth and fluctuating parts: Expansion in fluctuating parts gives: where is ”pairing time”

Fluctuations of pairing gap become where K is the spectral form factor (Fourier transform of 2 -point corr. function): is shortest periodic orbit, is Heisenberg time

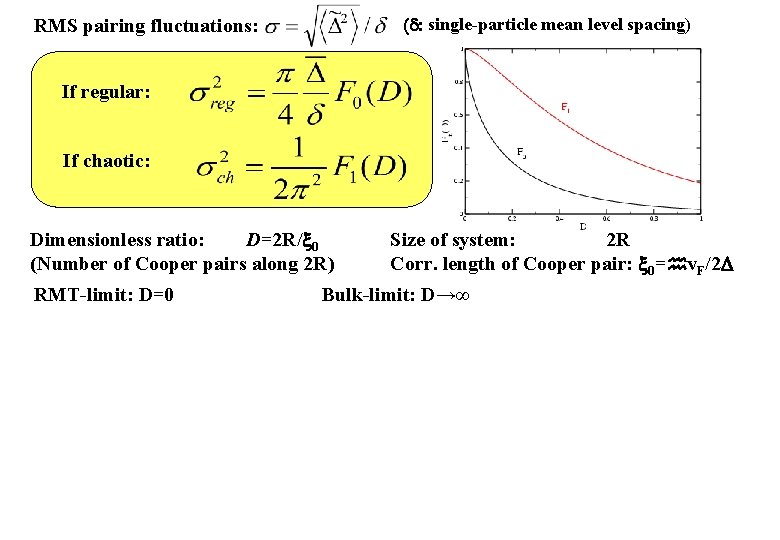
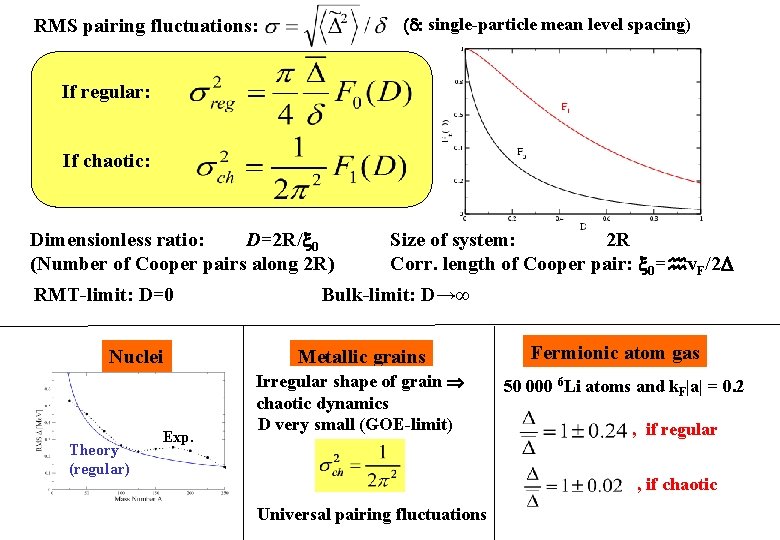
(d: single-particle mean level spacing) RMS pairing fluctuations: If regular: If chaotic: Dimensionless ratio: D=2 R/ 0 (Number of Cooper pairs along 2 R) RMT-limit: D=0 Size of system: 2 R Corr. length of Cooper pair: 0= v. F/2 Bulk-limit: D→∞

Universal/non-universal fluctuations ”dimensionless conductance” Non-universal spectrum fluctuations for energy distances larger than g: 3 statistics non-universal g=Lmax Random matrix limit: g (i. e. D = 0) corresponding to pure GOE spectrum (chaotic) or pure Poisson spectrum (regular)

(d: single-particle mean level spacing) RMS pairing fluctuations: If regular: If chaotic: Dimensionless ratio: D=2 R/ 0 (Number of Cooper pairs along 2 R) RMT-limit: D=0 Nuclei Theory (regular) Exp. Size of system: 2 R Corr. length of Cooper pair: 0= v. F/2 Bulk-limit: D→∞ Metallic grains Irregular shape of grain chaotic dynamics D very small (GOE-limit) Fermionic atom gas 50 000 6 Li atoms and k. F|a| = 0. 2 , if regular , if chaotic Universal pairing fluctuations

Fluctuations of nuclear pairing gap from mass models

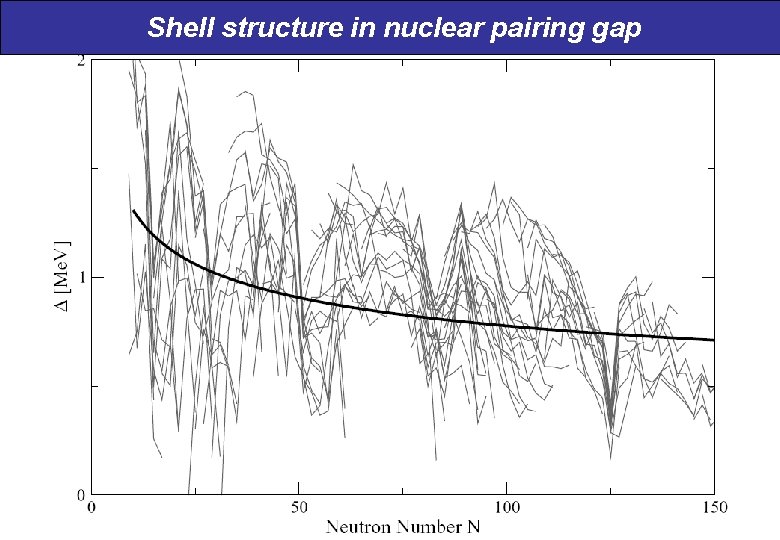
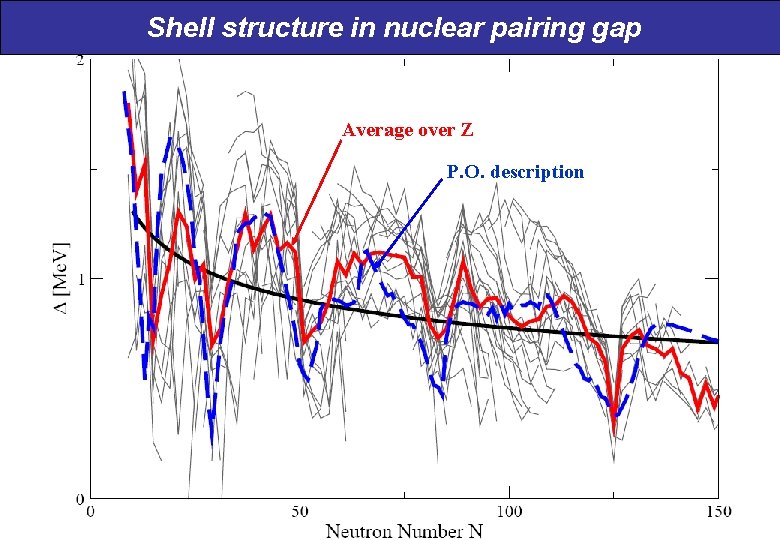
Shell structure in nuclear pairing gap

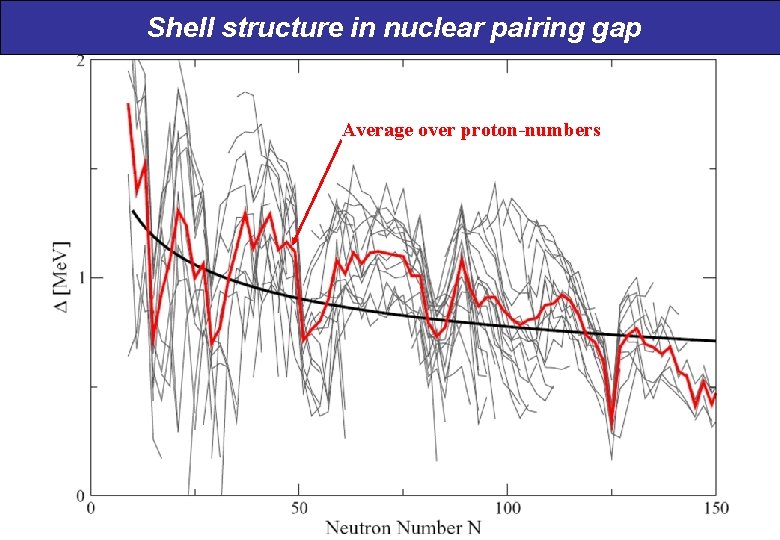
Shell structure in nuclear pairing gap Average over proton-numbers

Shell structure in nuclear pairing gap Average over Z P. O. description

III. Cold atomic gases in 2 D traps - Exact diagonalizations
![III a Cold Fermionic Atoms in 2 D Traps 1 N atoms of spin III. a Cold Fermionic Atoms in 2 D Traps [1] N atoms of spin](https://slidetodoc.com/presentation_image_h2/8b293537652fea065daedace4391d9ca/image-27.jpg)
III. a Cold Fermionic Atoms in 2 D Traps [1] N atoms of spin ½ and equal masses m confined in 2 D harmonic trap, interacting through a contact potential: Energy scale: Length scale: Dimensionless coupling const. : Contact force regularized by energy cut-off [2]. Energy (and w. f. ) of 2 -body state relates strength g to scattering length a. Solve many-body S. E. by full diagonalization ÞGround-state energy and excitated states obtained for all angular momenta attractive repulsive [1] M. Rontani, JR Armstrong, Y, Yu, S. Åberg, SM Reimann, PRL 102 (2009) 060401. [2] M. Rontani, S. Åberg, SM Reimann, ar. Xiv: 0810. 4305

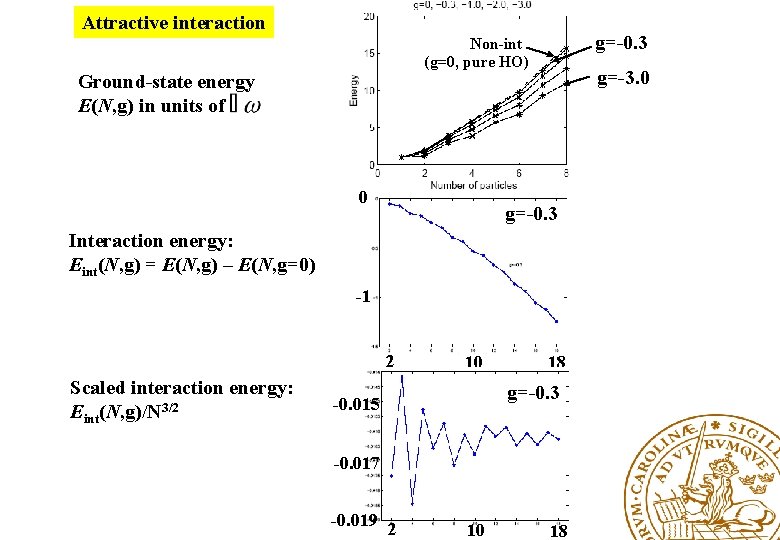
Attractive interaction g=-0. 3 Non-int (g=0, pure HO) Ground-state energy E(N, g) in units of 0 g=-3. 0 g=-0. 3 Interaction energy: Eint(N, g) = E(N, g) – E(N, g=0) -1 2 Scaled interaction energy: Eint(N, g)/N 3/2 10 18 g=-0. 3 -0. 015 -0. 017 -0. 019 2 10 18

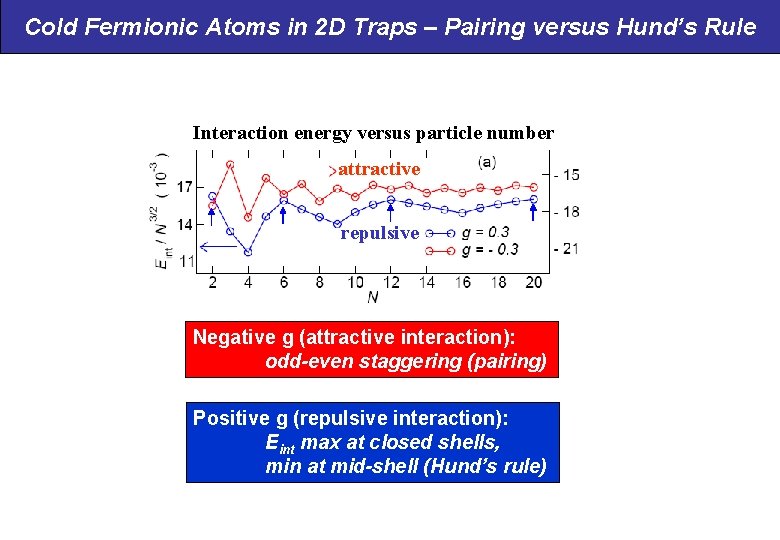
Cold Fermionic Atoms in 2 D Traps – Pairing versus Hund’s Rule Interaction energy versus particle number attractive repulsive Negative g (attractive interaction): odd-even staggering (pairing) Positive g (repulsive interaction): Eint max at closed shells, min at mid-shell (Hund’s rule)

Coulomb blockade – interaction blockade Coulomb blockade: Extra (electric) energy, EC, for a single electron to tunnel to a quantum dot with N electrons Difference between conductance peaks: where de is energy distance between s. p. states N and N+1 and E(N) total energy Interaction (or van der Waals) blockade [1]: Add an atom to a cold atomic gas in a trap Attractive interaction Repulsive interaction No interaction g=0. 3 1. 0 3. 0 5. 0 g=-0. 3 -1. 0 -3. 0 -5. 0 22 1 2 3 4 NN 5 6 Pairing Cheinetgap: et al, PRL 101 (2008) 090404 7 [1] C. Capelle et al PRL 99 (2007) 010402

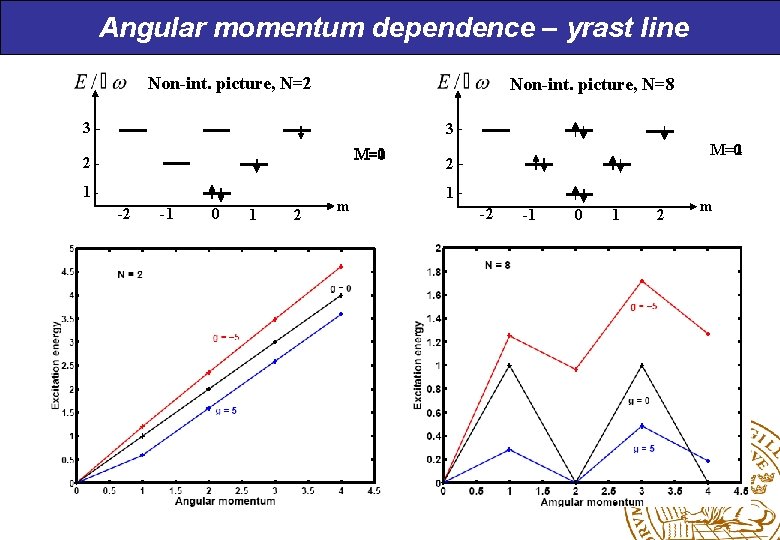
Angular momentum dependence – yrast line Non-int. picture, N=2 Non-int. picture, N=8 3 3 M=1 M=2 M=0 2 1 -2 -1 0 1 2 m M=0 M=2 M=1 2 1 -2 -1 0 1 2 m

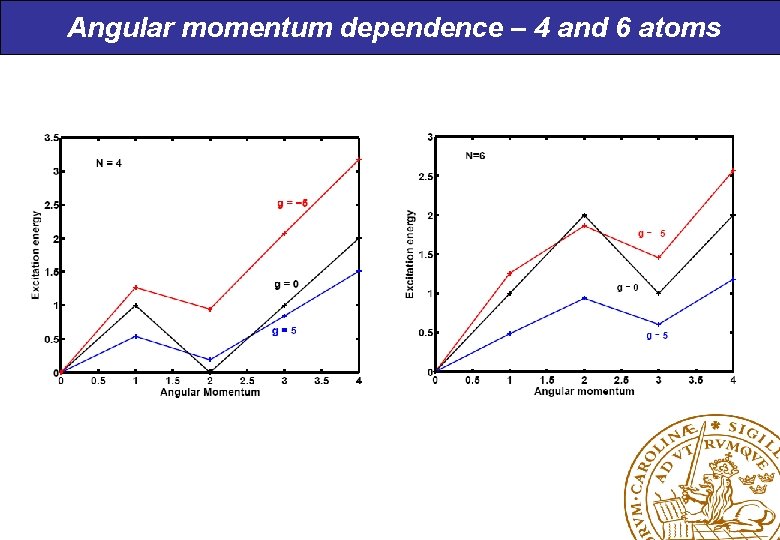
Angular momentum dependence – 4 and 6 atoms

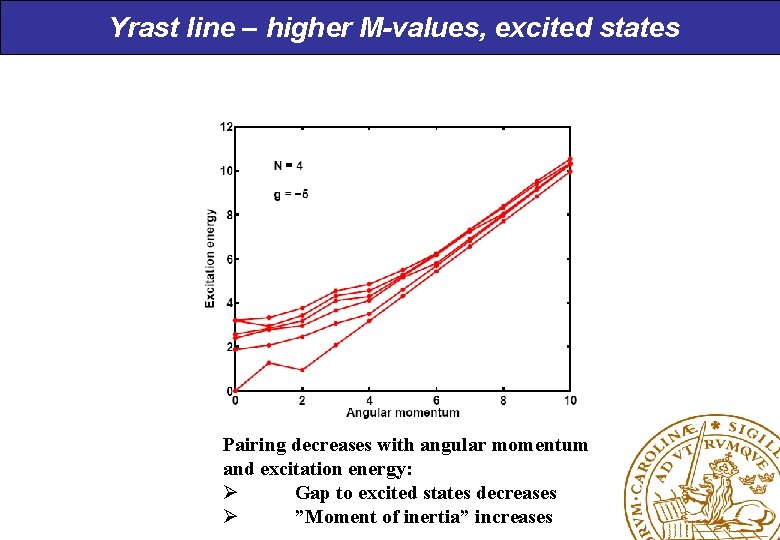
Yrast line – higher M-values, excited states Pairing decreases with angular momentum and excitation energy: Ø Gap to excited states decreases Ø ”Moment of inertia” increases

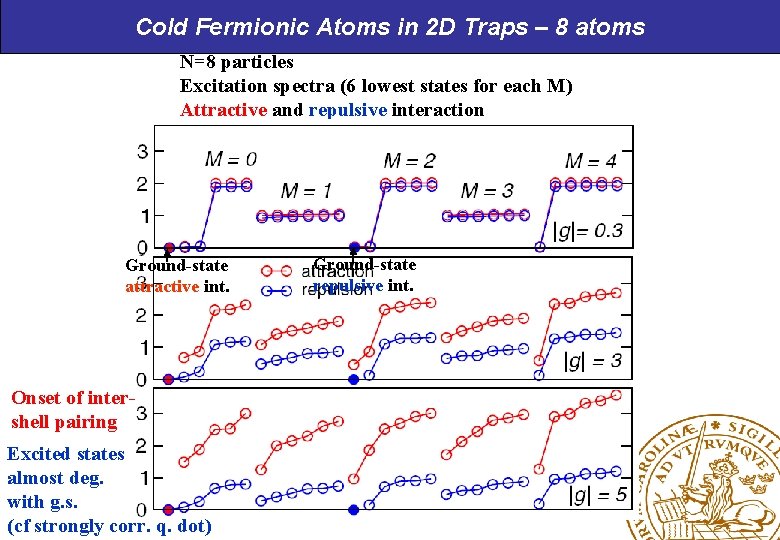
Cold Fermionic Atoms in 2 D Traps – 8 atoms N=8 particles Excitation spectra (6 lowest states for each M) Attractive and repulsive interaction Ground-state attractive int. Onset of intershell pairing Excited states almost deg. with g. s. (cf strongly corr. q. dot) Ground-state repulsive int.

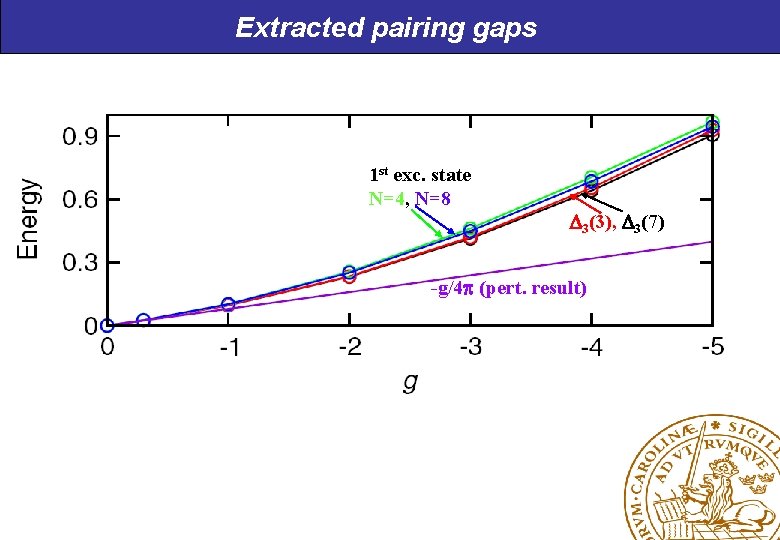
Extracted pairing gaps 1 st exc. state N=4, N=8 3(3), 3(7) -g/4 p (pert. result)

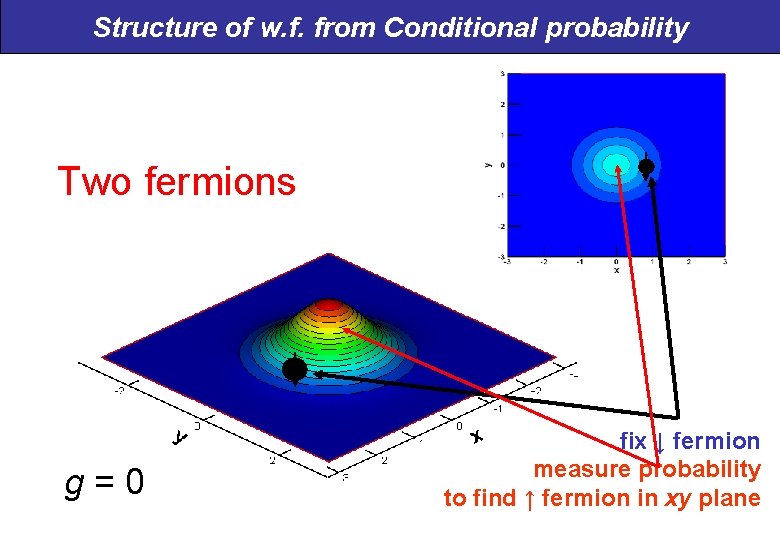
Structure of w. f. from Conditional probability Two fermions g=0 fix ↓ fermion measure probability to find ↑ fermion in xy plane

Two fermions g = - 0. 1

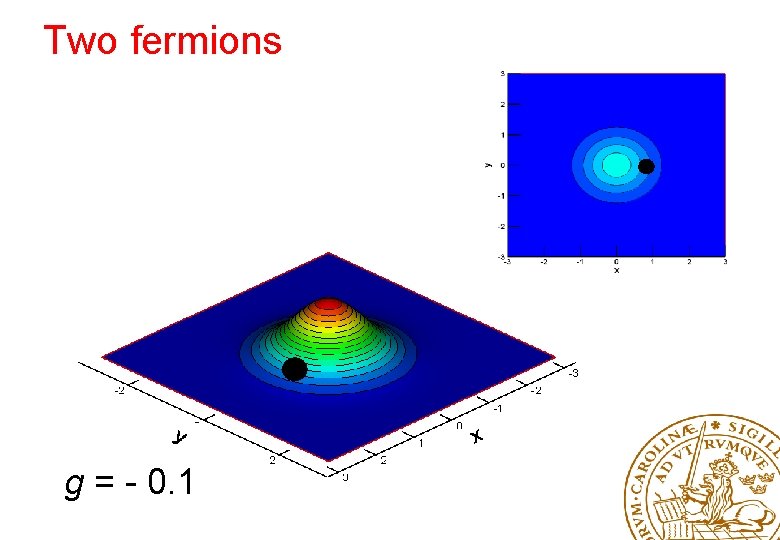
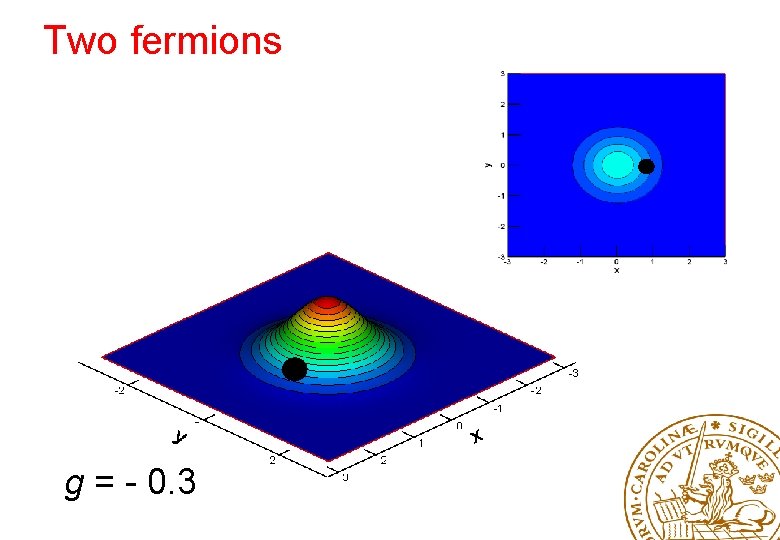
Two fermions g = - 0. 3

Two fermions g = - 0. 6

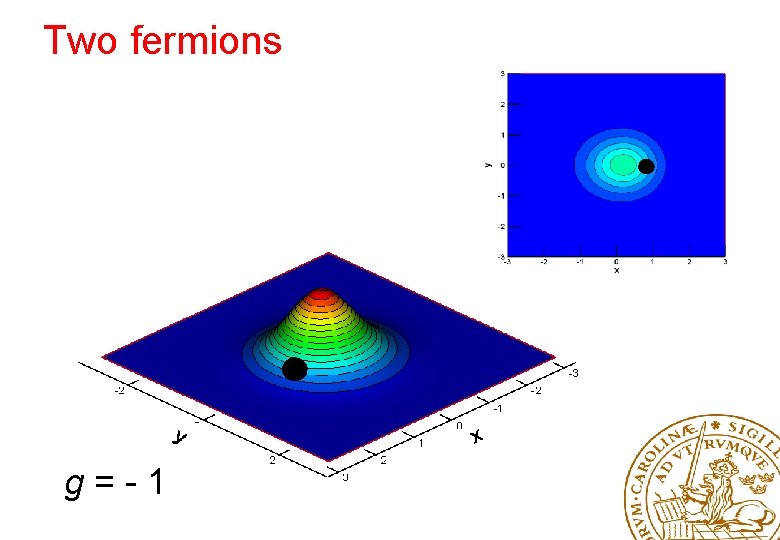
Two fermions g=-1

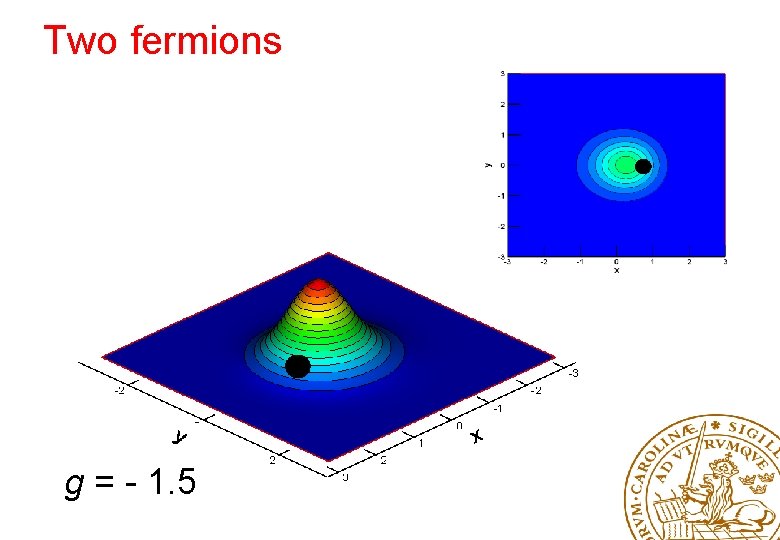
Two fermions g = - 1. 5

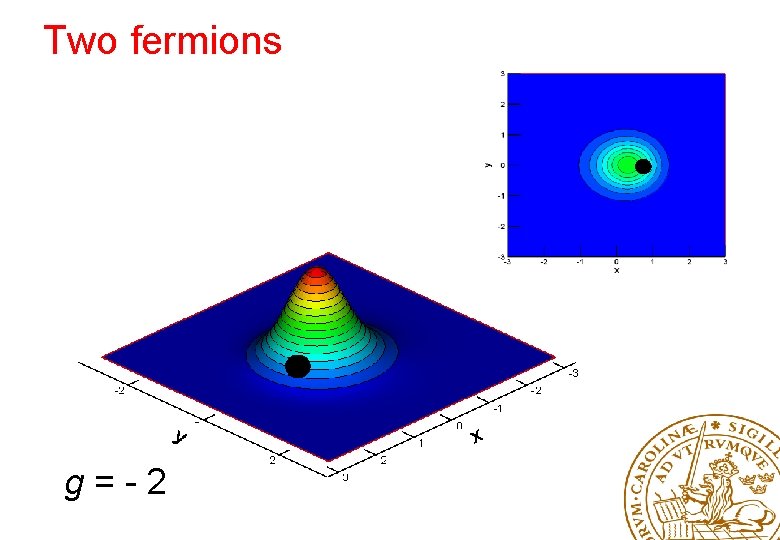
Two fermions g=-2

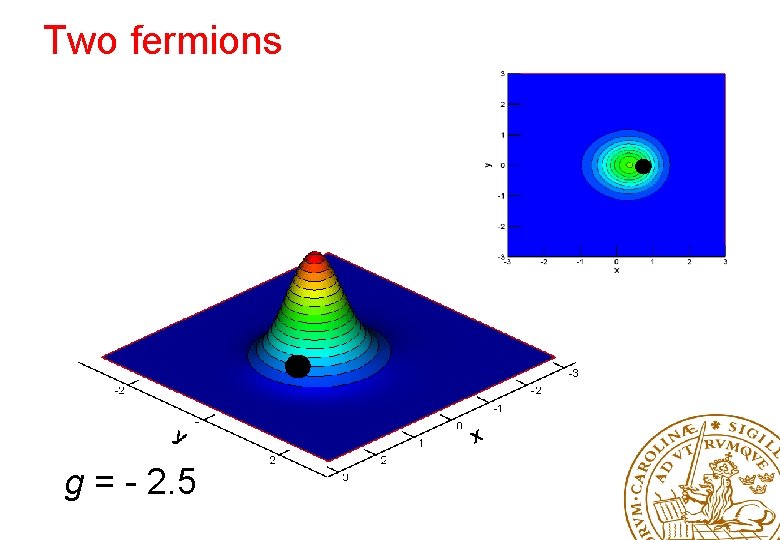
Two fermions g = - 2. 5

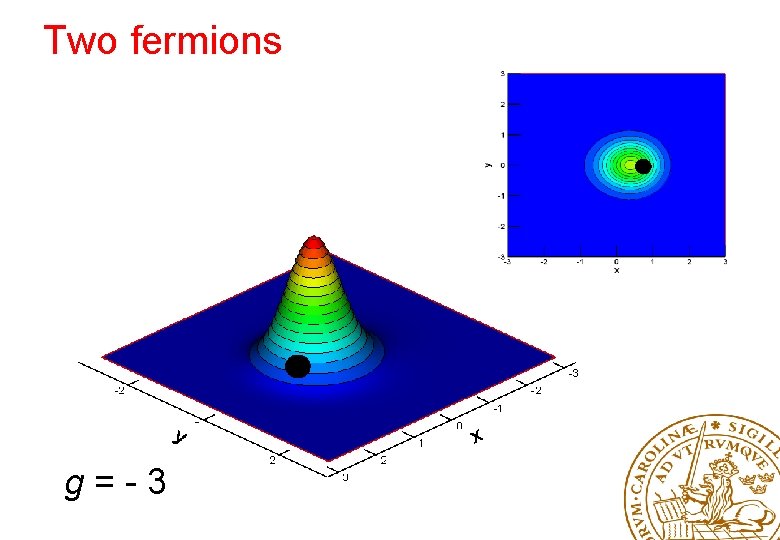
Two fermions g=-3

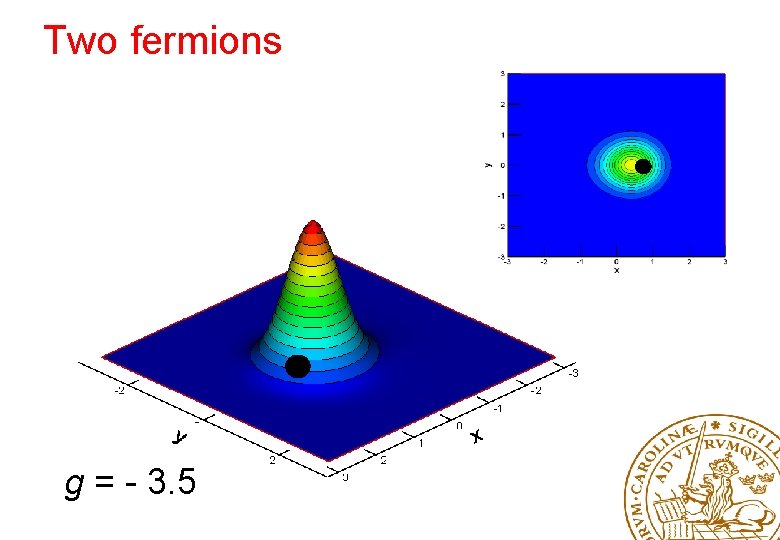
Two fermions g = - 3. 5

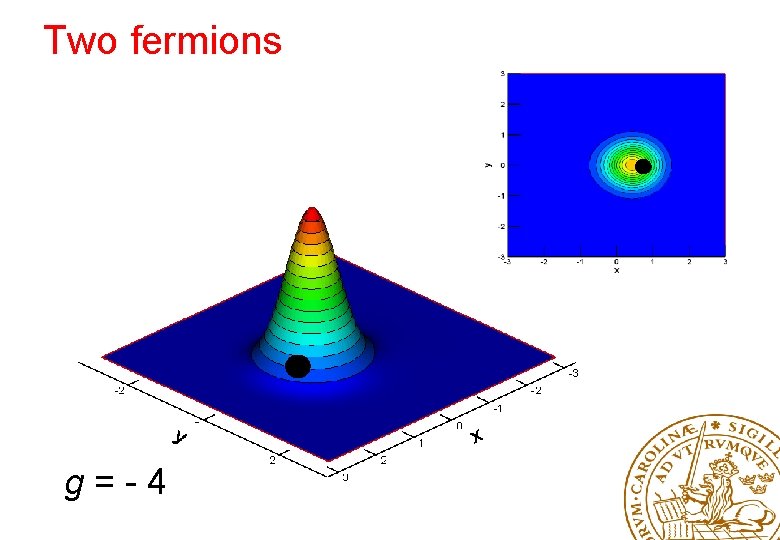
Two fermions g=-4

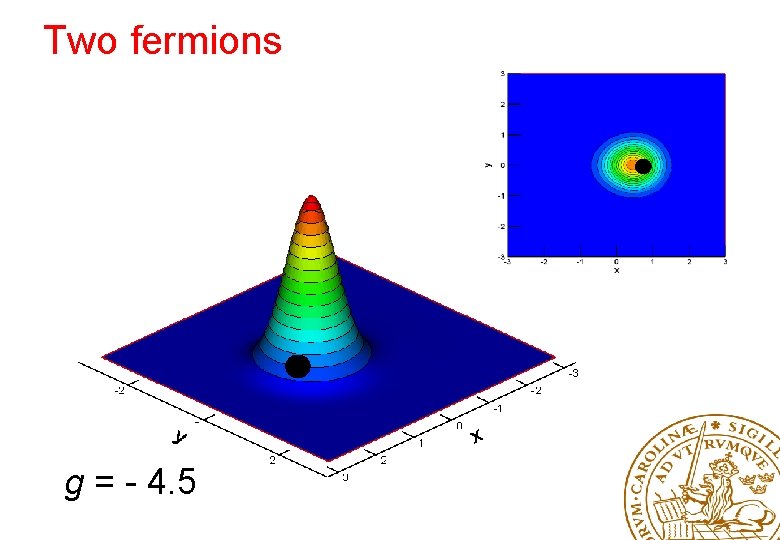
Two fermions g = - 4. 5

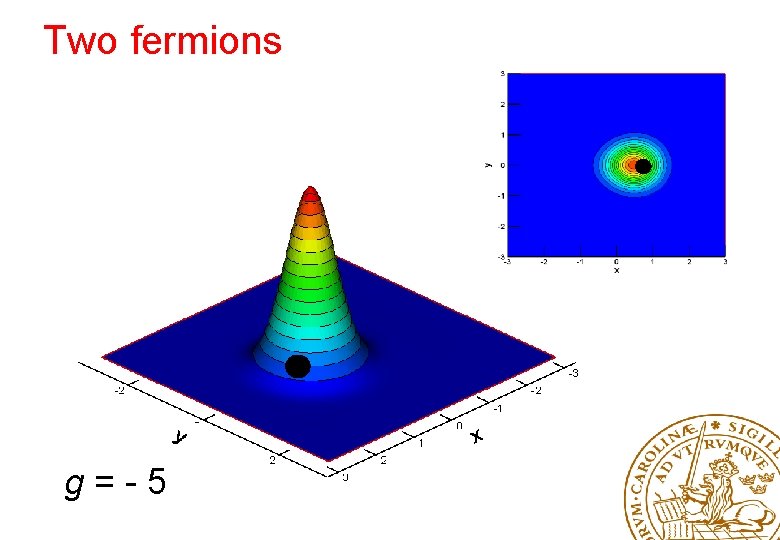
Two fermions g=-5

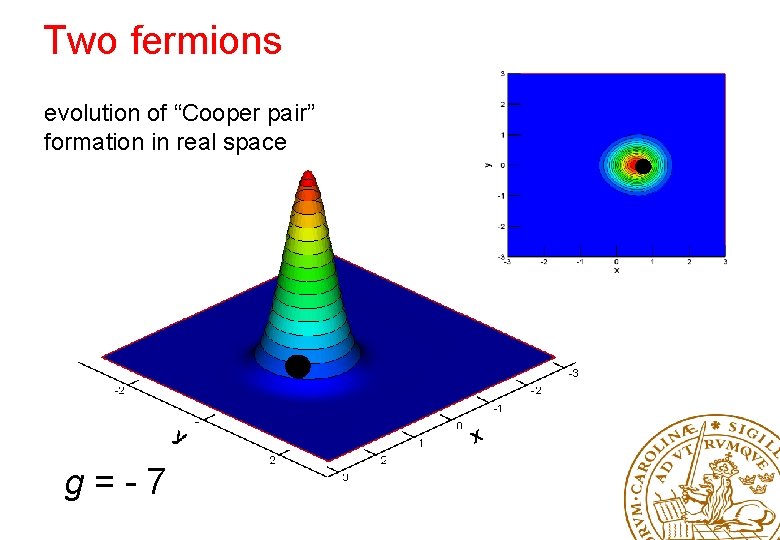
Two fermions evolution of “Cooper pair” formation in real space g=-7

Conditional probability distr. Repulsive interaction Attractive interaction

III. b Effective interaction approach to the many-boson problem N spin-less bosons confined in quasi-2 D Harmonic-oscillator Interact via (short-ranged) Gaussian interaction Range: s Strength: g g → 0 implies interaction becomes d-function Form all properly symmetrized many-body wave-functions (permanents) with energy: Energy of non-interacting ground-state: maximal energy of included states

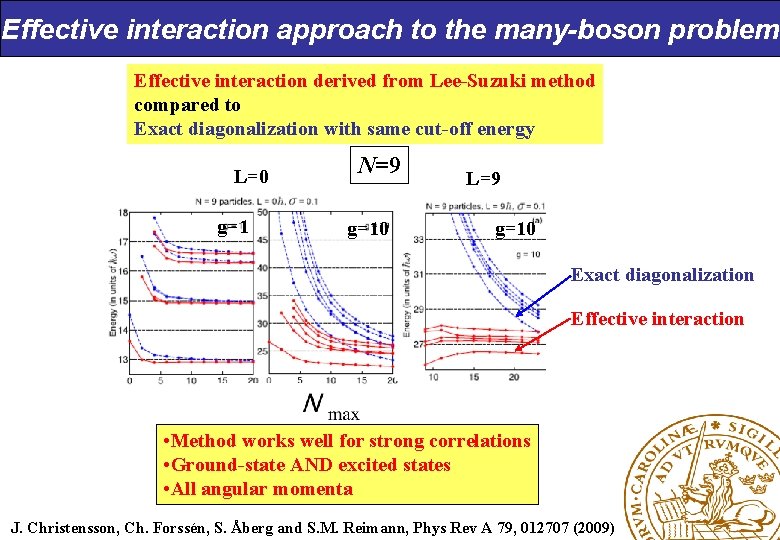
Effective interaction approach to the many-boson problem Effective interaction derived from Lee-Suzuki method compared to Exact diagonalization with same cut-off energy L=0 g=1 N=9 g=10 L=9 g=10 Exact diagonalization Effective interaction • Method works well for strong correlations • Ground-state AND excited states • All angular momenta J. Christensson, Ch. Forssén, S. Åberg and S. M. Reimann, Phys Rev A 79, 012707 (2009)

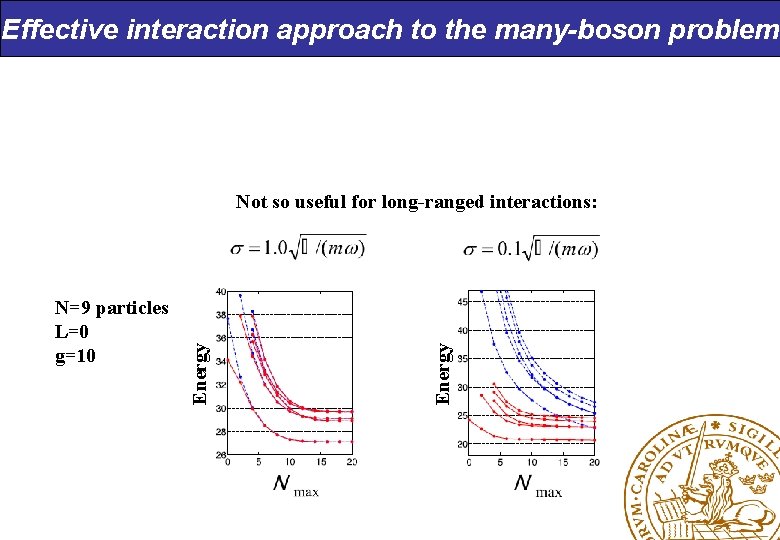
Effective interaction approach to the many-boson problem Energy N=9 particles L=0 g=10 Energy Not so useful for long-ranged interactions:

SUMMARY I. Cold Fermionic gases show supershell structure in harmonic confinement. II. Fluctuations and shell structure of BCS gaps in nuclei well described by periodic orbit theory. Non-universal corrections to BCS fluctuations important (beyond RMT). III. Cold Fermi-gas in 2 D traps - Detailed shell structure: Hund’s rule for repulsive int. ; Pairing type for attractive int. IV. V. Pairing from: Odd-even energy difference, 1 st excited state in even-N system, Cond. prob. function Interaction blockade. Yrast line spectrum VI. Effective interaction scheme (Lee-Suzuki) works well for many-body boson system (short-ranged force)
 Firmness of the yolk and freedom from yolk defects
Firmness of the yolk and freedom from yolk defects Shell cleanliness shell soundness shell
Shell cleanliness shell soundness shell Atomic nuclei
Atomic nuclei Relative atomic mass of beryllium
Relative atomic mass of beryllium O
O Atomic mass and atomic number difference
Atomic mass and atomic number difference Radius trend periodic table
Radius trend periodic table As atomic size
As atomic size Atomic number vs atomic radius
Atomic number vs atomic radius Cold vapor atomic fluorescence spectrometry
Cold vapor atomic fluorescence spectrometry Cold vapor atomic fluorescence spectrometry
Cold vapor atomic fluorescence spectrometry The cold war lesson 1
The cold war lesson 1 Noble gas lewis structure
Noble gas lewis structure Atomic structure and properties ap chemistry
Atomic structure and properties ap chemistry Ap chemistry atomic structure and periodicity
Ap chemistry atomic structure and periodicity Nonmetals are located where on the periodic table
Nonmetals are located where on the periodic table Apeman periodic table
Apeman periodic table Ap chemistry chapter 7 atomic structure and periodicity
Ap chemistry chapter 7 atomic structure and periodicity Interatomic bonding
Interatomic bonding Chapter 7 atomic structure and periodicity
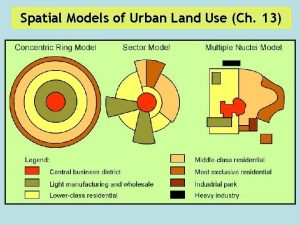
Chapter 7 atomic structure and periodicity Harris and ullman multiple nuclei model example
Harris and ullman multiple nuclei model example Sector model
Sector model Multiple nuclei model examples
Multiple nuclei model examples Harris ullman model
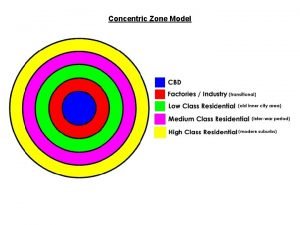
Harris ullman model Multiple zone model
Multiple zone model Harris and ullman multiple nuclei model
Harris and ullman multiple nuclei model Nmr active and inactive nuclei
Nmr active and inactive nuclei How unstable atoms gain stability
How unstable atoms gain stability Subatomic particles chart
Subatomic particles chart Atomic model diagram democritus
Atomic model diagram democritus Full bridge rectifier animation
Full bridge rectifier animation Ib chemistry atomic structure
Ib chemistry atomic structure Ib chemistry atomic structure
Ib chemistry atomic structure Atomic theory graphic organizer
Atomic theory graphic organizer Atomic theory model timeline
Atomic theory model timeline What is z in atomic structure
What is z in atomic structure Tungsten atomic structure
Tungsten atomic structure What scientist discovered the electron
What scientist discovered the electron Atoms poster
Atoms poster Atomic theory graphic organizer
Atomic theory graphic organizer Atomic model schrodinger
Atomic model schrodinger Dalton atom modeli
Dalton atom modeli Atomic structure webquest
Atomic structure webquest Volume to atoms
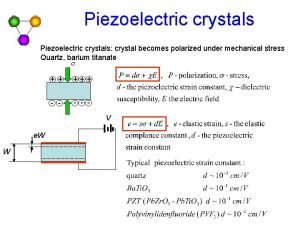
Volume to atoms Piezoelectric crystal atomic structure
Piezoelectric crystal atomic structure Boardworks atomic structure
Boardworks atomic structure Semiconductor atomic structure
Semiconductor atomic structure Chapter 4 atomic structure vocabulary
Chapter 4 atomic structure vocabulary Atomic structure
Atomic structure Atomic structure
Atomic structure Atomic structure of mg
Atomic structure of mg What is this
What is this Isotopes labeled
Isotopes labeled Discovery of atomic structure
Discovery of atomic structure What is a atom
What is a atom