Rataan Peubah Acak Variansi dan Kovariansi Rataan dan

Rataan Peubah Acak Variansi dan Kovariansi Rataan dan Variansi dari Kombinasi Linear Peubah Acak Teorema Chebyshev

Misalkan X suatu peubah acak dengan sebaran probabilitas f(x). Nilai rataan atau nilai harapan dari X adalah bila X diskrit, dan bila X kontinu.

Carilah nilai harapan banyaknya kimiawan dalam panitia 3 orang yang dipilih secara acak dari 4 kimiawan dan 3 biolog Jawab : Misalkan X menyatakan banyaknya kimiawan dalam panitia. Distribusi peluang X adalah… Beberapa perhitungan sederhana menghasilkan f(0) = 1/35, f(1) = 12/35 , f(2) = 18/35 dan f(3) =4/35

Jadi… Jadi, bila suatu panitia beranggota 3 orang dipilih secara acak berulang-ulang dari 4 kimiawan dan 3 biolog, maka ratanya akan beranggota 1, 7 kimiawan

Misalkan X merupakan peubah acak dengan sebaran probabilitas f(x). Nilai rataan atau nilai harapan peubah acak g(X) adalah jika X diskrit dan jika X kontinu.

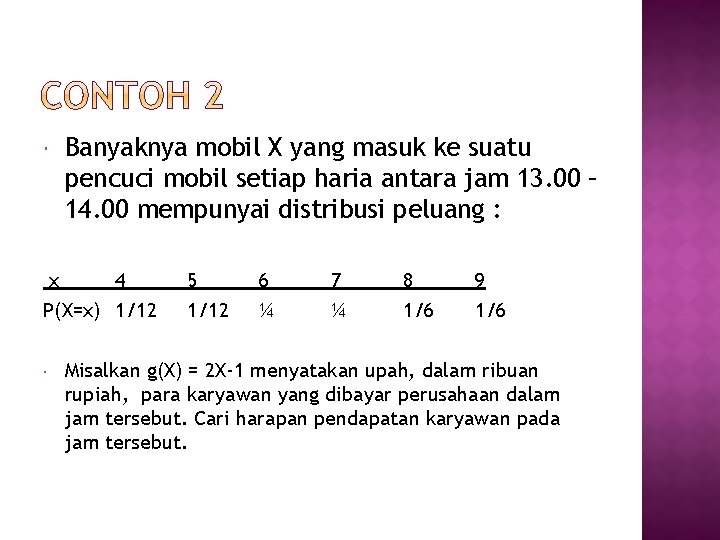
Banyaknya mobil X yang masuk ke suatu pencuci mobil setiap haria antara jam 13. 00 – 14. 00 mempunyai distribusi peluang : x 4 P(X=x) 1/12 5 1/12 6 ¼ 7 ¼ 8 1/6 9 1/6 Misalkan g(X) = 2 X-1 menyatakan upah, dalam ribuan rupiah, para karyawan yang dibayar perusahaan dalam jam tersebut. Cari harapan pendapatan karyawan pada jam tersebut.

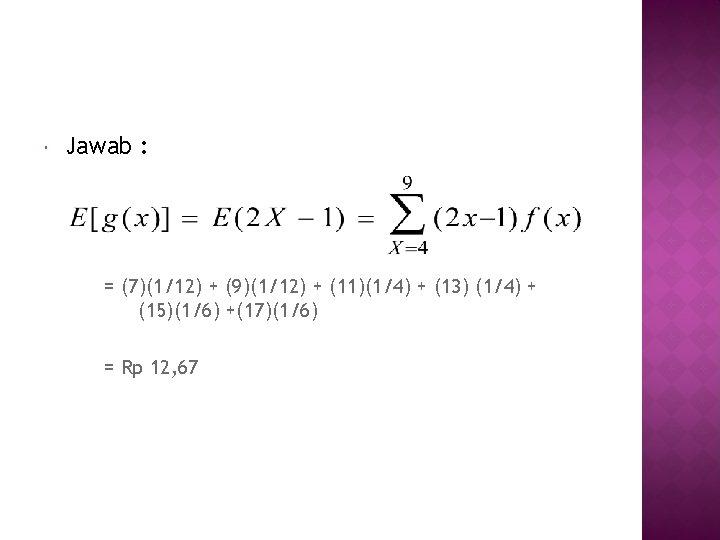
Jawab : = (7)(1/12) + (9)(1/12) + (11)(1/4) + (13) (1/4) + (15)(1/6) +(17)(1/6) = Rp 12, 67

Misalkan X dan Y merupakan peubah acak gabungan dengan sebaran probabilitas gabungan f(x, y). Nilai rataan atau nilai harapan peubah acak g(X, Y) adalah jika X dan Y diskrit, dan Bila X dan Y kontinu.

Misalkan X dan Y peubah acak dengan distribusi peluang gabungan pada Tabel 2. 6 hal 75. Hitunglah nilai harapan g(X, Y) = XY = (0) f(0, 0) + (0)(1)f(0, 1) + (0)(2)f(0, 2) + (1)(0) f (1, 0) + (1)(1) f(1, 1) + (2)(0) f(2, 0) = f(1, 1) = 3/14

Misalkan X merupakan suatu peubah acak dengan sebaran probabilitas f(x) dan nilai tengah µ. Ragam x adalah jika x diskrit, dan Jika X kontinu Akar kuadrat positif dari ragam, disebut simpangan baku X.

Misalkan peubah acak X menyatakan banyaknya mobil yang digunakan untuk keperluan dinas kantor pada setiap hari kerja. Distribusi peluang untuk kantor A adalah x 1 2 3 f(x) 0, 3 0, 4 0, 3 Dan untuk kantor B adalah x 0 1 2 3 4 f(x) 0, 2 0, 1 0, 3 0, 1 Tunjukkan bahwa variansi distribusi peluang kantor B lebih besar dari pada variansi kantor A

Jawab : Untuk kantor A diperoleh dan = (1 -2)2 (0, 3)+ (2 -2)2 (0, 3)+ (3 -2)2 (0, 3)=0, 6

Untuk kantor B diperoleh : Dan = (0 -2)2 (0, 2) + (1 -2)2 (0, 1) +(2 -2)2 (0, 3)+(3 -2)2 (0, 3) + (4 -2)2 (0, 1) =1, 6 Jelas. . variansi banyaknya mobil yang digunakan untuk Keperluan dinas lebih besar untuk kantor B daripada untuk kantor A. Rumus yang lebih mudah diberikan oleh teorema Berikut : Ragam peubah acak X adalah (Teorema 2)

Misalkan X merupakan sebuah peubah acak dengan sebaran probabilitas f(x). Ragam peubah acak g(X) adalah jika X diskrit jika X kontinu.

Misalkan X dan Y merupakan peubah acak dengan sebaran probabilitas gabungan f(x, y). variansi dari X dan Y adalah Jika X dan Y diskrit jika X dan Y kontinu

Peragam dari dua peubah acak X dan Y dengan nilai tengah masing-masing µX dan µY diberikan oleh

Jika a dan b merupakan konstanta, maka E(a. X+b) = a. E(X)+b akibat dari teorema di atas adalah: Dengan membuat a=0, kita lihat bahwa E(b)=0 § Dengan membuat b=0, kita lihat bahwa E(a. X)=a. E(X) §

Nilai harapan penjumlahan atau perbedaan dari dua atau lebih fungsi suatu peubah acak X adalah penjumlahan atau perbedaan dari nilai harapan fungsi itu. Dengan kata lain E[g(X)±h(X)] = E[g(X)]±E[h(X)] Nilai harapan dari penjumlahan atau perbedaan dua fungsi atau lebih dari peubah acak X dan Y merupakan penjumlahan atau perbedaan dari nilai harapan fungsi itu. Dengan kata lain E[g(X, Y)±h(X, Y)] = E[g(X, Y)]±E[h(X, Y)]

Akibat X dari teorema di atas adalah § Dengan membuat g(X, Y) = g(X) dan h(X, Y) = h(Y) kita lihat bahwa E[g(X)±h(Y)]=E[g(X)]±E[h(Y)] § Dengan membuat g(X, Y) = X dan h(X, Y) = Y, kita lihat bahwa E(X±Y) = E(X) ± E(Y) dan Y adalah dua peubah acak bebas, maka E(XY) = E(X)E(Y)

Jika a dan b merupakan konstanta maka Akibat dari teorema tersebut adalah § Dengan membuat a=1 § dengan membuat b=0

Jika X dan Y adalah peubah acak dengan sebaran probabilitas gabungan f(x, y) maka Akibat dari teorema tersebut adalah § Jika X dan Y adalah peubah acak bebas, maka § Jika X dan Y merupakan peubah acak bebas, maka

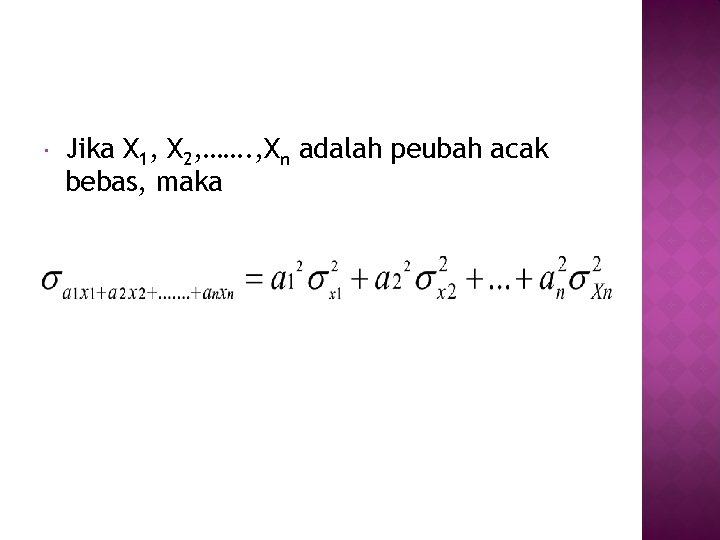
Jika X 1, X 2, ……. , Xn adalah peubah acak bebas, maka

Probabilitas bahwa setiap peubah acak X akan mengambil suatu nilai di dalam k simpangan baku dari nilai tengah paling sedikit adalah 1 -1/k² P(µ-kσ<X<µ+kσ)≥ 1 -1/k²

Suatu peubah acak X mempunyai rataan µ=8, variasi = 9, sedangkan peluang distribusinya tidak diketahui. Hitunglah a P(-4<X<20), dan b P( 6 ). Jawab : a. P(-4<X<20) = P[8 -(4)(3)<X<8+(4)(3)] 15/16 b. P( 6 ) = 1–P( < 6) = 1–P(-6 < X -8 < 6) = 1–P[8 -(2)(3)<X< 8+(2)(3)] 1/4