Potaov chemie 8 pednka vod 1 pednka Molekula

Počítačová chemie (8. přednáška) • Úvod (1. přednáška) • Molekula – Struktura molekuly (2. , 3. a 4. přednáška) – Geometrie molekuly (5. přednáška) – Vhled do praxe (6. přednáška) • Molekulové modelování – Molekulová mechanika (7. a 8. přednáška) – Kvantová mechanika (9. a 10. přednáška) – Molekulová dynamika (11. přednáška) – Vhled do praxe (12. přednáška)

Významné body v PES - matematické pojmy I Gradient: – Vektor prvních parciálních derivací funkce f v bodě x = (x 1, x 2, …, xn) – Označujeme ho Ñf(x): Chemický význam gradientu potenciálové funkce: Vektor síly v bodě x je roven -Ñf(x).

Významné body v PES - matematické pojmy II Hessian: – Matice druhých parciálních derivací funkce f v bodě x = (x 1, x 2, …, xn) – Označujeme ho Ñ 2 f(x) nebo také Hf(x)

Významné body v PES - matematické pojmy - cvičení Vypočítejte gradient a hessián Rosenbrockovy funkce (obecně a v bodě (1, 0)): f(x) = 100(x 2 – x 12)2 + (1 – x 1)2 Gradient: Hessián:

Domácí úkol 5 • Najděte free software (nebo shareware)*, který je schopen vypočítat Epot pro (alespoň 3) různá silová pole a napočítejte pomocí něho energii pro molekulu trans-2 -butenu (pdb soubor naleznete na www stránkách předmětu). (3%) • Vytvořte si molekulu 1, 1, 2 -trichlorethanu. Vyzkoušejte alespoň 5 různých torzních úhlů (Cl-C-C-H), a pro vzniklé konformery vypočítejte (např. pomocí programu Swis. PDBViewer) potenciální energii. Při odevzdávání přiložte soubory s konformery. (4%) *Neppočítám programy, které jsme si ukazovali na vhledu (viz slidz k vhledu).

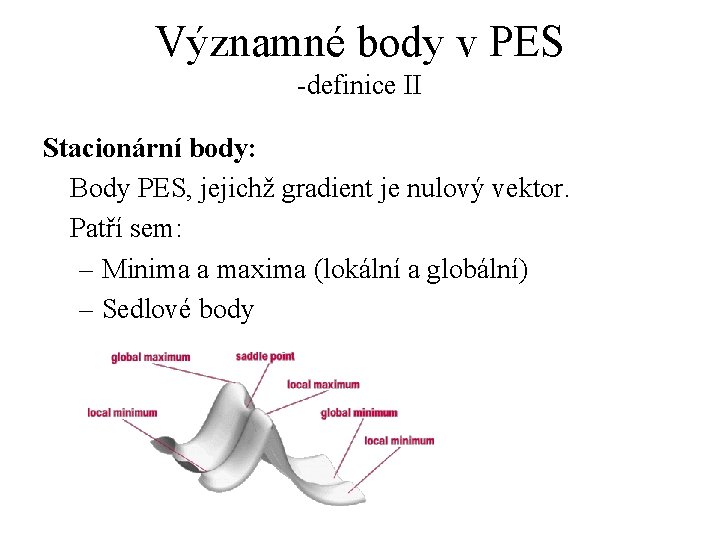
Významné body v PES -definice II Stacionární body: Body PES, jejichž gradient je nulový vektor. Patří sem: – Minima a maxima (lokální a globální) – Sedlové body

Významné body v PES -definice III Lokální minimum a lokální maximum (často se označuje pouze minimum a maximum): Minimum: $W "xÎW(x*): f(x) ³ f(x*) Maximum: $W "xÎW(x*): f(x) £ f(x*) Kde W(x*) je (vícerozměrné) okolí bodu x*.

Významné body v PES -definice IV Globální minimum: Pokud f(x) ³ f(x*) pro všechna x z definičního oboru funkce f, pak je x* globálním minimem funkce f. Obdobně je definováno globální maximum funkce f.

Významné body v PES -definice V Hessian a stacionární body: Minima*: Ve stacionárním bodě A funkce f je minimum, pokud jsou vlastní hodnoty hessianu Hf(A) kladná čísla. Maxima*: Ve stacionárním bodě A finkce f je maximum, pokud jsou vlastní hodnoty hessianu Hf(A) záporná čísla. *Jedná se o lokální minima a maxima. Dále budu vždy pod pojmem minimum nebo maximum mínit lokální minimum případně maximum.

Významné body v PES -definice VI Hessian a stacionární body: Pokud není stacionární bod ani minimum ani maximum, jedná se o sedlový bod. Speciálním typem sedlového bodu je tranzitní stav (= nejvyšší bod na nejkratším přechodu mezi dvěma minimy). Je to tedy v jednom rozměru maximum a v dalších rozměrech minimum. Má tedy jednu vlastní hodnotu hessianu zápornou a ostatní kladné.

Minima v PES -definice Chemický význam minim: Souřadnice, v nichž má PES minimum, popisují geometrii molekuly, která je v daném prostředí* stabilní. * Chemické prostředí je popsáno parametry silového pole.

Minima v PES - nalezení Pro vícerozměrné funkce zadané analyticky lze určit minima přímo z pomocí. Potenciálová funkce je zadána příliš složitým způsobem => nelze řešit analyticky => je nutno použít numerické metody

Minima v PES - nalezení II Problém minimalizace: Neformální definice: Pro bod A Î PES nalezněte nejbližší minimum, do kterého lze z bodu A sestoupit.

Minima v PES - nalezení III Problém minimalizace: Formální definice: Pro bod A Î PES nalezněte bod M Î PES, tak aby platilo: – M je minimum PES – existuje křivka z A do M, v jejíchž bodech má Epot tím nižší hodnotu, čím blíže je příslušný bod k bodu M

Minima v PES - metody nalezení Nederivační Jednoduché metody Postupná optimalizace proměnných Systematické prohledávání Náhodnostní metoda Metoda alternujících proměnných Simplexová (Nelder-Meadova) metoda Derivační První derivace Metoda největšího spádu + další spádové metody Metoda konjugovaných gradientů Druhá derivace Newton-Raphsonova metoda Quasi-Newtonova metoda

Jednoduché metody - postupná optimalizace proměnných Jedna z nejstarších optimalizačních metod (označována také „naivní metoda“ : -). Princip: Nejdříve nalezne minimum první proměnné (hodnoty ostatních proměnných se nemění). Původní hodnotu této proměnné nahradí nově nalezenou hodnotou. Analogicky jsou optimalizovány další proměnné. Zhodnocení: Metoda je použitelná pouze v některých případech: funkce 2 nebo 3 proměnných + vhodný tvar funkce. V součastnosti se tato metoda již nevyužívá.

Jednoduché metody - systematické prohledávání Anglicky označována grid search. Princip: Rozdělí vícerozměrný prostor, nad kterým je funkce definována na části pomocí vícerozměrné mřížky. Vypočítá pro každou část funkční hodnoty. Projde všechny funkční hodnoty a nalezne nejmenší z nich. V některých implementacích této metody analogickým způsobem prohledá okolí minima, nalezeného v předchozím kroku atd.

Jednoduché metody - systematické prohledávání Zhodnocení: Výhody: Spolehlivá metoda. Dnes se využívá pro hledání globálních extrémů případně pro nalezení všech extrémů v určité oblasti. Nevýhody: Složitost q(P 1. P 2. . . PN), kde Pi je počet dílů mřížky pro i-tou proměnnou a N je rozměr prostoru, nad kterým je studovaná funkce definována.

Jednoduché metody - náhodnostní metoda Princip: V rámci každého kroku výpočtu je vypočítáno mnoho hodnot studované funkce pro náhodně vybrané hodnoty proměnných (tyto hodnoty jsou ovšem náhodně vybrány z určitého regionu). Poté je nalezena nejmenší hodnota funkce a ta se stane středem nového regionu (který má menší rozměry než původní region). Zhodnocení: Použitelné, ale pouze při dostatečně velkém počtu vypočítaných funkčnch hodnot v každém kroku. Nevýhodou je velká složitost metody.

Jednoduché metody - metoda alternujících proměnných Anglicky označována alternating variables method. Princip: V iteraci k (k = 1, 2, . . . , N*) se mění (je optimalizována) pouze proměnná xk, ostatní proměnné jsou ponechány. Poznámka: Proměnná xk je optimalizována např. tak, že jsou vypočítány hodnoty xk´ = xk+dx a xk² = xk-dx, poté hodnoty f(x 1, . . . , xk´, . . . , x. N) a f(x 1, . . . , xk², . . . , x. N), a pak je pro další iteraci za xk použito nejvhodnější z xk´ a xk². Po proběhnutí iterací 1. . . N, když jsou všechny hodnoty optimalizovány, se celý cyklus opakuje znovu (až do splnění podmínek minima). * N je dimenze prostoru, nad kterým je funkce definována.

Jednoduché metody - metoda alternujících proměnných II Zhodnocení: Výhody: Jednoduchá implementace. Rozumná složitost. Nevýhody: V některých případech je tato metoda velmi neefektivní. Postup optimalizace je v těchto případech charakterizován oscilačním průběhem (viz následující obrázek). Navíc je znám problém (viz Practical methods of optimization), pro který metoda chybně konverguje k sedlovému bodu.

Jednoduché metody - metoda alternujících proměnných III Příklad pomalé konvergence metody:

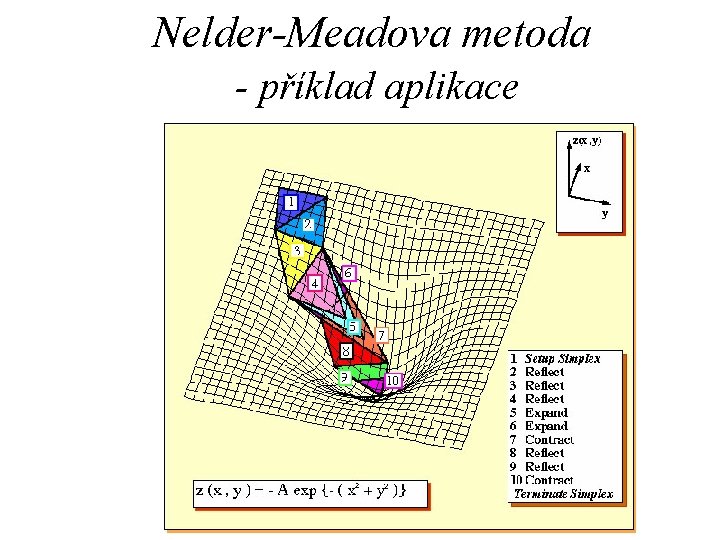
Nelder-Meadova metoda - obecně Nazývá se také simplexová metoda. Základní myšlenka: N-rozměrným prostorem se pohybuje jistý objekt („améba“), který se může natahovat nebo zkracovat v různých směrech. Několik typů takových transformací má zajistit, aby se objekt posouval směrem do „údolí“ a po dosažení dna údolí se „plazil“ co nejkratší cestou k lokálnímu minimu.

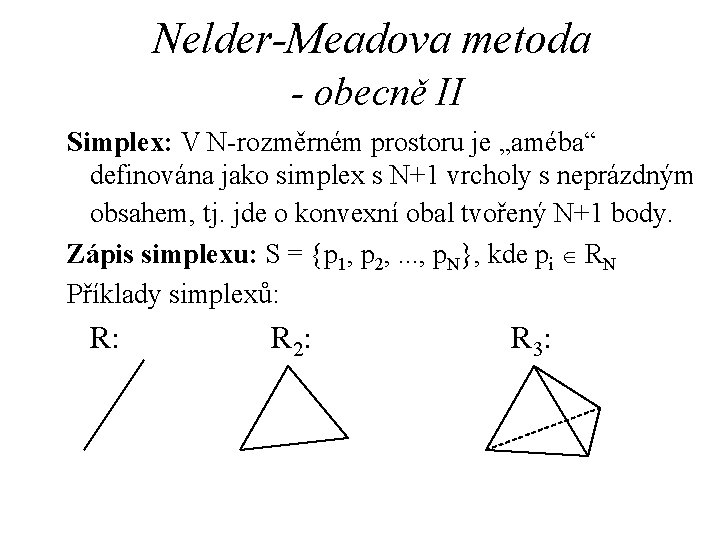
Nelder-Meadova metoda - obecně II Simplex: V N-rozměrném prostoru je „améba“ definována jako simplex s N+1 vrcholy s neprázdným obsahem, tj. jde o konvexní obal tvořený N+1 body. Zápis simplexu: S = {p 1, p 2, . . . , p. N}, kde pi Î RN Příklady simplexů: R 2: R 3:

Nelder-Meadova metoda - transformace Reflexe: Bod pi, který má největší funkční hodnotu se přemístí (odzrcadlí) na druhou stranu simplexu, tj. k bodu pi se přičte dvojnásobek rozdílu mezi pi a průměrem ostatních bodů.

Nelder-Meadova metoda - transformace II Reflexe a prodloužení: Totéž jako v předchozím případě, až na to, že simplex je prodloužen v novém směru (tj. přičítá se více než dvojnásobek rozdílu mezi nejhorším bodem a průměrem ostatních).

Nelder-Meadova metoda - transformace III Kontrakce: Nejhorší bod se přiblíží k průměru ostatních. To je vhodné v případě, kdy má „améba“ projít úzkým údolím.

Nelder-Meadova metoda - začátek výpočtu Na začátku výpočtu se simplex nejčastěji definuje takto: kde: i = 1, . . . , N p 0 pevně zvolený (počáteční) bod ei jednotkové vektory l konstanta, odrážející odhad měřítka optimalizačního problému (např. šířku „údolí“)

Nelder-Meadova metoda - ukončení výpočtu Metoda končí, pokud: – Není dosaženo výrazného snížení hodnoty studované funkce – simplex se v některém cyklu prakticky nezmění

Nelder-Meadova metoda - zhodnocení Výhody: – Jednoduchá implementace – Rychlý výpočet 1 iterace – Rychlá konvergence v oblastech daleko od minima Nevýhody: – Pomalá konvergence v oblasteh poblíž minima – Může nastat situace, že výpočet neskončí v lokálním minimu

Nelder-Meadova metoda - příklad aplikace

Metoda největšího spádu -obecně Anglicky označována steepest descent method. Princip: Vydat se směrem, ve kterém studovaná funkce nejrychleji klesá. Tedy ve směru Ñf(x), kde x je bod, ve kterém se výpoèet právì nachází. -

Metoda největšího spádu -obecně II Algoritmus: • zvolíme výchozí bod x(0) • k-tá iterace: bod x(k+1) vypočítáme z bodu x(k) pomocí vztahu: x(k+1) = x(k) - a. g(k), kde: -g(k) a zjednodušený zápis -Ñf(x(k)), určuje směr přesunu z bodu x(k) koeficient, popisující délku daného přesunu

Metoda největšího spádu - volba a v metodě největšího spádu Z bodu x(k) se přesunujeme po polopřímce: x(a) = x(k) + a. x(k), kde a > 0 Hodnotu funkce f na této polopøímce popisuje funkce f(a): f(a) = f(x(a)) Je zřejmé, že musíme zvolit takové a. OK, aby platilo: f(x(k)) > f(x(k+1)), kde x(k+1) = x(a. OK) pro dostatečný počet iterací. Poznámka: „Dostateèný počet“ = dostačuje k tomu, aby metoda konvergovala k minimu ( ).

Metoda největšího spádu zhodnocení Výhody: • Implementačnì jednoduché • Nízká prostorová složitost Nevýhody: • Velmi pomalá konvergence (speciálně v oblastech malého spádu => nízkých hodnot gradientu). • Chyby, způsobené zaokrouhlením. Mohou vést i k tomu, že se výpočet vůbec nedostane rozumně blízko k minimu. Ale při (ideální) přesné aritmetice metoda konverguje vždy k nějakému lokálnímu minimu.

Spádové metody - obecně Jsou založeny na stejném principu jako metoda největšího spádu: x(k+1) = x(k) + a(k). s(k), kde: s(k) a(k) je směr přesunu z bodu x(k), nejčastěji jako směr volíme -g(k) koeficient, popisující délku daného přesunu Využívají sofistikovanější metody k určení koeficientu a. Hodnota koeficientu a je různá pro každou iteraci.

Metody konjugovaných gradientů - obecně = metody sdružených gradientů = conjugate gradient method = speciální případ metod sdružených směrů Základní myšlenka: Pro určení směru přesunu z bodu x(k) do bodu x(k+1) se využívají nejen hodnotu g(k+1), ale rovněž hodnotu g(k). (V obecném případě je možno využít hodnot g(1), g(2), . . . , g(k), g(k+1). ) Zdůvodnění: Spojení informací o současném a předchozím sklonu studované funkce umožňuje rychlejší sestup do minima (zlepšení konvergence na plochých oblastech).

Metody konjugovaných gradientů - algoritmus Výpočet x(k+1): x(k+1) se určuje pomocí stejného vztahu jako u spádových metod: x(k+1) = x(k) + a(k). s(k) [2. 1] kde: s(k) a(k) směr přesunu z bodu x(k) koeficient, popisující délku daného přesunu

Metody konjugovaných gradientů - algoritmus II Výpočet s(k+1): s(k+1) se vypočte pomocí gradientu g(k+1) a směru s(k). (Přičemž s(k) byl vypočítán pomocí předchozích hodnot gradientů. . . ). Konkrétně: s(k+1) = -g(k+1) + b(k). s(k) [2. 2] Kde b(k) je koeficient, který určuje míru vlivu směru přesunu v kroku k (s(k)) na směr přesunu v následujícím kroku (s(k+1) ). Výpočet s(0): s(0) = -g(0)

Metody konjugovaných gradientů - algoritmus III Výpočet b(k+1): Existuje více možností, jak volit číslo b(k+1). – Hestenes a Stiefel (1952): – Polak a Ribiere (1969): – Fletcher a Reeves (1963):

Newtonovské metody - klasická Newtonova metoda Konstruuje x(k+1) přímo pomocí H(k). V k-ém kroku Newtonovy metody se pak provedou následující operace: a) Najdi řešení d(k) rovnice H(k). d(k) = -g(k) b) Polož x(k+1) = x(k) + d(k)

Newtonovské metody - klasická Newtonova metoda II Nejčastějším postupem, jak získat d(k) je tento: d(k) = - (H(k))-1. g(k) Pro x(k+1) tedy platí: x(k+1) = x(k) - (H(k))-1. g(k)

Newtonovské metody - klasická Newtonova metoda III Příklad: funkce: f(x, y) = x 2 + 2 y 2 bod: x(0) = (9, 9) gradient v bodě x(0): g(0) = (18, 36)T hessian v bodě x(0): inverzní hessian: bod x(1):

Minima v PES - Quasi-Newtonova metoda I Při využití Newton-Raphsonovy metody je nejvíce výpočetně náročné určení inverzního hessianu. Tento krok lze obejít a místo inverzního hessianu použít sérii matic, které se mu limitně blíží: Pro funkci f tedy platí: xk+1 = xk – H´k. gk kde: gk je gradient H´k je aproximace inverzního hessianu pro krok k výpočtu

Minima v PES - Quasi-Newtonova metoda II Pro výpočet aproximací inverzního hessianu se používají následující metody: • DFP (Davidon-Fletcher-Powell) • BFGS (Broyden-Fletcher-Goldfarb-Shanno) • MS (Murtaugh-Sargent) • Další DFP:

Tranzitní stavy v PES -definice Chemický význam tranzitních stavů: Mějme na PES dvě minima (jedno odpovídá molekule M 1 a druhé molekule M 2), pak tranzitní stav mezi M 1 a M 2 popisuje souřadnice aktivního komplexu pro reakci M 1 ® M 2. Neformální definice tranzitního stavu: Nejvyšší bod na nejkratším (energeticky nejméně náročném) přechodu mezi dvěma minimy. Formální definice tranzitního stavu: Bod A je tranzitním stavem PES, pokud je v tomto bodě gradient funkce f nulový, jedna vlastní hodnota hessiánu záporná a ostatní kladné.

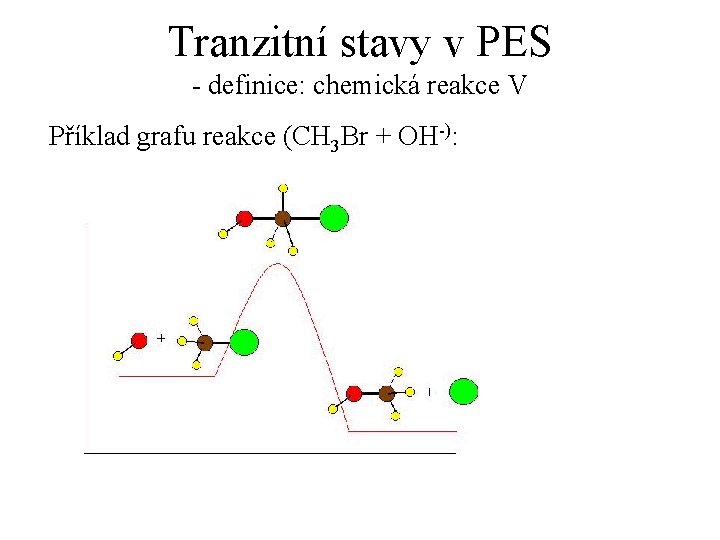
Tranzitní stavy v PES - definice: chemická reakce Chemická reakce: Děj, při němž některé vazby mezi atomy v molekulách výchozích látek zanikají a vytvářejí se nové vazby a tedy i molekuly nových látek - produktů reakce. Teorie aktivovaného komplexu: Popisuje chemickou reakci z energetického a geometrického hlediska.

Tranzitní stavy v PES - definice: chemická reakce II Reakční koordináta: Souřadnice, podél níž se zúčastněné částice při reakčním kroku „posunují“. Má též význam míry (procenta) uskutečnění daného elementárního děje. Graf reakce: Příklad reakčního schématu:

Tranzitní stavy v PES - definice: chemická reakce III Na počátku reakce jsou přítomny pouze reaktanty A a B. V průběhu reakce přicházejí molekuly A a B do kontaktu, mění se jejich prostorové uspořádání a začíná výměna nebo uvolňování atomu případně atomů. Postupně se formují nové vazby a zeslabují původní vazby, kterých se týká reakční změna. Potenciální energie roste, až dosáhne svého maxima.

Tranzitní stavy v PES - definice: chemická reakce IV Bod na reakční křivce, ve kterém je Epot maximální, se nazývá tranzitní stav. Molekulový systém, jehož souřadnice odpovídají energetickému maximu, se nazývá aktivní komplex. Poté se začínají původní vazby rozpadat a nové se zpevňují, tím se aktivní komplex přeměňuje na molekuly produktu. V průběhu tohoto procesu Epot klesá. Pro samovolné reakce platí: Epot(produktů) < Epot(reaktantů)

Tranzitní stavy v PES - definice: chemická reakce V Příklad grafu reakce (CH 3 Br + OH-):

Tranzitní stavy v PES - PES molekulového systému PES pro každý molekulový systém zároveň obsahuje informace i o všech molekulových systémech, izomerních s tímto molekulovým systémem. Pro každý systém s definovaným počtem elektronů a počtem a typem atomů existuje specifická PES.

Tranzitní stavy v PES - PES molekulového systému II Příklad: Systém, obsahující 2 atomy H a 2 elektrony Izomerní molekulové systémy (lokální minima PES): H, H+, e 2 H+, 2 e. H+, H 2 H H-H Globální minimum systému: H-H

Tranzitní stavy v PES - PES a chemická reakce Reaktanty a produkty chemické reakce jsou v rámci PES sousedními lokálními minimy. Reakční koordináta je v PES nejkratší cestou z minima, odpovídajícího reaktantům do minima, odpovídajícího produktům. V PES se označuje IRC (intrinsic reaction coordinate).

Tranzitní stavy v PES - PES a chemická reakce II Význam tranzitních stavů: Studium mechanizmu chemické reakce: – Struktura aktivního komplexu – Potenciální energie aktivního komplexu – Průběh reakční koordináty Nalezení reakčních cest mezi dvěma nesousedícími minimy

Tranzitní stavy v PES - vyhledávání Nejčastěji se používají tyto metody: – Linear synchronous transit (LST) – Quadratic synchronous transit (QST) – Saddle optimization method (SOM) – Locally updated planes (LUP) – Self penalty walk (SPW)

Tranzitní stavy v PES - vyhledávání II Všechny vyhledávací metody jsou založeny na předpokladu, že známe souřednice reaktantů (R) a produktů (P). Tranzitní stav (TS) je lokalizován „někde mezi“ R a P. Metody se liší pouze tím, jakou používají interpolaci. Linear synchronous transit (LST): Vytvoří úsečku z R do P. Vypočítá Epot pro některé body (= souřadnice atomů) této úsečky. Jako TS označí ten bod úsečky, pro který je hodnota Epot největší.

Tranzitní stavy v PES - vyhledávání III Quadratic synchronous transit (QST): Nejdříve pracuje stejně jako LST. Z bodů R, P a TS sestrojí parabolu. Na této parabole vyhledává opět maximum Epot (nový TS). Saddle optimization method (SOM): Vychází ze struktur P a R. Zkouší na základě R podle vzoru P vygenergovat mezistrukturu (s co největší Epot), která se velmi podobá R, ale obsahuje již malé strukturní změny směrem k P. Touto strukturou R 2 poté nahradí R. Analogicky nalezne pro P odpovídající P 2 a tím P nahradí. Opakuje tento proces až do splnění konvergenčních podmínek.

Tranzitní stavy v PES - vyhledávání IV Locally updated planes (LUP): Na spojnici R a P nalezne maximum a toto maximum relaxuje: Při relaxaci využívá kolmici k nadrovině nalezeném maximu. Self penalty walk (SPW): Reakční cesta je vyhledávána pomocí minimalizace průměrné energie podél dané cesty. Tato energie se vypočte ze vztahu: kde: L je celková délka cesty dl(x) je délkový element této cesty

Globální minimum v PES - definice a význam Definice: Lokální minimum s nejmenší hodnotou Epot. Chemický význam: Nejstabilnější uspořádání atomů a elektronů daného systému => Má nejvyšší pravděpodobnost výskytu v reálném chemickém prostředí.

Globální minimum v PES - vyhledávání • Metody prohledávání PES: – Systematické prohledávání (grid search) – Molekulová dynamika – Stochastické a Monte Carlo metody – Genetické algoritmy – Difuzní metody

Globální minimum v PES - vyhledávání II • Systematické prohledávání (grid search): Proloží hyperplochou mřížku a v jejích vrcholech vypočítá Epot. Tak zmapuje polohy lokálních minim a mezi nimi pak najde globální minimum. • Molekulová dynamika Viz předposlední přednáška : -).

Globální minimum v PES - vyhledávání III • Stochastické a Monte Carlo metody: Začínají v nějaké vstupní geometrii (nejčastěji v lokálním minimu. Nové konfigurace generují náhodným posunem jednoho nebo více atomů (random kick). • Genetické algoritmy: Základní myšlenkou je, že existují „populace“ objektů, z nichž každý má svou „množinu genů“. „Rodičovské“ objekty mohou tvořit „potomky“ kombinací svých genů (přičemž může docházet i k mutacím). Nejplodnější jedinci z populace jsou vybíráni a přenášeni do další generace. Tito jedinci jsou také „nejplodnější“.

Globální minimum v PES - vyhledávání III • Difuzní metody: Potenciálová funkce je postupně měněna tak, že ubývají lokální minima, až zaniknou všechna s vyjímkou globálního. Jsou prováděny například změny: – příspěvky ve směru kolmém k hyperploše => pro minima vzrůstá energie a pro maxima a sedlové body energie klesá

Literatura k MM • Leach A. R. : Molecular modelling. Longman (1996) • Jensen F. : Computational chemistry. Wiley (1999) • Grant G. H. , Richards W. G. : Computational chemistry. Oxford university press (1995) • Klikorka J. , Hájek B. , Votinský J. : Obecná a anorganická chemie. SNTL (1989)