Potaov chemie 9 pednka vod 1 pednka Molekula








































- Slides: 50

Počítačová chemie (9. přednáška) • Úvod (1. přednáška) • Molekula – Struktura molekuly (2. , 3. a 4. přednáška) – Geometrie molekuly (5. přednáška) – Vhled do praxe (6. přednáška) • Molekulové modelování – Molekulová mechanika (7. a 8. přednáška) – Kvantová mechanika (9. a 10. přednáška) – Molekulová dynamika (11. přednáška) – Vhled do praxe (12. přednáška)

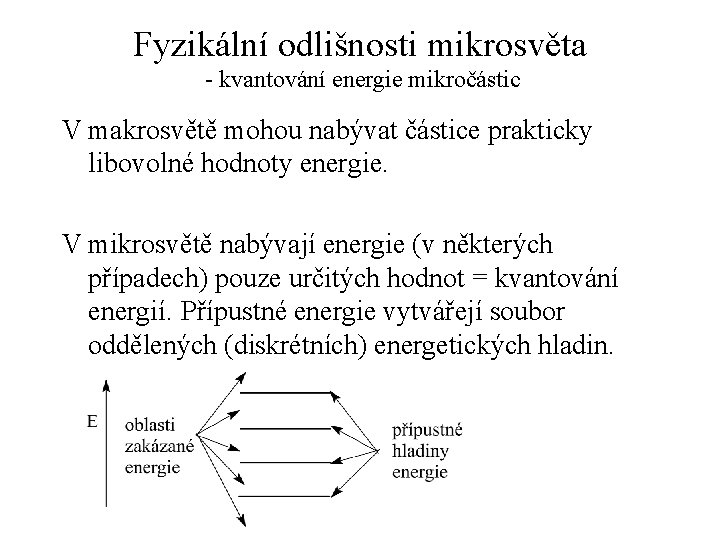
Fyzikální odlišnosti mikrosvěta - kvantování energie mikročástic V makrosvětě mohou nabývat částice prakticky libovolné hodnoty energie. V mikrosvětě nabývají energie (v některých případech) pouze určitých hodnot = kvantování energií. Přípustné energie vytvářejí soubor oddělených (diskrétních) energetických hladin.

Fyzikální odlišnosti mikrosvěta - kvantování energie mikročástic II Přechod částic z 1 hladiny na druhou je možný a je spojen s přijetím nebo odevzdáním množství energie, které odpovídá energetické vzdálenosti hladin. Částice nejdříve obsazují hladiny s nižší energií.

Fyzikální odlišnosti mikrosvěta - kvantování energie mikročástic III Kvantování bylo objeveno M. Planckem při studiu vlastností záření absolutně černého tělesa. Planck studoval závislost vlnové délky elektromagnetického záření tohoto tělesa na teplotě daného tělesa. Zjistil, že těleso vyzařuje jen záření určitých vlnových délek. Pro energii tohoto záření odvodil vztah: E = h. n, kde n je frekvence záření a h je Planckova konstanta (h = 6, 626 J. s*) * J. s = kg. m 2. s-1

Fyzikální odlišnosti mikrosvěta - dualistický charakter mikročástic Dualistický (korpuskulárně-vlnový) charakter mikročástic: – Korpuskulární charakter: • možnost přesné lokalizace v prostoru • existence definované trajektorie při pohybu • ostré vymezení povrchu – Vlnový charakter: • Vlnění se řídí se principem časově nejkratší dráhy: Směr šíření vln v prostoru je dán podmínkou, že podíl jejich dráhy a rychlosti musí být minimální – Dualistický charakter: Mikročástice se v některých experimentech chovají jako částice a v jiných jako vlnění.

Fyzikální odlišnosti mikrosvěta - dualistický charakter mikročástic II Příklad experimentu, potvrzujícího vlnový charakter elektronů: Proud elektronů nebo i molekul interferuje na krystalech. Příklad experimentu, potvrzujícího korpuskulární charakter elektromagnetických vln: Tok elektromagnetických vln při dopadu na tuhou podložku předává této podložce měřitelnou hybnost (pohyb nebo fotoelektrický jev).

Fyzikální odlišnosti mikrosvěta - Heisenbergův princip neurčitosti Součin každé dvojice dynamicky proměnných veličin, který má rozměr Planckovy konstanty, nemůže byt stanoven s menší nepřesností než je hodnota Planckovy konstanty. Příklad 1: hybnost ve směru osy x (px) a souřadnice na ose x (x): Dpx. Dx ³ h Příklad 2: energie (E) a čas (t): DE. Dt ³ h

Principy mechaniky mikrosvěta - úvod => Pro popis mikrosvěta nelze použít klasickou (Newtonovskou) mechaniku => Bylo nutno vytvořit novou mechaniku, vhodnou pro popis mikrosvěta: KVANTOVOU MECHANIKU (QM)

Principy mechaniky mikrosvěta - makrosvět a mikrosvět Makrosvět: Stav soustavy hmotných bodů = soubor informací o výsledcích všech nezávislých měření, provedených na soustavě (v uvažovaném časovém okamžiku). Pro určení stavu soustavy hmotných bodů je nutno znát: souřadnice a vektory hybnosti všech těchto bodů

Principy mechaniky mikrosvěta - makrosvět a mikrosvět II Mikrosvět: V mikrosvětě není možno provést současně měření určitých veličin (viz. Heisenbergův princip). => Stav soustavy mikročástic = soubor hodnot všech nezávislých veličin (v uvažovaném časovém okamžiku). V mikrosvětě nelze určit přesnou polohu mikročástic (pouze pravděpodobnost jejich výskytu), ani okamžitou rychlost (tedy ani hybnost) částic. Pro určení stavu soustavy je nutno znát jiný typ informace než v makrosvětě: vlnovou funkci daného systému

Principy mechaniky mikrosvěta - definice Norma vektoru y (|| y ||): Posloupnost vektorů {yn} je Cauchyovou posloupností, jestliže pro každé e > 0 existuje n 0 tak, že: pro každé n, m > n 0. Posloupnost vektorů {yn} konverguje k y, jestliže:

Principy mechaniky mikrosvěta - definice II Skalání součin vektorů u = {u 1, u 2, . . . , un} a v = {v 1, v 2, . . . , vn} v N-rozměrném VP: u. v = u 1. v 1 + u 2. v 2 +. . . + un. vn Diracovo označení: vektor v |v> skalární součin u. v <u|v> vektor u ze skalárního součinu u. v: bra-vektor, <u| vektor v ze skalárního součinu u. v: ket-vektor, |v> Poznámka: Názvy vznikly rozdělením slova bracket (závorka).

Principy mechaniky mikrosvěta - definice III Vektorový prostor (VP): množina vektorů, uzavřená k operacím + a * Unitární VP: VP v němž je definován skalární součin Úplný VP: VP, v němž každá Cauchyova posloupnost konverguje Hilbertův prostor = úplný unitární vektorový prostor.

Vlnová funkce Každému fyzikálnímu systému lze přiřadit jistý Hilbertův prostor H. Libovolný stav systému je plně popsán určitým vektorem y tohoto prostoru. Vektor y je někdy nazýván stavovým vektorem nebo častěji vlnovou funkcí. Jak funguje y jako funkce (pro soustavu mikročástic, popsanou P prostorovými souřadnicemi): y: RP+1 ® R Definičním oborem funkce y jsou (P+1)-rozměrné vektory prostorových souřadnic a času, tedy vektory tvaru: (s 1, s 2, . . . , s. P, t). Tyto vektory lze také zapsat jako (s, t), kde s = {s 1, s 2, . . . , s. P}. Vektor y reprezentuje funkci y: y(s, t) = (s, t). y Poznámka: V Diracově označení je y ket-vektor.

Vlnová funkce II Vektor y Î H => proto pro funkci y platí: – y je jednoznačná funkce – y je spojitá funkce – y je kvadraticky integrabilní (= existuje òy 2 dt) Chemický význam y: y 2 určuje pravděpodobnost výskytu mikročástice na daných souřadnicích v daném čase.

Vlnová funkce III ? Jak určit vlnovou funkci ? Pomocí Schrodingerovy rovnice! - tato rovnice nebyla odvozena, ale postulována

Schrodingerova rovnice - definice Postulát: Vlnová funkce y(s, t) vyhovuje Schrodingerově rovnici: Kde: H Hamiltonův operátor Planckova konstanta h/2 p i Poznámka: Výše uvedená rovnice se nazývá úplná Schrodingerova časová rovnice.

Schrodingerova rovnice - definice II Předpokládáme-li, že Hamiltonián nezávisí na čase, můžeme v předchozí rovnici separovat proměnné: Vlnovou funkci rozdělíme na časovou a prostorovou část: y(s, t) = y(s). h(t) Po dosazení tohoto vztahu do předchozí rovnice dostaneme: A po matematické úpravě: Levá strana rovnice je závislá jen na t, pravá jen na s, proto se musí obě strany rovnat téže konstantě, kterou si označíme E.

Schrodingerova rovnice - definice III Dostáváme tedy dvě rovnice: kde C je libovolná konstanta a Druhá z rovnic se nazývá bezčasová Schrodingerova rovnice a zapisujeme ji nejčastěji ve tvaru: E je konstanta a má z chemického hlediska význam energie systému.

Schrodingerova rovnice - obecný příklad Hamiltonián pro systém, obsahující jednu částici (například elektron) o hmotnosti m, nacházející se v externím poli (např. v poli, tvořeném atomovým jádrem) s potenciální energií V(r) = V(x, y, z): kde D je Lapalaceův operátor: Schrodingerova rovnice má pak tvar:

Schrodingerova rovnice - řešení Schrodingerova rovnice je diferenciální rovnicí druhého řádu. Řešeními Schrodingerovy rovnice jsou dvojice: (y, E), které splňují tuto rovnici. y je v této rovnici vlastní funkcí hamiltoniánu a konstanta E je vlastní hodnotou hamiltoniánu.

Schrodingerova rovnice - řešení II Analytické řešení Schrodingerovy rovnice je možné jen pro dvojici částic. Proto jen u atomu vodíku (proton + elektron) a systémů podobného typu můžeme přesně vypočítat vlastní hodnoty energie E a určit vlastní vlnové funkce. Ale výsledky analytického řešení Schrodingerovy rovnice pro atom vodíku jsou použitelným prototypem pro vytvoření představy o uspořádání atomů všech dalších známých chemických prvků.

Schrodingerova rovnice - využití Pro účely chemie se má vlnová funkce následující využití: Určuje pravděpodobnost výskytu elektronu v atomu => vymezuje existenční oblast elektronu v atomu. Tato oblast nejpravděpodobnějšího výskytu se nazývá atomový orbital (AO). Vlnová funkce každého AO je funkcí 3 prostorových souřadnic. Počátek systému soužadnic je vždy umístěn do jádra.

Atomový orbital - úvod Pro určitý systém tedy řešením Schrodingerovy rovnice získáme soubor vlnových funkcí a ke každé z nich také příslušnou energii. Každá vlnová funkce přísluší jednomu AO Každá vlnová funkce obsahuje 3 celá čísla, která jsou pro ní charakteristická (tzv. kvantová čísla).

Atomové orbitaly - kvantová čísla Kvantová čísla: • Hlavní kvantové číslo (n): – charakterizuje energii AO – nabývá hodnot: n = 1, 2, 3, . . . • Vedlejší kvantové číslo (l): – určuje tvar AO – nabývá hodnot: l = 0, 1, 2, . . . , n-1 • Magnetické kvantové číslo (ml): – určuje orientaci AO k souřadnému systému – nabývá hodnot: ml = -l, -l+1, . . . , -1, 0, 1, . . . , l-1, l

Atomové orbitaly - kvantová čísla II Spin: K popisu pohybu elektronu v atomu nastačí vlnová funkce Yn, l, ml. Elektron má totiž ještě specifickou vlastnost, která nemá analogii v klasické mechanice: vnitřní moment rotace neboli spin Hodnotu spinu vyjadřuje spinové kvantové číslo ms, které nabývá hodnot: 1/2 a -1/2 Pro popis pohybu elektronu v atomu je tedy nutno znát: Y a ms

Atomové orbitaly - kvantová čísla III Spin lze popsat spinovou funkcí h proměnné z, kde z nabývá hodnot 1/2 a -1/2: h(z) = a 1 pro z = 1/2 h(z) = a 2 pro z = -1/2 Jestliže definujeme ortonormální jednoelektronové spinové funkce a a b následovně: a(z) = 1 pro z = 1/2 a(z) = 0 pro z = -1/2 b(z) = 0 pro z = 1/2 b(z) = 1 pro z = -1/2

Atomové orbitaly - kvantová čísla IV Pak můžeme h(z) zapsat: h(z) = a 1. a(z) + a 2. b(z) Jednoelektronovou spin-orbitalovou funkci (spinorbital) y(s, z) lze tedy vyjádřit následovně: y(s, z) = y(s). a nebo y(s, z) = y(s). b

Atomové orbitaly - oblasti elektronového obalu Vrstva: Oblast nejpravděpodobnějšího výskytu elektronu s určitým hlavním kvantovým číslem. Značí se: K (n = 1), L (n = 2), M (n = 3), N (n = 4), . . . Orbit: Oblast nejpravděpodobnějšího výskytu elektronu s určitým hlavním a vedlejším kvantovým číslem. Značí se: s (l = 0), p (l = 1), d (l = 2), f (l = 3), . . . Orbital: Oblast nejpravděpodobnějšího výskytu elektronu s určitými kvantovými čísly. Spin-orbital: Oblast nejpravděpodobnějšího výskytu elektronu s určitými kvantovými čísly a spinem.

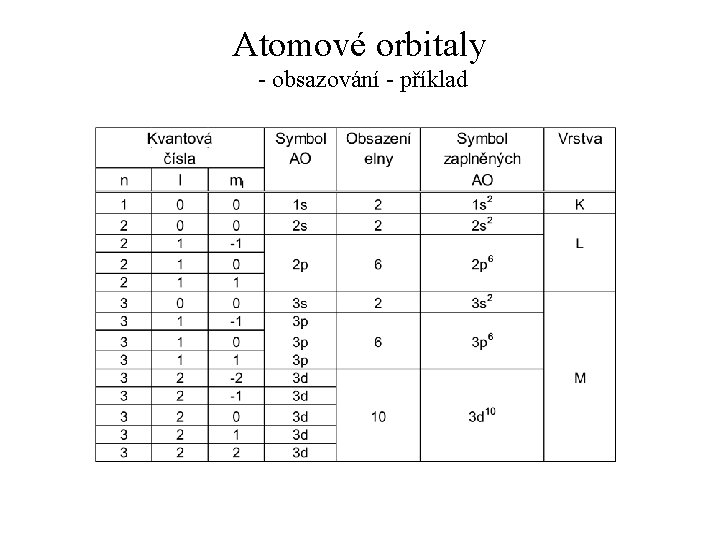
Atomové orbitaly - obsazování Pro obsazování AO elektrony platí Pauliho princip výlučnosti: Žádné dva elektrony nemohou v atomu existovat ve stejném kvantovém stavu (= mít stejná všechna kvantová čísla). Navíc platí výstavbový princip: Orbitaly s nižší energií nižší se zaplňují elektrony dříve než orbitaly s vyšší energií. => Lze snadno určit, kolik elektronů bude obsaženo v jednotlivých vrstvách, orbitech, orbitalech a spinorbitalech

Atomové orbitaly - obsazování - příklad

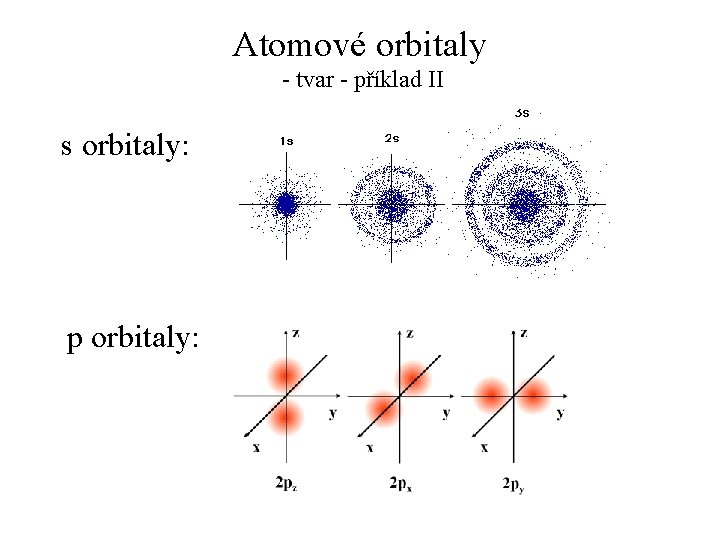
Atomové orbitaly - tvar - příklad II s orbitaly: p orbitaly:

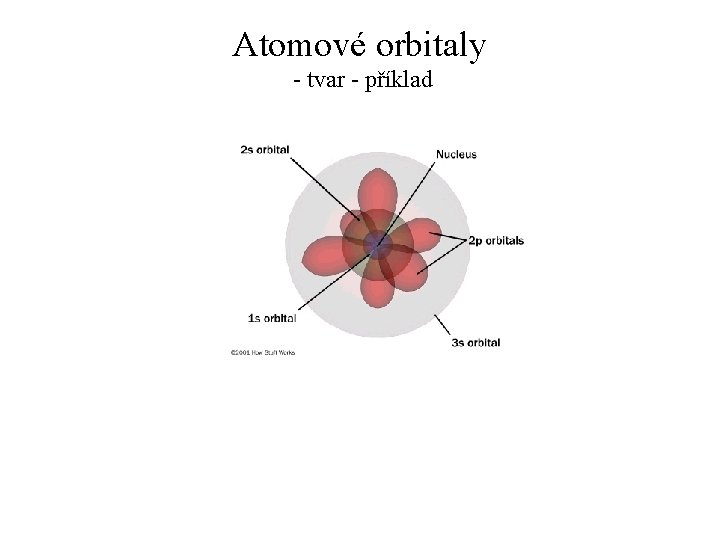
Atomové orbitaly - tvar - příklad

Atomové orbitaly - tvar - příklad III d orbitaly:

Schrodingerova rovnice - konkrétní příklad - atom H Pro Hamiltonián tohoto systému platí: kde: Z je počet protonů (Z = 1), r je vzdálenost elektronu od jádra e je náboj elektronu e 0 je permitivita vakua

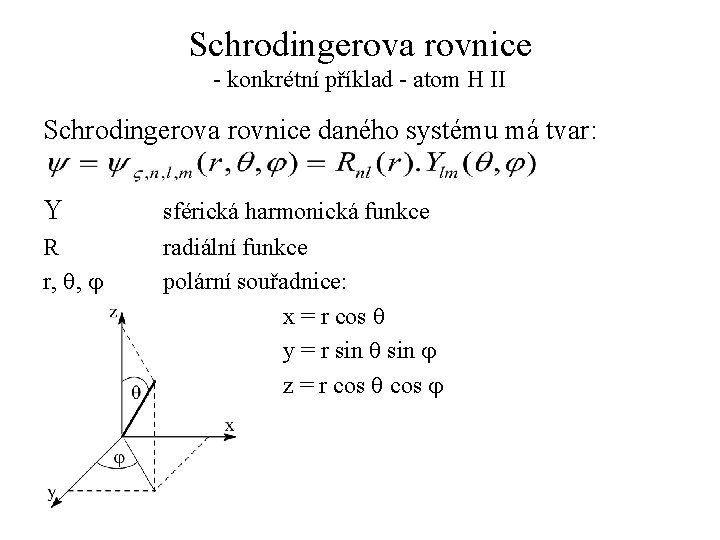
Schrodingerova rovnice - konkrétní příklad - atom H II Schrodingerova rovnice daného systému má tvar: Y R r, q, j sférická harmonická funkce radiální funkce polární souřadnice: x = r cos q y = r sin q sin j z = r cos q cos j

Schrodingerova rovnice - konkrétní příklad - atom H III Konkrétní příklady radiální funkce: n l radiální funkce 1 2 2 0 0 1 z orbitalový exponent: kde: a 0 Bohrův poloměr atomu H

Schrodingerova rovnice - konkrétní příklad - atom H IV Rozdělení sférické harmonické funkce: kde: asociované Legendrovy polynomy normalizační faktor

Molekulové orbitaly Základní představa: Molekula = polycentrický útvar, tvořený souborem atomových jader, v němž jsou na určitých orbitalech umístěny elektrony, patřící molekule. Tyto orbitaly se nazývají molekulové orbitaly (MO) a jsou analogií AO. Soubor MO lze získat řešením Schrodingerovy rovnice. Formulovat tuto rovnici pro molekulu není obtížné, ale řešení dané rovnice je prakticky nedostupné. I nejjednodušší systém (dvě atomová jádra a jeden elektron) lze řešit pouze přibližně a po zavadení některých zjednodušení. Tento způsob řešení se proto nepoužívá. Vhodnější je vyjádřit vlnové funkce MO pomocí vlnových funkcí AO.

y víceelektronových atomů a molekul Metoda MO-LCAO = Molecular orbital - linear combination of AO. = Model vazebné interakce dvou AO. = Metoda, která určuje vlnovou funkci MO pomocí lineární kombinace vlnových funkcí AO, jejichž průnikem MO vznikl. Princip metody: Prostorový průnik dvou AO, patřících dvěma atomům, které se k sobě přiblížily na vazebnou vzdálenost, se nazývá překryv. Velikost překryvu vyjadřujeme tzv. integrálem překryvu. Hodnoty S jsou mírou relativního průniku AO a pohybují se v intervalu od S = 0 (pro vzdálené atomy) do S = 1 (pro pomyslnou situaci, kdy je vzdálenost jader 0).

y víceelektronových atomů a molekul Metoda MO-LCAO II Dva pronikající se orbitaly AO¢ a AO² se při růstu hodnoty S mění na dvojici orbitalů MOb a MO*. MOb se nazývá vazebný orbital nebo také symetrický orbital a má menší energii než původní AO¢ a AO². Právě v tomto orbitalu se po vzniku vazby budou nacházet oba elektrony, účastnící se vazby => Vzniklý systém bude mít menší energii než původní systém. MO* se nazývá antivazebný orbital nebo také antisymetrický orbital a má vyšší energii než původní AO¢ a AO². Není obsazován elektrony a když k tomuto obsazení přece jenom dojde, tak působí proti vzniku vazby.

y víceelektronových atomů a molekul Metoda MO-LCAO III Pro vlnové funkce y(MOb) a y(MO*) molekulových orbitalů MOb a MO*, vzniklých průnikem atomových orbitalů AO¢ a AO², platí: y(MOb) = c¢. y(AO¢) + c¢¢. y(AO¢¢) y(MO*) = c¢. y(AO¢) - c¢¢. y(AO¢¢) c¢ a c¢¢ jsou váhové konstanty, které popisují, jakým podílem přispívají původní AO do MO Příklad - vznik MO molekuly H 2: 1 sb = 1 s + 1 s 1 s* = 1 s - 1 s

y víceelektronových atomů a molekul Metoda MO-LCAO IV Poloha energetických hladin E(MOb) a E(MO*) je v případě, že se pronikají tytéž AO dvou atomů téhož prvku, vyjádřena vztahy: Kde: a coulombický integrál, vyjadřuje energii obou pronikajících se AO v době, kdy byly izolované b rezonanční nebo také výměnný integrál, vyjadřuje interakční energii obou původních AO a je závislá na velikosti S.

y víceelektronových atomů a molekul Metoda MO-LCAO V Příklad: Molekula HF energie AO a MO.

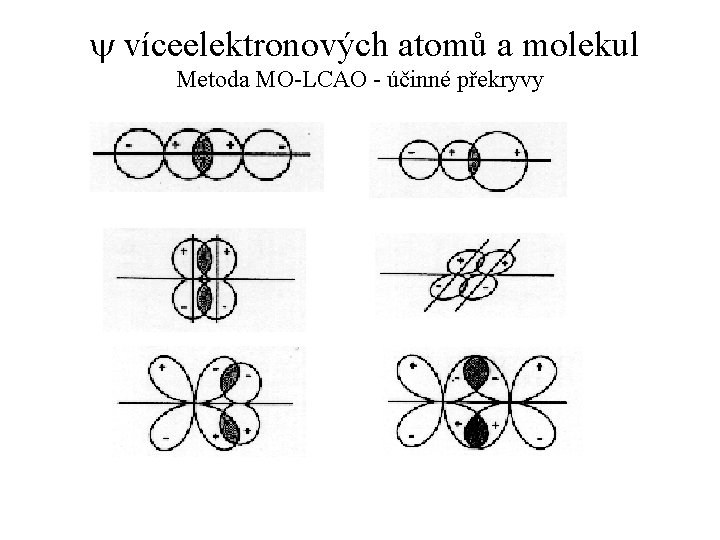
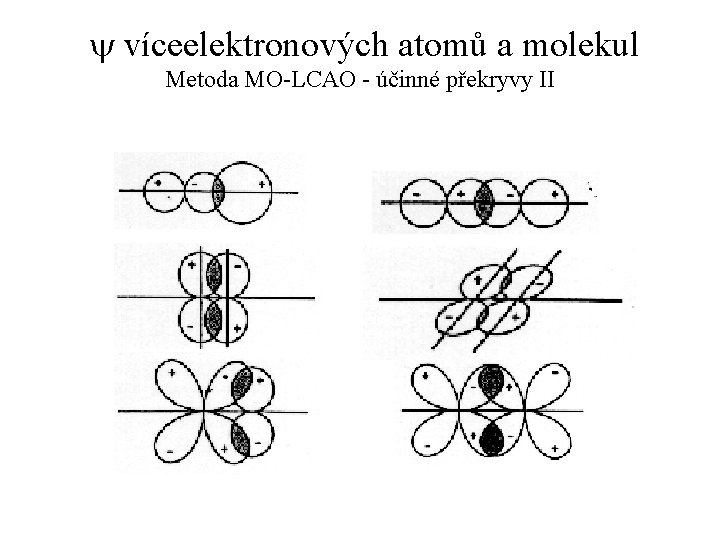
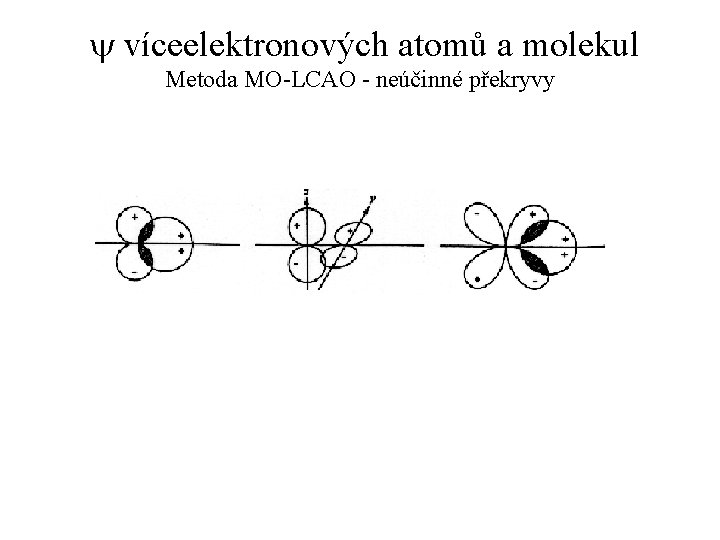
y víceelektronových atomů a molekul Metoda MO-LCAO VI Překryv dvojice AO je účinný (= skutečně vede k vytvoření energeticky diferencovaných orbitalů MOb a MO*) pouze tehdy, když nemají původní AO¢ a AO² příliš rozdílnou energii. Počet MO, které vzniknou překryvem, je vždy roven počtu AO, které se překryvu účastní. K účinnému překryvu dojde pouze tehdy, když mají AO¢ a AO² stejnou symetrii k ose chemické vazby (viz obrázek). Energetická diference mezi dvojicí vzniklých orbitalů MOb a MO* je tím větší, čím větší je integrál překryvu S původních AO¢ a AO².

y víceelektronových atomů a molekul Metoda MO-LCAO - účinné překryvy

y víceelektronových atomů a molekul Metoda MO-LCAO - účinné překryvy II

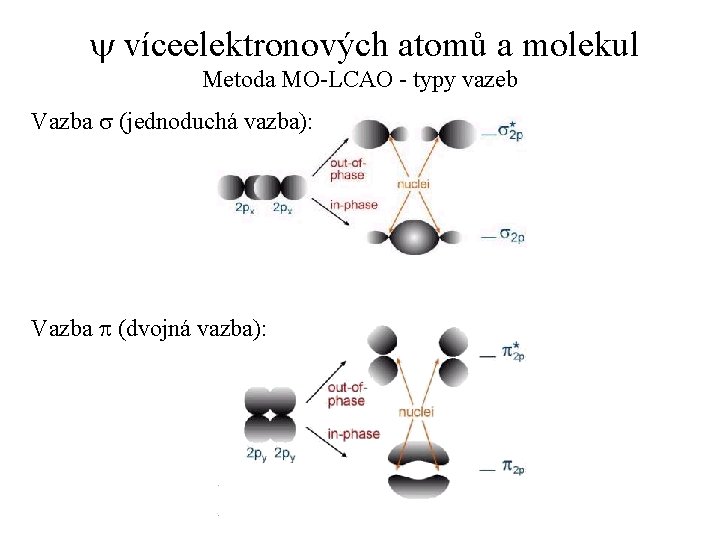
y víceelektronových atomů a molekul Metoda MO-LCAO - typy vazeb Vazba s (jednoduchá vazba): Vazba p (dvojná vazba):

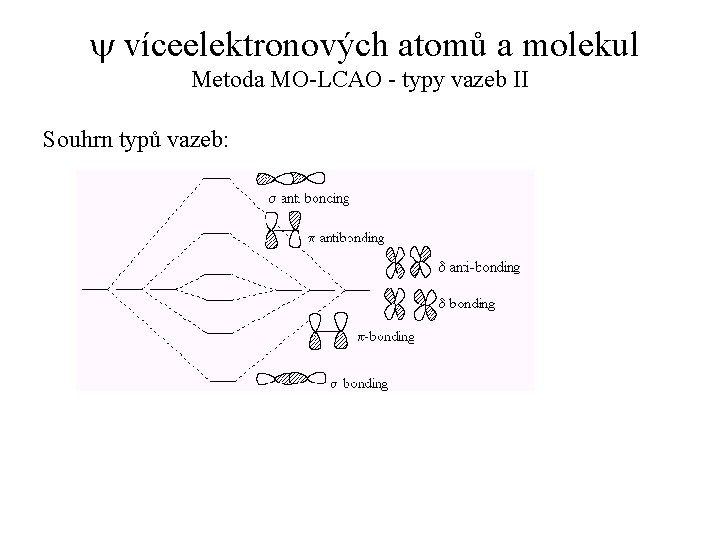
y víceelektronových atomů a molekul Metoda MO-LCAO - typy vazeb II Souhrn typů vazeb:

y víceelektronových atomů a molekul Metoda MO-LCAO - neúčinné překryvy
 Diagnostika potaov toshiba
Diagnostika potaov toshiba Diagnostika potaov hp
Diagnostika potaov hp Co je to marketing
Co je to marketing Vod marketing
Vod marketing Zakupljeni vod
Zakupljeni vod Vod
Vod Tulipan vod
Tulipan vod Trojan iptv
Trojan iptv Rw + vo c inverter transient response vod inverte...
Rw + vo c inverter transient response vod inverte... Ztv vod
Ztv vod Iptv vod italia
Iptv vod italia Nadzemni vod
Nadzemni vod Ztv vod
Ztv vod Znakovlje
Znakovlje Maketa dna molekule
Maketa dna molekule Raspodela molekula gasa po brzinama
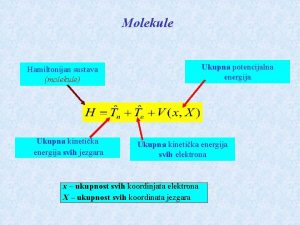
Raspodela molekula gasa po brzinama Molekula
Molekula Molekula
Molekula Kohezione sile
Kohezione sile Molekula
Molekula Mhc molekula
Mhc molekula Molekula vodíku
Molekula vodíku Polarizabilnost
Polarizabilnost Molekula
Molekula Molekulsko kineticka teorija gasova
Molekulsko kineticka teorija gasova Nitrace naftalenu
Nitrace naftalenu Szilícium
Szilícium 1 molekula vody
1 molekula vody Naturfasern übersicht
Naturfasern übersicht Areny chemie
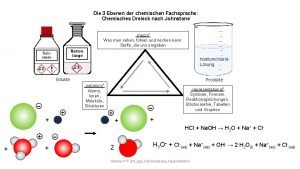
Areny chemie Johnstone dreieck
Johnstone dreieck Oxidy koncovky
Oxidy koncovky Chemie
Chemie Sucha chemie
Sucha chemie Fehlvorstellungen chemie
Fehlvorstellungen chemie Voda prezentace chemie
Voda prezentace chemie Atoomeconomie
Atoomeconomie Impuls chemie 4
Impuls chemie 4 Ppp chemie
Ppp chemie Steigerleren
Steigerleren Esterhydrolyse
Esterhydrolyse Substrat chemie
Substrat chemie Impuls chemie 4 lösungen pdf
Impuls chemie 4 lösungen pdf Impuls chemie
Impuls chemie Sbr6 chemie
Sbr6 chemie Chemie
Chemie Hhu mediathek
Hhu mediathek Lauterbur
Lauterbur Cyclopropaan
Cyclopropaan Burgerlijk ingenieur chemie
Burgerlijk ingenieur chemie Skelettschreibweise
Skelettschreibweise