Parallel Sorting Algorithms Oct 25 2012 copyright 2012

Parallel Sorting Algorithms Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

• The simple sorting algorithms (Bubble Sort, Insertion Sort, Selection Sort, …) are • Lower bound on comparison based algorithms (Merge Sort, Quicksort, Heap Sort, …) is • The best we can hope to do with parallelizing a comparison-based algorithm using n processors is Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

• Question: What can we expect if we use n 2 processors? • Answer: Typically, it is still: Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

• In place sorting – sorting the values within the same array • Not in-place (or out-of-place) sorting – sorting the values to a new array • Stable sorting algorithm – Identical values remain in the same order as the original after sorting Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Compare and Exchange • Most sorting algorithms (although not all) compare two values and possibly exchange them • Two numbers in the array are compared with each other: if (A[i] temp A[i] A[j] } Oct 25, 2012 > = = = A[j]) { A[i]; A[j]; temp; © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Message-passing Compare and Exchange (version 1) • In a distributed-memory system, we have to send message to exchange values • P 1 send value to P 2 compares the two values; keeps the larger and sends the smaller back to P 1 Processor 1 A[i] Processor 2 A[i] is sent A[i] A[j] Smaller Value Returned Oct 25, 2012 Larger Value Kept © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

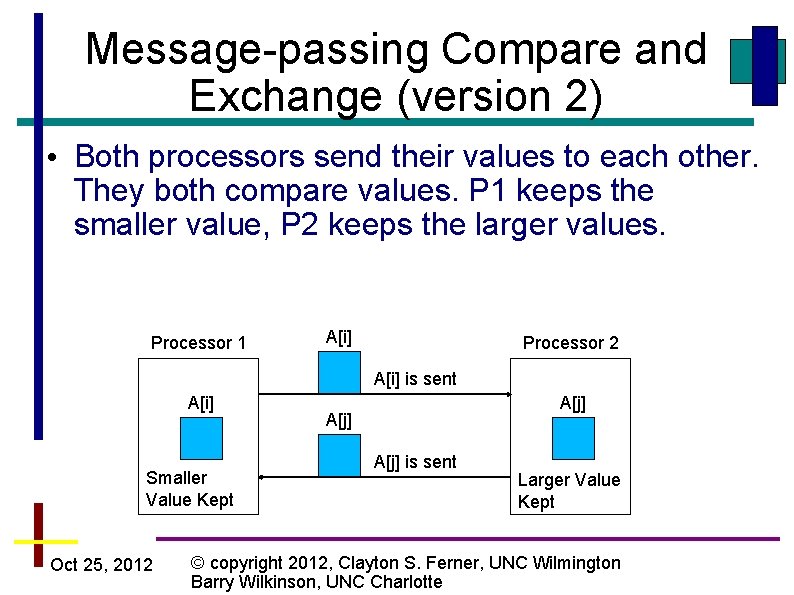
Message-passing Compare and Exchange (version 2) • Both processors send their values to each other. They both compare values. P 1 keeps the smaller value, P 2 keeps the larger values. Processor 1 A[i] Processor 2 A[i] is sent A[i] Smaller Value Kept Oct 25, 2012 A[j] is sent Larger Value Kept © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

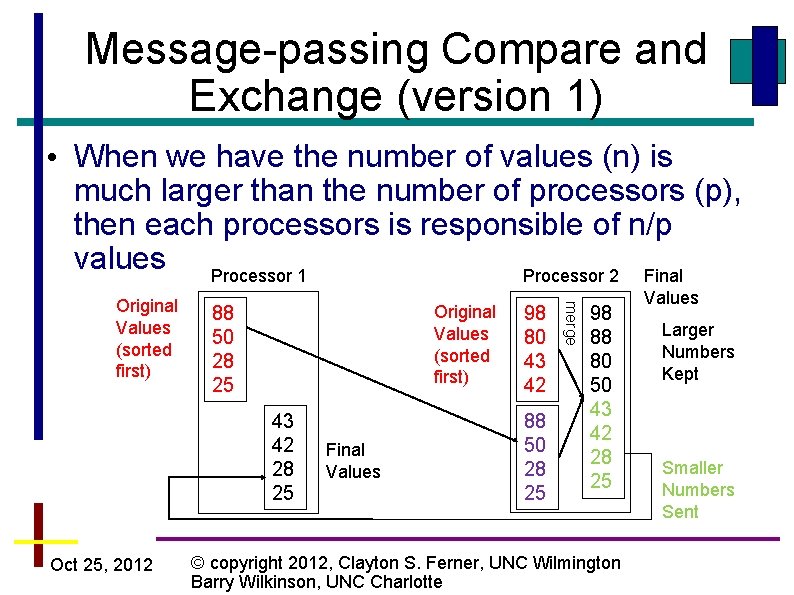
Message-passing Compare and Exchange (version 1) • When we have the number of values (n) is much larger than the number of processors (p), then each processors is responsible of n/p values Processor 1 Processor 2 Final Original Values (sorted first) 88 50 28 25 43 42 28 25 Oct 25, 2012 Final Values 98 80 43 42 88 50 28 25 merge Original Values (sorted first) 98 88 80 50 43 42 28 25 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte Values Larger Numbers Kept Smaller Numbers Sent

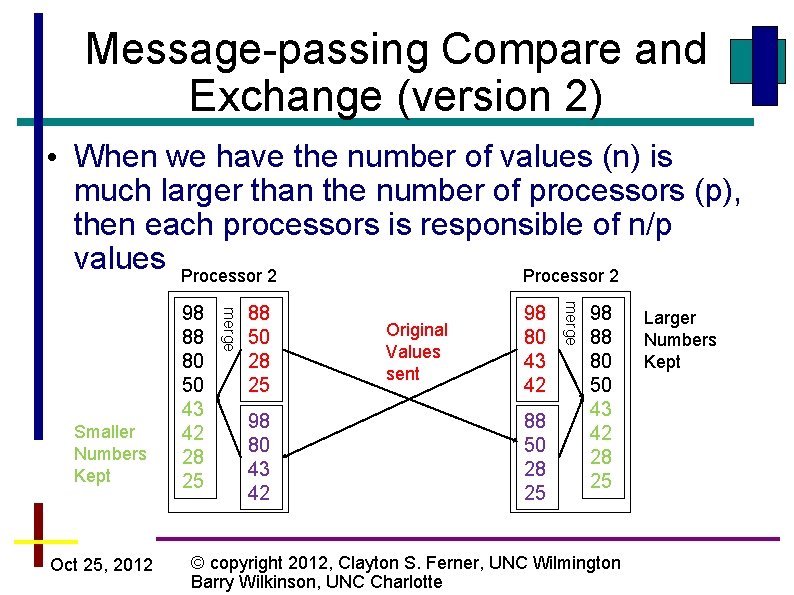
Message-passing Compare and Exchange (version 2) • When we have the number of values (n) is much larger than the number of processors (p), then each processors is responsible of n/p values Processor 2 88 50 28 25 98 80 43 42 Original Values sent 98 80 43 42 88 50 28 25 merge Oct 25, 2012 merge Smaller Numbers Kept 98 88 80 50 43 42 28 25 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte Larger Numbers Kept

Parallelizing Common Sorting Algorithms Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

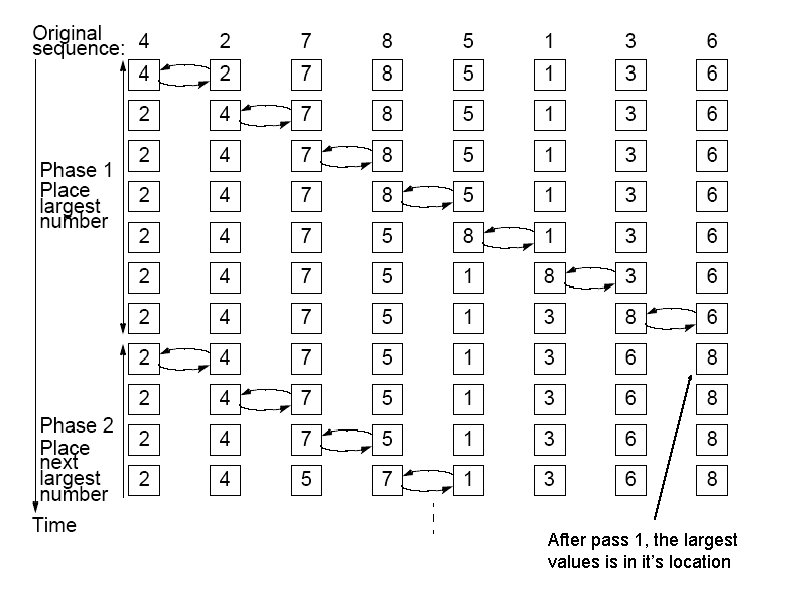
Bubble Sort • N passes are made comparing/exchanging adjacent values • Larger values settle to the bottom (Sediment Sort? ) • After pass m, the m largest values are in the m last locations in the array. Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

After pass 1, the largest values is in it’s location

Complexity of Bubble Sort • The number of comparison/exchanges with Bubble Sort is: • Very slow but easy to parallelize • We can use a pipeline-sort of technique Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Parallel Bubble Sort P 0 P 1 P 2 P 3 P 4 P 5 P 6 P 7 Phase 1 Time Phase 2 Phase 3 Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Even-Odd Transposition Sort • Uses alternating even and odd phases – Even phase • even processors exchange with next higher ranked processor • odd processors exchange with the next lower ranked processor – Odd phase • even processors exchange with next lower ranked processor • odd processors exchange with the next higher ranked processor Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Even-Odd Sort Time P 0 P 1 P 2 P 3 P 4 P 5 P 6 P 7 4 2 7 8 5 1 3 6 2 4 7 8 1 5 3 6 2 4 7 1 8 3 5 6 2 4 1 7 3 8 5 6 2 1 4 3 7 5 8 6 1 2 3 4 5 7 6 8 1 2 3 4 5 6 7 8 Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

• What is the time complexity of Parallel Bubble Sort with n processors? • Answer: 2 n=O(n) • What is the time complexity of Even-Odd Sort with n processors? • Answer: O(n) Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Divide and Conquer Pattern • Characterized by dividing problem into subproblems of same form as larger problem. • Further divisions into still smaller sub-problems, usually done by recursion. Creates a tree. • Recursive divide and conquer amenable to parallelization because separate processes can be used for divided parts. Also usually data becomes naturally localized. Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

• Sorting - Several sorting algorithms can often be partitioned or constructed in a recursive divide and conquer fashion, e. g. Mergesort, Quicksort, • Searching algorithms dividing search space recursively Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

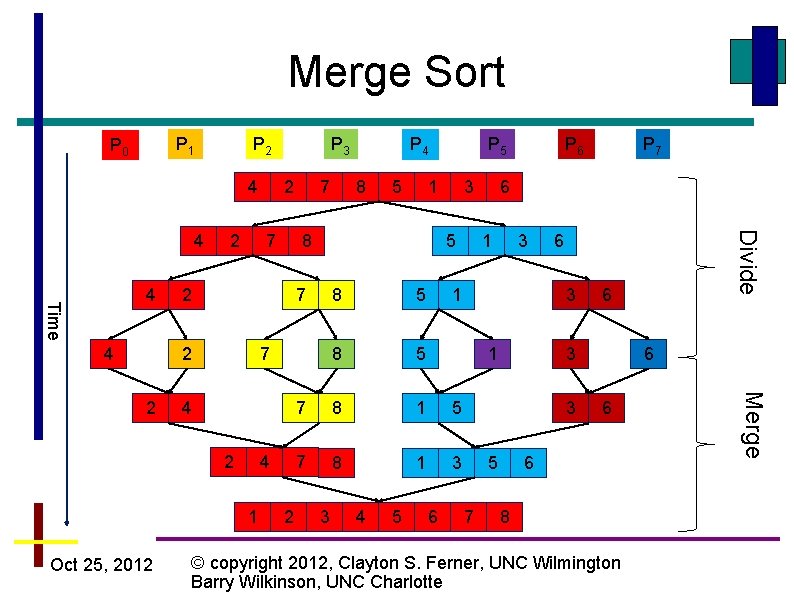
Merge Sort • Merge Sort is a “Divide and Conquer” algorithm • The array is divided into smaller and smaller parts • Then the small parts are merged into a new sorted sub array Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Merge Sort P 1 P 0 P 2 4 Time 4 4 2 7 5 1 5 8 5 7 8 1 5 4 7 8 1 3 2 3 4 5 P 6 6 1 3 1 6 6 3 3 5 7 P 7 6 6 6 8 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte Merge 4 3 8 7 1 8 P 5 5 7 2 Oct 25, 2012 7 8 2 2 P 4 Divide 4 P 3

Complexity of Parallel Merge Sort • Complexity of the sequential merge sort: • Complexity of parallel merge sort with n processors – There are 2 logn steps, but each merge step takes longer and longer – Turns out to be: Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

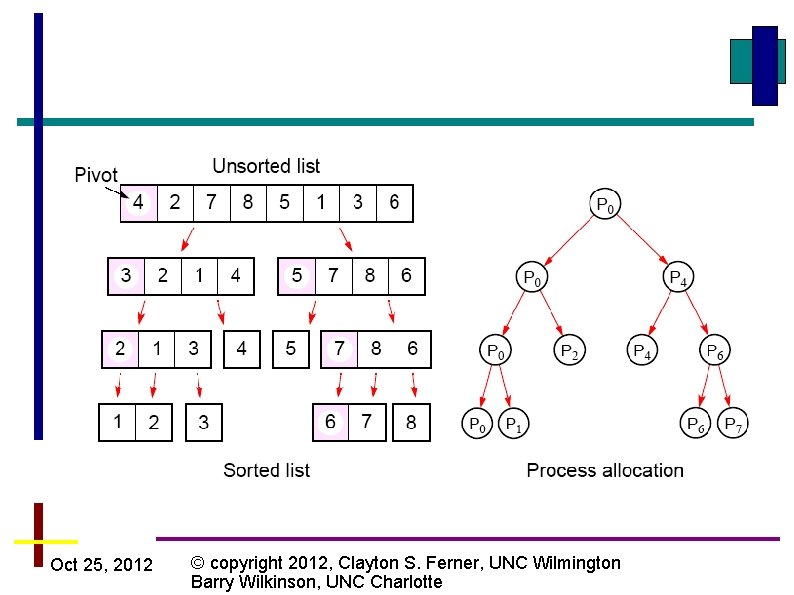
Quicksort • Pick a pivot • The move all the values less than the pivot to the left side of the array • And all the values greater than the pivot to the right side • Then recursively sort the two sides Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Quicksort • Works well when the pivot is approximately in the middle • If the pivot is chosen poorly, quicksort resorts to Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

• Neither Merge Sort nor Quicksort parallelize efficiently • Still • Any tree structure (reduction, merge, quicksort) cannot be parallelized by n processors efficiently Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

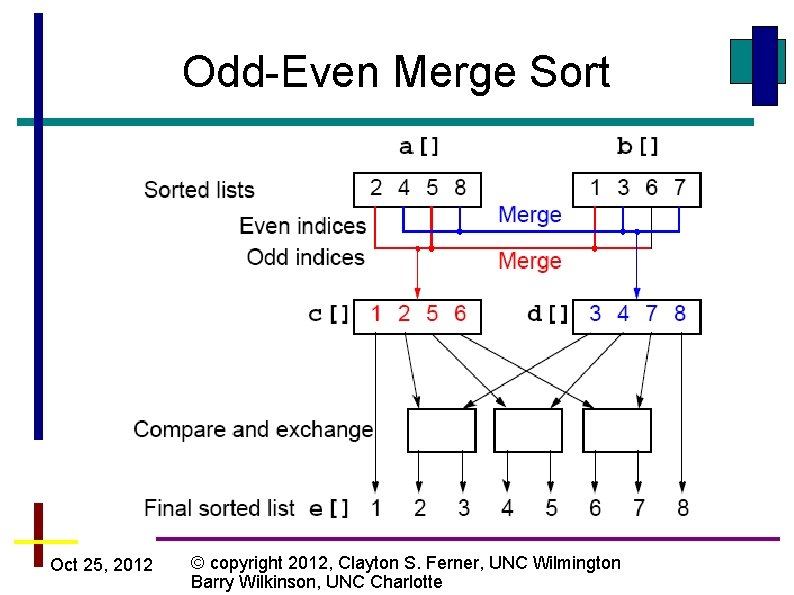
Batcher’s Parallel Sorting Algorithms • Odd-even Merge Sort (not the same as evenodd transposition sort) • Bitonic Merge Sort • Complexity with n processors: Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Odd-Even Merge Sort Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

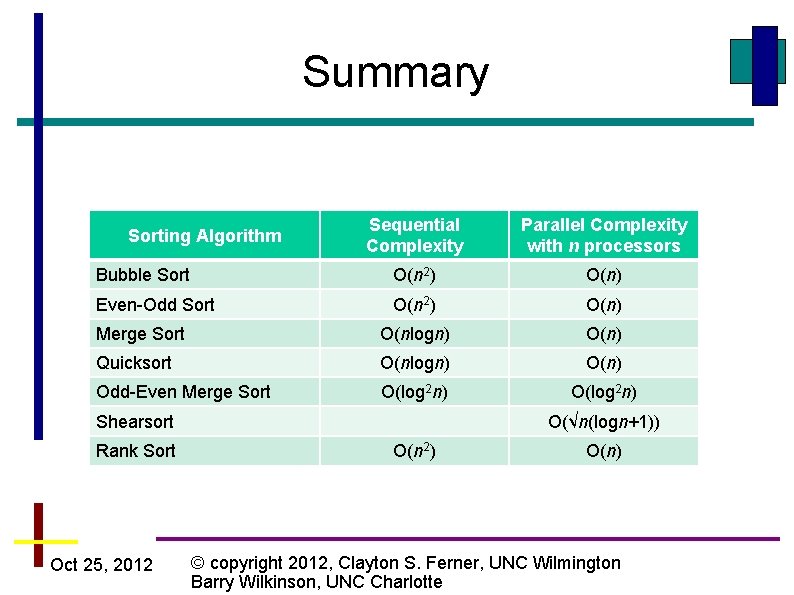
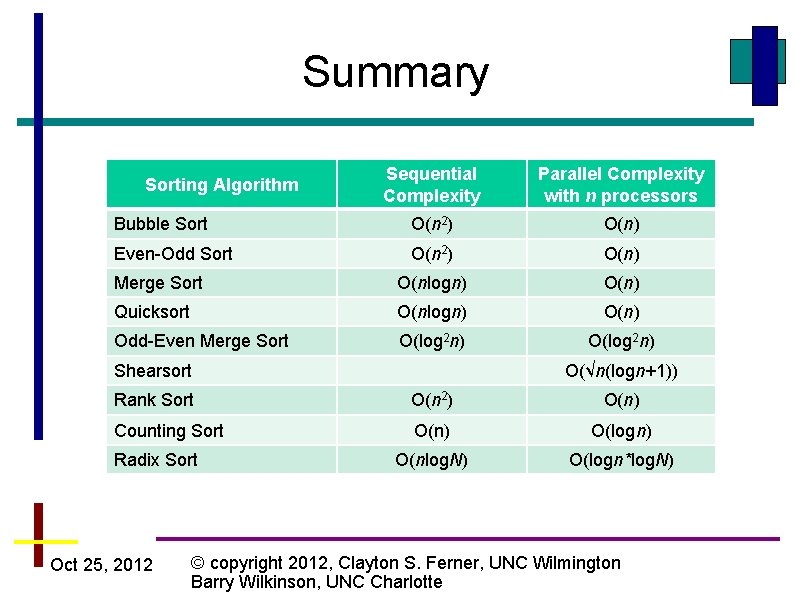
Summary (using n processors to sort n numbers) • Parallel Bubble sort and Odd-even transposition sort O(n) • Parallel mergesort - O(n) but unbalanced processor load and communication (because of tree) • Parallel quicksort - O(n) but unbalanced processor load and communication (because of tree) and can degenerate to O(n 2) • Odd-even Mergesort - O(log 2 n) Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

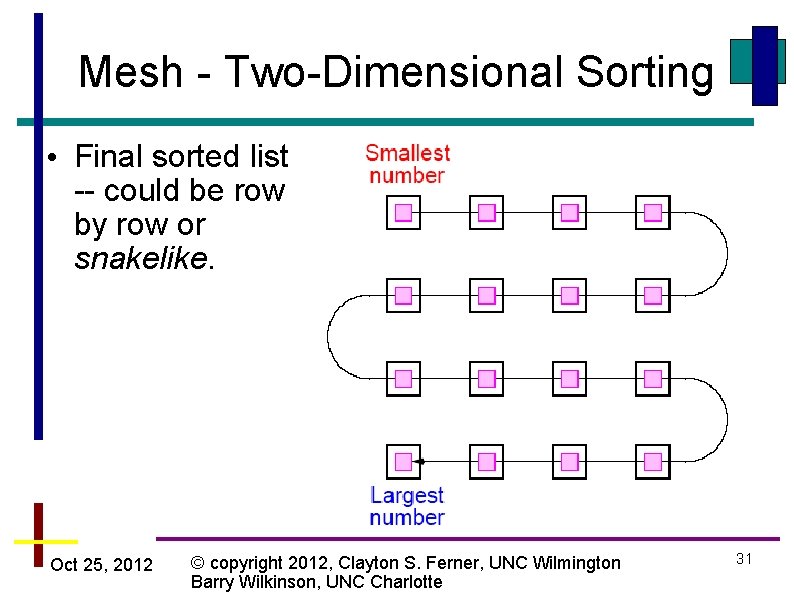
Sorting on Specific Networks • Two network structures have received specific attention: – Mesh – Hypercube • because parallel computers have been built with these networks. • Of less interest nowadays because underlying architecture often hidden from user. • There are MPI features for mapping algorithms onto meshes. • Can always use a mesh or hypercube algorithm even if the underlying architecture is not the same. Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 30

Mesh - Two-Dimensional Sorting • Final sorted list -- could be row by row or snakelike. Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 31

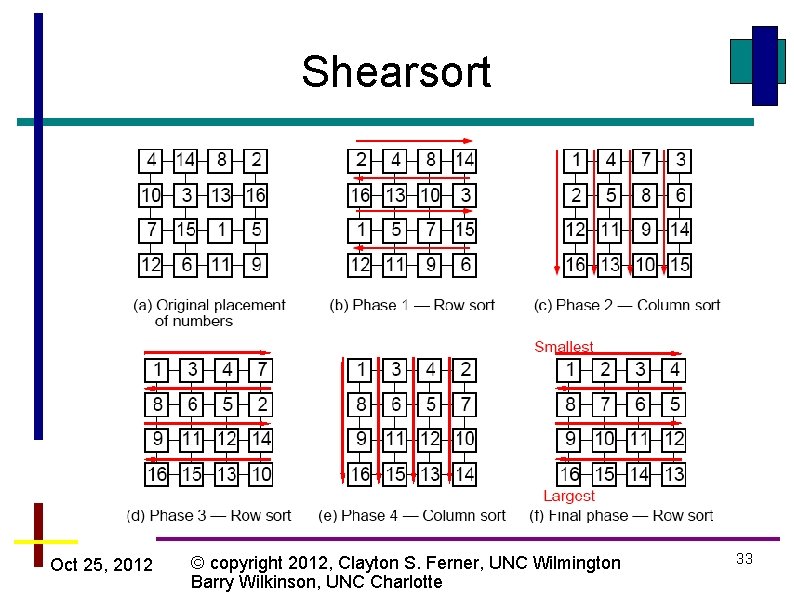
Shearsort • Alternate row and column sorted until list fully sorted • Result is a snake-like sorting • On a mesh, this requires steps Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 32

Shearsort Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte 33

Other Sorts (Coming Up Next) • Rank Sort • Counting Sort • Radix Sort Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Rank Sort • The idea of rank sort is to count the number of values less than a[i] • That count is the “rank” of that value • The rank is where in the sorted array that value will be placed • So we can put in into that spot b[rank] = a[i]. Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Rank Sort (Sequential Code) for (i = 0; i < n; i++) { x = 0; for (j = 0; j < n; j++) if (a[i] > a[j]) x++; b[x] = a[i]; } // for each number // count number less than it // copy number into correct place • Doesn’t handle duplicate values (How can this be fixed? ) • The complexity is O(n 2) • However, this is easy to parallelize Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Rank Sort (Parallel Code) forall (i = 0; i < n; i++) { // each processor allocated different value x = 0; for (j = 0; j < n; j++) // count number less than it if (a[i] > a[j]) x++; b[x] = a[i]; // copy number into correct place } • Uses n processors and complexity is O(n) • Very easy to implement in Open. MP • As good as many of the parallel sorts (except bitonic and shear sort) Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

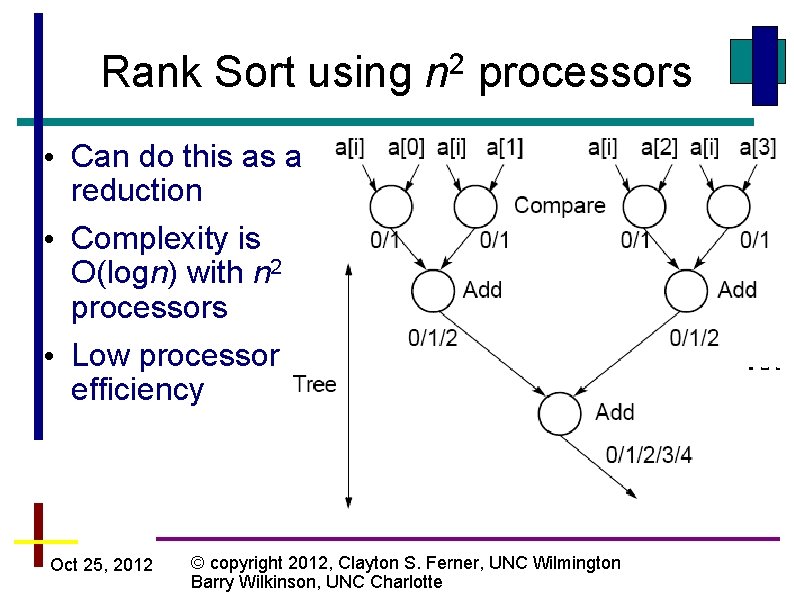
Rank Sort using n 2 processors • Instead of one processors comparing a[i] with other values, we use n-1 processors • Incrementing counter is a critical section; must be sequential, so this is still O(n) Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Rank Sort using n 2 processors • Can do this as a reduction • Complexity is O(logn) with n 2 processors • Low processor efficiency Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Summary Sequential Complexity Parallel Complexity with n processors Bubble Sort O(n 2) O(n) Even-Odd Sort O(n 2) O(n) Merge Sort O(nlogn) O(n) Quicksort O(nlogn) O(n) Odd-Even Merge Sort O(log 2 n) Sorting Algorithm Shearsort Rank Sort Oct 25, 2012 O(√n(logn+1)) O(n 2) O(n) © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Counting Sort • The best sequential sorting algorithms are O(nlogn). • We can do better if we can make assumption about the data • If the values are all integers within a relatively small range of values, we can do Counting Sort in O(n) instead of O(n 2) or O(nlogn). Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Counting Sort • Counting Sort is a stable sort (identical values remain in same relative position as in orginal array) • However, it is not an “in-place” sort • Further more, we need extra space • Suppose original values in the array a[ ] • Sorted array will be b[ ] • Create an array c[ ] of size m where values of a[ ] are in the range 1. . m. Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Counting Sort – Step 1 • c[ ] is the histogram of values in the array. In other words, it is the sum of equal values • Complexity is O(m + n) for (i = 1; i <= m; i++) c[i] = 0; for (i = 1; i <= n; i++) c[ a[i] ]++; Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Counting Sort – Step 2 • We can find the rank of each value by doing a prefix sum on c[ ] c[0] c[1] c[2] c[3] c[4] c 0+ c 1+ c 2+ c 3 c 0+ c 1+ c 2+ c 3+ c 4 … for (i = 2; i <= m; i++) c[i] = c[i] + c[i-1]; • Complexity is O(m) Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Counting Sort – Step 3 • We can now use the prefix sum to place the values where they should go: for (i = n; i >= 1; i--) { b[ c[ a[i] ] ] = a[i] c[ a[i] ]--; // ensures stable sorting } • Sequential complexity for all 3 steps is O(m + n) • If m is linear with n, then complexity is O(n) Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Counting Sort 1 2 3 4 5 6 7 8 a[] 5 2 3 7 5 6 4 1 Step 1. Histogram c[] 1 1 2 1 1 Step 2. Prefix sum c[] 1 2 3 4 6 7 8 Step 3. Sort b[] 1 2 3 4 5 5 6 Original sequence Step 3 moves backwards thro a[] 7 Final sorted sequence Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte Move 5 to position 6. Then decrement c[5]

Parallel Counting Sort (using n processors) • Step 1 – Creating the Histogram: O(logn). We use the same tree as with rank sort. Updating c[a[i]]++ is a critical section when there are duplicate values in a[ ]. • Step 2 – Parallel version of prefix sum using n processors is O(logn) • Step 3 – Placing number in place: O(logn) again because of possible duplicate values (c[a[i]]– is a critical section) • All 3 steps: O(logn) Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

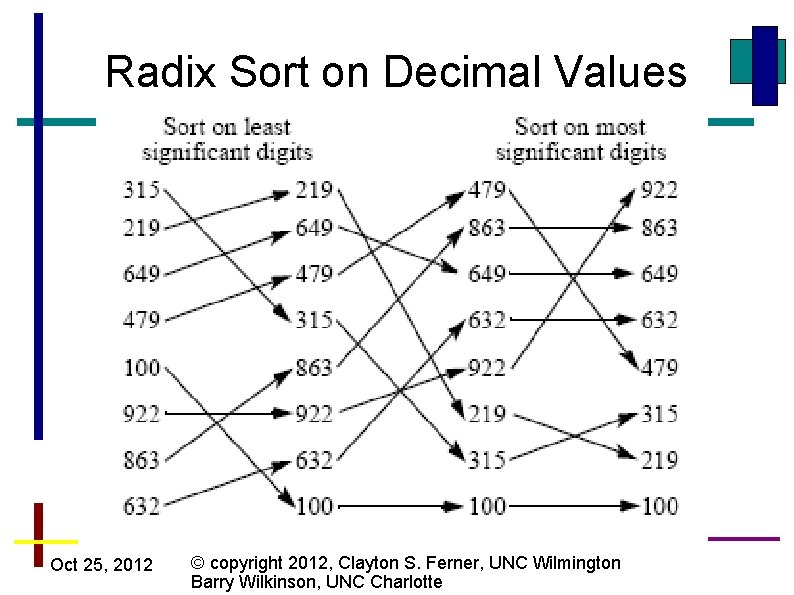
Radix Sort • Assumption: Values are either unsigned decimal or unsigned binary • Sort values based on least significant digit • Then sort on next least significant digit • Continue until the most significant digit is used to sort. • This works if we use a stable sorting algorithm • Since each digit will be in the range 0 -9 or 0 -1, then we can use Counting Sort for each digit Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Radix Sort on Decimal Values Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Radix Sort on Binary Values Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Radix Sort • When sorting binary values, we can improve the counting sort • To sort a column of bits, the prefix sum gives us the number of 1’s • We can use that to place the ones (decremented each time to deal with the duplicates) • The prefix sum of the inverse of the bits (called the diminished prefix sum) gives us the number of 0’s and can be used to place the zeros. • The complexity of sorting this column is O(logn), same as using counting sort on the column Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Radix Sort • The complexity of Radix Sort is the complexity of sorting each digit times the number of digits • If the range of values is 1. . N, then the number of digits is log 2 N for binary numbers and log 10 N for decimal. • O(logn*log. N) where n is the number of values and N is the range of values Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Summary Sequential Complexity Parallel Complexity with n processors Bubble Sort O(n 2) O(n) Even-Odd Sort O(n 2) O(n) Merge Sort O(nlogn) O(n) Quicksort O(nlogn) O(n) Odd-Even Merge Sort O(log 2 n) Sorting Algorithm Shearsort O(√n(logn+1)) Rank Sort O(n 2) O(n) Counting Sort O(n) O(logn) O(nlog. N) O(logn*log. N) Radix Sort Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte

Questions Oct 25, 2012 © copyright 2012, Clayton S. Ferner, UNC Wilmington Barry Wilkinson, UNC Charlotte