C Programming Week 10 Sorting Algorithms 1 Sorting

C Programming Week 10 Sorting Algorithms 1

Sorting n In many queries we handle a list of values and want a specific value. n n We can go through all the list until we find the requested value. But better… We can sort the list and then find it more easily (e. g. , by binary search)

Sorting • In class we saw several examples for sorting: – Bubble Sort – Merge Sort • Today we will continue with examples… • In these examples, each time we compare between two elements, resulting in a sorted list.

Quick Sort • Divide and conquer – Divide the list into two sublists such that all elements from one list are greater than all elements from other list. – Sort each of these sublists recursively…

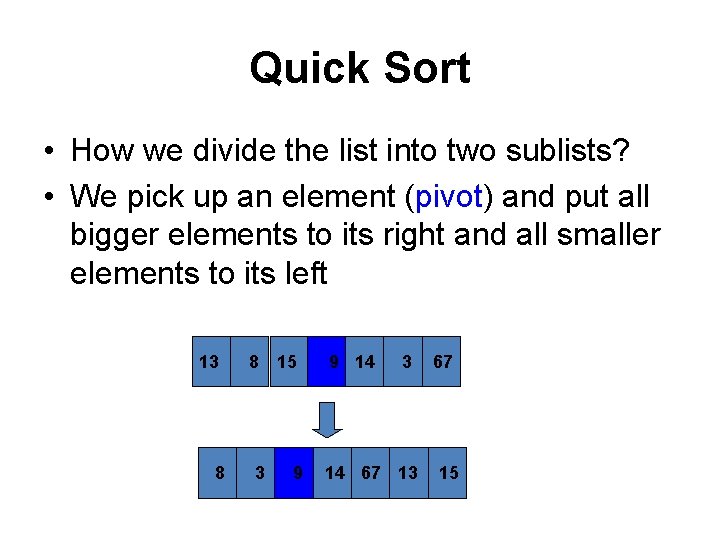
Quick Sort • How we divide the list into two sublists? • We pick up an element (pivot) and put all bigger elements to its right and all smaller elements to its left 13 8 8 3 15 9 9 14 3 14 67 13 67 15

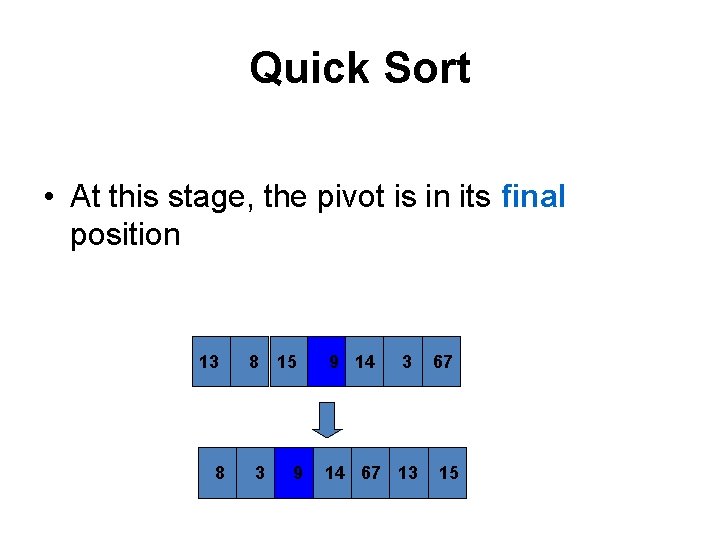
Quick Sort • At this stage, the pivot is in its final position 13 8 8 3 15 9 9 14 3 14 67 13 67 15

How do we choose the pivot? • Ideally, we should take the median value • However, it would take time to find what is the median, so we can take the: – First – Middle – Last – Any random element • In practice, each such choice is relatively efficient.

Some visualization… • http: //www. youtube. com/watch? v=vx. ENKlcs 2 Tw • http: //www. youtube. com/watch? v=y_G 9 Bk. Am 6 B 8

How do we implement this? • First, we look on the ‘backbone’ of the algorithm: – Partitioning the list according to a pivot into two sublists. – After this stage, the pivot value is in its final position. – Recursively repeat this procedure to each of the two sublists.

Quick Sort (backbone) void quick. Sort (int list[], int start_index, int end_index) // This function implements the Quick Sort algorithm { int pivot_index; if (start_index<end_index) // more than one element in list { // We now partition the list into two sublists: pivot_index=partition(list, start_index, end_index); // Where is the termination of the recursive function? Performing Quick Sort on both sublists: quick. Sort(list, start_index, pivot_index-1); quick. Sort(list, pivot_index+1, end_index); } } 10

Partition int partition (int list[], int start_index, int end_index) { int i, j; int pivot_index=choose. Pivot(start_index, end_index); int pivot_value=list[pivot_index]; swap(&list[start_index], &list[pivot_index]); i=start_index+1; j=end_index; while (i<=j) { while ((i<=end_index) &&(list[i]<=pivot_value)) i++; while ((j>=start_index) && (list[j]>pivot_value)) j--; if (i<j) swap(&list[i], &list[j]); } swap(&list[start_index], &list[j]); pivot_index=j; return pivot_index; } 11

main int main() { int array[SIZE]={0}; int i; printf ("Please insert the numbers: n"); for (i=0; i<SIZE; i++) { scanf ("%d", &array[i]); } printf ("The numbers before: n"); print. List(array, SIZE); quick. Sort (array, 0, SIZE-1); printf ("The sorted numbers: n"); print. List(array, SIZE); return 0; } 12

Auxiliary Functions int choose. Pivot(int start_index, int end_index) { return (end_index); } void swap(int *x, int *y) { int temp=*x; *x=*y; *y=temp; } void print. List(int list[], int size) { int i; for (i=0; i<size; i++) { printf ("%d ", list[i]); } printf ("n"); } 13

Sorting strings • Similar to numbers we can sort strings according to their lexicographical order. • What should we change for that? – Instead of comparing two numbers we should compare two strings according to their lexicographical order – Handling strings in input/printing etc.

Changing the comparison • From (numbers): while (i<=j) { while ((i<=end_index) &&(list[i]<=pivot_value)) i++; while ((j>=start_index) && (list[j]>pivot_value)) j--; if (i<j) swap(&list[i], &list[j]); }

Changing the comparison • To (strings): while (i<=j) { while ((i<=end_index) &&(strcmp(list[i], pivot_value)<=0)) i++; while ((j>=start_index) && (strcmp(list[j], pivot_value)>0)) j--; if (i<j) swap(list[i], list[j]); } Now each element is a string, so we don’t need the ‘&’ Reminder: strcmp gets two strings and returns 0 if they are identical. Otherwise, it returns a negative or positive number if the first or second string appears first in lexicographical order, respectively.

The new Partition int partition (char list[][SIZE], int start_index, int end_index) { int i, j; int pivot_index=choose. Pivot(start_index, end_index); char pivot_string[SIZE]=""; strcpy(pivot_string, list[pivot_index]); swap(list[start_index], list[pivot_index]); i=start_index+1; j=end_index; while (i<=j) { while ((i<=end_index) &&(strcmp(list[i], pivot_string)<=0)) i++; while ((j>=start_index) && (strcmp(list[j], pivot_string)>0)) j--; if (i<j) swap(list[i], list[j]); } swap(list[start_index], list[j]); pivot_index=j; return pivot_index; } 17

main int main() { char list[NUM][SIZE]={""}; int i; printf ("Please insert the strings: n"); for (i=0; i<NUM; i++) { read. String(list[i], SIZE-1); } printf ("The strings before sorting: n"); print. List(list, NUM); quick. Sort (list, 0, NUM-1); printf ("The sorted strings: n"); print. List(list, NUM); return 0; } 18

Auxiliary Functions void read. String(char string[], int size) { int i=0; char c; scanf("%c", &c); while ((c!='n')&&(i<size)) { string[i]=c; i++; scanf("%c", &c); } string[i]=''; } void swap(char x[], char y[]) { int i=0; char temp[SIZE]=""; strcpy(temp, x); strcpy(x, y); strcpy(y, temp); } 19

Insertion Sort • Another example for sorting algorithm is Insertion Sort: – In average, It is less efficient as compared to Quick Sort. – For small lists it is quicker as compared to other algorithms. – Many people perform similar algorithm when sorting elements (cards etc. ) • We will explain this algorithm in class while you will implement it in HW…

Insertion Sort • The idea behind the algorithm: • Go through the list from the first element and at each step put the i’th elements in its position in the sorted list that contain 1, …, i -1, i elements. • At this stage, the first i elements are sorted. • Stopping in i=n, we have a sorted list.

Example

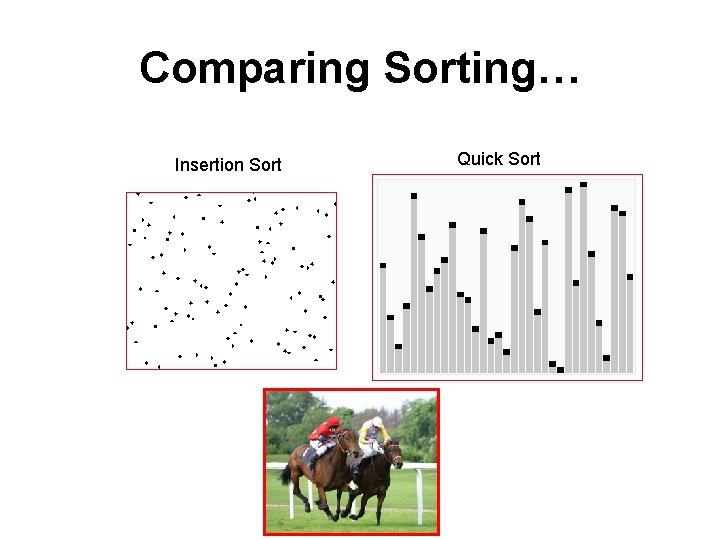
Comparing Sorting… Insertion Sort Quick Sort

Complexity of algorithms • We can compare the two algorithms in respect to time complexity. • Here we shall introduce only the highlights of that complexity analysis.

Insertion Sort • Best case scenario: – The list is already sorted. In this case, the i’th element is compared only to i-1 element. Thus, we have ~n comparisons. • Worst case scenario: – The list is sorted backwards. In this case the i’th element needs to be shifted all the way back to the start of the list. – Quadratic complexity: 1+2+3+. . +n-1=~n 2 • Average case (without proving): – It also takes ~n 2 operations.

Quick Sort • The partition step takes ~n operations (we go through the list and change the location of the elements according to the pivot). • Best case scenario: – In each partition, we divide the list into almost equal size lists (each containing (k-1)/2 elements). That means we have ~log(n) partitions. Therefore total time complexity is ~n*log(n).

Quick Sort • Worst case scenario: – In each step we divide the list of k elements (starting from k=n) into k-1 and 1 elements. In this case each step takes ~n-k operations. Thus we have: • (n-1)+(n-2)+(n-3)+…+1=~n 2.

Quick Sort • Average case (without proving): – In this case it takes ~1. 39 n*log(n) operations. • Thus, Quick Sort is faster than Insertion Sort on average. • In fact, any algorithm for sorting n elements using pairwise comparisons cannot do it faster than ~n*log(n) in the average case.

Selection Sort • Selection Sort is another sorting algorithm which is relatively simple: • Given a list of elements: – Find the minimum and swap it with the first element. – Repeat it for the remainder of the list (now swapping with the 2 nd, 3 rd element etc. ).

Selection Sort - Example

Complexity analysis • In each step we look for the minimal element – thus we go through all the remaining elements. This is done n times. • Time complexity is: (n)+(n-1)+(n-2)+…+1=~n 2 • This is done on all inputs, therefore best case=worst case=average case.

And the winner is… Insertion Sort Quick Sort Selection Sort