Sorting networks Efficient Parallel Algorithms COMP 308 Sorting

Sorting networks Efficient Parallel Algorithms COMP 308

Sorting networks n Today, we investigate sorting algorithms based on a comparison network model of computation in which many comparison operations can be performed simultaneously n Sorting networks are comparison networks that always sort their inputs. They are comprised solely of wires and comparators

Comparator n. A comparator is a device with two inputs, x and y, and outputs, x’ and y’, that performs the following function: x’= min (x, y) y’= max (x, y) x y COMPARATOR x’ 7 3 y’ 3 7

Wire We shall assume that each comparator operates in O(1) time. In other words, we assume that the time between the appearance of the input values x and y and the production of the output values x’ and y’ is a constant. n A wire transmits a value from place to place. Wires can connect the output of one comparator with the input of another, but otherwise they are either network input wires or network output wires. n

n We shall speak of the input sequence <a 1, a 2, …, an> and the output sequence <b 1, b 2, …, bn>, referring to the values on the input and output wires. n A sorting network is a comparison network for which the output sequence is monotonically increasing (that is b 1 b 2 … bn) for every input sequence.

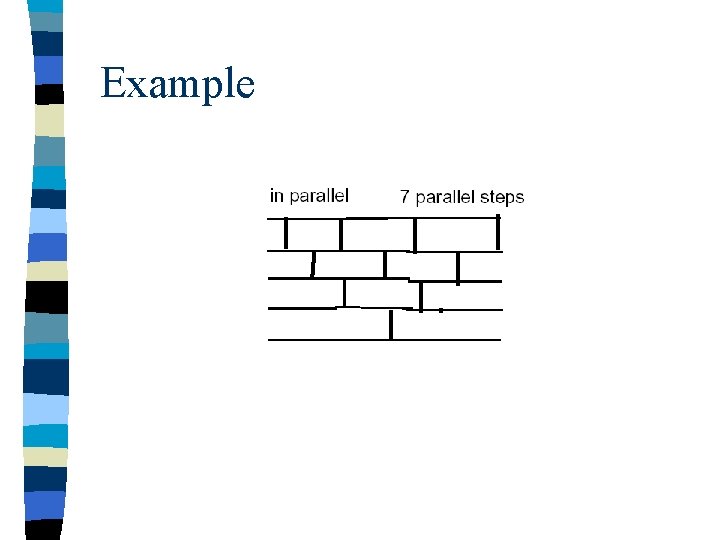
Example

The zero-one principle says that if a sorting networks correctly when each input is drawn from the set {0, 1}, then it works correctly on arbitrary input numbers. n Once we constructed a sorting network and proved that it can sort all zero-one sequences, we shall appeal to the zero-one principle to show that it properly sorts sequences of arbitrary values. n

The proof of the zero-one principle relies on the notion of a monotonically increasing function. n Lemma If a comparison network transforms the input sequence a = <a 1, a 2, …, an> into the output sequence b = <b 1, b 2, …, bn>, then for any monotonically increasing function f, the network transforms the input sequence f(a) = <f(a 1), f(a 2), …, f(an)> into sequence f(b) = <f(b 1), f(b 2), …, f(bn)>.

Proof. We shall first prove the claim that if f is monotonically increasing function, then a single comparator with inputs f(x) and f(y) produces outputs f(min(x, y)) and f(max(x, y)). We shall then use induction to prove the lemma n To prove the claim, consider a comparator whose input values are x and y. The upper output of the comparator is min(x, y) and the lower output is max(x, y). Suppose now apply f(x) and f(y) to the inputs of the comparator as is shown on the figure n f(x) min(f(x), f(y))=f(min(x, y)) f(y) max(f(x), f(y))=f(max(x, y))

n f(x) min(f(x), f(y))=f(min(x, y)) f(y) max(f(x), f(y))=f(max(x, y)) Since f is monotonically increasing x y imply f(x) f(y). Consequently, we ha the identities: min(f(x), f(y))=f(min(x, y)) max(f(x), f(y))=f(max(x, y)) n We can use induction on the depth of each wire in a general comparison network to prove a stronger result than the statement of the lemma: – If a wire assumes the value ai when the input sequence a is applied to the network, then it assumes the value f(ai) when the input sequence f(a) is applied.

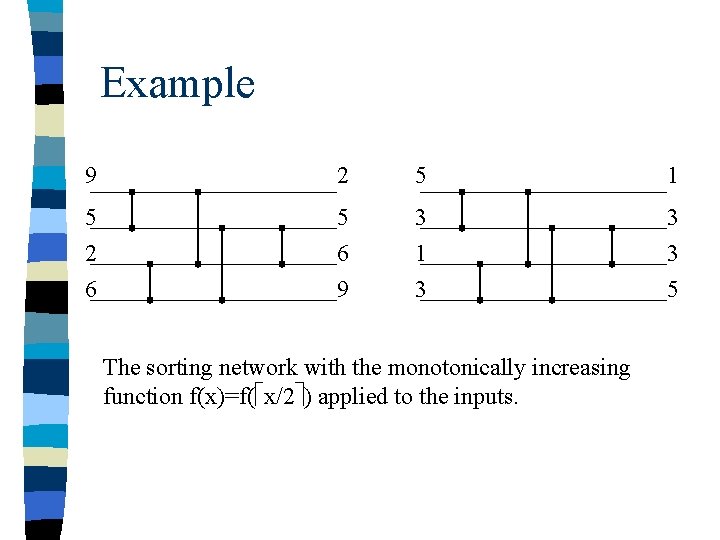
Example 9 2 5 1 5 2 5 6 3 1 3 3 6 9 3 5 The sorting network with the monotonically increasing function f(x)=f( x/2 ) applied to the inputs.

Theorem. (0 -1 principle) If comparison network with n inputs sorts all 2 n possible sequences of 0’s and 1’s correctly, then it sorts all sequences of arbitrary numbers correctly. Proof. Suppose for the purpose of contradiction that the network sorts all zero-one sequences, but there exists a sequence of arbitrary numbers that the network does not correctly sort. That is, there exists an input sequence a = <a 1, a 2, …, an> containing elements ai and aj such that ai < aj, but network place aj before ai in the output sequence. n

We define monotonically increasing function f as 0 if x ai, f(x) = 1 if x>ai n Since the network places aj before ai in the output sequence when <a 1, a 2, …, an> is input, it follows from Lemma that it place f(aj) before f(ai) in the output sequence when <f(a 1), f(a 2), …, f(an)> is input. n But since f(aj)=1 and f(ai)=0, we obtain the contradiction that the network fails to sort the zero-one sequence <f(a 1), f(a 2), …, f(an)> correctly. n