External Sort ExternalMemory Sorting n Externalmemory algorithms n

External Sort

External-Memory Sorting n External-memory algorithms n n External-memory sorting n n When data do not fit in main-memory Rough idea: sort pieces that fit in main-memory and then “merge” them Main-memory merge sort: n The main part of the algorithm is Merge 2

Main-Memory Merge Sort Merge-Sort(A) 01 if length(A) > 1 then 02 Copy the first half of A into array A 1 03 Copy the second half of A into array A 2 04 Merge-Sort(A 1) 05 Merge-Sort(A 2) 06 Merge(A, A 1, A 2) n Divide Conquer Combine Running time for Merge sort: O(nlogn) 3

1. 2. 3. Read the 1 st 250 records of Run 1 from scratch disk into Buffer 1 Read the 1 st 250 records of Run 2 into Buffer 2 Merge buffers 1 and 2 into Buffer 3. As soon as buffer 3 gets full, - write it (250 records) on scratch disk, - empty buffer 3. - continue merging the remaining records left in buffers 1 and 2 Note that this process will terminate when buffer 3 gets full 2 times and 2 times writing it on scratch disk is carried on. 9

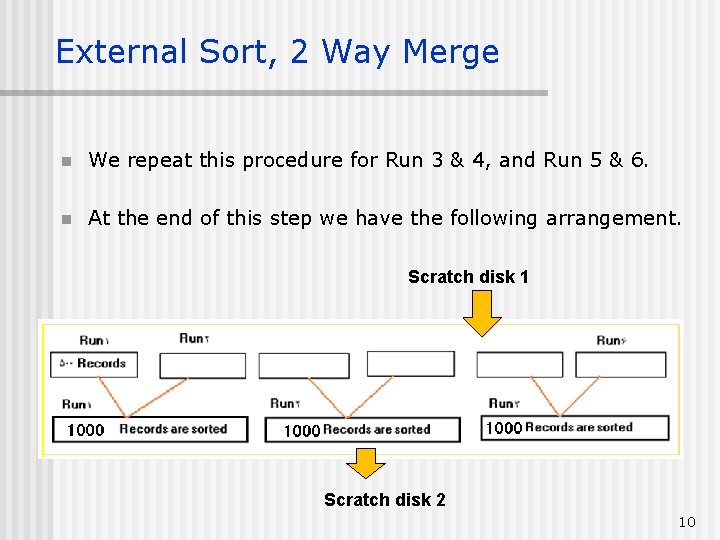
External Sort, 2 Way Merge n We repeat this procedure for Run 3 & 4, and Run 5 & 6. n At the end of this step we have the following arrangement. Scratch disk 1 Scratch disk 2 10

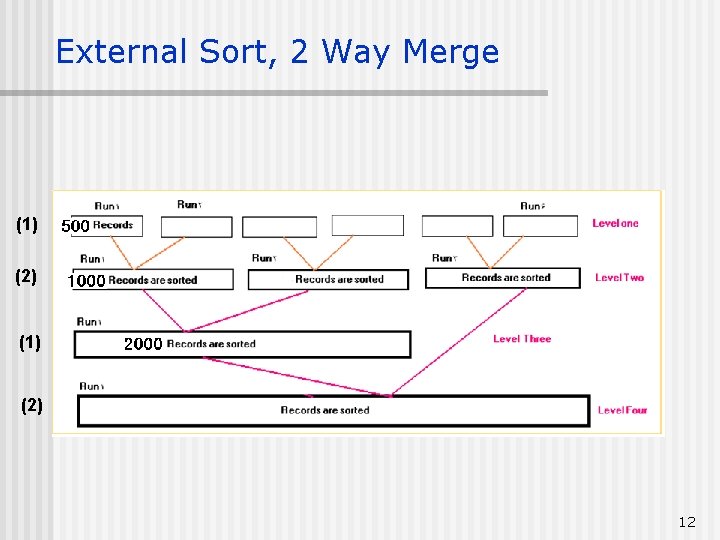
External Sort, 2 Way Merge This process of n n n n coping the 1 st 250 records from Run 1 (in scratch disk 1) into Buffer 1, and the 1 st 250 records from Run 2 (in scratch disk 1) into Buffer 2, Merge them into Buffer 3, When buffer 3 gets full, Write buffer 3 on Scratch disk 2 Empty Buffer 3 Continue merging the remaining records in buffers 1 and 2 into buffer 3. When buffer 3 gets full, Write buffer 3 on Scratch disk 2 Empty Buffer 3 Is continued until all Runs from scratch disk 1 in this level are merged into New Runs. Note that the number of Runs in each level is at most ½ of the number of Runs in its previous level. 11

External Sort, 2 Way Merge (1) (2) 12

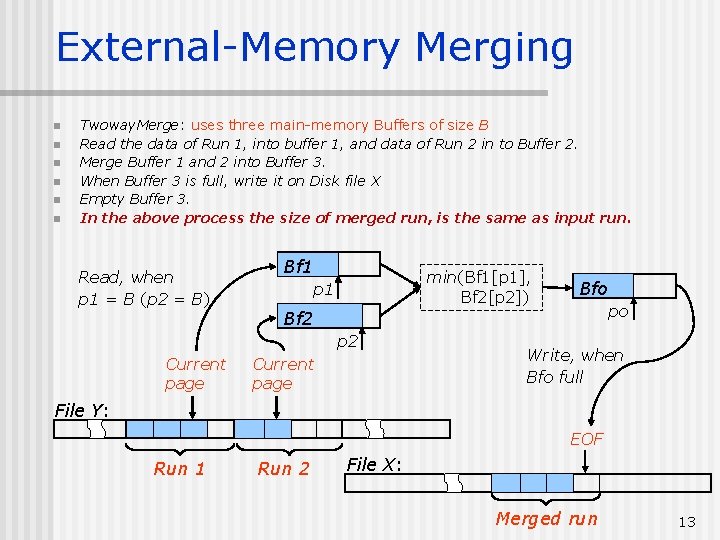
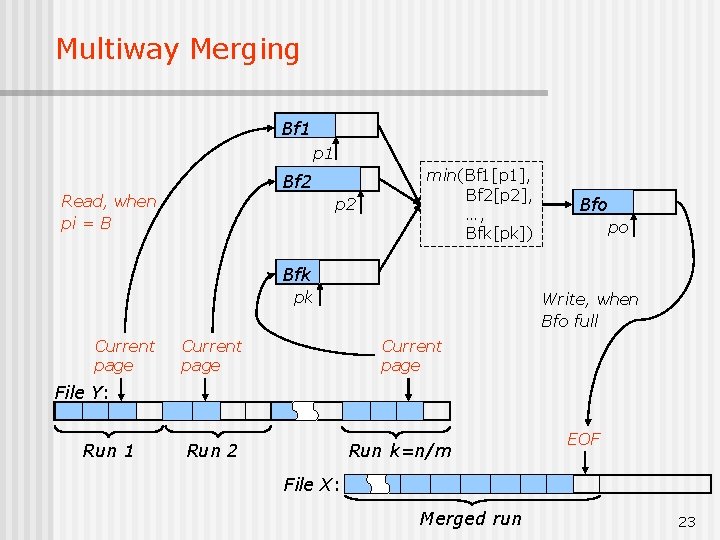
External-Memory Merging n n n Twoway. Merge: uses three main-memory Buffers of size B Read the data of Run 1, into buffer 1, and data of Run 2 in to Buffer 2. Merge Buffer 1 and 2 into Buffer 3. When Buffer 3 is full, write it on Disk file X Empty Buffer 3. In the above process the size of merged run, is the same as input run. Read, when p 1 = B (p 2 = B) Bf 1 min(Bf 1[p 1], Bf 2[p 2]) p 1 po Bf 2 p 2 Current page Bfo Current page Write, when Bfo full File Y: EOF Run 1 Run 2 File X: Merged run 13

Time complexity analysis: Assumptions n Assumptions and notation: n Disk page size: B: The number of data elements (records) in one page of disk. n Data file size: N = n. B // n: Number of disk pages • n = N/B n Available main memory: • M elements, m = M/B pages 14

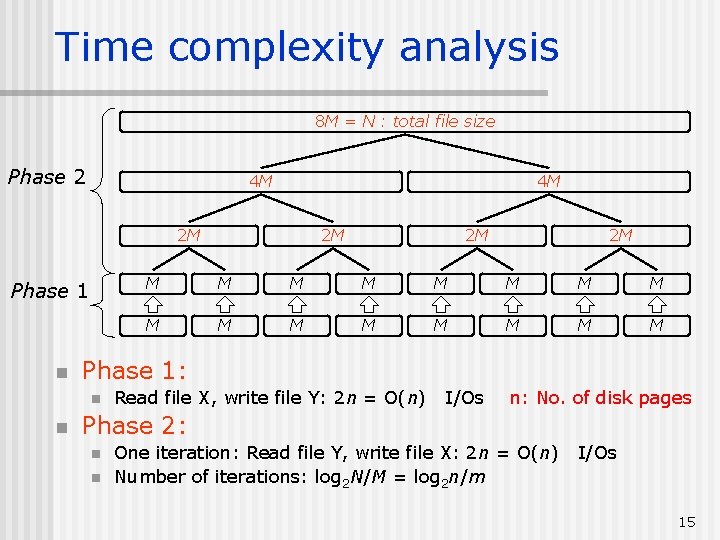
Time complexity analysis 8 M = N : total file size Phase 2 4 M 4 M 2 M Phase 1 n 2 M 2 M M M M M Phase 1: n n 2 M Read file X, write file Y: 2 n = O(n) I/Os n: No. of disk pages Phase 2: n n One iteration: Read file Y, write file X: 2 n = O(n) Number of iterations: log 2 N/M = log 2 n/m I/Os 15

Time complexity analysis : Conclusions n Total running time of 2 -way externalmemory merge sort: O(n log 2 n/m) n Can we obtain better running time ! 16

Time complexity analysis : Conclusions n Can we obtain better running time ! n We test the following: n n Phase 1 uses all available memory Phase 2 uses just 3 pages out of m available pages !!! 17

External Sort, K Way Merge 18

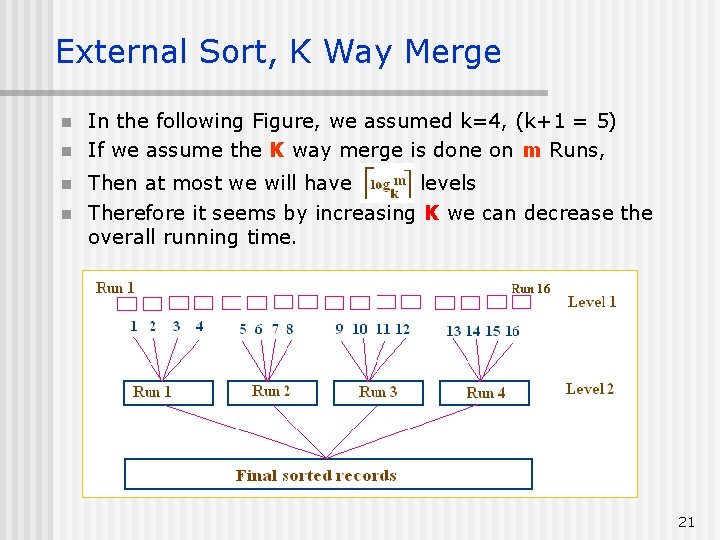
External Sort, K Way Merge n n In the following Figure, we assumed k=4, (k+1 = 5) If we assume the K way merge is done on m Runs, Then at most we will have levels Therefore it seems by increasing K we can decrease the overall running time. 21

Multiway Merging Bf 1 p 1 Bf 2 Read, when pi = B p 2 min(Bf 1[p 1], Bf 2[p 2], …, Bfk[pk]) Bfo po Bfk pk Current page Write, when Bfo full Current page File Y: Run 1 Run 2 Run k=n/m EOF File X: Merged run 23

Multiway, (k way) Merging n Here we assume we have k+1 buffers (buffer 0, 1, . . , k) in the main memory each having the size of n/m elements. n We sort the data in each buffers 1~K, and Repeatedly find the min elements in these k buffers and put it in buffer 0. n Any time that buffer 0 gets filed in, we write it on the end of file X and empty buffer 0, for the next bulk of sorted data. n This process is repeated until all sorted data is written in file X. 24

General Multiway Merge Sort n What if a file is very large or memory is small? n General multiway merge sort: n Phase 1: the same (do internal sorts) n Phase 2: do as many iterations of merging as necessary until only one run remains Each iteration repeatedly calls Multiway. Merge(Y, X) to merge groups of m-1 runs until the end of file Y is reached. 27

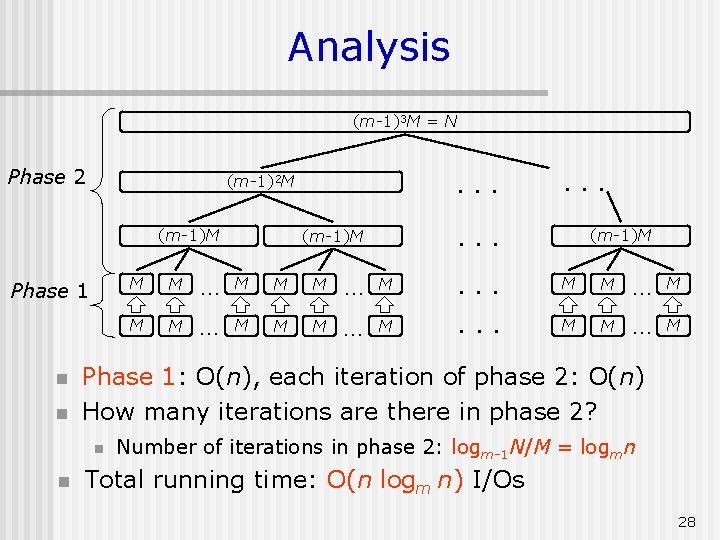
Analysis (m-1)3 M = N Phase 2 (m-1)M Phase 1 n n . . . (m-1)M M M … M . . . M M … M Phase 1: O(n), each iteration of phase 2: O(n) How many iterations are there in phase 2? n n . . . (m-1)2 M Number of iterations in phase 2: logm-1 N/M = logmn Total running time: O(n logm n) I/Os 28

Conclusions B: number of records in one page of disk. n: Number of disk pages M: available main memory (in number of records), m = M/B pages n Total running time of 2 -way external-memory merge sort: O(n log 2 n/m) n External sorting can be done in O(n logm n) I/O operations for any n n This is asymptotically optimal 29

End of sorting algorithms 30

31