CHAPTER 6 SORTING ALGORITHMS Sorting Definition sorting is























![Another Coding example void bubble (int array[], int size, int select) { int i, Another Coding example void bubble (int array[], int size, int select) { int i,](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-41.jpg)



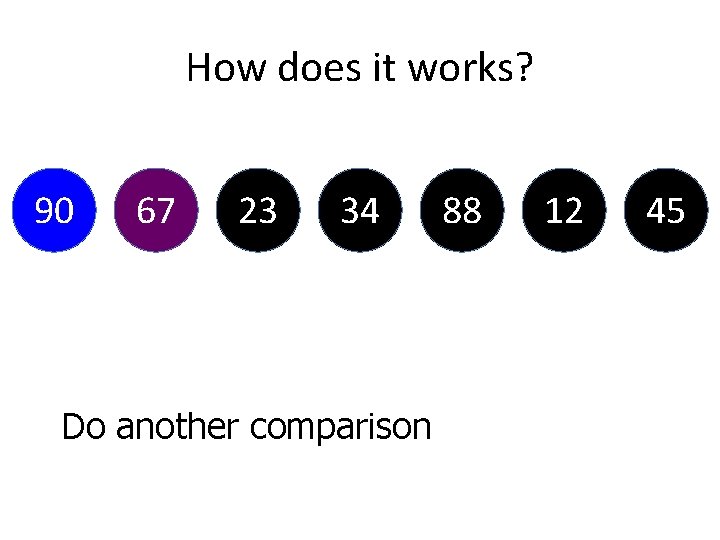
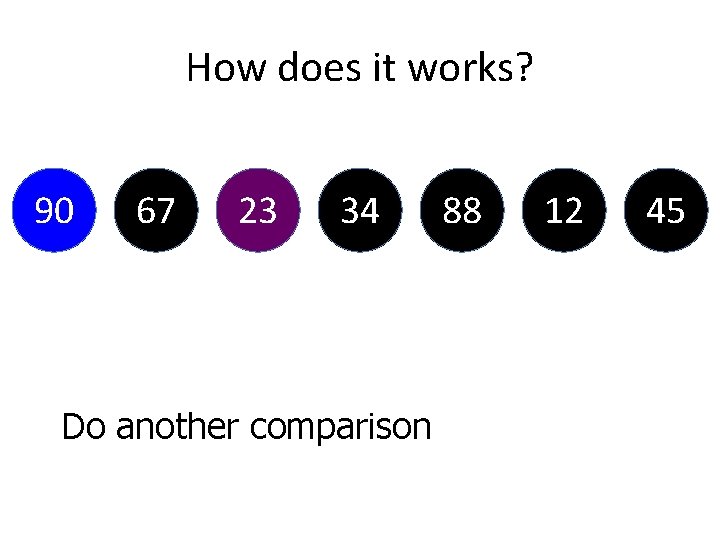
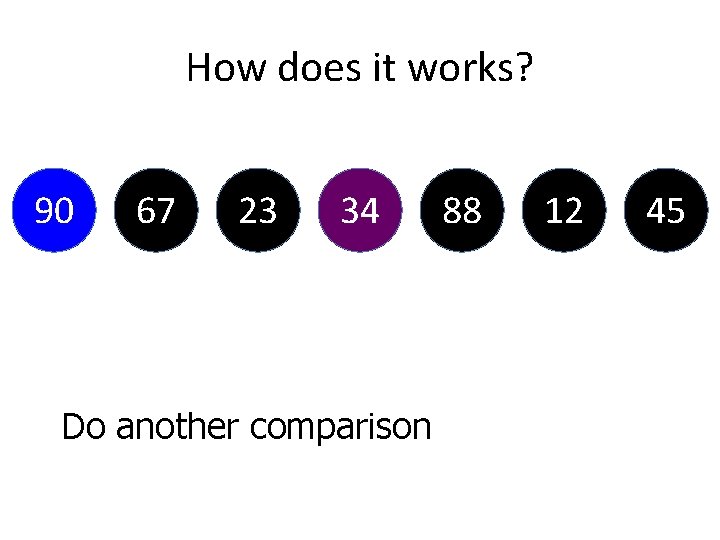
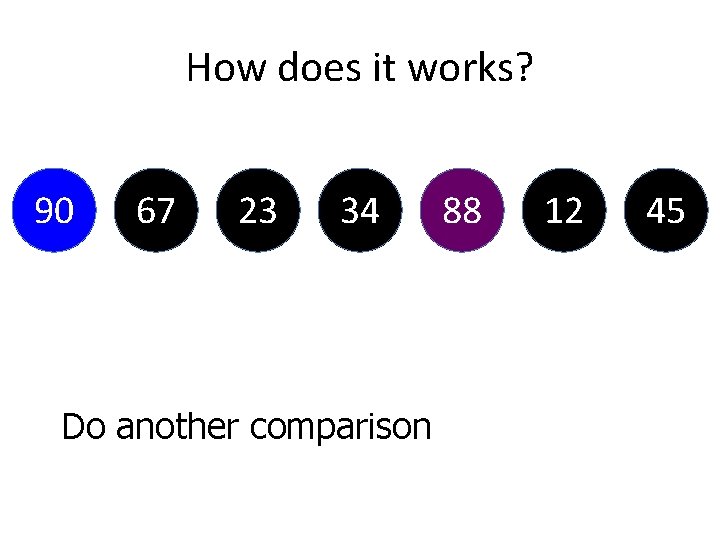
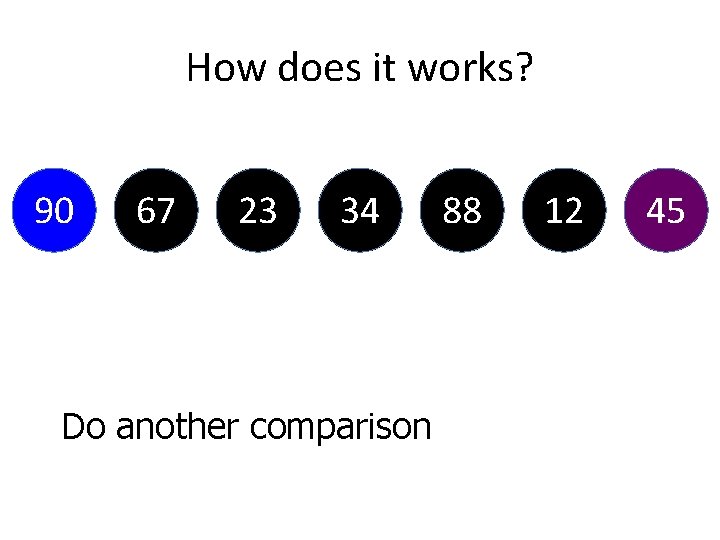


















![Algorithm for Selection Sort Coding for(a=0; a<size; a++) { smallest=a; for(b=a+1; b<size; b++) if(data[b]<data[smallest]) Algorithm for Selection Sort Coding for(a=0; a<size; a++) { smallest=a; for(b=a+1; b<size; b++) if(data[b]<data[smallest])](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-75.jpg)
![Another Style of Coding void selection(int array[], int size, int select) { int i, Another Style of Coding void selection(int array[], int size, int select) { int i,](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-76.jpg)










![Step of Develop Insertion Sort C++ Code If temp is smaller than arrlist[previously], then Step of Develop Insertion Sort C++ Code If temp is smaller than arrlist[previously], then](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-99.jpg)


![Coding void insertion(int array[], int size, int select) { int i, j, temp; for(i=1; Coding void insertion(int array[], int size, int select) { int i, j, temp; for(i=1;](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-102.jpg)







![On Code 34 67 23 90 88 a[left] @ a[0] = 34 12 45 On Code 34 67 23 90 88 a[left] @ a[0] = 34 12 45](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-130.jpg)

![Phase 2 Quicksort Code At first, a[left] which is a[0] will be compared with Phase 2 Quicksort Code At first, a[left] which is a[0] will be compared with](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-132.jpg)
![On Code 34 67 23 90 88 12 while (a[left] < pivot) left++; while On Code 34 67 23 90 88 12 while (a[left] < pivot) left++; while](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-134.jpg)
![On Code 34 67 23 90 88 12 while (a[0] < 34) left++; - On Code 34 67 23 90 88 12 while (a[0] < 34) left++; -](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-135.jpg)

![On Code 34 67 23 90 88 12 if (left < right && a[left] On Code 34 67 23 90 88 12 if (left < right && a[left]](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-137.jpg)
![On Code 34 67 23 90 88 if ( 0< 5 && a[0] != On Code 34 67 23 90 88 if ( 0< 5 && a[0] !=](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-138.jpg)
![On Code 12 67 23 90 88 if ( 0< 5 && a[0] != On Code 12 67 23 90 88 if ( 0< 5 && a[0] !=](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-139.jpg)


![Round 2 12 67 23 90 88 34 45 while (a[0] < 34) left++; Round 2 12 67 23 90 88 34 45 while (a[0] < 34) left++;](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-142.jpg)
![Round 2 12 34 23 90 88 if ( 1< 5 && a[1] != Round 2 12 34 23 90 88 if ( 1< 5 && a[1] !=](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-143.jpg)
![Round 3 12 34 23 90 88 67 while (a[1] < 34) left++; - Round 3 12 34 23 90 88 67 while (a[1] < 34) left++; -](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-144.jpg)
![Round 3 12 23 34 90 88 if ( 1< 2 && a[1] != Round 3 12 23 34 90 88 if ( 1< 2 && a[1] !=](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-145.jpg)
![Round 4 12 23 34 90 88 67 while (a[1] < 34) left++; - Round 4 12 23 34 90 88 67 while (a[1] < 34) left++; -](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-146.jpg)























![Example 34 67 23 90 88 12 45 First mergesort is ([ourarray], 0, 3) Example 34 67 23 90 88 12 45 First mergesort is ([ourarray], 0, 3)](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-175.jpg)















- Slides: 190

CHAPTER 6 SORTING ALGORITHMS

Sorting • Definition: sorting is the process of sequencing or arranging a list of data items – According to some order – Ascending/descending • Main purpose: – To improve the search or access time – Without sorting, it will generally take a longer time to access information in a file or database esp. if the database is large. – Imagine, telephone directory without sorting.

Why we need to sort stuff? • Let say you have a list of phone numbers of your friends • You can easily find any numbers if the list are small • But imagine you have hundreds of friends • So, you begin to sort it according to alphabetic or any order

Sorting 1. 2. 3. 4. 5. 6. Bubble sort Selection sort Insertion sort Quicksort Mergesort Heapsort optional Faster – for large data

Sorting Algorithms and Average Case Number of Comparisons Simple Sorts –Bubble Sort –Straight Selection –Insertion Sort O(N 2) Sort More Complex Sorts –Quick Sort –Merge Sort –Heap Sort O(N*log N) There are several sorts that are relatively easy to code. These are considered to be "simple sorts" and generally have bad run time O(n 2). 5

Big-O notation • One way to describe the efficiency of an algorithm is with Big-O notation (O), which indicates how hard an algorithm may have to work to solve a problem. • For searching and sorting algorithm s, Big-O describes how the amount of effort of a particular algorithm varies depending on how many elements are in the data. • An O(n) algorithm is referred to as having a linear runtime.

Complexity of sorting algorithm • Big-O used to measure the computational complexity of a particular sort based on: – The number of iterations – Comparisons – Assignment statements etc • The measure is relative to the number of data items(n) to be sorted. • Thus, the complexity of a sorting algorithm measures the running time as a function of the number of data items to be sorted.

Classification of complexity (continue) Sorting algorithms Insertion sort Selection sort Bubble sort Quick sort Merge sort Big-O O(n 2) Worst case: O(n 2) Average case: O(nlogn)

BUBBLE SORT IMPLEMENTATION

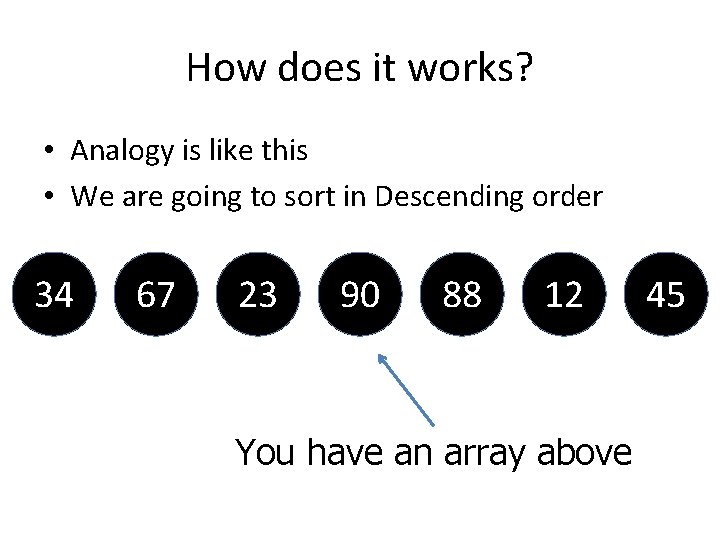
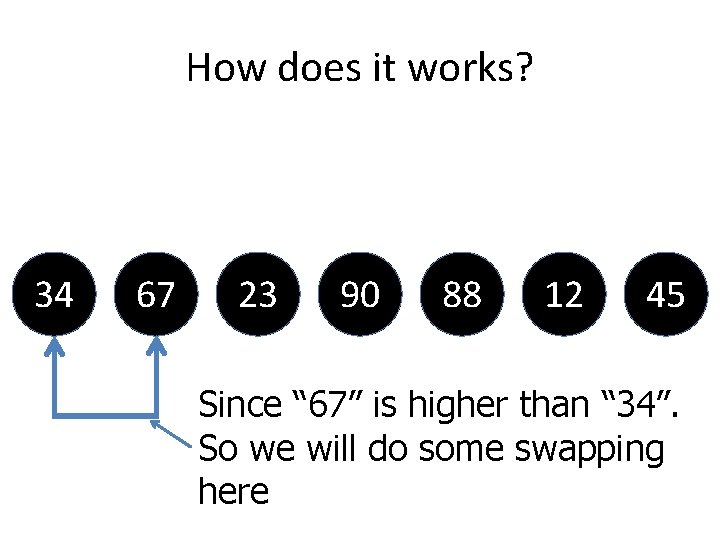
How does it works? • Analogy is like this • We are going to sort in Descending order 34 67 23 90 88 12 You have an array above 45

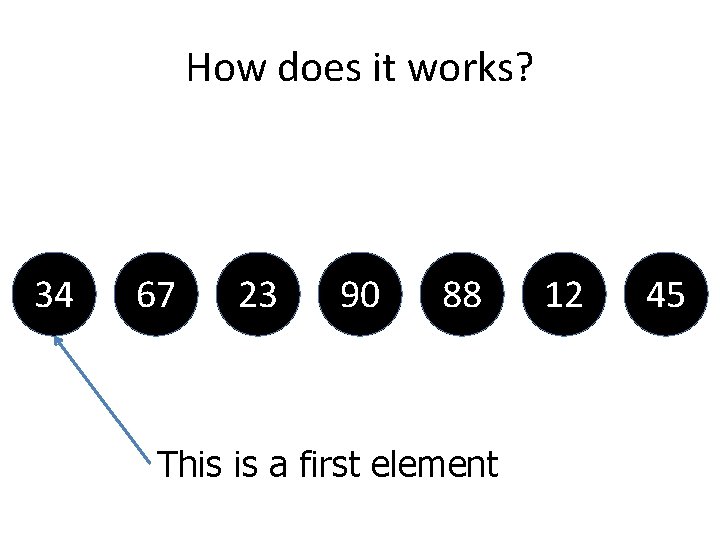
How does it works? 34 67 23 90 88 This is a first element 12 45

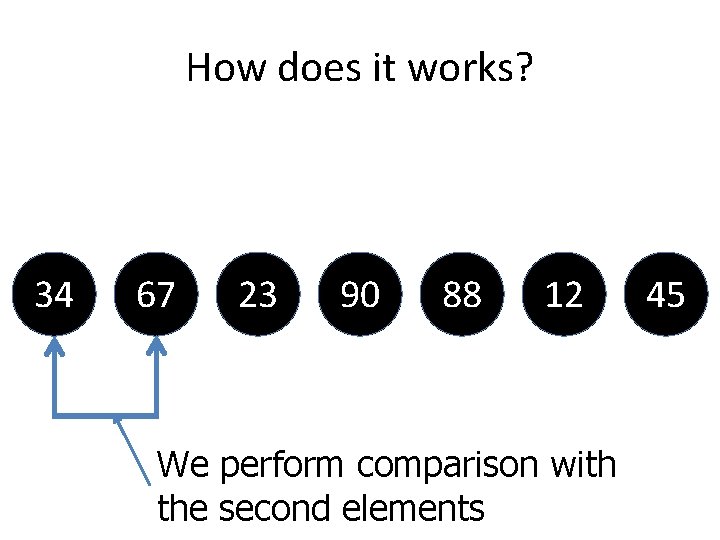
How does it works? 34 67 23 90 88 12 We perform comparison with the second elements 45

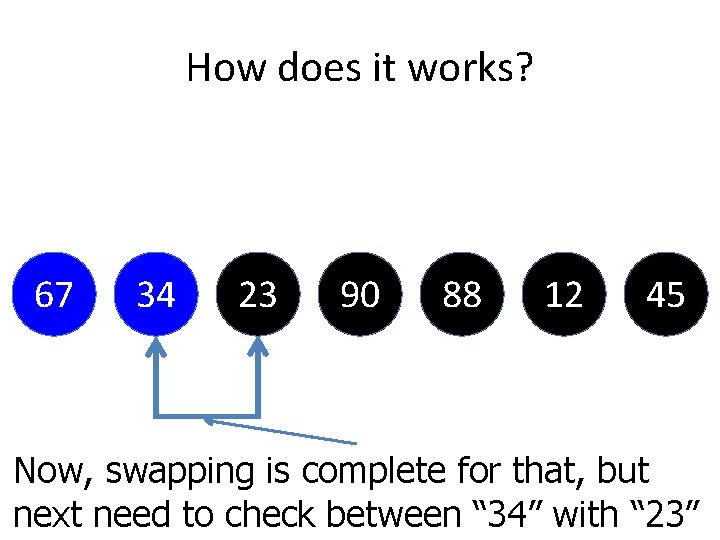
How does it works? 34 67 23 90 88 12 45 Since “ 67” is higher than “ 34”. So we will do some swapping here

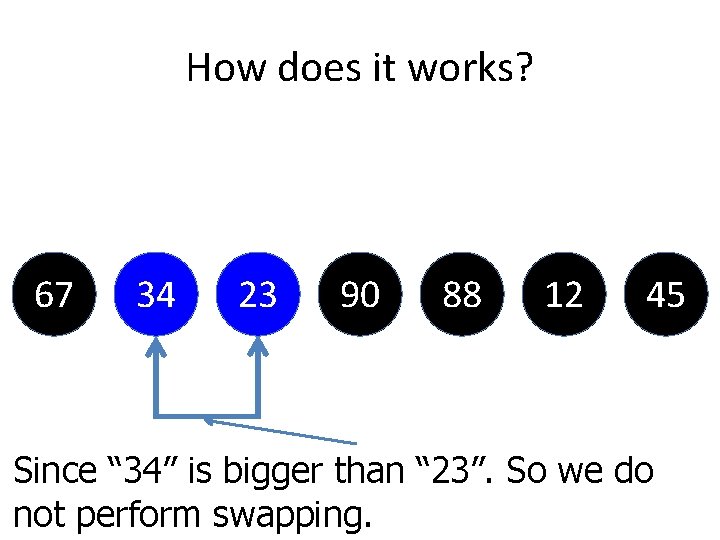
How does it works? 67 34 23 90 88 12 45 Now, swapping is complete for that, but next need to check between “ 34” with “ 23”

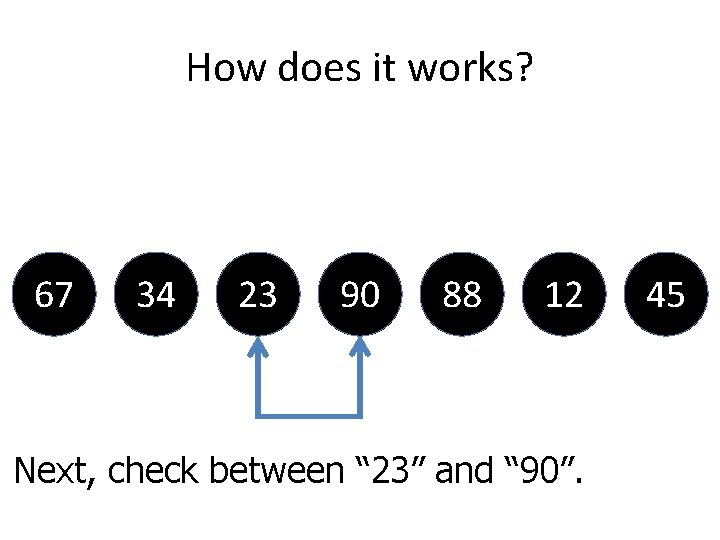
How does it works? 67 34 23 90 88 12 45 Since “ 34” is bigger than “ 23”. So we do not perform swapping.

How does it works? 67 34 23 90 88 12 Next, check between “ 23” and “ 90”. 45

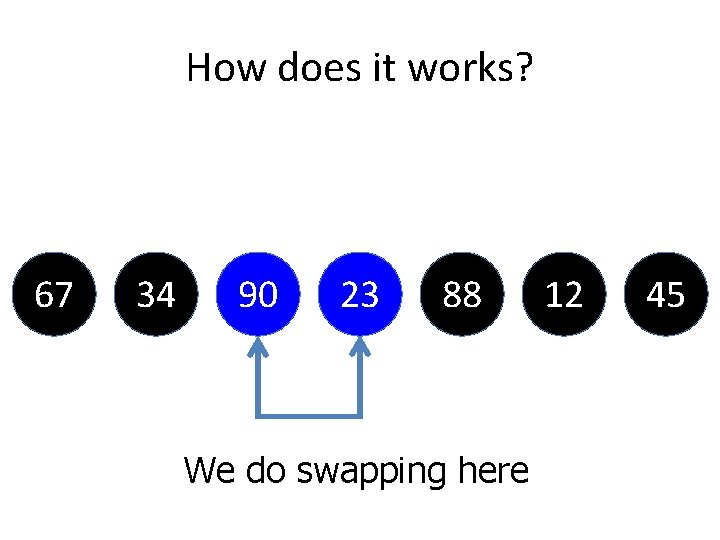
How does it works? 67 34 90 23 88 We do swapping here 12 45

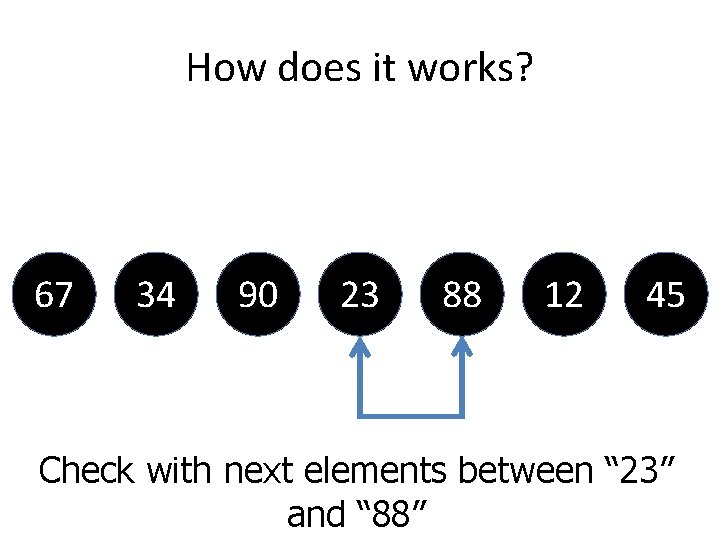
How does it works? 67 34 90 23 88 12 45 Check with next elements between “ 23” and “ 88”

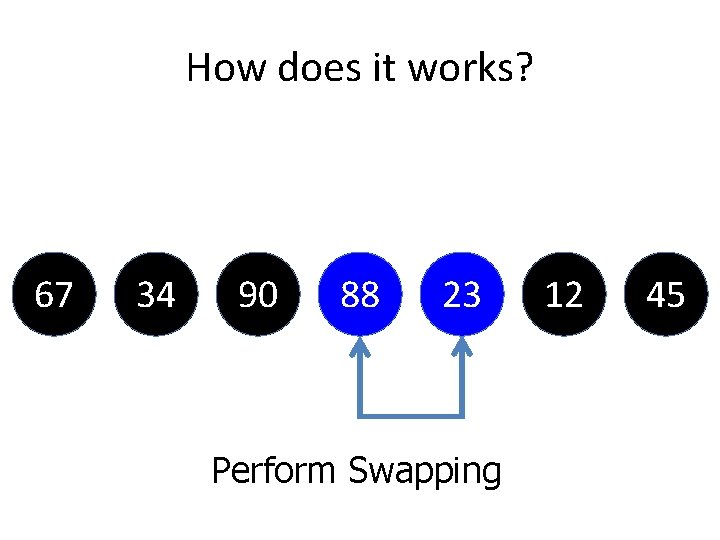
How does it works? 67 34 90 88 23 Perform Swapping 12 45

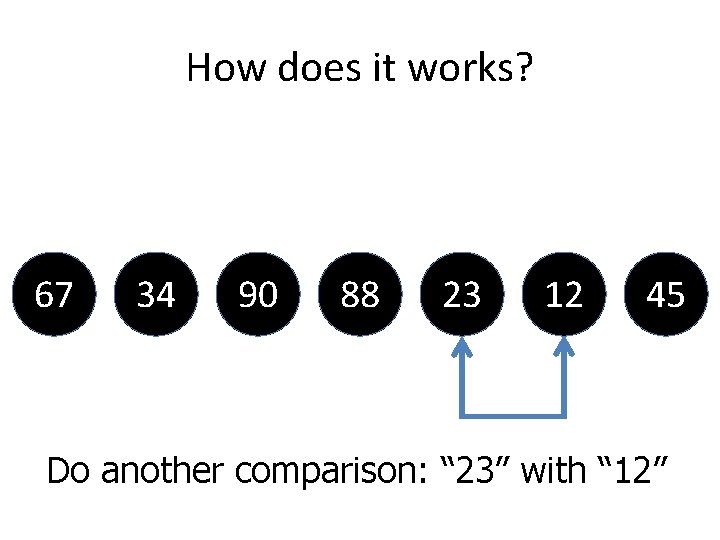
How does it works? 67 34 90 88 23 12 45 Do another comparison: “ 23” with “ 12”

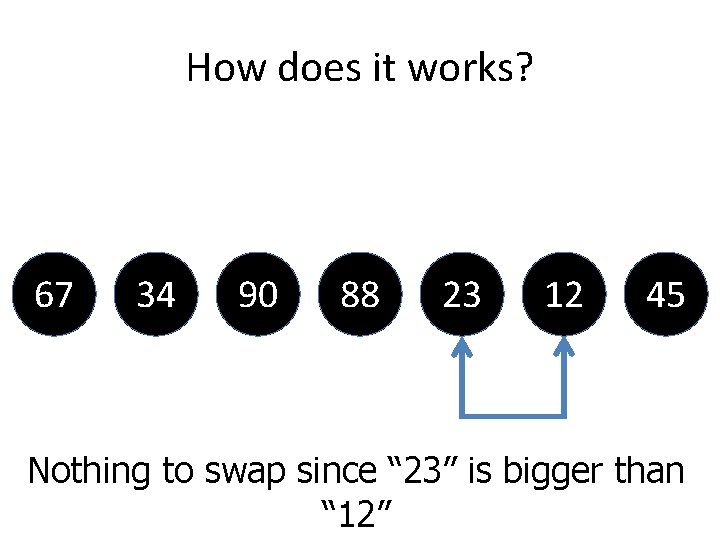
How does it works? 67 34 90 88 23 12 45 Nothing to swap since “ 23” is bigger than “ 12”

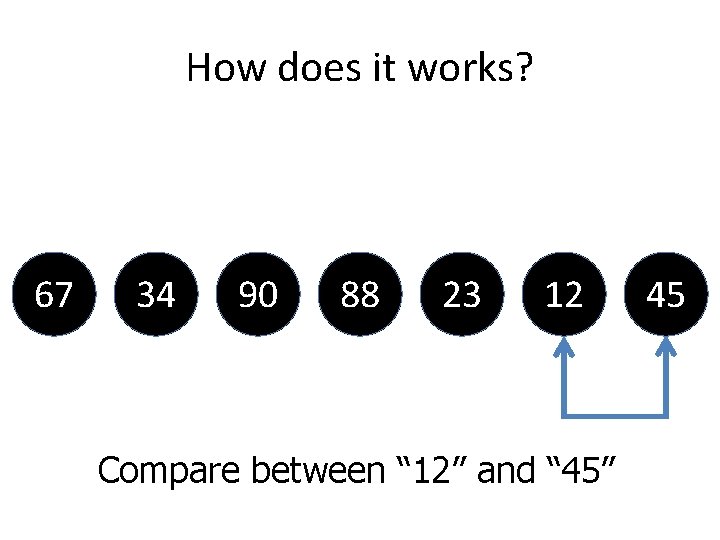
How does it works? 67 34 90 88 23 12 Compare between “ 12” and “ 45” 45

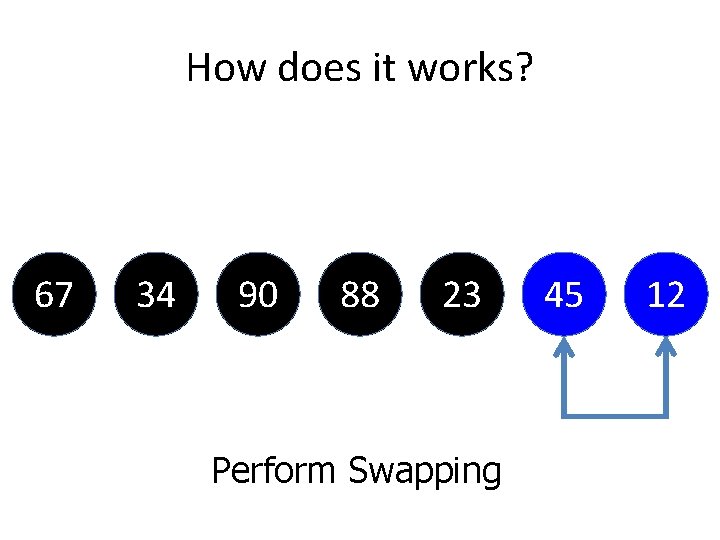
How does it works? 67 34 90 88 23 Perform Swapping 45 12

How does it works? 67 34 90 88 23 Done 1 st Pass 45 12

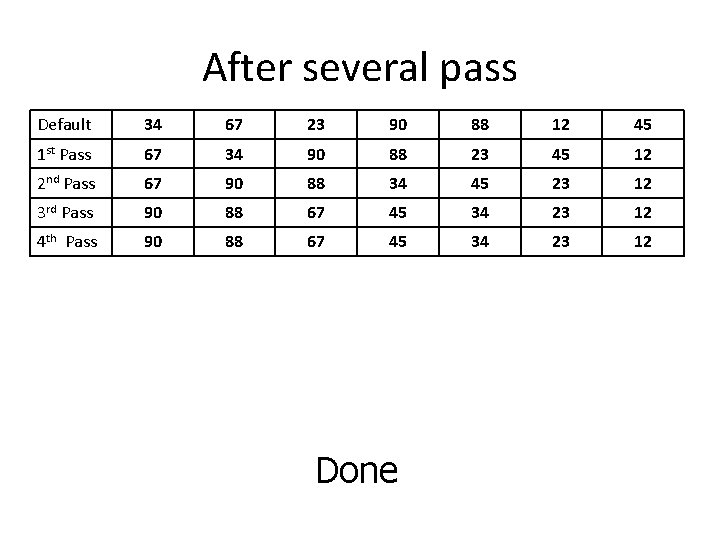
After several pass Default 34 67 23 90 88 12 45 1 st Pass 67 34 90 88 23 45 12 2 nd Pass 67 90 88 34 45 23 12 3 rd Pass 90 88 67 45 34 23 12 4 th Pass 90 88 67 45 34 23 12 Done

Bubble sort • The bubble sort repeatedly compares adjacent elements of an array, starting with the first and second elements, and swapping them if they are out of order. • After the first and second elements are compared, the second and third elements are compared, and swapped if they are out of order. • This process continues until the end of the list is reached.

Bubble sort (continue) • When the end is reached, the bubble sort returns to elements one and two and starts the process all over again. So, when does it stop? The bubble sort knows that it is finished when it examines the entire array and no "swaps" are needed (thus the list is in proper order).

Example 1: Descending order

Example 2: Ascending order Begin : Pass 1: Pass 2: Pass 3: Pass 5 (done): 1 2 3 4 5 6

How to code • Bubble sort involves: – Swapping process – Check with the right element (next element) – Iterate until reach end of array list So, you need to have some sort of “if-else” and “for looping”

First Step of Develop Bubble Sort C++ Code • It must have swapping process. So, how do you swap stuff? • But let us first declare some array and get input and display the input before sorting • We will perform descending order of sorting


First Step of Develop Bubble Sort C++ Code • Now, let us have swapping process • Implement for all elements in an array list

First Step of Develop Bubble Sort C++ Code First, I’ve declared a temporary variable to hold a value that need to be swap.

First Step of Develop Bubble Sort C++ Code Then, a looping “for” to loop all elements for swapping process

First Step of Develop Bubble Sort C++ Code Here, we do some tests - If current element of “I” has smaller value than next element which is “i+1” and i+1 is not 10. We will do swapping process

First Step of Develop Bubble Sort C++ Code • However, the code just swap only once until the end of the array list and the array is still unsorted. Look at the output

Second Step of Develop Bubble Sort C++ Code So, let us modify a bit the process so it can run for each elements to sort

Second Step of Develop Bubble Sort C++ Code In above code, we just add one more loop “for” in order to loop for each element

Final Step Finally, an algorithm code of Bubble Sort
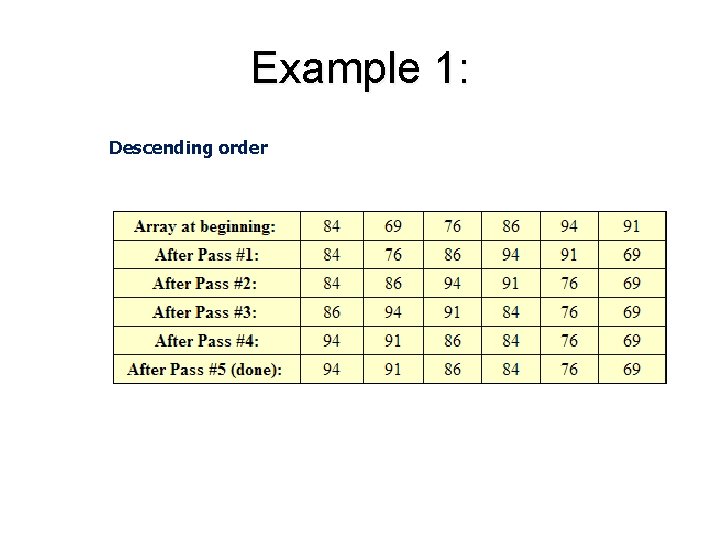
![Another Coding example void bubble int array int size int select int i Another Coding example void bubble (int array[], int size, int select) { int i,](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-41.jpg)
Another Coding example void bubble (int array[], int size, int select) { int i, j, temp; for(i=0; i<size-1; i++) for(j=1; j<size; j++) { if((array[j]<array[j-1])&&(select==1))//ascending order { temp=array[j]; array[j]=array[j-1]; array[j-1]=temp; } else if((array[j]>array[j-1])&&(select==2))//descending order { temp=array[j]; array[j]=array[j-1]; array[j-1]=temp; } } }

Disadvantages of bubble sort • The bubble sort is an easy algorithm to program, but it is slower than many other sorts. • With a bubble sort, it is always necessary to make one final "pass" through the array to check to see that no swaps are made to ensure that the process is finished. • In actuality, the process is finished before this last pass is made.

SELECTION SORT IMPLEMENTATION

How does it works? • We will use the same array. • We are going to sort in Descending order 34 67 23 90 88 12 You have an array above 45

How does it works? 34 67 23 90 88 12 Find the biggest value of elements 45

How does it works? 34 67 23 90 88 12 45 Do comparison with the first element

How does it works? 90 67 23 34 88 12 Perform swapping if the “chosen element” has bigger value than the compared element 45
How does it works? 90 67 23 34 Do another comparison 88 12 45
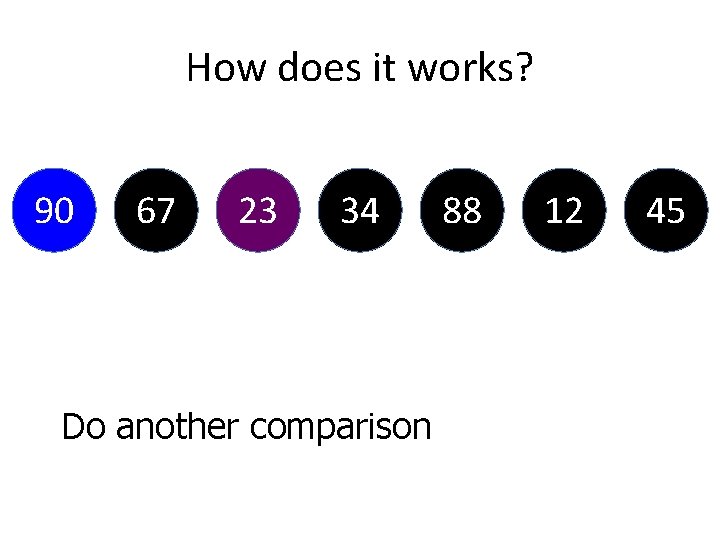
How does it works? 90 67 23 34 Do another comparison 88 12 45
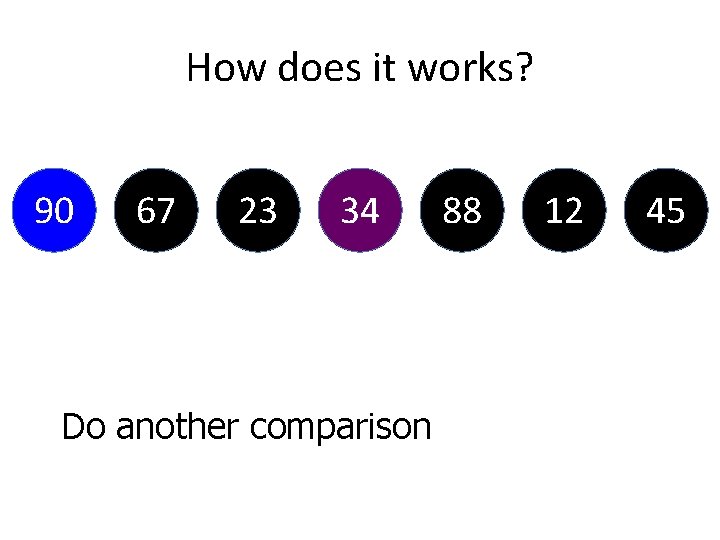
How does it works? 90 67 23 34 Do another comparison 88 12 45
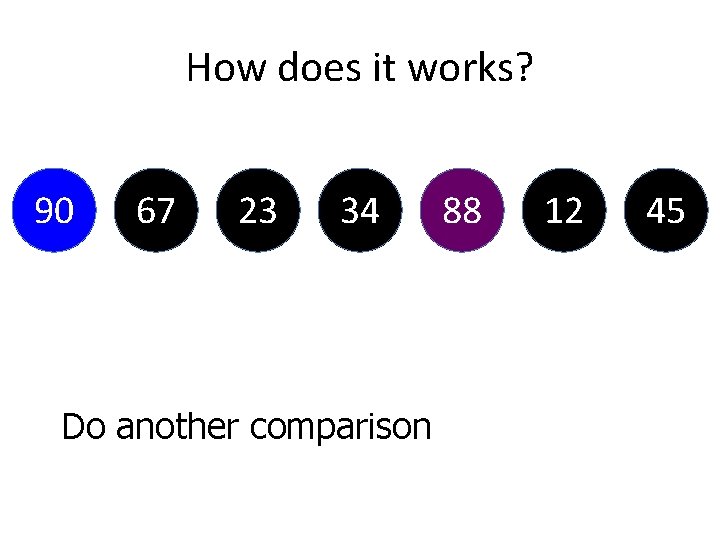
How does it works? 90 67 23 34 Do another comparison 88 12 45
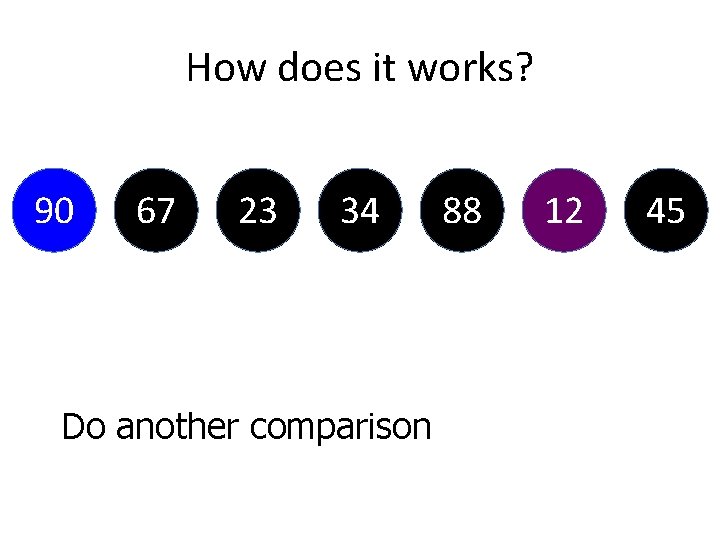
How does it works? 90 67 23 34 Do another comparison 88 12 45
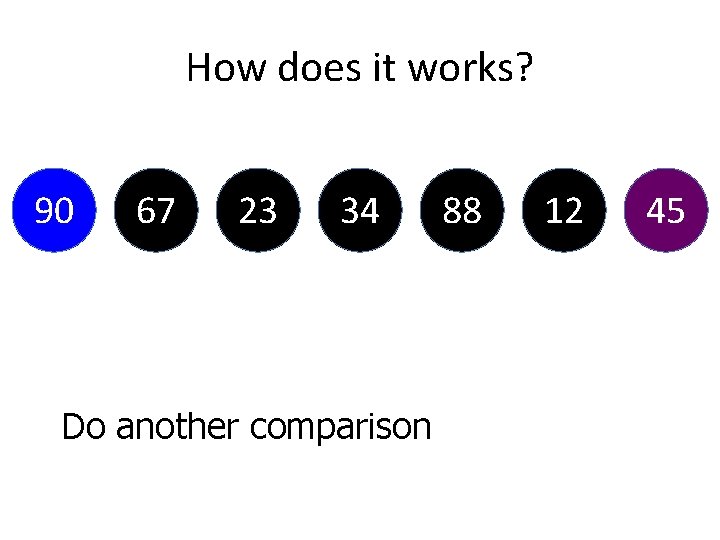
How does it works? 90 67 23 34 Do another comparison 88 12 45

After several pass Default 34 67 23 90 88 12 45 1 st Pass 90 67 23 34 88 12 45 2 nd Pass 90 88 23 34 67 12 45 3 rd Pass 90 88 67 34 23 12 45 4 th Pass 90 88 67 45 23 12 34 5 th Pass 90 88 67 45 34 12 23 6 th Pass 90 88 67 45 34 23 12 Done

Example 1 Selection sort for descending order Begin: 84 69 76 86 94 91 Pass 1: 94 69 76 86 84 91 Pass 2: 94 91 76 86 84 69 Pass 3: 94 91 86 76 84 69 Pass 4: 94 91 86 84 76 69 Pass 5: 94 91 86 84 76 69 (done) • While being an easy sort to program, the selection sort is one of the least efficient. The algorithm offers no way to end the sort early, even if it begins with an already sorted list.

Selection sort • Selection sort is a simple, but inefficient, sorting algorithm. • The selection sort is a combination of searching and sorting. • During each pass, the unsorted element with the smallest (or largest) value is moved to its proper position in the array. • The number of times the sort passes through the array is one less than the number of items in the array. In the selection sort, the inner loop finds the next smallest (or largest) value and the outer loop places that value into its proper location.

Selection sort • The selection sort works by selecting the smallest unsorted item remaining in the list, and then swapping it with the item in the next position to be filled. The selection sort has a complexity of O(n 2). – Pros: Simple and easy to implement. – Cons: Inefficient for large lists, so similar to the more efficient insertion sort that the insertion sort should be used in its place.

Selection sort (continue) It yields a 60% performance improvement over the bubble sort, but the insertion sort is over twice as fast as the bubble sort and is just as easy to implement as the selection sort. In short, there really isn't any reason to use the selection sort - use the insertion sort instead.

For selection sort in general • The number of comparisons when the array contains N elements is Sum = (N-1) + (N-2) +. . . + 2 + 1 Sum = N * (N-1) /2 Sum =. 5 N 2 -. 5 N Sum = O(N 2)

Number of Comparisons

How to code • Selection sort involves: – Finding the smallest/largest element – Swapping process – Check with all element – Iterate until reach end of array list So, you need to have some sort of “if-else” and “for looping”

First Step of Develop Selection Sort in C++ Code • It must have swapping process. So, how do you swap stuff? • But let us first declare some array and get input and display the input before sorting • We will perform descending order of sorting


First Step of Develop Selection Sort C++ Code • At First, we will find the largest value of elements inside the array list and keep it into temporary variable • Then, we update our index location of the largest value

First Step of Develop Selection Sort C++ Code

First Step of Develop Selection Sort C++ Code Output

Second Step of Develop Selection Sort C++ Code Once we know how to find the largest value in the array list, we need to keep it in descending order position so the largest value will be put in the first position

Second Step of Develop Selection Sort C++ Code

Second Step of Develop Selection Sort C++ Code Modification on original First Step

Second Step of Develop Selection Sort C++ Code Iterate according to the number of elements in an array list Modification on original First Step

Second Step of Develop Selection Sort C++ Code Set large to initial condition of “j” Modification on original First Step

Second Step of Develop Selection Sort C++ Code “FOR” loop has set up initial condition to “int i = j+1” so we would not need to iterate from starting anymore but from “j+1” Modification on original First Step

Second Step of Develop Selection Sort C++ Code If the current “i” has bigger value of element than the “large” element. Set large to “i” value. Modification on original First Step

Second Step of Develop Selection Sort C++ Code As usual, switch place with the biggest value according to current “j” position Modification on original First Step
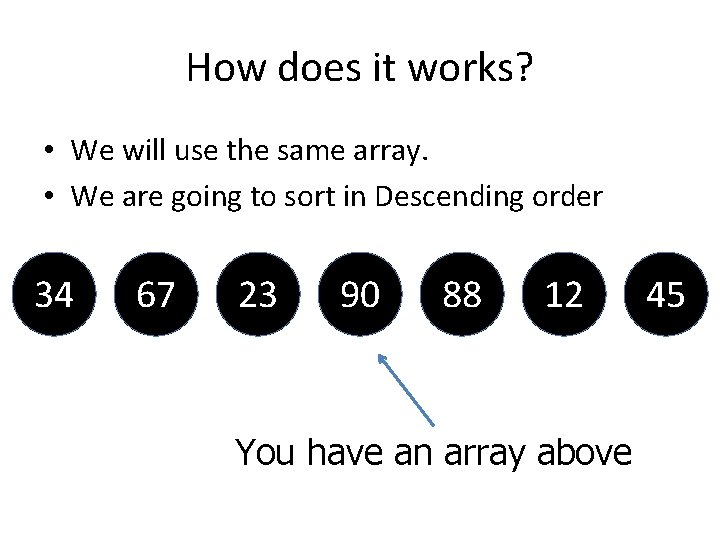
![Algorithm for Selection Sort Coding fora0 asize a smallesta forba1 bsize b ifdatabdatasmallest Algorithm for Selection Sort Coding for(a=0; a<size; a++) { smallest=a; for(b=a+1; b<size; b++) if(data[b]<data[smallest])](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-75.jpg)
Algorithm for Selection Sort Coding for(a=0; a<size; a++) { smallest=a; for(b=a+1; b<size; b++) if(data[b]<data[smallest]) smallest=b; temp=data[a]; data[a]=data[smallest]; data[smallest]=temp; } Algorithm: array A with n elements 1. Find the smallest of A[1], A[2]…A[n] and swap the number in position A[1]. 2. Find the next smallest value and swap in the 2 nd position A[2]. (A[1]≤A[2]). 3. Continue process until A[n-1]≤A[n].
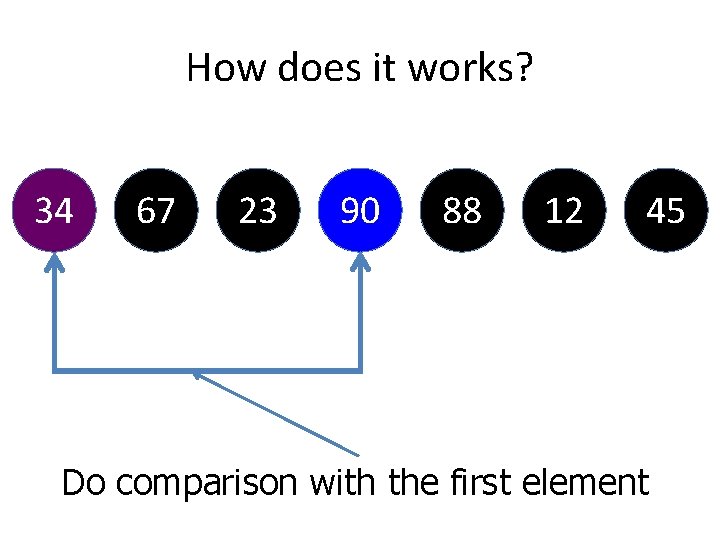
![Another Style of Coding void selectionint array int size int select int i Another Style of Coding void selection(int array[], int size, int select) { int i,](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-76.jpg)
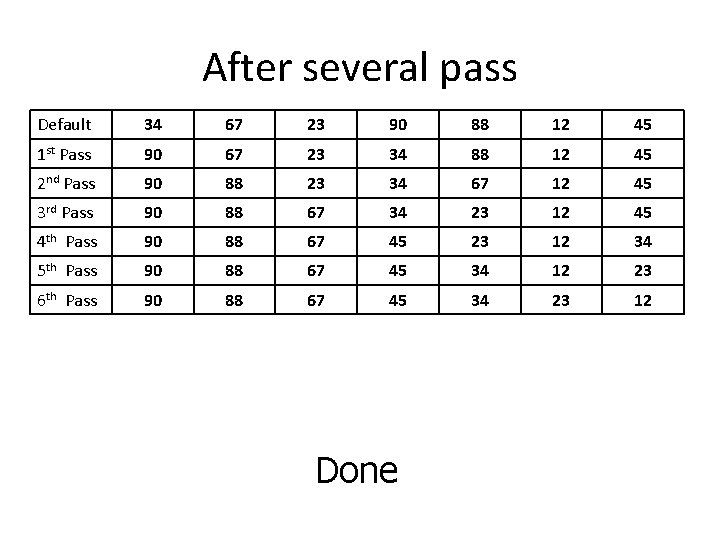
Another Style of Coding void selection(int array[], int size, int select) { int i, j, min, temp; for(i=0; i<size-1; i++) { min i; for(j=i+1; j<size; j++) { if((array[j]<array[j-1])&&(select==1))//ascending min=j; else if((array[j]>array[j 1])&&(select==2))//descending min=j; } temp=array[min]; array[min]=array[i]; array[i]=temp; } } }

INSERTION SORT IMPLEMENTATION

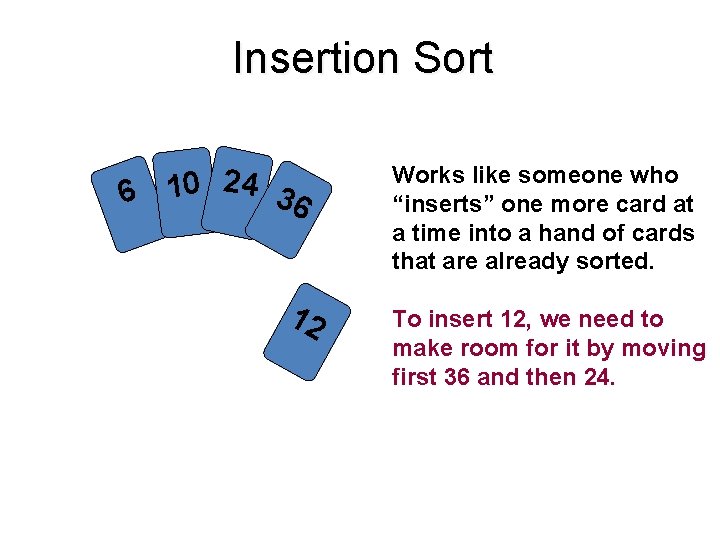
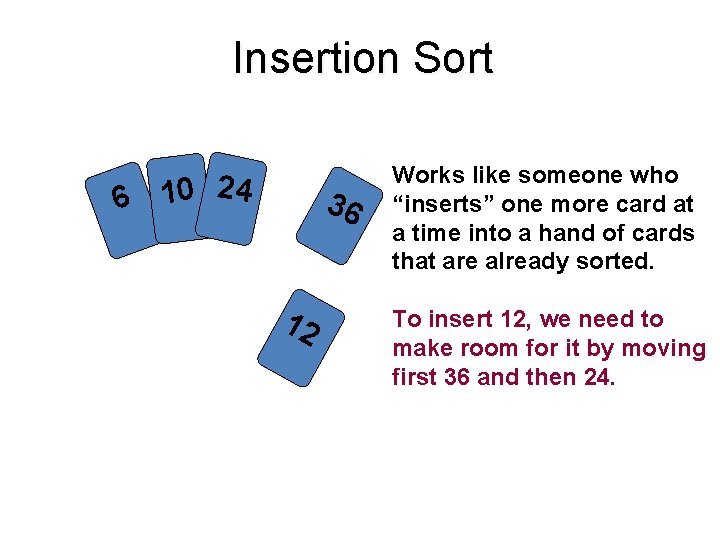
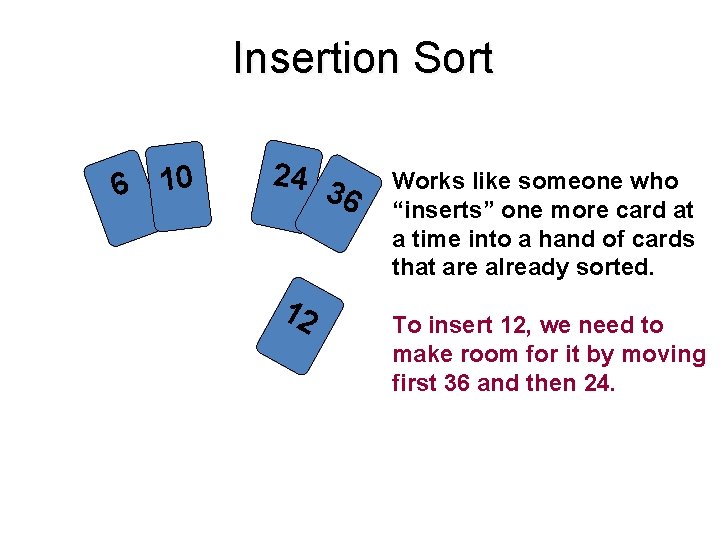
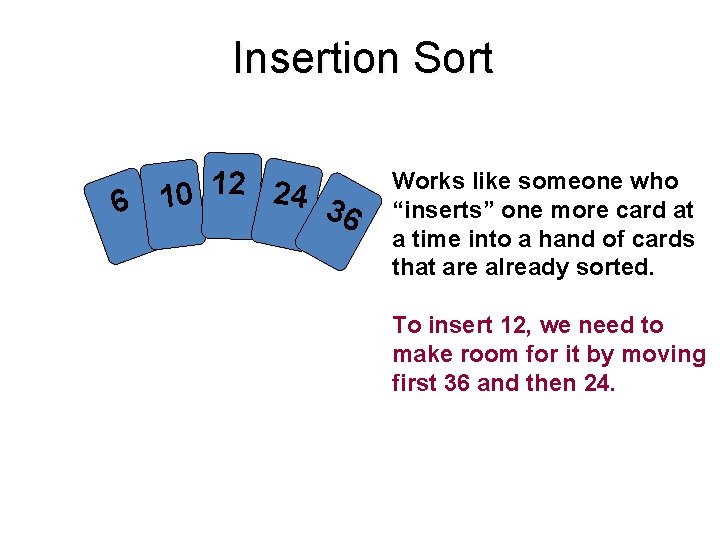
Insertion sort • The insertion sort, unlike the other sorts, passes through the array only once. The insertion sort works much in the same way you organize a hand of cards. You pick up the unsorted cards one at a time. As you pick up each card, you insert it into its correct position in your hand of organized cards. • The insertion sort splits an array into two sub-arrays. The first sub-array is always sorted and gets larger as the sort continues. The second sub-array is unsorted and contains all the elements not yet inserted into the first sub-array. The second sub-array gets smaller as the sort progresses.

Insertion Sort 6 10 24 3 6 12 Works like someone who “inserts” one more card at a time into a hand of cards that are already sorted. To insert 12, we need to make room for it by moving first 36 and then 24.

Insertion Sort 6 10 24 36 12 Works like someone who “inserts” one more card at a time into a hand of cards that are already sorted. To insert 12, we need to make room for it by moving first 36 and then 24.

Insertion Sort 6 10 24 3 6 12 Works like someone who “inserts” one more card at a time into a hand of cards that are already sorted. To insert 12, we need to make room for it by moving first 36 and then 24.

Insertion Sort 12 24 0 1 6 36 Works like someone who “inserts” one more card at a time into a hand of cards that are already sorted. To insert 12, we need to make room for it by moving first 36 and then 24.

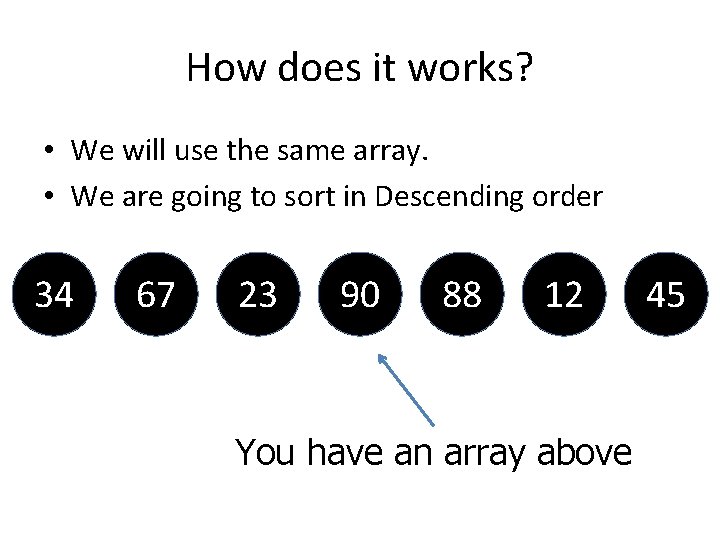
How does it works? • We will use the same array. • We are going to sort in Descending order 34 67 23 90 88 12 You have an array above 45

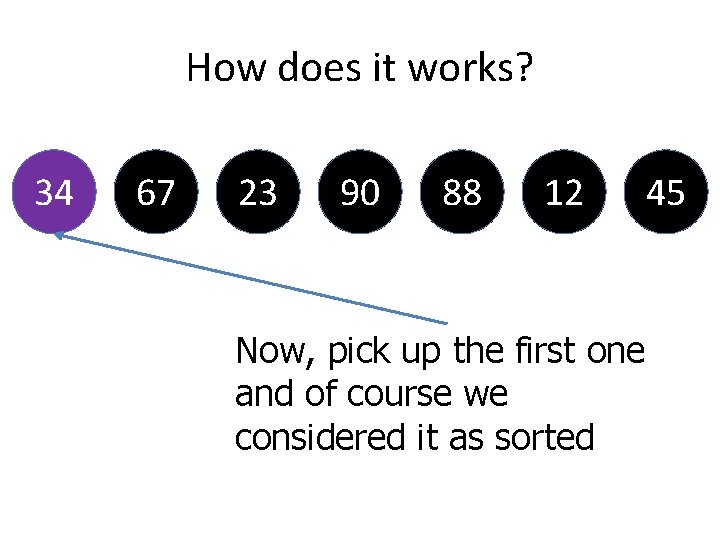
How does it works? 34 67 23 90 88 12 Now, pick up the first one and of course we considered it as sorted 45

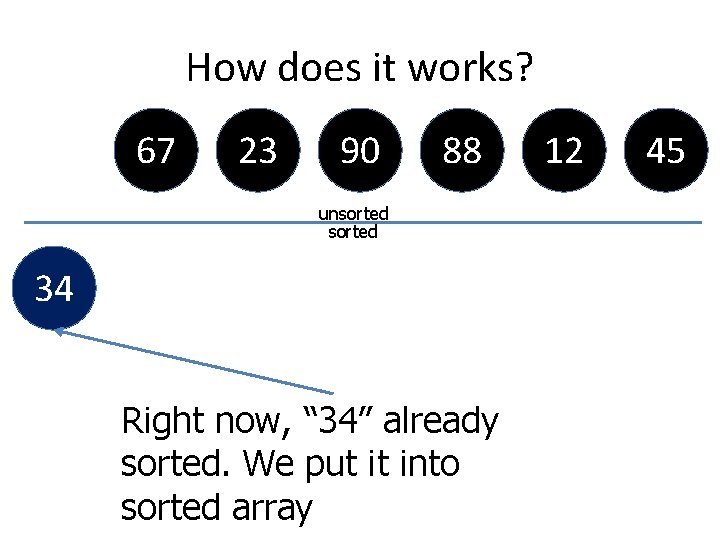
How does it works? 67 23 90 88 unsorted 34 Right now, “ 34” already sorted. We put it into sorted array 12 45

How does it works? 67 23 90 88 12 45 unsorted 34 Now, back at unsorted array, choose “ 67” and since we are going to put it into sorted array, we do comparison whether it is bigger than “ 34” or smaller than “ 34”

How does it works? 23 90 88 12 45 unsorted 67 34 It is bigger than “ 34”, so we put it at the front of “ 34”

How does it works? 23 90 88 12 45 unsorted 67 34 Next, we do comparison between “ 23” with “ 34” and “ 67” whether it is smaller or bigger

After several pass Default 34 67 23 90 88 12 45 1 st Pass 34 67 23 90 88 12 45 2 nd Pass 67 34 23 90 88 12 45 3 rd Pass 67 34 23 90 88 12 45 4 th Pass 90 67 34 23 88 12 45 5 th Pass 90 88 67 34 23 12 45 6 th Pass 90 88 67 34 23 12 45 7 th Pass 90 88 67 45 34 23 12 Done

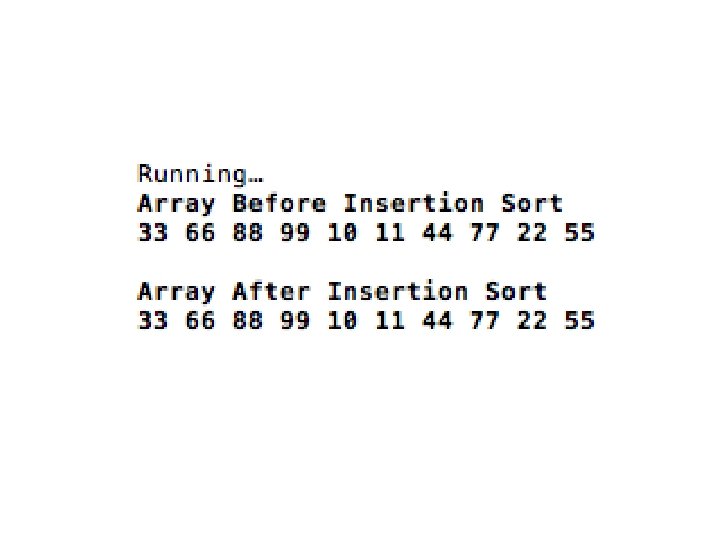
First Step of Develop Insertion Sort in C++ Code • It must have swapping process. So, how do you swap stuff? • But let us first declare some array and get input and display the input before sorting • We will perform descending order of sorting



Step of Develop Insertion Sort C++ Code Declare Temp and Previously variable

Step of Develop Insertion Sort C++ Code Declare a for-loop

Step of Develop Insertion Sort C++ Code Set up the initial condition for each iteration since we do comparison

Step of Develop Insertion Sort C++ Code Now for while loop. Let say the current i = 5, so previously = 4

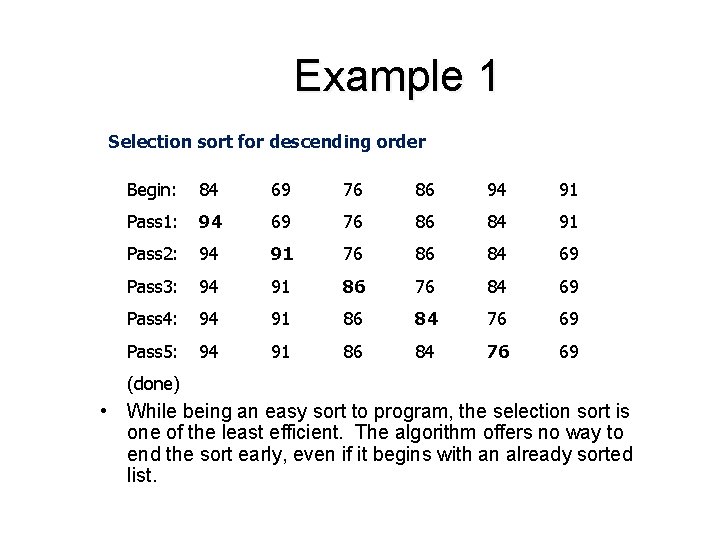
Step of Develop Insertion Sort C++ Code If temp bigger than previously and previously still equal or larger than 0, thus we update the arraylist with the previously value (arrlist[previously+1] get the arrlist[previously]

Step of Develop Insertion Sort C++ Code Then, we loop again since previously will be previously – so, before this previously = 4, now previously = 3. Loop until previously is -1 then we stop
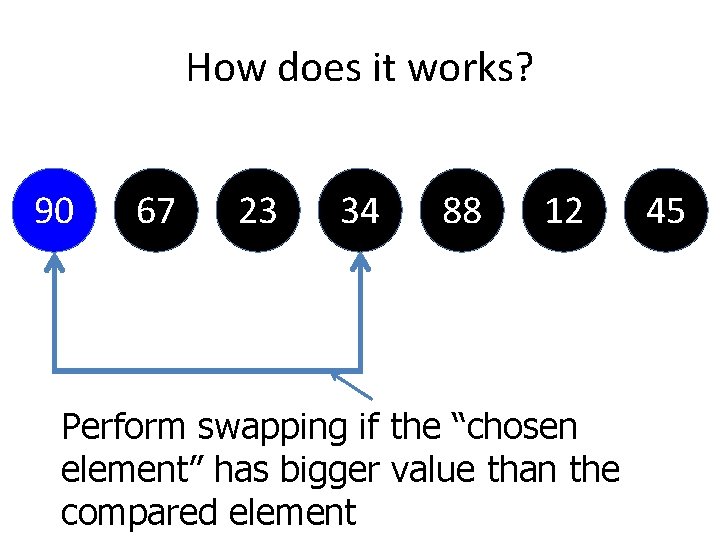
![Step of Develop Insertion Sort C Code If temp is smaller than arrlistpreviously then Step of Develop Insertion Sort C++ Code If temp is smaller than arrlist[previously], then](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-99.jpg)
Step of Develop Insertion Sort C++ Code If temp is smaller than arrlist[previously], then we stop. Put into arrlist[previously+1] the temporary value.

Example 1 • Let's look at our same example using the insertion sort for descending order. • The insertion sort algorithm maintains the two sub-arrays within the same array. When the sort first begins, the first element in the array is considered to be the "sorted array". With each iteration of the loop, the next value in the unsorted section is placed into its proper position in the sorted section. • The insertion sort can be very fast and efficient when used with smaller arrays. Unfortunately, it loses this efficiency when dealing with large amounts of data. • insertion sort is over twice as fast as the bubble sort and almost 40% faster than the selection sort.

Example Descending order • insertion sort is over twice as fast as the bubble sort and almost 40% faster than the selection sort.
![Coding void insertionint array int size int select int i j temp fori1 Coding void insertion(int array[], int size, int select) { int i, j, temp; for(i=1;](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-102.jpg)
Coding void insertion(int array[], int size, int select) { int i, j, temp; for(i=1; i<size; i++) { temp=array[i]; j=i-1; if(select==1) {while(array[j]>temp) { array[j+1]=array[j]; j--; } } else if(select==2) {while((array[j]<temp)&&(j>=0)) { array[j+1]=array[j]; j--; } } array[j+1]=temp; } }

QUICKSORT IMPLEMENTATION

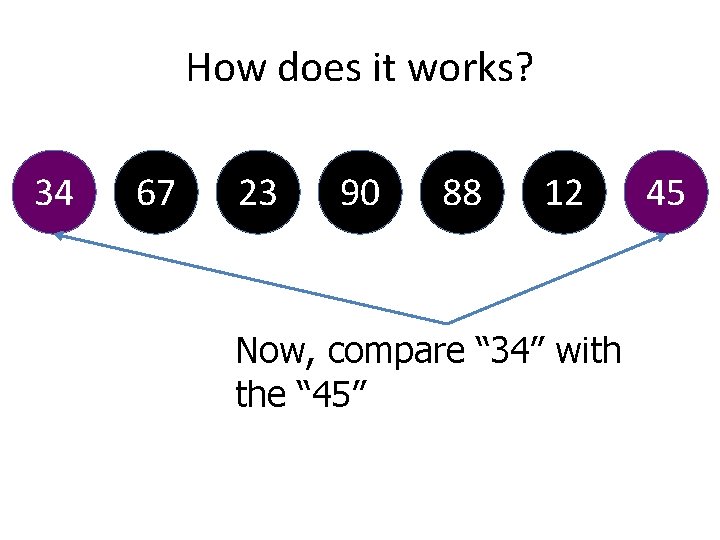
How does it works? • We will use the same array. • We are going to sort in Descending order 34 67 23 90 88 12 You have an array above 45

How does it works? 34 67 23 90 88 12 45 Choose a pivot. Let say “ 34”

How does it works? 34 67 23 90 88 12 45 Choose a pivot. Let say “ 34”

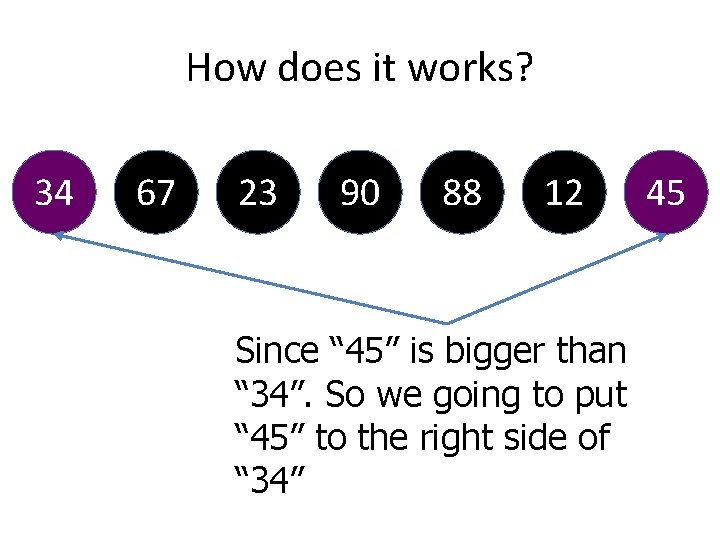
How does it works? 34 67 23 90 88 12 Now, compare “ 34” with the “ 45” 45

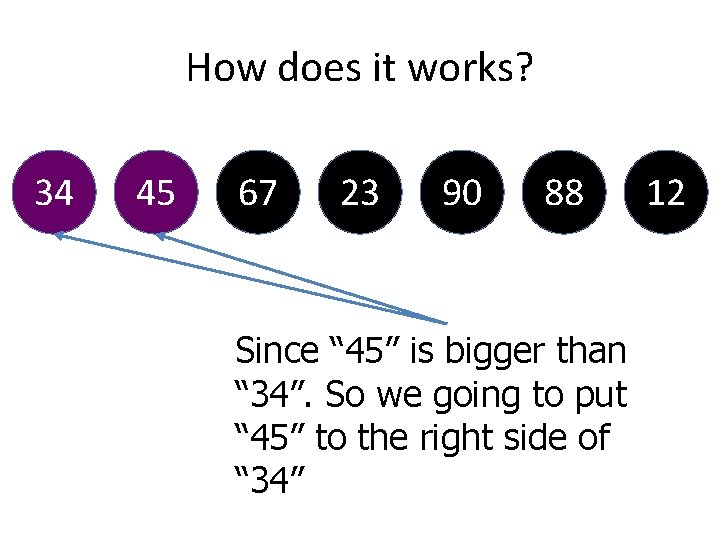
How does it works? 34 67 23 90 88 12 Since “ 45” is bigger than “ 34”. So we going to put “ 45” to the right side of “ 34” 45

How does it works? 34 45 67 23 90 88 Since “ 45” is bigger than “ 34”. So we going to put “ 45” to the right side of “ 34” 12

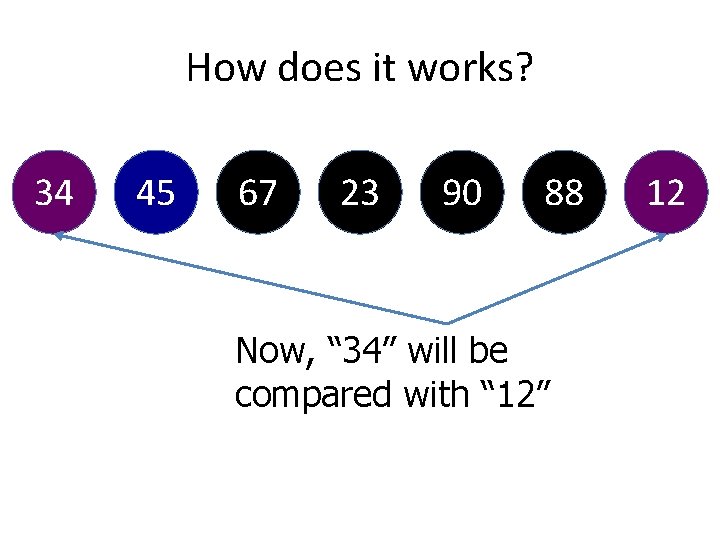
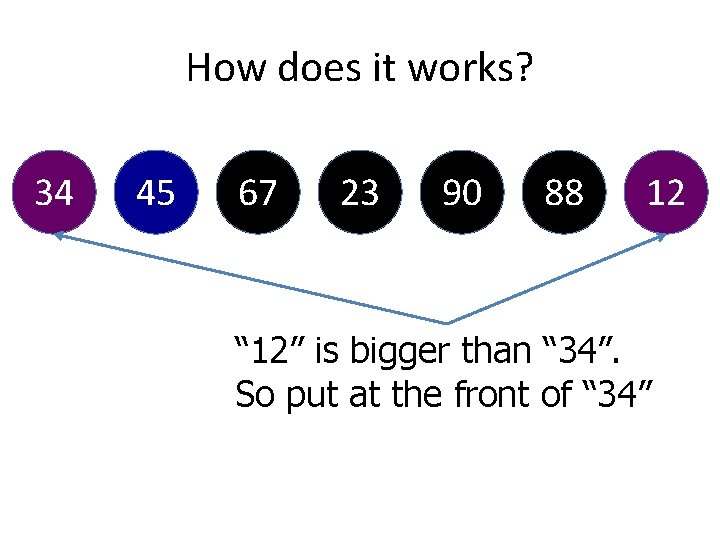
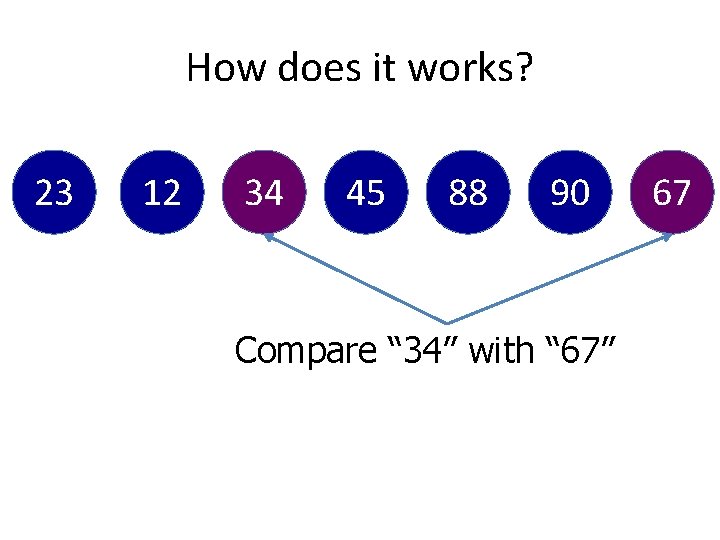
How does it works? 34 45 67 23 90 88 Now, “ 34” will be compared with “ 12” 12

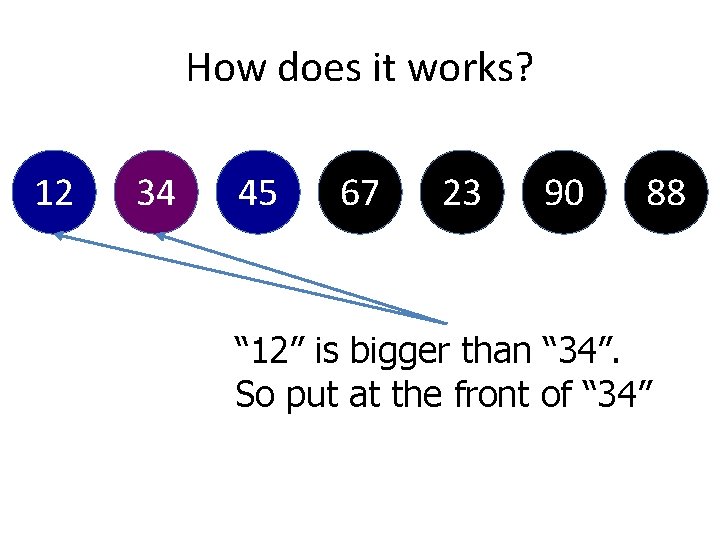
How does it works? 34 45 67 23 90 88 12 “ 12” is bigger than “ 34”. So put at the front of “ 34”

How does it works? 12 34 45 67 23 90 88 “ 12” is bigger than “ 34”. So put at the front of “ 34”

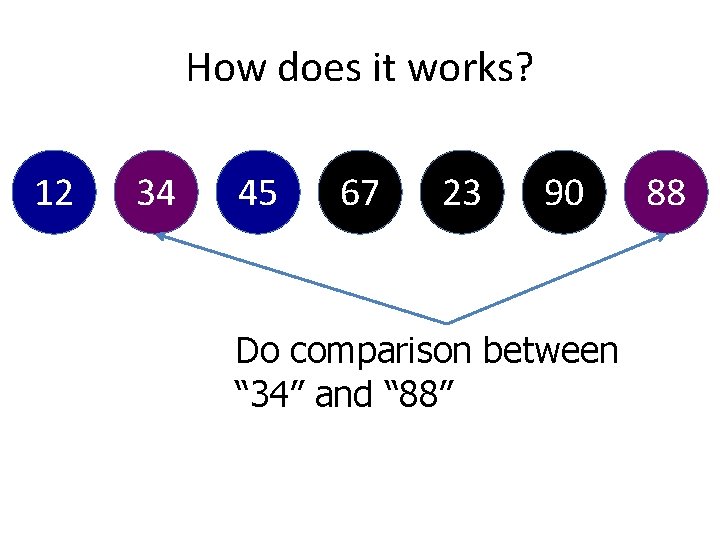
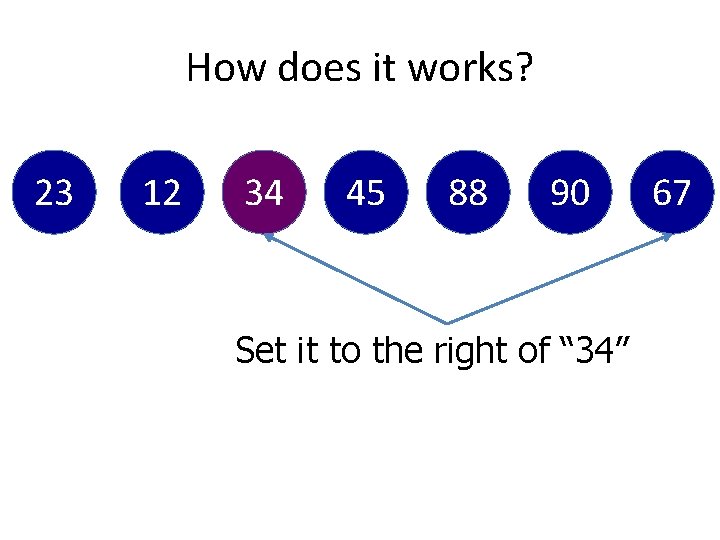
How does it works? 12 34 45 67 23 90 Do comparison between “ 34” and “ 88” 88

How does it works? 12 34 45 88 67 23 Set to the right of “ 34” 90

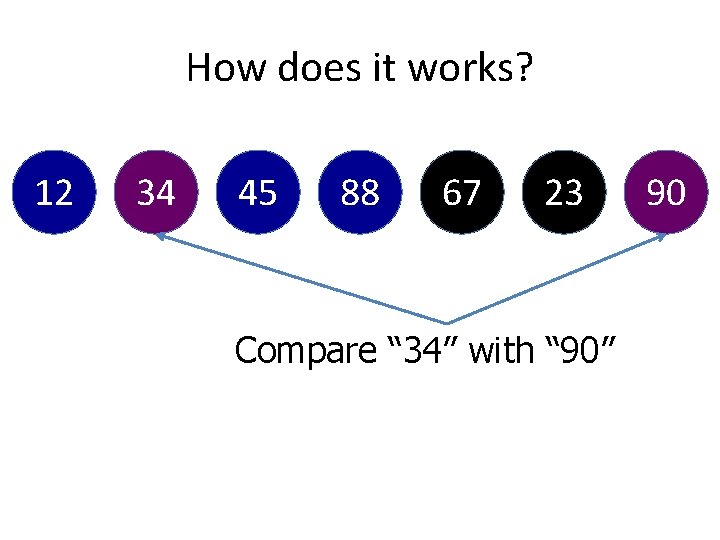
How does it works? 12 34 45 88 67 23 Compare “ 34” with “ 90” 90

How does it works? 12 34 45 88 90 67 Add to the right of “ 34” 23

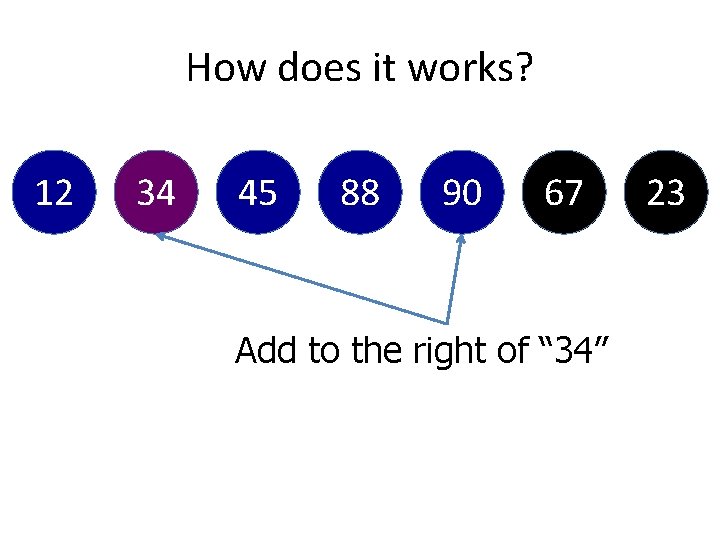
How does it works? 12 34 45 88 90 67 Compare “ 34” with “ 23” 23

How does it works? 23 12 34 45 88 90 Add to the left of “ 34” 67

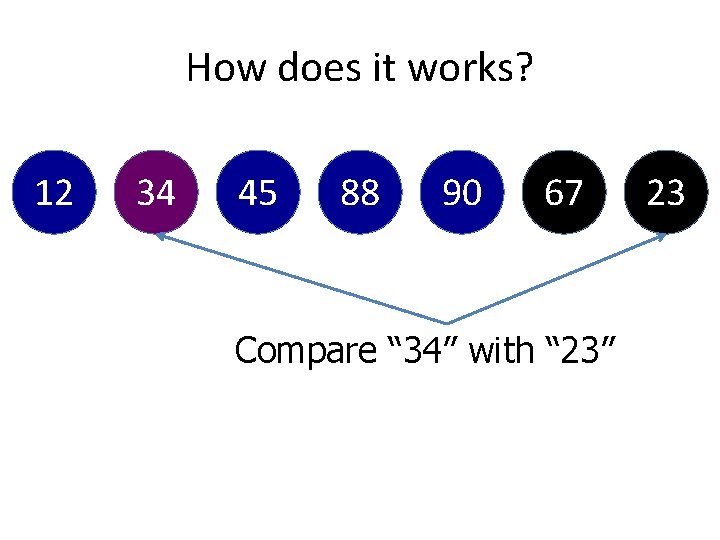
How does it works? 23 12 34 45 88 90 Compare “ 34” with “ 67” 67

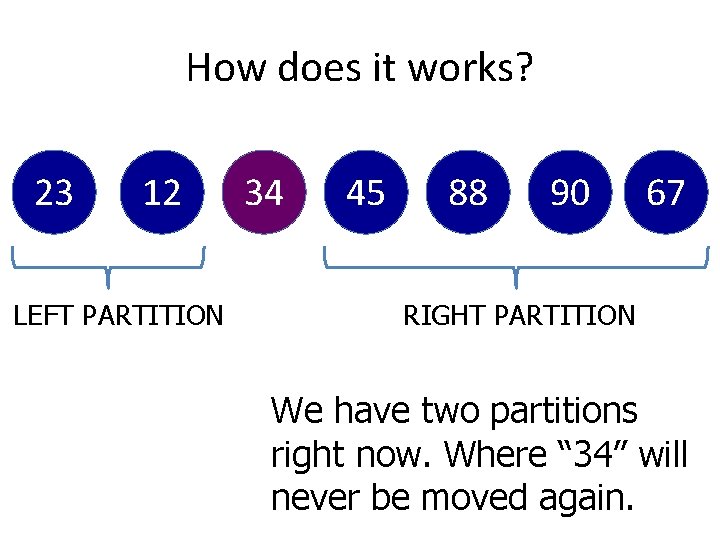
How does it works? 23 12 34 45 88 90 Set it to the right of “ 34” 67

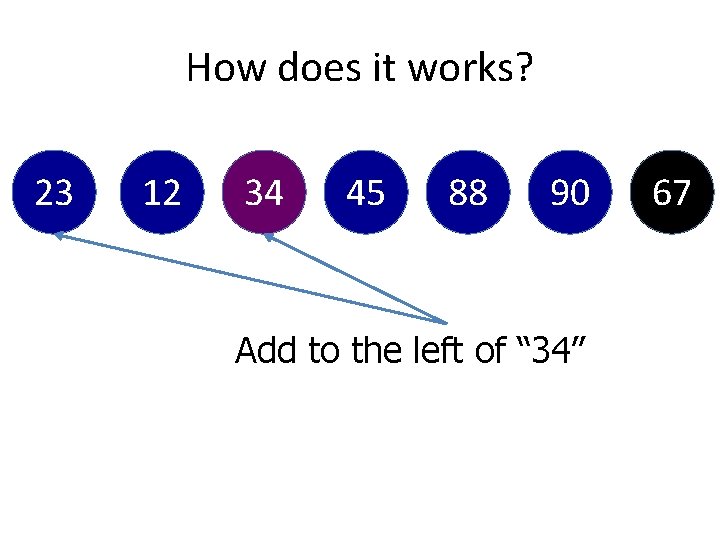
How does it works? 23 12 LEFT PARTITION 34 45 88 90 67 RIGHT PARTITION We have two partitions right now. Where “ 34” will never be moved again.

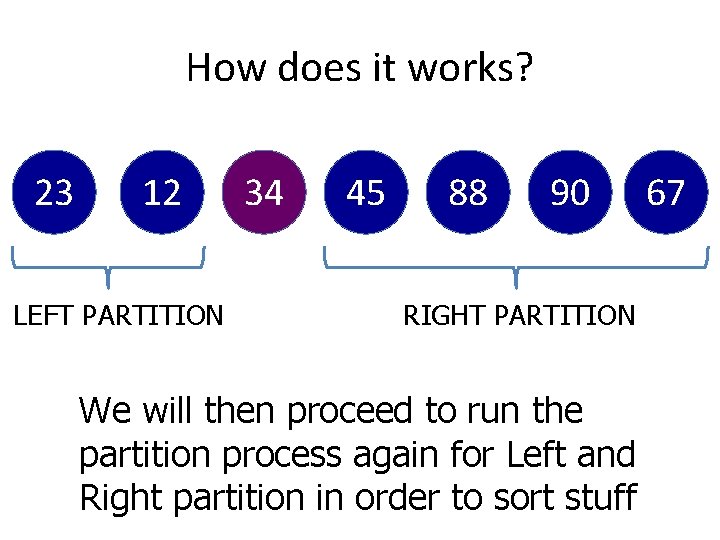
How does it works? 23 12 LEFT PARTITION 34 45 88 90 RIGHT PARTITION We will then proceed to run the partition process again for Left and Right partition in order to sort stuff 67

Quicksort The quicksort is considered to be very efficient, with its "divide and conquer" algorithm. This sort starts by dividing the original array into two sections (partitions) based upon the value of the first item in the array.

How to Code • Let us first declare a pivot and establish a quicksort function • We need to have the array, left and right set up

Phase 1 Quicksort Code Explanation At First, I need to have a function of Quicksort. Where Quicksort function need to have an array to be parsed and left and right index

Phase 1 Quicksort Code Explanation Left and Right is needed in order to classify the index of an array into two sections/partitions. So, if we have an array of ={10, 20, 30, 40}, thus Left is equal to 0 and Right is equal to 3. We do not use the value of an array but the index of an array

Phase 1 Quicksort Code Explanation Now, I’m testing out whether left is smaller than right. Why? Because we need to stop once left is equal to right (Left == Right) based on the value of an array

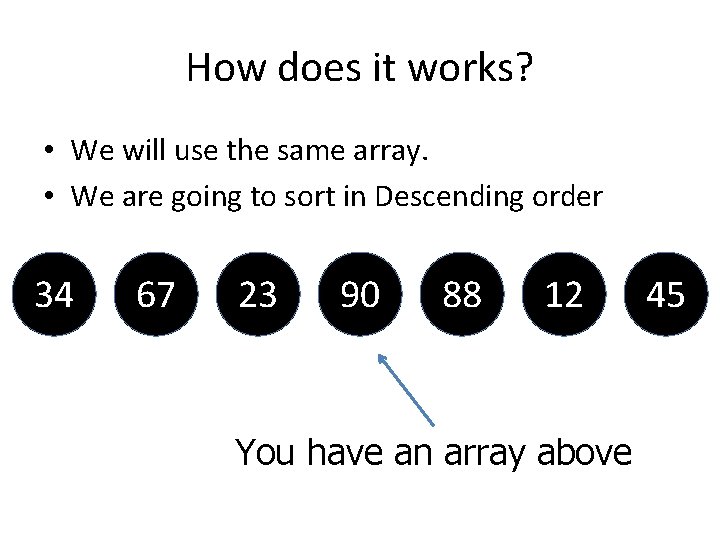
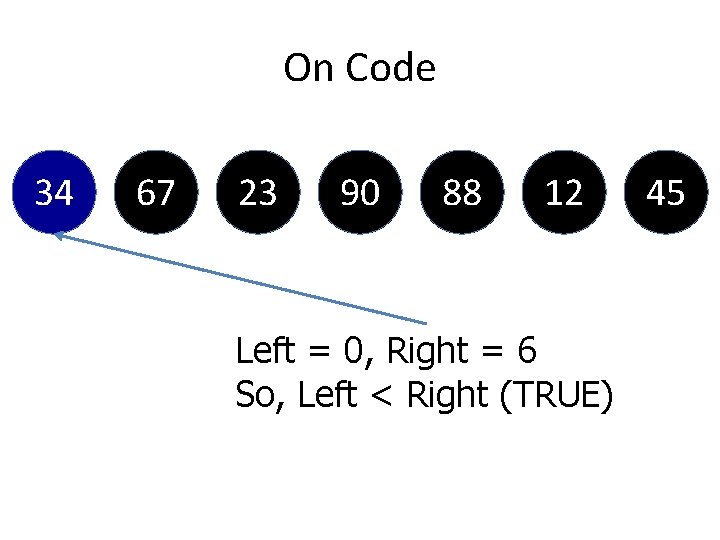
On Code 34 67 23 90 88 12 Left = 0, Right = 6 So, Left < Right (TRUE) 45

Phase 1 Quicksort Code Explanation I’m setting up pivot as the left one. So a[left] is equal to a[0] for the first time we inside this function
![On Code 34 67 23 90 88 aleft a0 34 12 45 On Code 34 67 23 90 88 a[left] @ a[0] = 34 12 45](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-130.jpg)
On Code 34 67 23 90 88 a[left] @ a[0] = 34 12 45

Phase 1 Quicksort Code Explanation Now, I’m going to partition it into two sections/partitions
![Phase 2 Quicksort Code At first aleft which is a0 will be compared with Phase 2 Quicksort Code At first, a[left] which is a[0] will be compared with](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-132.jpg)
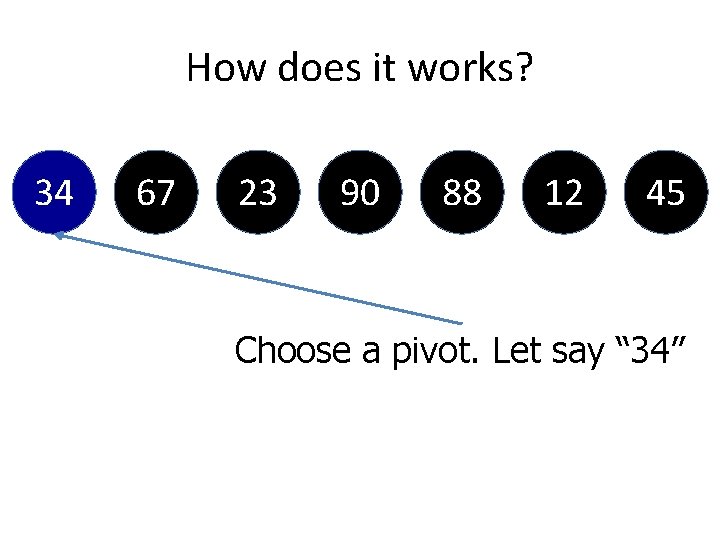
Phase 2 Quicksort Code At first, a[left] which is a[0] will be compared with its own and a[right] also will be compared with a[0] since we are in the first time enter partitioning function

On Code 34 67 Left = 0 23 90 88 12 45 Right = 6
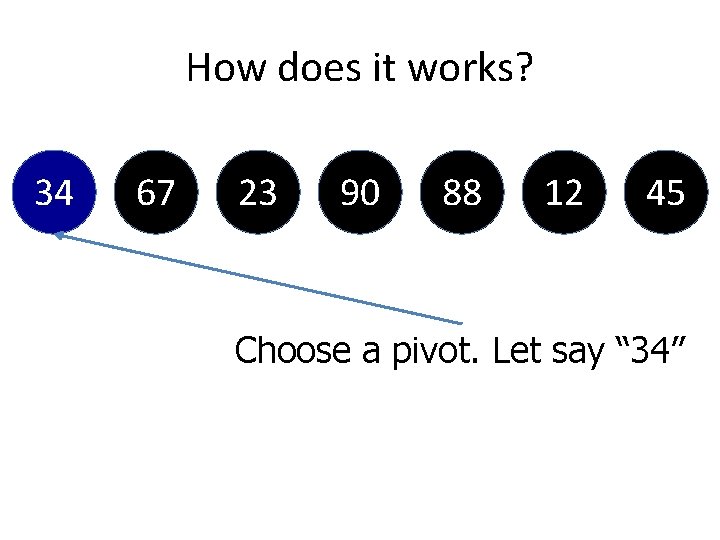
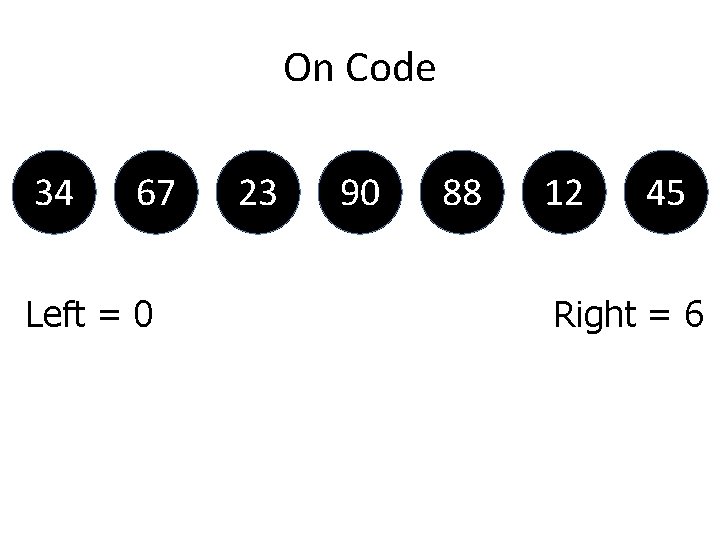
![On Code 34 67 23 90 88 12 while aleft pivot left while On Code 34 67 23 90 88 12 while (a[left] < pivot) left++; while](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-134.jpg)
On Code 34 67 23 90 88 12 while (a[left] < pivot) left++; while (a[right] > pivot) right--; 45
![On Code 34 67 23 90 88 12 while a0 34 left On Code 34 67 23 90 88 12 while (a[0] < 34) left++; -](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-135.jpg)
On Code 34 67 23 90 88 12 while (a[0] < 34) left++; - (Take 34 as a[0]) Which is FALSE, so still LEFT = 0 while (a[6] > 34) right--; - (Take 45 as a[6]) Which is TRUE, so RIGHT = 5 (6 – 1) - [Next (Take 12 as a[5]) ] Which is FALSE, so RIGHT stay equal to 5 45

Phase 2 Quicksort Code We do some TRUE and FALSE test here. Right now, if left is still lower than right AND value on the a[left] is not the same as a[right], we proceed with swapping
![On Code 34 67 23 90 88 12 if left right aleft On Code 34 67 23 90 88 12 if (left < right && a[left]](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-137.jpg)
On Code 34 67 23 90 88 12 if (left < right && a[left] != a[right]) { swapping(a[left], a[right]); } 45
![On Code 34 67 23 90 88 if 0 5 a0 On Code 34 67 23 90 88 if ( 0< 5 && a[0] !=](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-138.jpg)
On Code 34 67 23 90 88 if ( 0< 5 && a[0] != a[5]) { swapping(a[0], a[5]); } 12 45
![On Code 12 67 23 90 88 if 0 5 a0 On Code 12 67 23 90 88 if ( 0< 5 && a[0] !=](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-139.jpg)
On Code 12 67 23 90 88 if ( 0< 5 && a[0] != a[5]) { swapping(a[0], a[5]); } 34 45

Phase 2 Quicksort Code But, do not swap if the “IF” statements is FALSE. Just return right

Phase 2 Quicksort Code So, if we still have left < right. We proceed with this “DO-LOOP”
![Round 2 12 67 23 90 88 34 45 while a0 34 left Round 2 12 67 23 90 88 34 45 while (a[0] < 34) left++;](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-142.jpg)
Round 2 12 67 23 90 88 34 45 while (a[0] < 34) left++; - (Take 12 as a[0]) Which is TRUE, so LEFT = 1 - [Next (Take 67 as a[1]) ] Which is FALSE, so, LEFT stay = 1 while (a[5] > 34) right--; - Which is FALSE, RIGHT = 5 (STOP)
![Round 2 12 34 23 90 88 if 1 5 a1 Round 2 12 34 23 90 88 if ( 1< 5 && a[1] !=](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-143.jpg)
Round 2 12 34 23 90 88 if ( 1< 5 && a[1] != a[5]) { swapping(a[1], a[5]); } 67 45
![Round 3 12 34 23 90 88 67 while a1 34 left Round 3 12 34 23 90 88 67 while (a[1] < 34) left++; -](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-144.jpg)
Round 3 12 34 23 90 88 67 while (a[1] < 34) left++; - (Take 34 as a[1]) Which is FALSE, so LEFT = 1 while (a[5] > 34) right--; - (Take 67 as a[5]) Which is TRUE, so, RIGHT = 4 - Next (Take 88 as a[4]) Which is TRUE, so, RIGHT = 3 - Next (Take 90 as a[3]) Which is TRUE, so, RIGHT = 2 - Next (Take 23 as a[2]) Which is FALSE, so, RIGHT = 2 45
![Round 3 12 23 34 90 88 if 1 2 a1 Round 3 12 23 34 90 88 if ( 1< 2 && a[1] !=](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-145.jpg)
Round 3 12 23 34 90 88 if ( 1< 2 && a[1] != a[2]) { swapping(a[1], a[2]); } 67 45
![Round 4 12 23 34 90 88 67 while a1 34 left Round 4 12 23 34 90 88 67 while (a[1] < 34) left++; -](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-146.jpg)
Round 4 12 23 34 90 88 67 while (a[1] < 34) left++; - (Take 23 as a[1]) Which is TRUE, so LEFT = 2 - Next (Take 34 as a[2]) Which is FALSE, so, LEFT = 2 while (a[2] > 34) right--; - (Take 34 as a[2]) Which is FALSE, so, RIGHT = 2 45

Round 5 12 23 34 90 NO SWAPPING NEEDED JUST RETURN RIGHT = 2 88 67 45

Next Phase • Just continue to quicksort the left and right partition using below code quicksort(a, left, pivot. New - 1); quicksort(a, pivot. New + 1, right); So, there will be smaller partition and it is recursive function

Output (First Part) Array before sorting 34 67 23 90 88 12 45 Right: 5 Swapping 12 67 23 90 88 34 45 Still in Do Left: 1 Swapping 12 34 23 90 88 67 45 Still in Do Right: 4 Right: 3 Right: 2 Swapping 12 23 34 90 88 67 45 Still in Do Left: 2

Output (Second Part) Another Iteration Right: 0 Another Iteration 12 Another Iteration Right: 5 Right: 4 Right: 3 Right: 2 Right: 1 Another Iteration Right: 5 Right: 4 Right: 3 Right: 2

Output (Third Part) Another Iteration Swapping 12 23 34 45 88 67 90 Still in Do Left: 4 Left: 5 Left: 6 Another Iteration Right: 4 Right: 3 Another Iteration Swapping

Output (4 th Part) 12 23 34 45 67 88 90 Still in Do Left: 5 Another Iteration 88 88 Array before sorting 12 23 34 45 67 88 90 Press any key to continue. . .

Coding example (Xcode)

Coding example (XCode)

Visual Studio Code • Refer to the Quicksort. cpp from the folder Contoh. Dalam. Lab

MERGE SORT IMPLEMENTATION

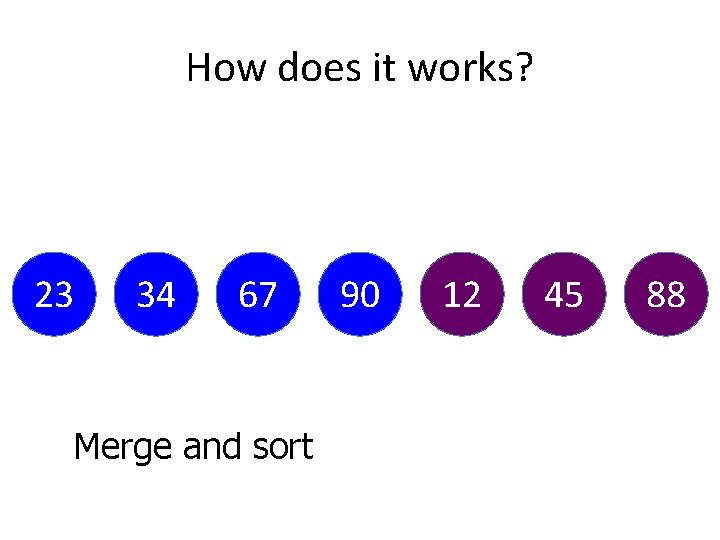
How does it works? • We will use the same array. • We are going to sort in Ascending order 34 67 23 90 88 12 You have an array above 45

How does it works? 34 67 23 90 88 12 45 We are going to divide into two parts

How does it works? 34 67 23 Divide Again 90 88 12 45

How does it works? 34 67 23 90 12 Sort According to group 88 45

How does it works? 23 34 67 Merge and sort 90 12 45 88

How does it works? 12 23 34 45 Merge and sort again 67 88 90

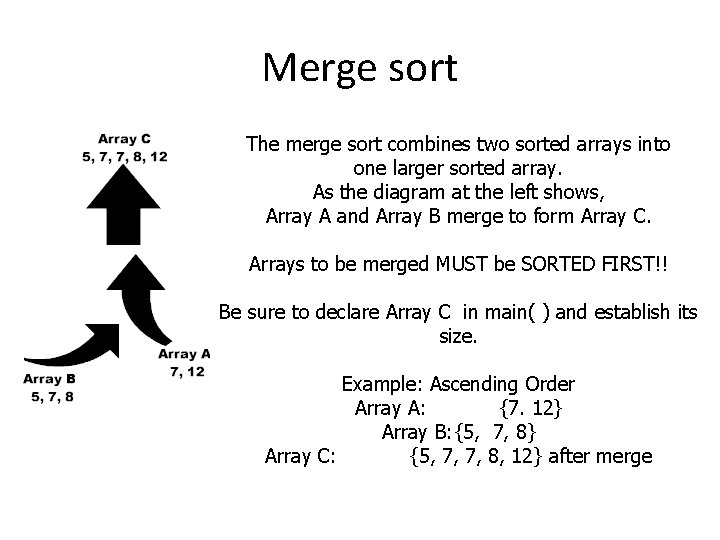
Merge sort The merge sort combines two sorted arrays into one larger sorted array. As the diagram at the left shows, Array A and Array B merge to form Array C. Arrays to be merged MUST be SORTED FIRST!! Be sure to declare Array C in main( ) and establish its size. Example: Ascending Order Array A: {7. 12} Array B: {5, 7, 8} Array C: {5, 7, 7, 8, 12} after merge

Merge sort (continue) Here is how it works: The first element of array A is compared with the first element of array B. If the first element of array A is smaller than the first element of array B, the element from array A is moved to the new array C. The subscript of array A is now increased since the first element is now set and we move on. If the element from array B should be smaller, it is moved to the new array C. The subscript of array B is increased. This process of comparing the elements in the two arrays continues until either array A or array B is empty. When one array is empty, any elements remaining in the other (nonempty) array are "pushed" into the end of array C and the merge is complete.

Merge Sort Algorithm The merge sort algorithm continuously divides a list in half and then sorts them as the halves combined together. To sort a list using merge sort: 1. If the list contains only one element, it is already sorted. 2. If the list contains two elements, these elements are either in the correct order and the list is already sorted, or they are not, so interchange them. 3. Otherwise, divide the list in half, sort each of the two halves, and then merge them.

Example Sorting a list using merge sort: • • Original (Z A C F Q B G K P N D E M H R T) Divide (Z A C F Q B G K)(P N D E M H R T) Divide (Z A C F)(Q B G K)(P N D E)(M H R T) Divide (Z A)(C F)(Q B)(G K)(P N)(D E)(M H)(R T) Sort pairs (A Z)(C F)(B Q)(G K)(N P)(D E)(H M)(R T) Merge (A C F Z)(B G K Q)(D E N P)(H M R T) Merge (A B C F G K Q Z)(D E H M N P R T) Merge (A B C D E F G H K M N P Q R T Z)

How to code Declare an array as usual

Merge sort function In merge sort function, we can include an array to be parsed, lowest array location and highest location • “a” is our declared array • 0 is our lowest array location • num-1 is our highest location

Merge sort function Let us see what each line do

Merge sort function Declare a pivot (some sort of reference point)

Merge sort function Same as Quicksort, we check whether low array index location is low than high array index location

Merge sort function Getting an integer type pivot

Merge sort function Ok, for first time, we use low index with pivot Then, it reclusively run pivot+1 and high index And, we merge the sorted array

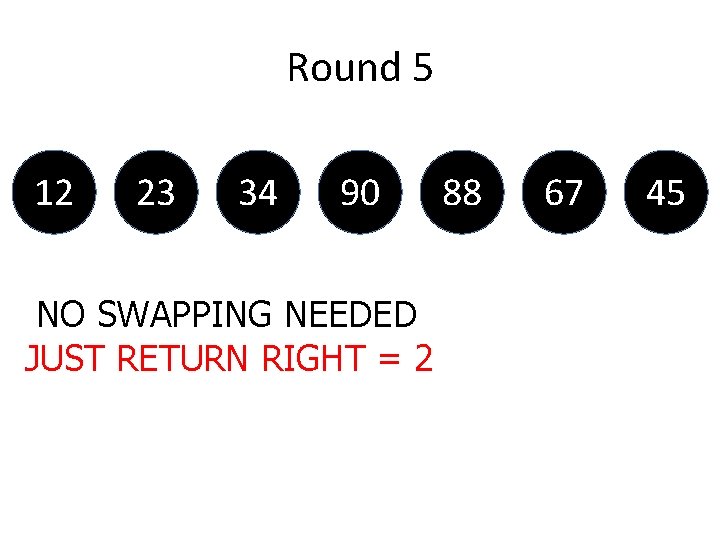
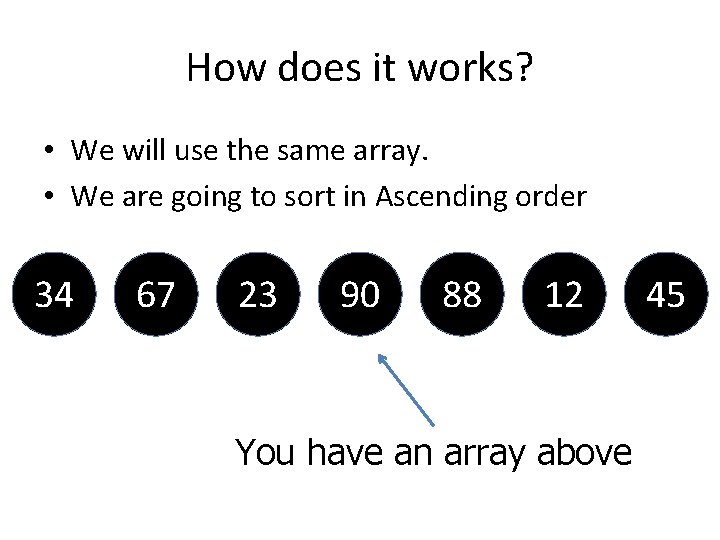
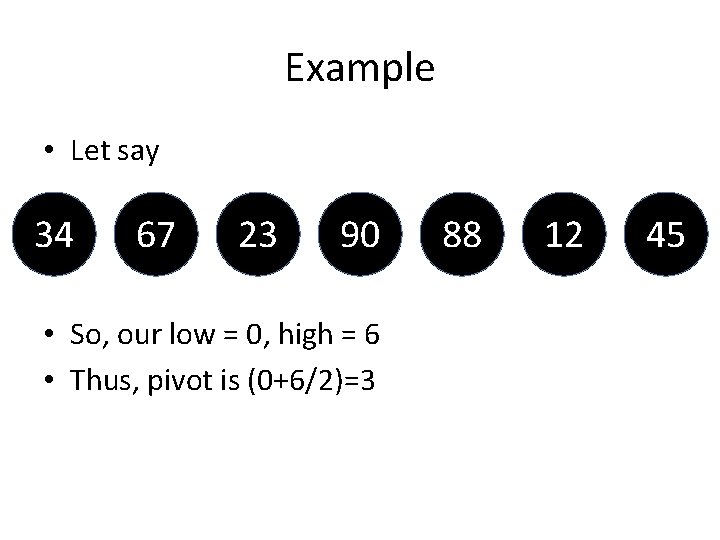
Example • Let say 34 67 23 90 • So, our low = 0, high = 6 • Thus, pivot is (0+6/2)=3 88 12 45
![Example 34 67 23 90 88 12 45 First mergesort is ourarray 0 3 Example 34 67 23 90 88 12 45 First mergesort is ([ourarray], 0, 3)](https://slidetodoc.com/presentation_image_h2/ca42b6cb4da1e3e4dc900631587385d3/image-175.jpg)
Example 34 67 23 90 88 12 45 First mergesort is ([ourarray], 0, 3) -> our first partition/division Second mergesort is ([ourarray], 4, 6) -> our second partition/division merge is ([ourarray], 0, 3, 6) -> our merge function

Merge function Ok, now it is a merge function, we get an indexed array, low index location, pivot that we have calculated, and high index location

Merge function • Declare a two integer that carries low index location (h and i) and one integer (j) to handle pivot+1 • b[high+1] is temporary array to sorting an array before parsed back to original array

Merge function • While statement, we need to make sure that current h (low index location) is lower or equal with pivot AND current j (pivot+1) is lower or equal with high index location

I’m using below example 23 34 67 90 12 45 We parsed our array, low = 0, pivot = 3, high = 6 So, h = 0; i = 0; and j = 4 88

I’m using below example 23 34 67 90 12 45 low = 0, pivot = 3, high = 6; h = 0; i = 0; and j = 4 While ((0<=3) && (4<=6) - > TRUE if (a[0] 23 <= a[4] 12) -> FALSE b[0] = a[4] 12; j++ 5; i++ 1; 88

I’m using below example 23 34 67 90 12 45 low = 0, pivot = 3, high = 6; h = 0; i = 1; and j = 5 While ((0<=3) && (5<=6) - > TRUE if (a[0] 23 <= a[5] 45) -> TRUE b[1] = a[0] 23; h++ 1 ; i++ 2; 88

I’m using below example 23 34 67 90 12 45 low = 0, pivot = 3, high = 6; h = 1; i = 2; and j = 5 While ((1<=3) && (5<=6) - > TRUE if (a[1] 34 <= a[5] 45) -> TRUE b[2] = a[1] 34; h++ 2; i++ 3; 88

I’m using below example 23 34 67 90 12 45 low = 0, pivot = 3, high = 6; h = 2; i = 3; and j = 5 While ((2<=3) && (5<=6) - > TRUE if (a[2] 67 <= a[5] 45) -> FALSE b[3] = a[5] 45; j++ 6; i++ 4; 88

I’m using below example 23 34 67 90 12 45 low = 0, pivot = 3, high = 6; h = 2; i = 4; and j = 6 While ((0<=3) && (6<=6) - > TRUE if (a[2] 67 <= a[6] 88) -> TRUE b[4] = a[2] 67; h++ 3; i++ 5; 88

I’m using below example 23 34 67 90 12 45 low = 0, pivot = 3, high = 6; h = 3; i = 5; and j = 6 While ((0<=3) && (6<=6) - > TRUE if (a[3] 67 <= a[6] 88) -> TRUE b[4] = a[2] 67; h++ 3; i++ 5; 88

I’m using below example 23 34 67 90 12 45 low = 0, pivot = 3, high = 6; h = 0; i = 3; and j = 7 While ((0<=3) && (7<=6) - > FALSE 88

I’m using below example 23 34 67 90 12 45 low = 0, pivot = 3, high = 6; h = 0; i = 3; and j = 7 If (h (0) > pivot (3)) -> FALSE 88

Loop (from previous slide) • • • For loop from k=0 UNTIL K<=3 b [3] = a[0] (90); i++ 4; b[4] = a[1] (67); i++ 5; B[5] = a[2] (34); i++ 6; B[6] = a[3] (23); i++ 7;

I’m using below example 12 23 34 45 67 88 low = 0, pivot = 3, high = 6; h = 0; i = 7; and j = 7 FOR LOOP k=0 UNTIL k<=6 a[0]=b[0] 90

Quick Sort & Merge Sort of N elements: How many comparisons? The entire array can be subdivided into halves only log 2 N times. Each time it is subdivided, function Merge is called to re-combine the halves. Function Merge uses a temporary array to store the merged elements. Merging is O(N) because it compares each element in the subarrays. Copying elements back from the temporary array to the values array is also O(N). MERGE SORT IS O(N*log 2 N).