Linear Sorting Comparison based sorting Any sorting algorithm

Linear Sorting

Comparison based sorting • Any sorting algorithm which is based on comparing the input elements has a lower bound of • Proof, since there are n values in the input there are n! permutations of the values. Each permutation should return the same output in the sorting algorithm. We can simulate the sorting process as a decision tree.

Comparison based sorting • The decision tree has n! leafs • The height of the tree is the number of comparisons that are executed for a given permutation of the sorted values, therefore the height of the tree is the running time algorithm

Comparison based sorting • What is the minimal height for a tree of n! leafs ? • A binary tree of height h can contain no more than leafs.

Is comparison a must ? • Think of the problem of sorting a deck of cards. You would most probably keep a pile for each value from Ace to King, and put all cards with the same value in the same pile. • Next we will sort each pile according to it’s suit, but since there are only 4 cards per pile, this will be done constant time for each pile. • We finished sorting the deck, in linear time.

Linear time sorting • Linear time is the minimal time requires to read a list of values of size n. can linear time be enough for sorting? • We show that if you gain some prior knowledge on the values to be sorted we can sort in linear time

Counting Sort • The assumption: all elements are of a known range [1. . k]. • If k is O(n) the running time is also O(n). • The idea: for each element x determine how many elements are smaller than x. if there are 17 elements smaller than x, clearly x should be placed at the 18 th position then construct a new sorted array based on these values.

Counting Sort • Counting-Sort(A, B, k) for all i, initialize C[i] 0 for j 1 to length[A] do C[A[j]] ++ // now C[j] contains the number of elements equal to j for i 2 to k do C[i] + C[i -1] // now C[j] contains the number of elements // less than or equal to j for j length[A] downto 1 do B[C[A[j]]] A[j] C[A[j]] --

Counting Sort • N = 8, K = 7 (0… 6) A 0 1 1 3 2 2 3 6 4 3 5 5 C 0 1 1 1 2 1 3 2 4 0 5 1 6 2 6 6 7 0 C[j] contains all elements less than or equal to j C[j] contains all elements equal to j 0 1 1 2 2 3 3 5 4 5 5 6 6 8

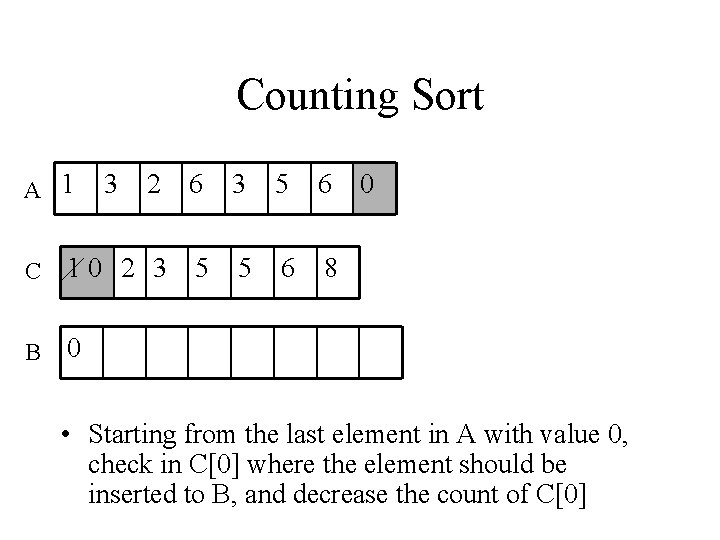
Counting Sort A 1 3 2 6 3 5 6 C 10 2 3 5 5 6 8 B 0 0 • Starting from the last element in A with value 0, check in C[0] where the element should be inserted to B, and decrease the count of C[0]

Counting Sort A 1 3 0 6 3 10 2 3 C B 2 1 2 3 5 6 0 54 5 6 876 3 5 6 6 Since we start from the last index of A results in a stable sort O(n+k) = O(n)

Bucket sort • The assumption. – We assume that all of the n elements are distributed evenly in a known range of values from 1 to m. – We can set up n buckets, each responsible for an interval of m/n numbers from 1 to m. if we can easily match a value to it’s bucket then we will be able to place all the elements in their bucket’s in linear time

Bucket sort • With uniformly distributed keys, the expected number of items per bucket is 1. Thus sorting each bucket takes O(1) time! • The total effort of bucketing, sorting buckets, and concatenating the sorted buckets together is O(n).

Bucket Sort Assuming the elements are uniformly distributed over the interval [0, 1) Bucket. Sort(A) n legnth(A) for i 1 to n do insert A[i] into list B[n. A[i]] for i 0 to n-1 do sort list B[i] with insertion sort concatenate the lists B[0] … B[n-1]

Bucket Sort – Put each element in the correct bucket – Sort each bucket – Concatenate the buckets • Putting each element in its bucket and concatenating the buckets will take linear time. • Sorting each bucket depends on the number of elements mapped to each bucket

Bucket Sort • Let ni be the number of elements in bucket i • The time to sort each bucket is therefore total time to sort all buckets will be and the • The probability for each element to fall into a given bucket is p=1/n, so the expected number of elements in each bucket is a binomial distribution

Bucket Sort • So the expected time for sorting all buckets is linear

Worst Case • If the elements are not uniformly distributed we might spend linear time just putting the elements into a single bucket

Radix Sort • Assumption: all elements are represented by the same number of digits and are of a known range. • Intuition: sort from most significant to least significant problem !! • Solution: sort from least significant to most significant digit using a stable sort each time • Radix-Sort(A, d) for i 1 to d do use a stable sort to sort A on digit i

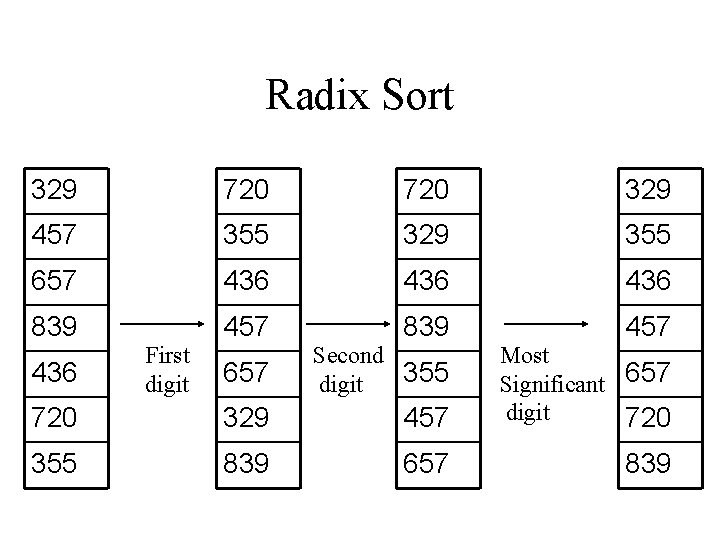
Radix Sort 329 720 329 457 355 329 355 657 436 436 839 457 657 Second 355 digit 720 329 457 Most Significant 657 digit 720 355 839 657 839 436 First digit

Radix Sort • Usually you use Counting Sort for each digit , so we have O(d(k+n)) running time • Proof: by induction on the number of columns • Problem: representing a number in base x requires log(x) digits

Exercise • Can there be a decision tree for input of size n that sorts 1/n of all permutations in time O(n) ? • Or, can there be (n-1)! Leaves at height of O(n)

Exercise • On a binary tree of size n. until height h

Exercise • Given a list of n entries with keys 0 or 1, how can we sort the elements in linear time? • Solution 1: using counting sort k=2 uses O(n) additional memory • If you are allowed to use only O(1) additional memory? • Solution 2: use partition with pivot = 1. Partition will divided the entries to two groups, zeros and ones. • Is partition a stable sort ?

Exercise • What if the entries are strings of d bits, each bit 0 or 1 • Solution: use radix sort can not use partition as it is not stable.