Sorting Algorithms Sorting Sorting is a process that

Sorting Algorithms

Sorting • Sorting is a process that organizes a collection of data into either ascending or descending order. • public interface ISort { void sort(Object[] items, int length); }

Sorting Algorithms • There are many sorting algorithms, such as: – Insertion Sort – Bubble Sort CENG 213 Data Structures

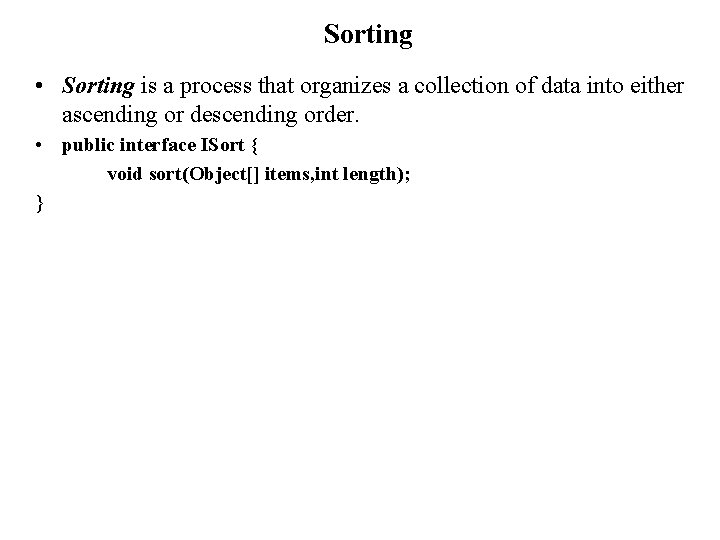
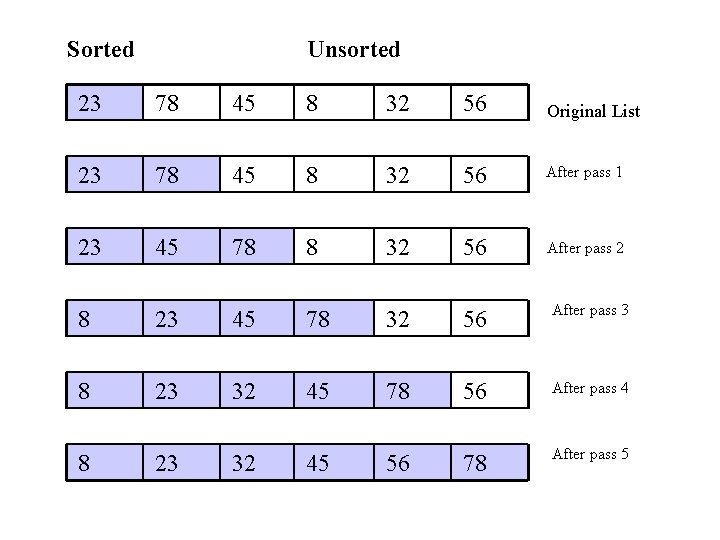
Insertion Sort • Insertion sort is a simple sorting algorithm that is appropriate for small inputs. – Most common sorting technique used by card players. • The list is divided into two parts: sorted and unsorted. • In each pass, the first element of the unsorted part is picked up, transferred to the sorted sublist, and inserted at the appropriate place. • A list of n elements will take at most n-1 passes to sort the data.

Sorted Unsorted 23 78 45 8 32 56 Original List 23 78 45 8 32 56 After pass 1 23 45 78 8 32 56 After pass 2 8 23 45 78 32 56 After pass 3 8 23 32 45 78 56 After pass 4 8 23 32 45 56 78 After pass 5

Insertion Sort Algorithm void insertion. Sort(Object[] a, int n) { for (int i = 1; i < n; i++) { Object tmp = a[i]; for (int j=i; j>0 && tmp < a[j-1]; j--) a[j] = a[j-1]; a[j] = tmp; } }

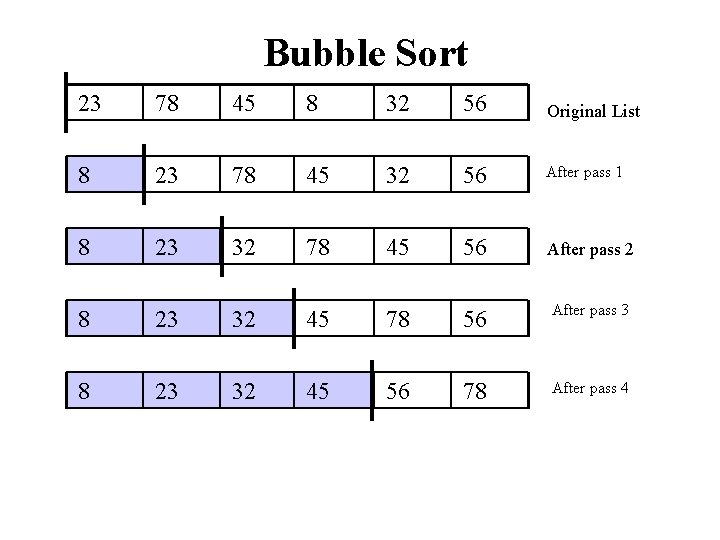
Bubble Sort • The list is divided into two sublists: sorted and unsorted. • The smallest element is bubbled from the unsorted list and moved to the sorted sublist. • After that, the wall moves one element ahead, increasing the number of sorted elements and decreasing the number of unsorted ones. • Each time an element moves from the unsorted part to the sorted part one sort pass is completed. • Given a list of n elements, bubble sort requires up to n-1 passes to sort the data.

Bubble Sort 23 78 45 8 32 56 Original List 8 23 78 45 32 56 After pass 1 8 23 32 78 45 56 After pass 2 8 23 32 45 78 56 After pass 3 8 23 32 45 56 78 After pass 4

Bubble Sort Algorithm void buble. Sort(Object[] a, int n) { bool sorted = false; int last = n-1; for (int i = 0; (i < last) && !sorted; i++){ sorted = true; for (int j=last; j > i; j--) if (a[j-1] > a[j]{ swap(a[j], a[j-1]); sorted = false; // signal exchange } } }

Search public interface ISearch { int search(Object[] search. Space, Object target); }

Linear Search Go through each element and try to find the target. For I from 0 to the n-1 if a[i] == target return i; return -1;

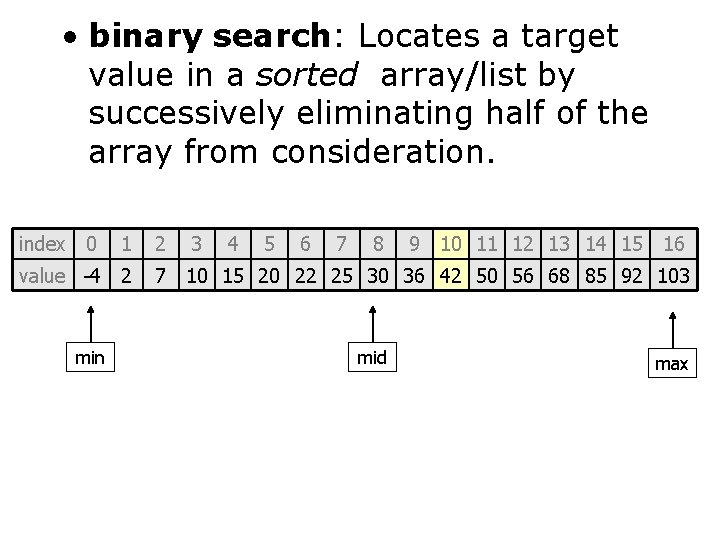
Binary Search • Binary search. Given value and sorted array a[], find index I

• binary search: Locates a target value in a sorted array/list by successively eliminating half of the array from consideration. index 0 1 value -4 2 min 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 7 10 15 20 22 25 30 36 42 50 56 68 85 92 103 mid max

Binary search code // Returns the index of an occurrence of target in a, // or a negative number if the target is not found. // Precondition: elements of a are in sorted order public static int binary. Search(int[] a, int target) { int min = 0; int max = a. length - 1; while (min <= max) { int mid = (min + max) / 2; if (a[mid] < target) { min = mid + 1; } else if (a[mid] > target) { max = mid - 1; } else { return mid; // target found } } } return -(min + 1); // target not found

Recursive binary search (17. 2) • Write a recursive binary. Search method. index 0– If 1 the 2 3 target 4 5 value 6 7 8 is 9 not 10 found, 11 12 13 return 14 15 16 value -4 its 2 7 negative 10 15 20 insertion 22 25 30 36 point. 42 50 56 68 85 92 103 int index = binary. Search(data, 42); // 10 int index 2 = binary. Search(data, 66); // -14