MATH 1330 Vectors Vectors in a plane The












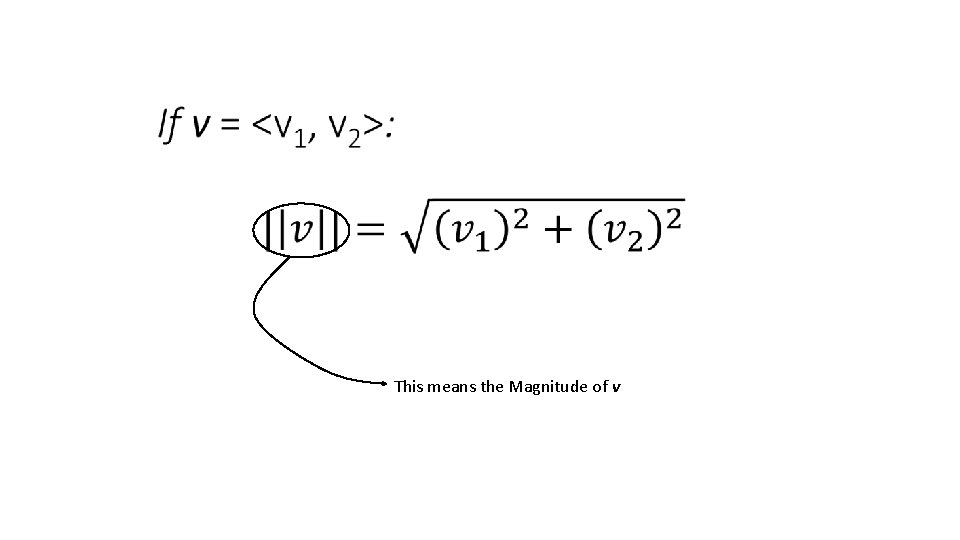




























- Slides: 43

MATH 1330 Vectors

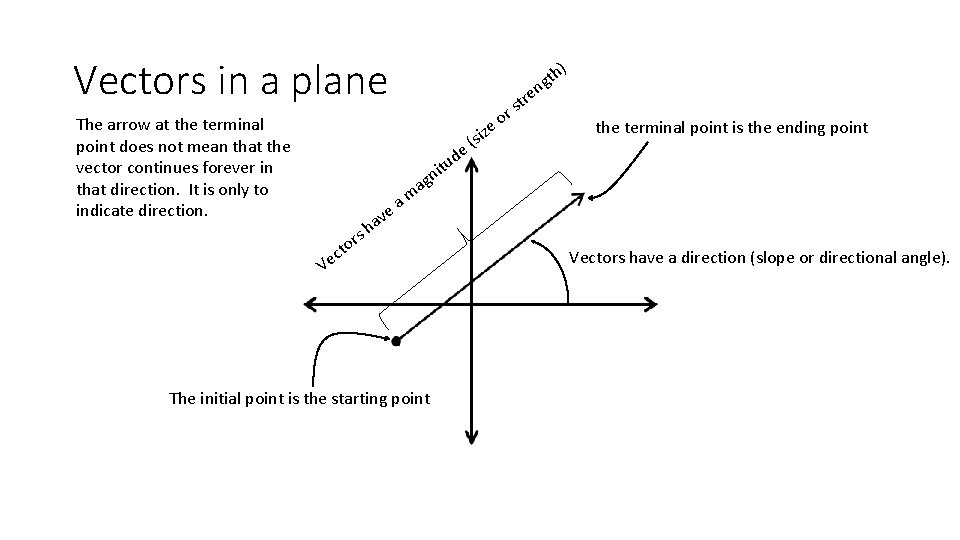
Vectors in a plane The arrow at the terminal point does not mean that the vector continues forever in that direction. It is only to indicate direction. r o e de u it gn z (si en r t s h) t g the terminal point is the ending point a rs cto Ve ve a h am The initial point is the starting point Vectors have a direction (slope or directional angle).

Component Form of a Vector To determine the component form of a vector, v, with initial point P (a, b), and terminal point Q (c, d), you must subtract: terminal point – initial point. v = <c – a, d – b>.

Component Form of a Vector To determine the component form of a vector, v, with initial point P (a, b), and terminal point Q (c, d), you must subtract: terminal point – initial point. v = <c – a, d – b>. This is the vector translated so that the initial point is at (0, 0).

Place the following vectors into component form: u: Initial Point: P (4, -2); Terminal Point (5, 1).

Place the following vectors into component form: u: Initial Point: P (4, -2); Terminal Point (5, 1). u = <5 - 4, 1 - (-2)> = <1, 3>

Place the following vectors into component form: u: Initial Point: P (4, -2); Terminal Point (5, 1). Notice, this is the coordinates of the “new” terminal point u = <5 - 4, 1 - (-2)> = <1, 3>

Place the following vectors into component form: u: Initial Point: P (4, -2); Terminal Point (5, 1). Also, notice that they will both have the magnitude and direction. u = <5 - 4, 1 - (-2)> = <1, 3>

Find the component form of: v: Initial Point: P (0, 4); Terminal Point (9, -3). w: Initial Point: P (-2, 5); Terminal Point (7, 2).

Finding Magnitude and Directional Angle: If you needed to calculate the distance between the terminal and initial points of a vector, what formula can you use?

Finding Magnitude and Directional Angle: •

Finding Magnitude : •

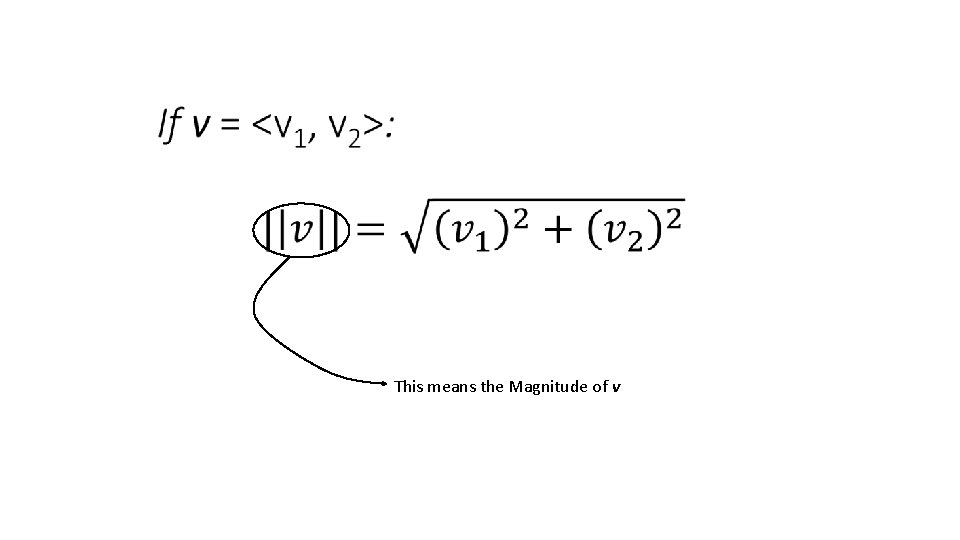
This means the Magnitude of v

Finding Directional Angles If you needed to calculate the angle between the positive x-axis and a vector in standard position, how would you use this?

Finding Directional Angles If you needed to calculate the angle between the positive x-axis and a vector in standard position, how would you use this? How can the unit circle be used here? What trigonometric functions can be used?

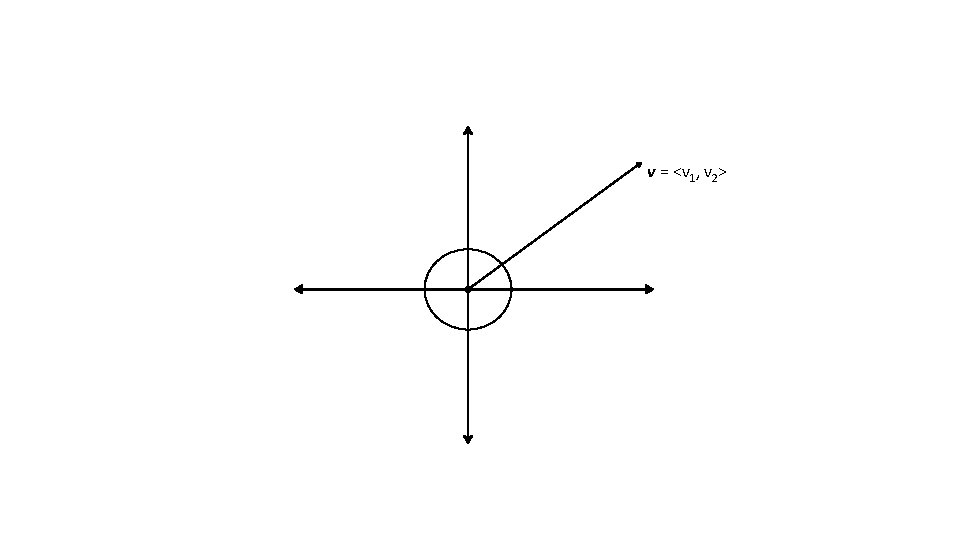
v = <v 1, v 2>

Finding Directional Angles •

Finding Directional Angles •

Writing Vectors Any vector can be defined by the following: v = <||v||cos θ, ||v||sin θ>

Determine the magnitude and direction of: <8, 6>, <-3, 5>


Vector Operations: <a, b> + <c, d> = <a + c, b + d> <a, b> - <c, d> = <a - c, b - d> k <a, b> = <ka, kb>

Resultant Force The Chair Example!

Resultant Force: Popper 20, Continued •

Resultant Force: Popper 20, Continued •

Resultant Force: Popper 20, Continued •

Resultant Force: Popper 20, Continued Two forces are acting on an object. The first has a magnitude of 10 and a direction of 30 o. The other has a magnitude of 5 and a direction of 45 o. Determine the magnitude and direction of their Resultant Force. Question 5: Magnitude of Resultant a. 14. 9 b. 4. 5 c. 20. 7 d. 1. 9

Resultant Force: Popper 20, Continued Two forces are acting on an object. The first has a magnitude of 10 and a direction of 30 o. The other has a magnitude of 5 and a direction of 45 o. Determine the magnitude and direction of their Resultant Force. Question 6: Direction of Resultant a. 55. 1 o b. 34. 9 o c. 44. 2 o d. 45. 8 o

Look at this situation graphically (parallelogram) or analytically (operations on vectors).

Unit Vectors To calculate a unit vector, u, in the direction of v you must calculate: u = (1/||v||)<v 1, v 2>.

Find the unit vector in the direction of the following: <3, 5> <1, 8>.

Linear Combination Form: Standard Unit Vectors: i = <1, 0> j = <0, 1>

Linear Combination Form: Standard Unit Vectors: i = <1, 0> j = <0, 1> If v = <v 1, v 2> = v 1 <1, 0> + v 2 <0, 1> = v 1 i + v 2 j

So convert the following w = <3, -5> into linear combination form.

The Dot Product of Two Vectors Vocabulary: Angle between vectors: The smallest angles between two vectors in standard position Orthogonal Vectors: Vectors that are at right angles.

Calculating the dot product of two vectors Consider u = <a, b> and v = <c, d> u · v = ac + bd

Determine value of <7, 5> · <9, -1> Determine value of <6, 1> · <-5, 3>

Angles between Vectors •

Determine the angle between the vectors: u = <9, 3>; and v = <4, 8>.

Determine the angle between the vectors: u = <0, 4>; and v = <3, 9>.

Give a possible vector that would be at a right angle to <7, -2>?

Give a possible vector that would be at a right angle to <7, -2>? What general rule can you use to determine orthogonal vectors?
 Software-defined networking: a comprehensive survey
Software-defined networking: a comprehensive survey Zuzana 1330
Zuzana 1330 Decreto 1330 de 2019 power point
Decreto 1330 de 2019 power point Engr 1330
Engr 1330 Opnav 5239 14
Opnav 5239 14 Engr 1330
Engr 1330 Ib math
Ib math Forwarding equivalence classes
Forwarding equivalence classes Mapping between s plane and z plane
Mapping between s plane and z plane 탄성계수
탄성계수 Topmarks
Topmarks Gấu đi như thế nào
Gấu đi như thế nào Số nguyên tố là số gì
Số nguyên tố là số gì Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Hệ hô hấp
Hệ hô hấp Tư thế ngồi viết
Tư thế ngồi viết Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Mật thư tọa độ 5x5
Mật thư tọa độ 5x5 Chụp tư thế worms-breton
Chụp tư thế worms-breton Tư thế ngồi viết
Tư thế ngồi viết ưu thế lai là gì
ưu thế lai là gì Thẻ vin
Thẻ vin Cái miệng nó xinh thế chỉ nói điều hay thôi
Cái miệng nó xinh thế chỉ nói điều hay thôi Thể thơ truyền thống
Thể thơ truyền thống Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Diễn thế sinh thái là
Diễn thế sinh thái là Lp html
Lp html Giọng cùng tên là
Giọng cùng tên là Phép trừ bù
Phép trừ bù Hát lên người ơi alleluia
Hát lên người ơi alleluia Sự nuôi và dạy con của hổ
Sự nuôi và dạy con của hổ đại từ thay thế
đại từ thay thế Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Công thức tính thế năng
Công thức tính thế năng Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Dạng đột biến một nhiễm là
Dạng đột biến một nhiễm là Lời thề hippocrates
Lời thề hippocrates