MATEMTICA Ensino Fundamental 9 Ano Equao do 2

MATEMÁTICA Ensino Fundamental, 9º Ano Equação do 2º grau resolução

MATEMÁTICA, 9º Ano Equação do 2º grau resolução BASE CURRICULAR COMUM PARA AS REDES PÚBLICAS DO ESTADO DE PERNAMBUCO - MATEMÁTICA Tem-se observado que uma abordagem das equações do segundo grau apenas pela aplicação direta da fórmula de Bhaskara termina por provocar dificuldades posteriores. Os alunos acabam tomando-a como método único e, quando “esquecem a fórmula”, não são capazes de resolver o problema. Assim, é recomendável que, nessa etapa, os alunos sejam incentivados a resolver equações de segundo grau utilizando a fatoração e o processo de completar quadrados, que, além de serem métodos eficazes podem dar significado à fórmula de Bhaskara. (Base Curricular Comum para as redes públicas do estado de Pernambuco , Matemática, 2008, página 99. ) CONTEÚDOS PROPOSTOS PARA O ENSINO DA MATEMÁTICA NO QUARTO CICLO: No trabalho com a Álgebra é fundamental a compreensão de conceitos como a formulação e a resolução de problemas por meio de equações (ao identificar parâmetros, incógnitas, variáveis) e o conhecimento da “sintaxe” (regras para resolução) de uma equação. (PCN, terceiro e quarto ciclos do ensino fundamental, Matemática, 1998, página 84)

MATEMÁTICA, 9º Ano Equação do 2º grau resolução RESOLVENDO EQUAÇÕES DO 2º GRAU SINTAM-SE TODOS CONVIDADOS A RESOLVER ALGUMAS EQUAÇÕES DO 2º GRAU VAMOS CHAMAR ESSE NÚMERO VOCÊS SÃO CAPAZES DE ME DESCONHECIDO (INCÓGNITA) DE X, LOGO RESPONDER QUAL É O NÚMERO QUE TEMOS A EQUAÇÃO: ELEVADO AO QUADRADO DÁ 25? X² = 25 PENSARAM NO NÚMERO 5 NÃO FOI? PARABÉNS!!!! EXISTE OUTRO NÚMERO QUE RESPONDE A ESSA PERGUNTA SABIAM? É O NÚMERO -5, OBSERVEM: PARA X = 5 TEMOS: PARA X = - 5 TEMOS: 5² = 5. 5 = 25 (-5)² = (-5) = 25 OBSERVE QUA A EXPRESSÃO X² = 25 É UMA EQUAÇÃO E COMO O EXPOENTE DA INCÓGNITA É 2, DIZEMOS QUE ELA É DO 2º GRAU E CONSEGUENTEMENTE POSSUI COMO SOLUÇÃO DOIS NÚMEROS.

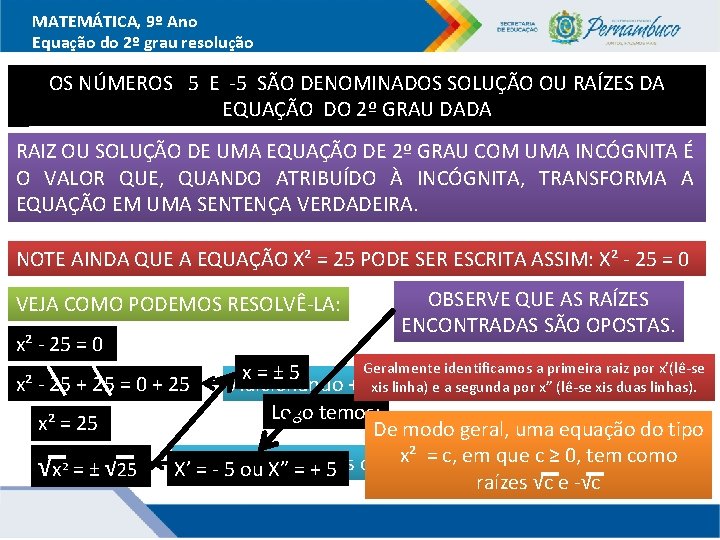
MATEMÁTICA, 9º Ano Equação do 2º grau resolução OS NÚMEROS 5 E -5 SÃO DENOMINADOS SOLUÇÃO OU RAÍZES DA EQUAÇÃO DO 2º GRAU DADA RAIZ OU SOLUÇÃO DE UMA EQUAÇÃO DE 2º GRAU COM UMA INCÓGNITA É O VALOR QUE, QUANDO ATRIBUÍDO À INCÓGNITA, TRANSFORMA A EQUAÇÃO EM UMA SENTENÇA VERDADEIRA. NOTE AINDA QUE A EQUAÇÃO X² = 25 PODE SER ESCRITA ASSIM: X² - 25 = 0 VEJA COMO PODEMOS RESOLVÊ-LA: x² - 25 = 0 OBSERVE QUE AS RAÍZES ENCONTRADAS SÃO OPOSTAS. Geralmente identificamos a primeira raiz por x’(lê-se x=± 5 x² - 25 + 25 = 0 + 25 Adicionando + 25 membros xis aos linha)dois e a segunda por x” (lê-se xis duas linhas). Logo temos: x² = 25 De modo geral, uma equação do tipo x² = c, em que c ≥ 0, tem como a raiz √x² = ± √ 25 X’Extraindo = - 5 ou X” = + nos 5 dois membros raízes √c e -√c

MATEMÁTICA, 9º Ano Equação do 2º grau resolução VEJA AINDA ESSA OUTRA EQUAÇÃO: AGORA OBSERVE COM ATENÇÃO: QUAL É A SOLUÇÃO DA EQUAÇÃO X² + 36 = 0? RESOLVENDO A EQUAÇÃO TEMOS: X² + 36 = 0 X² + 36 - 36 = 0 - 36 X² = - 36 2 X² - 18 = 0 RESOLVENDO-A TEMOS: 2 X² - 18 + 18 = 0 + 18 2 X² = 18 Adicionando + 18 aos dois membros Dividindo os indicar dois Observe que podemos por 2 e a também amembros primeira segunda raiz da equação por X 1 Adicionando – 36 aos dois. X²membros =9 e X 2, respectivamente. 2 X² = 18 2 2 √x ² = ± √ 9 Extraindo a raiz nos dois De modo geral, uma equação domembros tipo ax² + c = 0, com a ≠ 0, Extraindo a raiz nos dois membros √x² = ± √-36 X 1 = - 3 ou X 2 = + 3 pode ser transformada na equação ax² = - c, e esta em Não existe no conjunto dos números reais, ou X = √-36 x² = - c. seja, não existe um número real cujo quadraa do é um número negativo. Logo, ESSA EQUAÇÃO NÃO TEM SOLUÇÃO NO CONJUNTO DOS NÚMEROS REAIS

MATEMÁTICA, 9º Ano Equação do 2º grau resolução VAMOS TENTAR RESOLVER O SEGUINTE PROBLEMA : Luís tem um terreno na forma de um quadrado. Ele pretende comprar um terreno de 90 m² que faz divisa com o que ele já possui. Desse modo, ele ficaria com um terreno retangular de 414 m². Qual é a medida do lado do terreno de formato quadrado de Luís? REPRESENTANDO O NOVO TERRENO DE LUÍS POR UMA FIGURA : X X² X 90 m² EQUACIONANDO O PROBLEMA TEMOS: A área do terreno na forma de um quadrado corresponde a X². X² Luís pretende comprar um terreno de 90 m² + 90 Após a compra Luís ficará com um terreno de 414 m². = 414 X² + 90 = 414 Problema extraído do livro de Matemática: Bianchini/Edwaldo Bianchini, 7 ed. , São Paulo, Moderna, 2011, página 115.

MATEMÁTICA, 9º Ano Equação do 2º grau resolução RESOLVENDO A EQUAÇÃO TEMOS: COMO A MEDIDA DO LADO DEVE SER UM NÚMERO POSITIVO, CONCLUÍMOS: X² + 90 = 414 O LADO DO QUADRADO Adicionando - 90 MEDE aos dois membros 18 m. X² + 90 - 90 = 414 - 90 X² = 324 √X² = ± √ 324 X = ± 18 X’ = - 18 OU OBSERVE QUE A EQUAÇÃO X² + 90 = 414 Extraindo as raízes nos dois membros FOI REDUZIDA AO TIPO X² = C X’’ = + 18

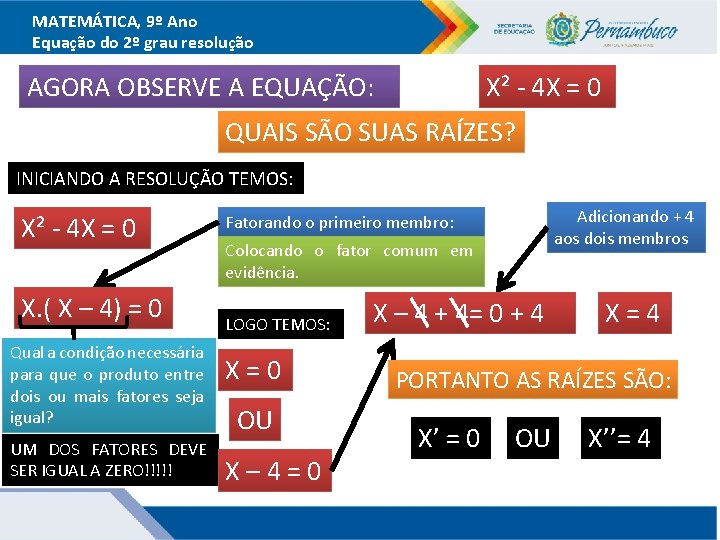
MATEMÁTICA, 9º Ano Equação do 2º grau resolução AGORA OBSERVE A EQUAÇÃO: X² - 4 X = 0 QUAIS SÃO SUAS RAÍZES? INICIANDO A RESOLUÇÃO TEMOS: X² - 4 X = 0 X. ( X – 4) = 0 Qual a condição necessária para que o produto entre dois ou mais fatores seja igual? UM DOS FATORES DEVE SER IGUAL A ZERO!!!!! Adicionando + 4 aos dois membros Fatorando o primeiro membro: Colocando o fator comum em evidência. LOGO TEMOS: X=0 OU X– 4=0 X – 4 + 4= 0 + 4 X=4 PORTANTO AS RAÍZES SÃO: X’ = 0 OU X’’= 4

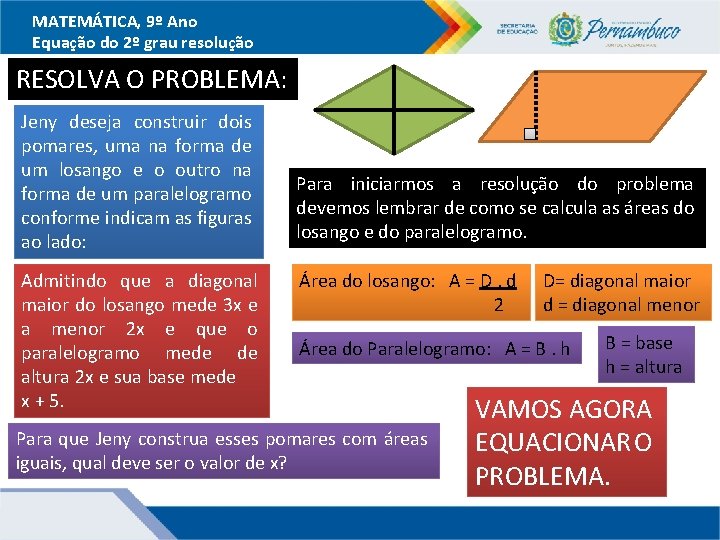
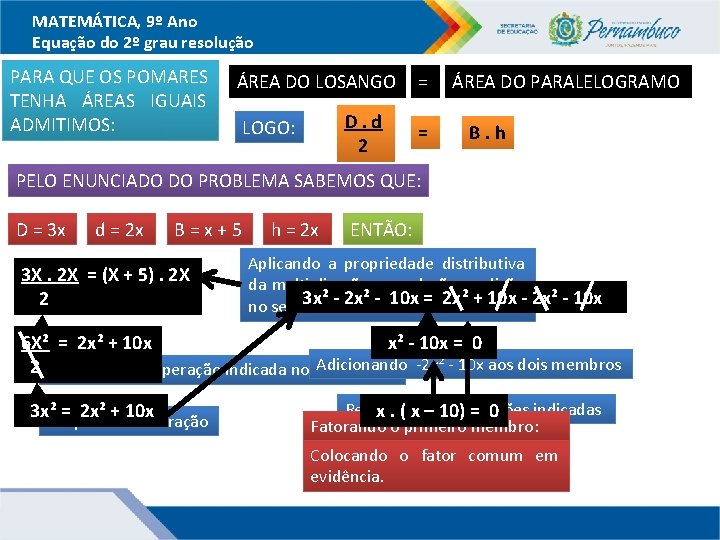
MATEMÁTICA, 9º Ano Equação do 2º grau resolução RESOLVA O PROBLEMA: Jeny deseja construir dois pomares, uma na forma de um losango e o outro na forma de um paralelogramo conforme indicam as figuras ao lado: Admitindo que a diagonal maior do losango mede 3 x e a menor 2 x e que o paralelogramo mede de altura 2 x e sua base mede x + 5. Para iniciarmos a resolução do problema devemos lembrar de como se calcula as áreas do losango e do paralelogramo. Área do losango: A = D. d 2 D= diagonal maior d = diagonal menor Área do Paralelogramo: A = B. h Para que Jeny construa esses pomares com áreas iguais, qual deve ser o valor de x? B = base h = altura VAMOS AGORA EQUACIONAR O PROBLEMA.

MATEMÁTICA, 9º Ano Equação do 2º grau resolução PARA QUE OS POMARES TENHA ÁREAS IGUAIS ADMITIMOS: ÁREA DO LOSANGO D. d 2 LOGO: = = ÁREA DO PARALELOGRAMO B. h PELO ENUNCIADO DO PROBLEMA SABEMOS QUE: D = 3 x d = 2 x B=x+5 3 X. 2 X = (X + 5). 2 X 2 h = 2 x ENTÃO: Aplicando a propriedade distributiva da multiplicação em relação a adição 3 x² -membro. 2 x² - 10 x = 2 x² + 10 x - 2 x² - 10 x no segundo 6 X² = 2 x² + 10 x x² - 10 x = 0 Adicionando -2 x² - 10 x aos dois membros 2 Resolvendo a operação indicada no numerador 3 x²Simplificando = 2 x² + 10 xa fração Resolvendo operações indicadas x. ( x –as 10) = 0 Fatorando o primeiro membro: Colocando o fator comum em evidência.

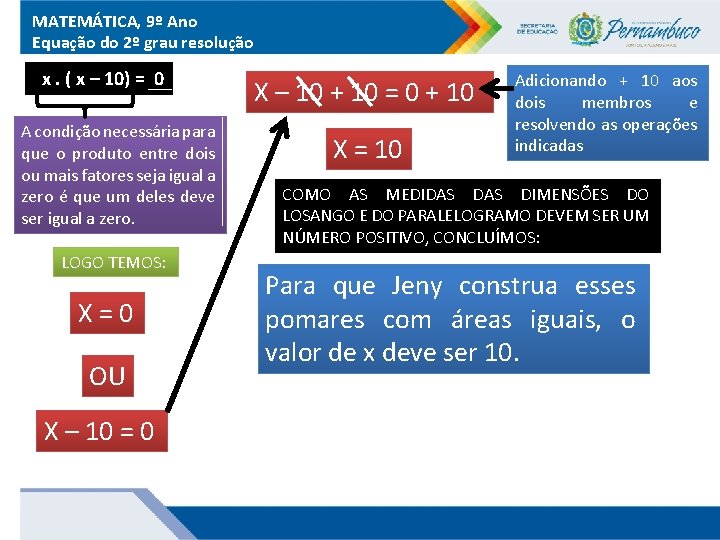
MATEMÁTICA, 9º Ano Equação do 2º grau resolução x. ( x – 10) = 0 A condição necessária para que o produto entre dois ou mais fatores seja igual a zero é que um deles deve ser igual a zero. LOGO TEMOS: X=0 OU X – 10 = 0 X – 10 + 10 = 0 + 10 X = 10 Adicionando + 10 aos dois membros e resolvendo as operações indicadas COMO AS MEDIDAS DIMENSÕES DO LOSANGO E DO PARALELOGRAMO DEVEM SER UM NÚMERO POSITIVO, CONCLUÍMOS: Para que Jeny construa esses pomares com áreas iguais, o valor de x deve ser 10.

MATEMÁTICA, 9º Ano Equação do 2º grau resolução De modo geral, uma equação do tipo ax² + b = 0, quando fatorada, recai na equação x. (ax + b) = 0. x’ = 0 ax² + bx = 0 = x. (ax + b) = 0 ax + b = 0 x’’ = - b , com a≠ 0 a

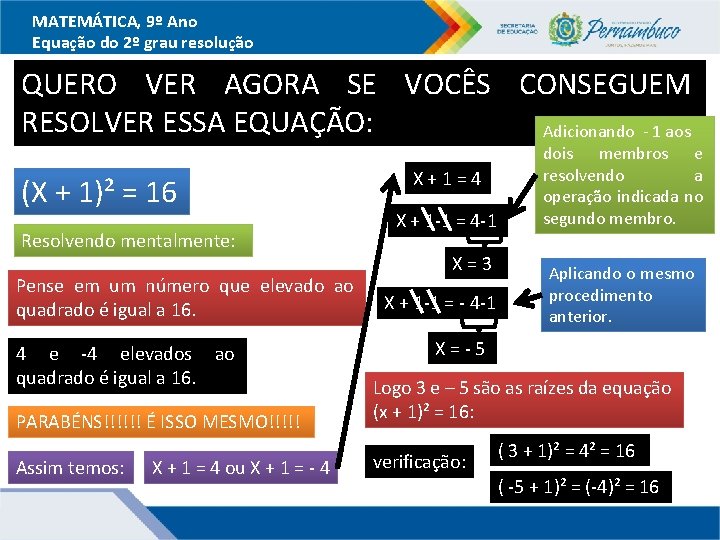
MATEMÁTICA, 9º Ano Equação do 2º grau resolução QUERO VER AGORA SE VOCÊS CONSEGUEM RESOLVER ESSA EQUAÇÃO: Adicionando - 1 aos (X + 1)² = 16 Resolvendo mentalmente: Pense em um número que elevado ao quadrado é igual a 16. 4 e -4 elevados ao quadrado é igual a 16. PARABÉNS!!!!!! É ISSO MESMO!!!!! Assim temos: X + 1 = 4 ou X + 1 = - 4 X+1=4 X + 1 -1 = 4 -1 X=3 X + 1 -1 = - 4 -1 dois membros e resolvendo a operação indicada no segundo membro. Aplicando o mesmo procedimento anterior. X=-5 Logo 3 e – 5 são as raízes da equação (x + 1)² = 16: verificação: ( 3 + 1)² = 4² = 16 ( -5 + 1)² = (-4)² = 16

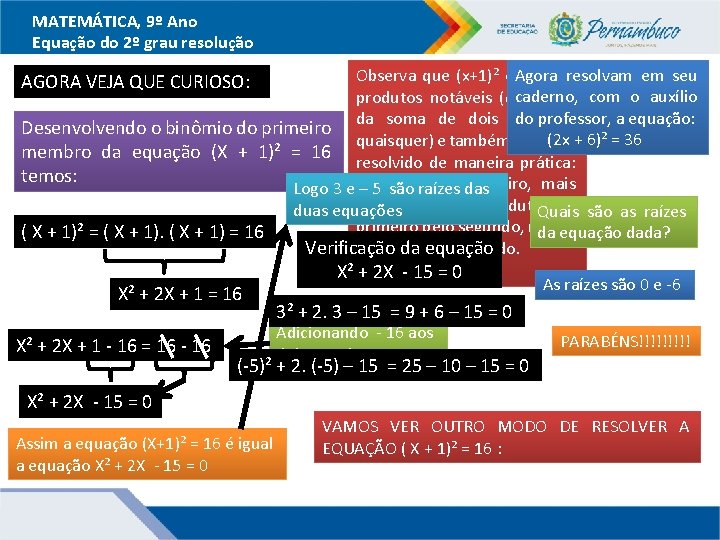
MATEMÁTICA, 9º Ano Equação do 2º grau resolução resolvam em seu Observa que (x+1)² é Agora um dos caderno, com o auxílio produtos notáveis (quadrado do professor, a equação: Desenvolvendo o binômio do primeiro da soma de dois números quaisquer) e também pode(2 x ser+ 6)² = 36 membro da equação (X + 1)² = 16 resolvido de maneira prática: temos: do das primeiro, mais Logo 3 e quadrado – 5 são raízes duas vezes o produto. Quais do são as raízes duas equações primeiro pelo segundo, mais o ( X + 1)² = ( X + 1) = 16 da equação dada? Verificação da equação quadrado do segundo. AGORA VEJA QUE CURIOSO: X² + 2 X + 1 = 16 X² + 2 X + 1 - 16 = 16 - 16 X² + 2 X - 15 = 0 As raízes são 0 e -6 3² + 2. 3 – 15 = 9 + 6 – 15 = 0 Adicionando - 16 aos dois membros PARABÉNS!!!!! (-5)² + 2. (-5) – 15 = 25 – 10 – 15 = 0 X² + 2 X - 15 = 0 Assim a equação (X+1)² = 16 é igual a equação X² + 2 X - 15 = 0 VAMOS VER OUTRO MODO DE RESOLVER A EQUAÇÃO ( X + 1)² = 16 :

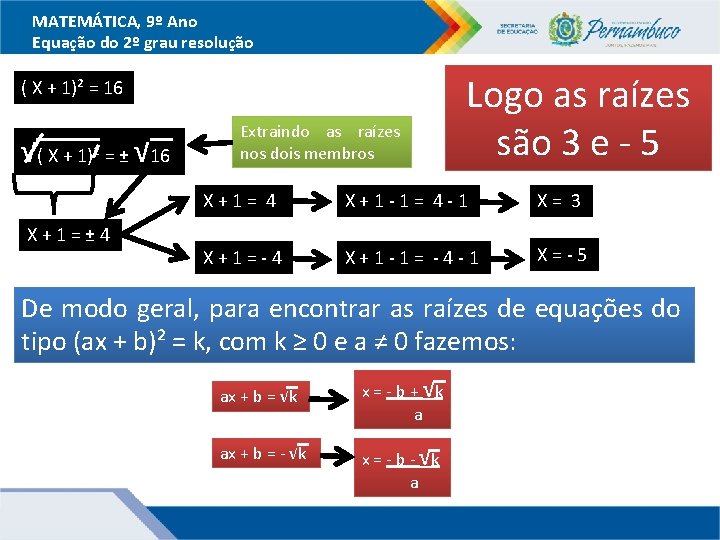
MATEMÁTICA, 9º Ano Equação do 2º grau resolução ( X + 1)² = 16 √( X + 1)² = ± √ 16 X+1=± 4 Extraindo as raízes nos dois membros Logo as raízes são 3 e - 5 X+1= 4 X+1 -1= 4 -1 X= 3 X+1=-4 X+1 -1= -4 -1 X=-5 De modo geral, para encontrar as raízes de equações do tipo (ax + b)² = k, com k ≥ 0 e a ≠ 0 fazemos: ax + b = √k ax + b = - √k x = - b + √k a x = - b - √k a

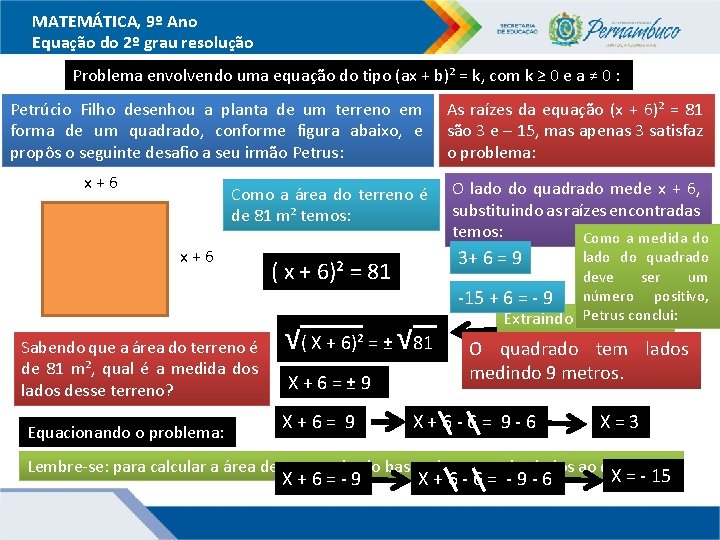
MATEMÁTICA, 9º Ano Equação do 2º grau resolução Problema envolvendo uma equação do tipo (ax + b)² = k, com k ≥ 0 e a ≠ 0 : Petrúcio Filho desenhou a planta de um terreno em forma de um quadrado, conforme figura abaixo, e propôs o seguinte desafio a seu irmão Petrus: x+6 Como a área do terreno é de 81 m² temos: x+6 Sabendo que a área do terreno é de 81 m², qual é a medida dos lados desse terreno? Equacionando o problema: √( X + 6)² = ± √ 81 X+6= 9 O lado do quadrado mede x + 6, substituindo as raízes encontradas temos: Como a medida do 3+ 6 = 9 ( x + 6)² = 81 X+6=± 9 As raízes da equação (x + 6)² = 81 são 3 e – 15, mas apenas 3 satisfaz o problema: lado do quadrado deve ser um -15 + 6 = - 9 número positivo, conclui: Extraindo Petrus as raízes nos dois membros O quadrado tem lados medindo 9 metros. X+6 -6= 9 -6 X=3 Lembre-se: para calcular a área de um quadrado basta elevar um dos lados ao quadrado. X+6=-9 X+6 -6= -9 -6 X = - 15

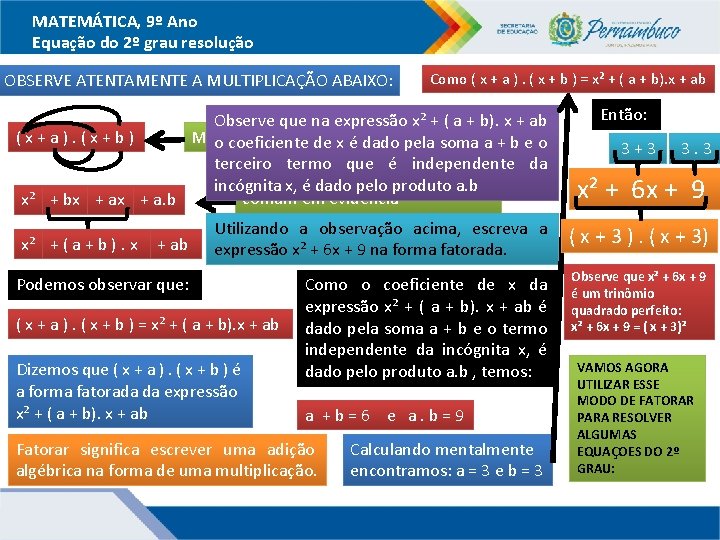
MATEMÁTICA, 9º Ano Equação do 2º grau resolução OBSERVE ATENTAMENTE A MULTIPLICAÇÃO ABAIXO: Como ( x + a ). ( x + b ) = x² + ( a + b). x + ab Observe que na expressão x² + ( a + b). x + ab (x+a). (x+b) Multiplicando osde binômios temos: o coeficiente x é dado pela soma a + b e o terceiro termo que é independente da Fatorando: colocando o fator incógnita x, é dado pelo produto a. b comum em evidência x² + bx + a. b x² + ( a + b ). x + ab Então: 3+3 3. 3 x² + 6 x + 9 Utilizando a observação acima, escreva a expressão x² + 6 x + 9 na forma fatorada. ( x + 3 ). ( x + 3) Como o coeficiente de x da expressão x² + ( a + b). x + ab é dado pela soma a + b e o termo independente da incógnita x, é dado pelo produto a. b , temos: Observe que x² + 6 x + 9 é um trinômio quadrado perfeito: x² + 6 x + 9 = ( x + 3)² Podemos observar que: ( x + a ). ( x + b ) = x² + ( a + b). x + ab Dizemos que ( x + a ). ( x + b ) é a forma fatorada da expressão x² + ( a + b). x + ab a +b=6 e a. b=9 Fatorar significa escrever uma adição algébrica na forma de uma multiplicação. Calculando mentalmente encontramos: a = 3 e b = 3 VAMOS AGORA UTILIZAR ESSE MODO DE FATORAR PARA RESOLVER ALGUMAS EQUAÇOES DO 2º GRAU:

MATEMÁTICA, 9º Ano Equação do 2º grau resolução Resolva a equação x² + 10 x + 25 = 0 2º modo de resolução: Já sabemos ( x + aequação ). ( x + bé )da = x² + ( a + b). x + ab Perceba que essa forma ax² + bx + c = 0, onde a = 1, b = 10 e c = 25. Então: a + b = 10 e a. b = 25 Calculando mentalmente: a = 5 e b = 5 Logo, x² + 10 x + 25 = ( x + 5 ) = 0 1º modo de resolução: (x+5)=0 x+5 =0 ou x+5 -5=0 -5 X’ = - 5 (x+5)=0 Extraindo as raízes ( x + 5 )² = 0 nos dois membros √( x + 5)² = ± √ 0 (x+5)=± 0 Tem duas soluções iguais, logo: x+5 =0 Para que o produto entre dois fatores seja igual a +5 -5=0 -5 zero, um dos fatores deve serxzero x+5 =0 x+5 -5=0 -5 X’’ = - 5 São duas soluções iguais x =-5 Logo asmembros raízes são x’ = - 5 ou x ‘’ = - 5 Adicionando – 5 aos dois Verificação: (-5)² + 10. (-5) + 25 = 25 – 50 + 25 = 0 VEJAMOS MAIS UMA EQUAÇÃO:

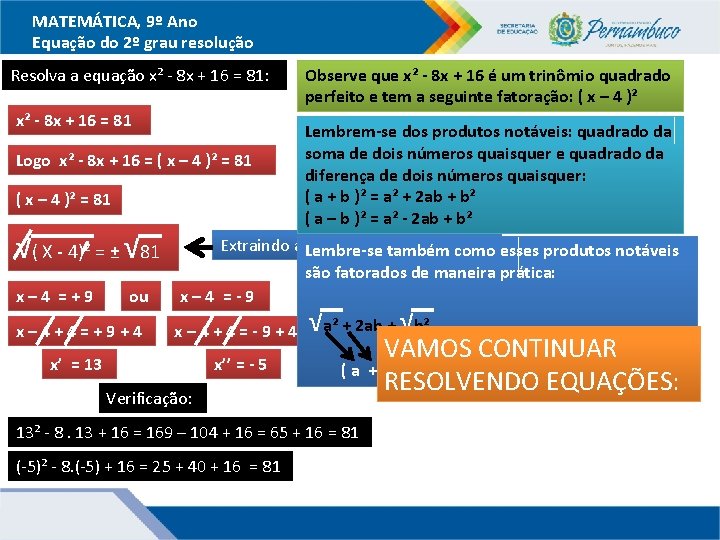
MATEMÁTICA, 9º Ano Equação do 2º grau resolução Resolva a equação x² - 8 x + 16 = 81: Observe que x² - 8 x + 16 é um trinômio quadrado perfeito e tem a seguinte fatoração: ( x – 4 )² x² - 8 x + 16 = 81 Lembrem-se dos produtos notáveis: quadrado da soma de dois números quaisquer e quadrado da Logo x² - 8 x + 16 = ( x – 4 )² = 81 diferença de dois números quaisquer: ( a + b )² = a² + 2 ab + b² ( x – 4 )² = 81 ( a – b )² = a² - 2 ab + b² Extraindo as. Lembre-se raízes nos também dois membros como esses produtos notáveis ( X - 4)² = ± 81 √ √ x– 4 =+9 ou são fatorados de maneira prática: x– 4 =-9 x– 4+4=+9+4 x– 4+4=-9+4 x’ = 13 x’’ = - 5 Verificação: √a² +Adicionando 2 ab + √b² + 4 aos dois membros VAMOS CONTINUAR ( a + b )² RESOLVENDO EQUAÇÕES: 13² - 8. 13 + 16 = 169 – 104 + 16 = 65 + 16 = 81 (-5)² - 8. (-5) + 16 = 25 + 40 + 16 = 81

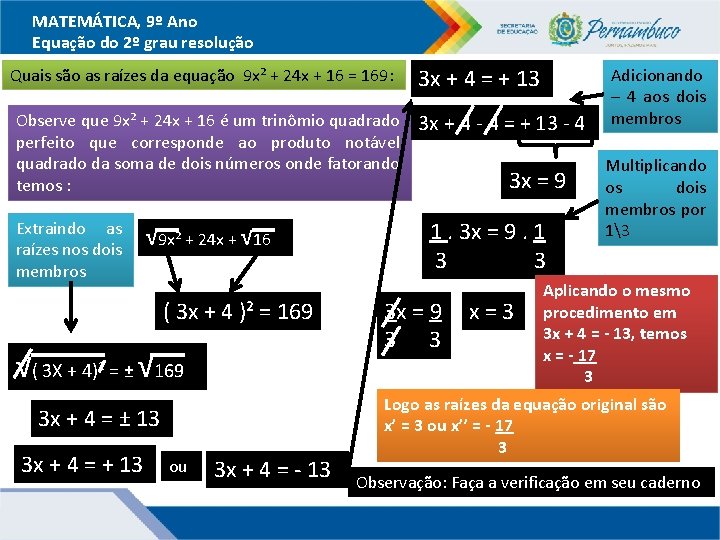
MATEMÁTICA, 9º Ano Equação do 2º grau resolução Quais são as raízes da equação 9 x² + 24 x + 16 = 169: Observe que 9 x² + 24 x + 16 é um trinômio quadrado perfeito que corresponde ao produto notável quadrado da soma de dois números onde fatorando temos : Extraindo as raízes nos dois membros √ 9 x² + 24 x + √ 16 ( 3 x + 4 )² = 169 √( 3 X + 4)² = ± √ 169 3 x + 4 = ± 13 3 x + 4 = + 13 ou 3 x + 4 = - 13 3 x + 4 = + 13 3 x + 4 - 4 = + 13 - 4 3 x = 9 1. 3 x = 9. 1 3 3 3 x = 9 3 3 x=3 Adicionando – 4 aos dois membros Multiplicando os dois membros por 13 Aplicando o mesmo procedimento em 3 x + 4 = - 13, temos x = - 17 3 Logo as raízes da equação original são x’ = 3 ou x’’ = - 17 3 Observação: Faça a verificação em seu caderno

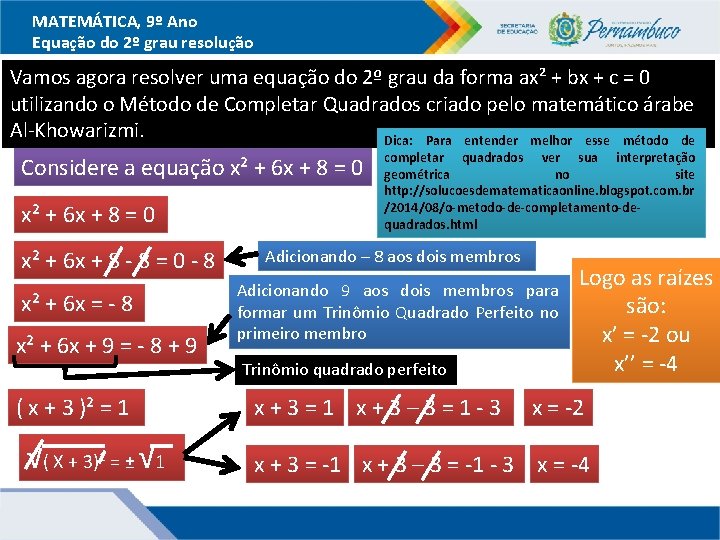
MATEMÁTICA, 9º Ano Equação do 2º grau resolução Vamos agora resolver uma equação do 2º grau da forma ax² + bx + c = 0 utilizando o Método de Completar Quadrados criado pelo matemático árabe Al-Khowarizmi. Dica: Para entender melhor esse método de Considere a equação x² + 6 x + 8 = 0 x² + 6 x + 8 - 8 = 0 - 8 x² + 6 x = - 8 x² + 6 x + 9 = - 8 + 9 ( x + 3 )² = 1 √( X + 3)² = ± √ 1 completar quadrados ver sua interpretação geométrica no site http: //solucoesdematicaonline. blogspot. com. br /2014/08/o-metodo-de-completamento-dequadrados. html Adicionando – 8 aos dois membros Adicionando 9 aos dois membros para formar um Trinômio Quadrado Perfeito no primeiro membro Trinômio quadrado perfeito x+3=1 x+3– 3=1 -3 Logo as raízes são: x’ = -2 ou x’’ = -4 x = -2 x + 3 = -1 x + 3 – 3 = -1 - 3 x = -4

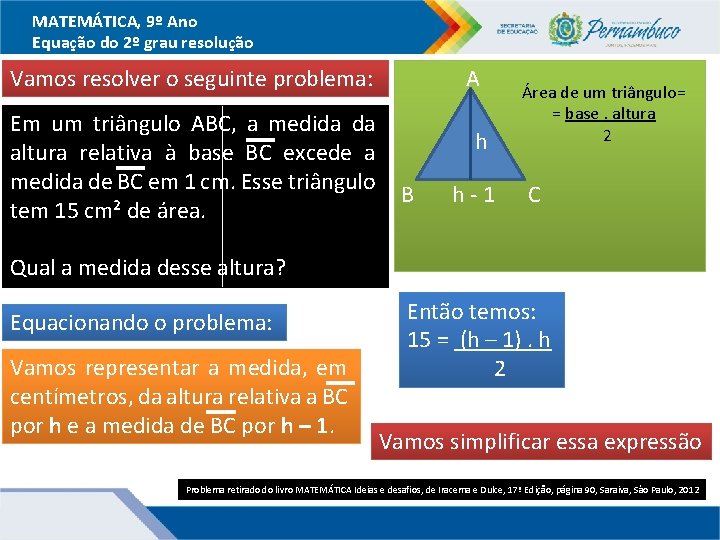
MATEMÁTICA, 9º Ano Equação do 2º grau resolução Vamos resolver o seguinte problema: Em um triângulo ABC, a medida da altura relativa à base BC excede a medida de BC em 1 cm. Esse triângulo tem 15 cm² de área. A h B h-1 Área de um triângulo= = base. altura 2 C Qual a medida desse altura? Equacionando o problema: Vamos representar a medida, em centímetros, da altura relativa a BC por h e a medida de BC por h – 1. Então temos: 15 = (h – 1). h 2 Vamos simplificar essa expressão Problema retirado do livro MATEMÁTICA Ideias e desafios, de Iracema e Dulce, 17ª Edição, página 90, Saraiva, Sâo Paulo, 2012

MATEMÁTICA, 9º Ano Equação do 2º grau resolução Vamos resolver a equação h² – h – 30 = 0 utilizando uma fórmula de um famoso matemático Hindu chamado Bhaskara. 15 = (h – 1). h 2 15. 2 = (h – 1). h. 2 2 30 = (h – 1). h 30 = h² - h Multiplicando membros por Para resolveros adoisequação ax² 2 e+ bx + c = 0, simplificando com a ≠ 0 usamos a fórmula de Bhaskara: Resolvendo as operações indicadas Observação: A expressão b² - 4 ac representada Aplicando a propriedade distributiva x = - b ± b² - 4. a. c pela letra grega delta(∆) da multiplicação em relação éachamada discriminante 2. a subtração) da equação 30 – 30 = h² – h – 30 = 0 Equação do 2º grau completa √ ou x = - b ± √∆ , em que ∆ = b² - 4. a. c Adicionando – 30 aos dois membros 2. a Uma condição para a existência de soluções reais é que o discriminante da equação seja maior ou igual a zero. Logo: ∆ < 0, então a equação NÃO POSSUI RAIZ REAL ∆ > 0, então a equação tem DUAS RAÍZES REAIS DIFERENTES ∆ = 0, então a equação DUAS RAÍZES REAIS IGUAIS

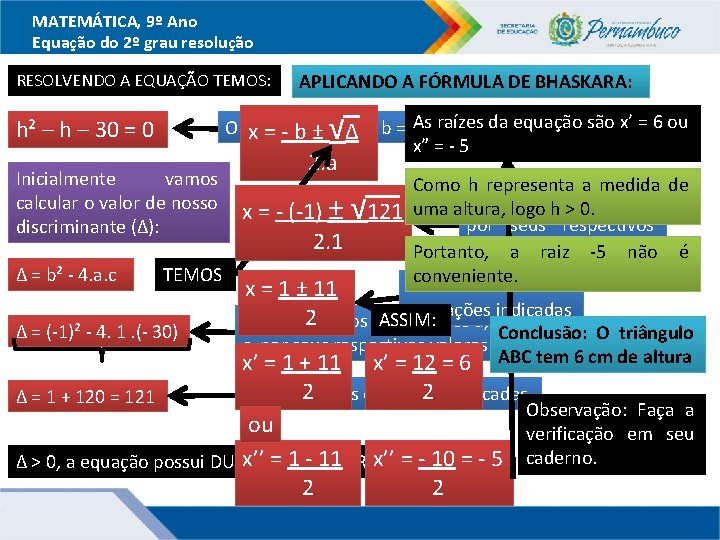
MATEMÁTICA, 9º Ano Equação do 2º grau resolução RESOLVENDO A EQUAÇÃO TEMOS: √ Aseraízes da equação são x’ = 6 ou Observe c = - 30 x = - bque ± a ∆= 1, b = -1 x” = - 5 h² – h – 30 = 0 Inicialmente vamos calcular o valor de nosso discriminante (∆): ∆ = b² - 4. a. c APLICANDO A FÓRMULA DE BHASKARA: TEMOS ∆ = (-1)² - 4. 1. (- 30) 2. a x = - (-1) ± 2. 1 √ Como h representa a medida de Substituindo logo h > a, 0. b e ∆ 121 uma altura, por seus respectivos valores Portanto, a raiz -5 não é conveniente. Resolvendo as x = 1 ± 11 operações indicadas 2 os coeficientes ASSIM: Substituindo a, b e c por seus respectivos valores Conclusão: O triângulo ABC tem 6 cm de altura x’ = 1 + 11 x’ = 12 = 6 2 as operações 2 indicadas Resolvendo ∆ = 1 + 120 = 121 Observação: Faça a ou verificação em seu x’’RAÍZES = 1 - 11 x’’ = - 10 = - 5 caderno. ∆ > 0, a equação possui DUAS DIFERENTES 2 2

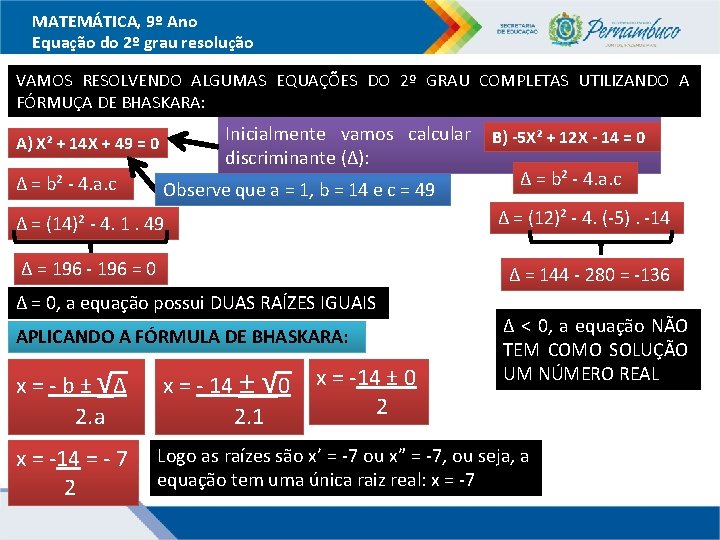
MATEMÁTICA, 9º Ano Equação do 2º grau resolução VAMOS RESOLVENDO ALGUMAS EQUAÇÕES DO 2º GRAU COMPLETAS UTILIZANDO A FÓRMUÇA DE BHASKARA: Inicialmente vamos calcular o. B) valor de - 14 nosso -5 X² + 12 X =0 discriminante (∆): ∆ = b² - 4. a. c Observe que a = 1, b = 14 e c = 49 ∆ = (12)² - 4. (-5). -14 ∆ = (14)² - 4. 1. 49 A) X² + 14 X + 49 = 0 ∆ = 196 - 196 = 0 ∆ = 144 - 280 = -136 ∆ = 0, a equação possui DUAS RAÍZES IGUAIS APLICANDO A FÓRMULA DE BHASKARA: ∆ < 0, a equação NÃO TEM COMO SOLUÇÃO UM NÚMERO REAL x = - b ± √∆ 2. a x = - 14 ± √ 0 2. 1 x = -14 = - 7 2 Logo as raízes são x’ = -7 ou x” = -7, ou seja, a equação tem uma única raiz real: x = -7 x = -14 ± 0 2

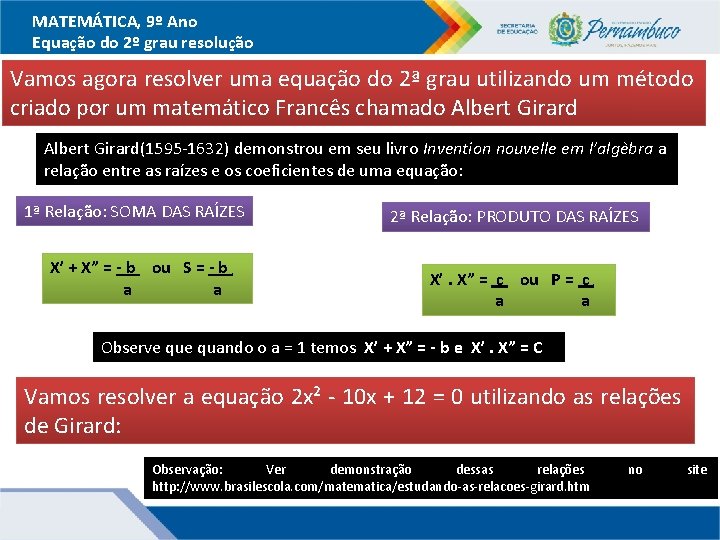
MATEMÁTICA, 9º Ano Equação do 2º grau resolução Vamos agora resolver uma equação do 2ª grau utilizando um método criado por um matemático Francês chamado Albert Girard(1595 -1632) demonstrou em seu livro Invention nouvelle em l’algèbra a relação entre as raízes e os coeficientes de uma equação: 1ª Relação: SOMA DAS RAÍZES X’ + X” = - b ou S = - b a a . 2ª Relação: PRODUTO DAS RAÍZES X’. X” = c ou P = c a a . Observe quando o a = 1 temos X’ + X” = - b e X’. X” = C Vamos resolver a equação 2 x² - 10 x + 12 = 0 utilizando as relações de Girard: Observação: Ver demonstração dessas relações http: //www. brasilescola. com/matematica/estudando-as-relacoes-girard. htm no site

MATEMÁTICA, 9º Ano Equação do 2º grau resolução Na equação 2 x² - 10 x + 12 = 0 temos a = 2, b = - 10 e c = 12 Segundo Girard: X’ + X” = - b a X’. X” = c e a . . . As expressões nos mostram que existem dois números que somados dá 5 e multiplicados dá 6 QUAIS SÃO ESSES NÚMEROS? Assim: X’ + X” = - (-10) 2 X’. X” = 12 2 . . . X’ + X” = 5 X’. X” = 6 Os números são 2 e 3 PARABÉNS!!! . . Assim as raízes são x’= 2 ou x”= 3 VERIFICAÇÃO: . . 2. 2² - 10. 2 + 12 = 8 – 20 + 12 = 0 Podemos encontrar as raízes da equação interpretando essas duas 2. 3² - 10. 3 + 12 = 18 – 30 + 12 = 0 expressões encontradas: X’ + X” = 5 X’. X” = 6. .

MATEMÁTICA, 9º Ano Equação do 2º grau resolução Vamos resolver a equação x² + 8 x + 15 = 0 utilizando as relações de Girard: Na equação x² + 8 x + 15 = 0 temos a = 1, b = 8 e c = 15 X’ + X” = - b a X’. X” = c e a . . Assim: X’ + X” = - 8 1 As expressões nos mostram que existem dois números que somados dá - 8 e multiplicados dá 15 QUAIS SÃO ESSES NÚMEROS? Os números são -3 e - 5 X’ + X” = - 8 Assim as raízes são x’= - 3 ou x”= -5 . . X’. X” = 15 1 . . X’. X” = 15 VERIFICAÇÃO: (-3)² + 8. (-3) + 15 = 9 – 24 + 15 = 0 (-5)² + 8. (-5) + 15 = 25 – 40 + 15 = 0

MATEMÁTICA, 9º Ano Equação do 2º grau resolução ATIVIDADES DE FIXAÇÃO: 1)Resolva as seguintes equações: a) X² - 225 = 0 b) X² + 19 = 100 c) 3 X² - 13 = 35 2) Determine as raízes destas equações: a) X² - 8 X = 0 b) 2 X² + 10 X = 0 c) 3 t² - t = 0 3)Determine os valores reais de x que verificam as equações: a) (X + 3)² = 64 b) (X - 5)² = 121 c) (X + 11)² = 324 4) Resolva a equação x² - 10 x + 21 = 0 utilizando: a) Fatoração b) Completamento de quadrado c) Fórmula de Bhaskara d) Relação de Girard

MATEMÁTICA, 9º Ano Equação do 2º grau resolução GABARITO DAS ATIVIDADES DE FIXAÇÃO: 1) : 3 a) x’= -15 ou x”= 15 b) x’= -9 ou x”= 9 c) x’= -4 ou x”= 4 a) x’= 5 ou x”= -11 b) x’= 16 ou x”= -6 c) x’= 7 ou x”= -29 2) a) x’= 0 ou x”= 8 b) x’= 0 ou x”= -5 c) t’= 0 ou t”= 13 4) x’= 3 ou x”= 7

MATEMÁTICA, 9º Ano Equação do 2º grau resolução SUGESTÃO DE ATIVIDADE PESQUISA NA INTERNET: Pesquisar problemas em disciplina como Física, Química e Biologia que utilizem em suas resoluções equações do 2º grau como ferramenta. Observação: Os físicos estabelecem leis que podem determinar a altura h que um objeto atingi em cada instante t, e utilizam a fórmula h = vt – gt² , onde h = altura, v = velocidade inicial do corpo, 2 g = aceleração da gravidade e t = tempo decorrido. Considerando h= 20 m, v = 25 m/s e g= 10 m/s² temos: 20 = 25 – 10 t² que simplificando é igual a t² – 5 t + 4 = 0 2 EQUAÇÃO DO 2º GRAU

MATEMÁTICA, 9º Ano Equação do 2º grau resolução BIBLIOGRAFIA -Parâmetros para a Educação Básica de Pernambuco, 2012. -PCN, terceiro e quarto ciclos do ensino fundamental, Matemática, 1998, página 84) -Behrens, Marilda Aparecida, O paradigma emergente e a prática pedagógica, 4ª edição, Petrópolis-RJ, Vozes, 2010. -Iracema Mori, Dulce Satiko Onaga, Matemática: ideias e desafios, 9º ano, 17. ed. -São Paulo: Saraiva, 2012. -Mazzieiro, Alceu dos Santos, Descobrindo e aplicando a matemática: 9º ano, Belo Horizonte: Dimensão, 2012. -Projeto Araribá, matemática obra coletiva, 8ª série, 1 ed. , São Paulo, Moderna, 2006. -Bigode, Antônio José Lopes, Matemática hoje é feita assim, 8ª série, São Paulo, FTD, 2000. -Bonjorno, José Roberto, Matemática: fazendo a diferença, 8ª série, 1 ed, São Paulo, FTD, 2006. -Giovanni, José Ruy, Matemática pensar e descobrir: o + novo, 8ª série , São Paulo, FTD, 2002. -www. somatematica. com. br -http: //tvescola. mec. gov. br/ - http: //www. brasilescola. com/matematica/estudando-as-relacoes-girard. htm -www. matematicoteca. blogspot. com. br/2011/08/tipos-de-matrizes. html -http: //solucoesdematicaonline. blogspot. com. br/2014/08/o-metodo-de-completamento-dequadrados. html