MATEMTICA Ensino Mdio 1 Ano Equao logartmica Matemtica

MATEMÁTICA Ensino Médio, 1º Ano Equação logarítmica

Matemática, 1º Ano, Equação logarítmica Neide pegou um empréstimo no valor de R$ 6 000, 00 e o pagou 1 ano depois, com o valor corrigido para R$ 7 609, 45. Ela deseja saber agora qual foi a taxa de juros aplicada na transação, sabendo que os juros foram calculados, a cada mês, em cima do montante do mês anterior, ou seja, foram juros compostos. Você sabia que com uma calculadora científica, ou uma boa tábua de logaritmos, e o conhecimento da fórmula de juros compostos Neide pode resolver esse problema? Veja isso a seguir!

Matemática, 1º Ano, Equação logarítmica Expressões logarítmicas Uma expressão diz-se logarítmica quando é calculável por meio de logaritmos. Exemplos: log 15 + log 33 log x − log y 5 ∙ log (x + 4)

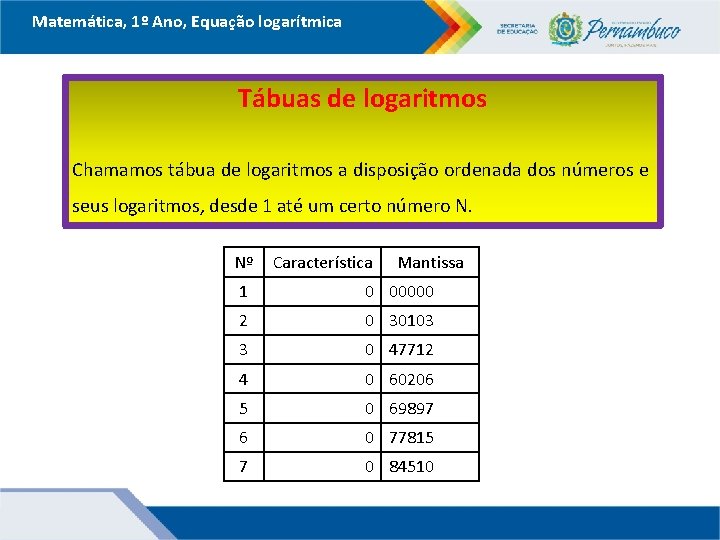
Matemática, 1º Ano, Equação logarítmica Tábuas de logaritmos Chamamos tábua de logaritmos a disposição ordenada dos números e seus logaritmos, desde 1 até um certo número N. Nº Característica Mantissa 1 0 00000 2 0 30103 3 0 47712 4 0 60206 5 0 69897 6 0 77815 7 0 84510

Matemática, 1º Ano, Equação logarítmica Denomina-se equação logarítmica àquela em que uma ou mais incógnitas estão subordinadas ao símbolo logaritmo. Exemplos: log 15 + log 33 = x log x − log y = 3 5 ∙ log (x + 4) = 2

Matemática, 1º Ano, Equação logarítmica Ao resolvermos uma equação desse tipo, devemos verificar as condições de existência do logaritmo. Além dessa verificação, aplicaremos a seguinte propriedade: loga b = loga c b = c, com a > 0, b > 0, c > 0 e a 1 E, ainda, utilizaremos as propriedades dos logaritmos.

Matemática, 1º Ano, Equação logarítmica Exemplos: log 10 x = 2 log 10 + log x = 2 1 + log x = 2 (logc ab = logc a + logc b) (loga an = n) log x = 2 − 1 log x = 1 Então: x = 101 (definição de logaritmo) x = 10

Matemática, 1º Ano, Equação logarítmica O problema de Neide Vamos, então, resolver o problema de Neide: C = R$ 6 000, 00 t = 1 ano = 12 meses M = R$ 7 609, 45 Logo, pela fórmula de juros compostos, teremos: 7 609, 45 = 6 000 ∙ (1 + i)12 = 7 609, 45 6 000 (1 + i)12 ≈ 1, 26824

Matemática, 1º Ano, Equação logarítmica Fazendo 1 + i = x, teremos: x 12 = 1, 26824 Aplicando logaritmos nos dois membros, teremos: log x 12 = log 1, 26824 12 ∙ log x = log 1, 26824 log x = 0, 1032 12 log x = 0, 0086 Portanto: x = 100, 0086 x = 1, 02

Matemática, 1º Ano, Equação logarítmica Como x = 1 + i, então: 1 + i = 1, 02 – 1 i = 0, 02 Ou seja i = 2% ao mês

Matemática, 1º Ano, Equação logarítmica Atividades resolvidas 1) Resolva em R as seguintes equações: a) log 2 (x – 3) = 1 b) logx− 2 (2 x – 4) = 2 c) log (x 2 – 1) = log (2 x – 1) d) (log 3 x)2 + log 3 x = 2 e) log 2 8 x + 5 = 3 x– 4

Matemática, 1º Ano, Equação logarítmica a) Condição de existência: x – 3 > 0 x>3 Resolvendo a equação, temos: Log 2 (x – 3) = 1 x – 3 = 21 x– 3=2 x=2+3 x=5 Como x = 5 satisfaz a condição de existência, temos: S = {5}

Matemática, 1º Ano, Equação logarítmica b) Condições de existência: 2 x – 4 > 0 2 x > 4 x > 2 x– 2>0 x>2 ex– 2 1 x 1+2 x 3 Logo, resolvendo a equação, temos: logx− 2 (2 x – 4) = 2 (x – 2)2 = 2 x – 4 x 2 – 4 x + 4 = 2 x – 4 x 2 – 4 x – 2 x + 4 = 0 x 2 – 6 x + 8 = 0

Matemática, 1º Ano, Equação logarítmica Daí: D = (− 6)² − 4 ∙ 1 ∙ 8 D = 36 − 32 D=4 x = − (− 6) 2∙ 1 . x 1 = 6 − 2 = 4 = 2 2 2 x 2 = 6 + 2 = 8 = 4 2 2 Nesse caso, como somente x 2 satisfaz as condições de existência, temos: S = {4}

Matemática, 1º Ano, Equação logarítmica c) Condições de existência: x 2 – 1 > 0 x < − 1 ou x > 1 2 x – 1 > 0 2 x > 1 x > ½ Resolvendo a equação, temos: log (x 2 – 1) = log (2 x – 1) x 2 – 1 = 2 x – 1 x 2 – 2 x = 0 x(x – 2) = 0 x 1 = 0 ou x 2 – 2 = 0 → x 2 = 2 Nesse caso, como somente x 2 satisfaz a condição de existência, então: S = {2}

Matemática, 1º Ano, Equação logarítmica d) Condição de existência: x > 0 Fazendo y = log 3 x, temos: y 2 + y = 2 y 2 + y – 2 = 0 Daí: D = 1² − 4 ∙ 1 ∙ (− 2) D=1+8 D=9

Matemática, 1º Ano, Equação logarítmica y=− 1 . 2∙ 1 y 1 = − 1 − 3 = − 4 = − 2 2 2 y 2 = − 1 + 3 = 2 = 1 2 2 Retornando o valor de y na igualdade y = log 3 x, temos: y 1 = − 2 log 3 x 1 = − 2 x 1 = 3− 2 x 1 = 1. 9

Matemática, 1º Ano, Equação logarítmica y 2 = 1 log 3 x 2 = 1 x 2 = 3 Nesse caso, como x 1 e x 2 satisfazem a condição de existência, temos: S = {1/9, 3} e) Condições de existência: 8 x + 5 > 0 8 x + 5 = 0 x– 4=0

Matemática, 1º Ano, Equação logarítmica Logo: x < − 5 ou x > 4 8 Segue que: log 2 8 x + 5 = 3 23 = 8 x + 5 8(x – 4) = 8 x + 5 x– 4 8 x – 32 = 8 x + 5 8 x – 8 x = 5 + 32 0 = 37 (impossível) Portanto: S=

Matemática, 1º Ano, Equação logarítmica 2) Resolva a equação log 4 x + logx 4 = 2. Condição de existência: x > 0 e x 1. Fazendo a mudança de base, para logx 4, teremos: log 4 x + log 4 4 = 2 log 4 x + 1 =2 log 4 x fazendo, agora, y = log 4 x, temos: y + 1 =2 y ou seja: y 2 – 2 y + 1 = 0

Matemática, 1º Ano, Equação logarítmica Assim: y 1 = y 2 = 1 Retornando o valor de y na igualdade y = log 4 x, temos: log 4 x = 1 Logo: x = 41 x=4 Como 4 satisfaz as condições de existência, temos: S = {4}

Matemática, 1º Ano, Equação logarítmica 3) Resolva as equações: a) logx 36 = 2 b) log 2 (x 2 + x + 2) = 3 c) log 2 [log 3 (x – 1)] = 2 a) Condição de existência: x > 0 e x 1 Pela definição de logaritmo, temos: x 2 = 36 x= 6 Como apenas x = 6 satisfaz a condição de existência, temos: S = {6}

Matemática, 1º Ano, Equação logarítmica b) Condição de existência: x 2 + x + 2 > 0 D= 12 – 4 ∙ 1 ∙ 2 D= 1 – 8 D= − 7 + + + + + Portanto: x R. Resolvendo a equação, temos: x 2 + x + 2 = 23 x 2 + x + 2 – 8 = 0 x 2 + x – 6 = 0

Matemática, 1º Ano, Equação logarítmica D= 12 – 4 ∙ 1 ∙ (− 6) D= 1 + 24 D= 25 x=− 1 5 2∙ 1 x’ = − 1 − 5 = − 6 = − 3 2 2 x” = − 1 + 5 = 4 = 2 2 2 Como x = − 3 e x = 2 satisfazem a condição de existência, temos: S = {− 3, 2}

Matemática, 1º Ano, Equação logarítmica c) Condição de existência: log 3 (x – 1) > 0 x– 1>1 x>2 Resolvendo a equação, temos: log 2 [log 3 (x – 1)] = 2 log 3 (x – 1) = 22 log 3 (x – 1) = 4 x – 1 = 34 x – 1 = 81 x = 82 Como x = 82 satisfaz a condição de existência, temos: S = {82}

Matemática, 1º Ano, Equação logarítmica Atividades Propostas 1) Resolva, em R, as seguintes equações: a) log 2 (4 x + 5) = log 2 (2 x + 11) b) log 3 (5 x 2 – 6 x + 16) = log 3 (4 x 2 + 4 x – 5) c) logx (2 x – 3) = logx (− 4 x + 8) d) log(x + 2) (x 2 – 2 x) = log(x + 2) 3 2) Resolva, em R, as seguintes equações: a) log 4 (x + 3) = 2 b) log 2 x (6 x 2 – 13 x + 15) = 2

Matemática, 1º Ano, Equação logarítmica 3) Sejam p e q, respectivamente, as soluções das equações: log 2 (log 3 x) = − 1 e log 5 [log 4 (214 + 10 x)] = 1. Qual é o valor de logp q? 4) Resolva, em R, as seguintes equações: a) log 2 (x – 2) + log 2 x = 3 b) 2 log 7 (x + 3) = log 7 (x 2 + 45) c) log (4 x – 1) – log (x + 2) = log x d) 3 log 5 2 + log 5 (x – 1) = 0 e) log x + log x 2 + log x 3 = − 6

Matemática, 1º Ano, Equação logarítmica 5) Aumentando um número x de 8 unidades, seu logaritmo em base 4 aumenta de meia unidade. Qual é o valor de x? 6) Resolva, em R, as equações: a) log 5 x = logx 5 b) log 49 7 x = logx 7 c) log 6 x 2 = logx 36

Matemática, 1º Ano, Equação logarítmica LINKS https: //www. youtube. com/watch? v=7 Pe. NXm. N 3 mo 0 https: //www. youtube. com/watch? v=v 31 UWHdy. V 74 https: //www. youtube. com/watch? v=inh. Xy-qob 3 k http: //www. brasilescola. com/matematica/equacoeslogaritmicas. htm http: //www. fund 198. ufba. br/expo/eq-ine. pdf