Lecture 9 Security of RSA THE MAGIC WORDS
















![Pollard’s Rho Method • Fastest known in 1977 [Pollard 75] • To find factor Pollard’s Rho Method • Fastest known in 1977 [Pollard 75] • To find factor](https://slidetodoc.com/presentation_image/4ffb01757d4d999f88c93c5171a74fdd/image-18.jpg)









![To factor r [RSA-129] we assembled the largest collaboration yet seen in computational number To factor r [RSA-129] we assembled the largest collaboration yet seen in computational number](https://slidetodoc.com/presentation_image/4ffb01757d4d999f88c93c5171a74fdd/image-28.jpg)



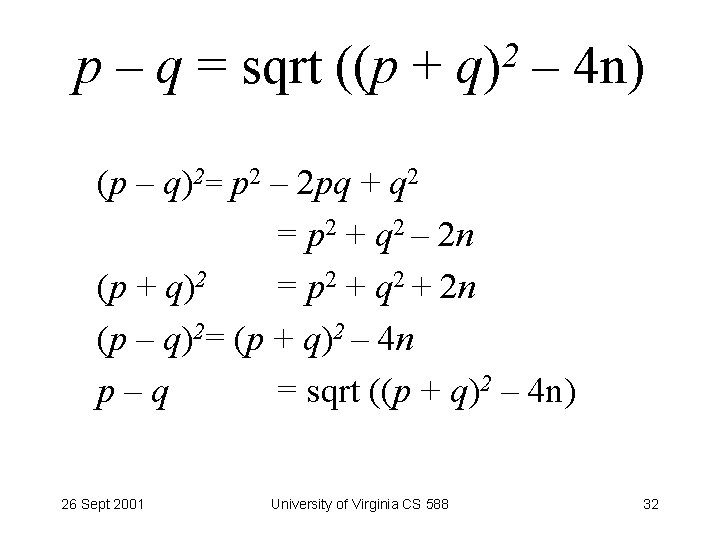








- Slides: 40

Lecture 9: Security of RSA THE MAGIC WORDS ARE SQUEAMISH OSSIFRAGE. Because both the system’s privacy and the security of digital money depend on encryption, a breakthrough in mathematics or computer science that defeats the cryptographic system could be a disaster. The obvious mathematical breakthrough would be development of an easy way to factor large prime numbers. Any person or organization possessing this power could counterfeit money, penetrate any personal, corporate, or government file, and possibly even undermine the security of nations. Bill Gates, The Road Ahead CS 588: Security and Privacy David Evans University of Virginia 26 Sept 2001 University of Virginia CS 588 http: //www. cs. virginia. edu/~evans Computer Science

Menu • Finding Big Pseudo Primes • Security of RSA – Factoring 26 Sept 2001 University of Virginia CS 588 2

Properties of E and D Trap-door one way function: 1. D (E (M)) = M 2. E and D are easy to compute. 3. Revealing E doesn’t reveal an easy way to compute D Trap-door one way permutation: also 4. E (D (M)) = M 26 Sept 2001 University of Virginia CS 588 3

Property 2: Easy to Compute • We need large “random” primes p and q • Are there enough primes? • How can we find them? 26 Sept 2001 University of Virginia CS 588 4

How many prime numbers? • Infinite (proved by Euclid, 300 BC) • Proof by contradiction: Suppose that there exist only finitely many primes p 1 < p 2 <. . . < pr. Let N = (p 1)(p 2). . . (pr) + 1 N > pr so it is composite, N = p * M If p = pi for some 1…r, then, N = pi * M = pi * (p 1)(p 2). . . (pi-1) (pi+1). . . (pr) + 1 pi (M - (p 1)(p 2). . . (pi-1) (pi+1). . . (pr)) = 1 Contradiction: pi > 1 Hence, there must be infinitely many primes. 26 Sept 2001 University of Virginia CS 588 5

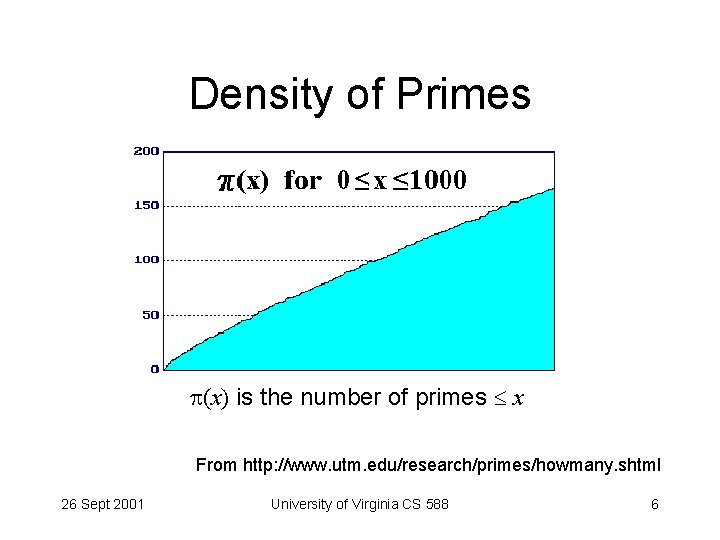
Density of Primes (x) is the number of primes x From http: //www. utm. edu/research/primes/howmany. shtml 26 Sept 2001 University of Virginia CS 588 6

Approximating (x) • The Prime Number Theorem: (x) ~ x/ln x – Difficult to prove (first conjectured by Legendre in 1798 by looking at table of values) • How many guesses to find a prime bigger than x? – About ln x/2 guesses • (Naïvely) Each guess requires sqrt(x) work • For 200 digits: 230 guesses * 10100 – More work than breaking 3 DES! 26 Sept 2001 University of Virginia CS 588 7

Need a faster prime test • There are several fast probabilistic prime tests • Can quickly test a prime with high probability, with a small amount of work • If we pick a non-prime, its not a disaster (exercise for reader, will be on PS 3) 26 Sept 2001 University of Virginia CS 588 8

Fermat Test • Recall Fermat’s Little Theorem: If n is prime and a is not divisible by n then an-1 1 mod n • Prove n is composite by finding an-1 1 mod n • Showing an-1 1 mod n does not prove it is prime • But if it holds for many a’s it is likely than n is prime – Holds for all a’s for some non-primes known as Carmichael Numbers: 561, 645, 1105, …) • Better prime test: Miller-Rabin – Probability n is prime 1 – ¼k 26 Sept 2001 University of Virginia CS 588 9

Properties of E and D Trap-door one way function: 1. D (E (M)) = M 2. E and D are easy to compute. 3. Revealing E doesn’t reveal an easy way to compute D Trap-door one way permutation: also 4. E (D (M)) = M 26 Sept 2001 University of Virginia CS 588 10

Property 4: E (D (M)) = M D(M) = Md mod n E(D(M)) = (Md mod n)e mod n = Mde mod n = Med mod n = M (from the property 1 proof) 26 Sept 2001 University of Virginia CS 588 11

Properties of E and D Trap-door one way function: 1. 2. D (E (M)) = M E and D are easy to compute. 3. Revealing E doesn’t reveal an easy way to compute D Trap-door one way permutation: also 4. E (D (M)) = M Are there other functions that have properties 1, 2 and 4? 26 Sept 2001 University of Virginia CS 588 12

RSA E(M) = Me mod n D(C) = Cd mod n n = pq p, q are prime d is relatively prime to (p – 1)(q – 1) ed 1 (mod (p – 1)(q – 1)) 26 Sept 2001 University of Virginia CS 588 13

Revealing E doesn’t reveal D • Revealing E: e, n. • Can attacker find D? • If attacker factors n = p * q ed 1 mod (p – 1)(q – 1) Easy to find d e-1 mod (p – 1)(q – 1) • Use experience to argue factoring is hard. • Argue all other attacks are at least as hard as factoring n. 26 Sept 2001 University of Virginia CS 588 14

Gardner’s Column: Original RSA challenge ($100) n (RSA-129) = 1 1438 1625 7578 8886 7669 2357 7997 6146 6120 1021 8296 7212 4236 2562 5618 4293 5706 9352 4573 3897 8305 9712 3563 9587 0505 8989 0751 4759 9290 0268 7954 3541 e = 9007 C = 9686 9613 7546 2206 1477 1409 2225 4355 8829 0575 9991 1245 7431 9874 6951 2093 0816 2982 2514 5708 3569 3147 6622 8839 8962 8013 3919 9055 1829 9451 5781 5154 Scientific American, August 1977 26 Sept 2001 University of Virginia CS 588 15

400000000 17 Ron Rivest (1977): factoring n (129 digits) would require at least 40 quadrillion years if you could do a * b mod c in one nanosecond. Derek Atkins (April 1994): We are happy to announce that RSA-129 = 3490 5295 1084 7650 9491 4784 9619 9038 9813 3417 7646 3849 3387 8439 9082 0577 * 3 2769 1329 9326 6709 5499 6198 8190 8344 6141 3177 6429 6799 2942 5397 9828 8533 26 Sept 2001 University of Virginia CS 588 16

Trial and Error Factoring • Guess x, if 1 < gcd (x, n) < n then x is an interesting factor • If p and q are similar size, lowest factor is around n. – Requires O( n) divisions. – For RSA-129 = 1. 1 * 1064 divisions, 1 per nanosecond = 3. 4 * 1047 years 26 Sept 2001 University of Virginia CS 588 17
![Pollards Rho Method Fastest known in 1977 Pollard 75 To find factor Pollard’s Rho Method • Fastest known in 1977 [Pollard 75] • To find factor](https://slidetodoc.com/presentation_image/4ffb01757d4d999f88c93c5171a74fdd/image-18.jpg)
Pollard’s Rho Method • Fastest known in 1977 [Pollard 75] • To find factor p, requires 4 p modular multiplies • Worst case: lowest p is n, we need 4 n multiplies • For RSA-129 = 1. 3 * 1032 = 4 * 1015 years • Rivest probably used this, but made a math error (4 quadrilllion 40 quadrilllion) 26 Sept 2001 University of Virginia CS 588 18

How so Fast • Better factoring algorithms • Distributed computation • Still can’t do a * b mod c in one nanosecond (not faster processors) – 1 ns = 10 -9 s – Best Pentium 4 today: 2 GHz (cycle =. 5 ns) – But, multiplying 100 digit numbers takes many cycles 26 Sept 2001 University of Virginia CS 588 19

Fermat Factoring • Factor 8051 • Hint: (½ (a + b))2 – (½(a – b))2 = ¼ (a 2 + 2 ab + b 2) - ¼ (a 2 - 2 ab + b 2) = ½ ab + ½ ab = ab • 8051 = 8100 – 49 = 902 – 72 • 8051 = 97 83 ½ (83 + 97) = 90 ½ (83 – 97) = 7 26 Sept 2001 University of Virginia CS 588 20

Fermat Factoring • Any odd composite integer can be written as n = u 2 - v 2 • To factor n, start looking for u and v around n • Is this less work than trial and error division? No, only in lucky cases where factor is near n 26 Sept 2001 University of Virginia CS 588 21

Kraitchik’s Enhancement • Instead of looking for u and v such that n = u 2 - v 2 look for any multiple of n: n = (u 2 - v 2)k or: u 2 v 2 mod n • Some solutions uninteresting: u v mod n • Others (½) are interesting: u v mod n n divides u 2 - v 2 = (u – v) (u + v) but not (u – v) or (u + v) gcd (u – v, n) and gcd (u + v, n) are factors of n 26 Sept 2001 University of Virginia CS 588 22

Kraitchik, cont. For x’s near n Q(x) = x 2 – n Try to find x’s where: Q(x 1) Q(x 2) …Q(xk) = v 2 x 1 x 2 …xk = u Then, x 12 x 22 …xk 2 = u 2 (x 12 – n) … (xk 2 – n) mod n v 2 mod n But, how do we find the x’s? 26 Sept 2001 University of Virginia CS 588 23

Finding the x’s • Some of the Q(x)’s are easy to factor • From these, find products that are squares n = 2041 462 = 2116 Q(46) = 75 = 3 52 Looking for: 3 Q(47) = 168 = 2 3 7 2 Q(x ) …Q(x ) = v 1 2 k Q(48) = 263 (hard to factor) x 1 x 2 …xk = u Q(49) = 360 = 23 32 5 Q(50) = 459 = 33 17 Q(51) = 560 = 24 5 7 Q(46) Q(47) Q(49) Q(51) = 23+3+4 34 54 72 = (25 32 52 7)2 Example from [Pomerance 96] 26 Sept 2001 University of Virginia CS 588 24

Finding the Factors Q(46) Q(47) Q(49) Q(51) = (25 32 52 7)2 v 2 u = 46 47 49 51 = 311 mod 2041 v = 25 32 52 7 = 1416 mod 2041 u 2 = v 2 mod 2041 311 1416 mod 2041 So, gcd (1416 – 311, 2041) is a factor of 2041. gcd (1105, 2041) = gcd (2041, 1105 mod 2041) = gcd (1105, 2041 mod 1105) = gcd (1105, 936) = gcd (936, 1105 mod 936) = gcd (936, 169) = gcd (169, 936 mod 169) = gcd (169, 91) = gcd (91, 169 mod 91) = gcd (91, 78) = gcd (78, 91 mod 78) = gcd (78, 13) = gcd (13, 78 mod 13) = gcd (13, 13) = 13 26 Sept 2001 University of Virginia CS 588 25

Factoring Pragmatics • Conjectured to take esqrt(2 log n) steps to factor n. • Quadratic Sieve Factoring – Improved Kraitchik’s algorithm to choose likely good values for x’s – Complexity: esqrt(log n) – How much bigger numbers can it factor? Twice as many digits in same time! 26 Sept 2001 University of Virginia CS 588 26

Breaking RSA-129 • Organized by Derek Atkins and others, 1994 • Quadratic Sieve algorithm • Memory-limited (1994 – most workstations 16 MB RAM), used 10 M to hold. 5 M primes • Recruited volunteers from Internet • 1600 machines • Used 5000 MIPS years over 8 months 26 Sept 2001 University of Virginia CS 588 27
![To factor r RSA129 we assembled the largest collaboration yet seen in computational number To factor r [RSA-129] we assembled the largest collaboration yet seen in computational number](https://slidetodoc.com/presentation_image/4ffb01757d4d999f88c93c5171a74fdd/image-28.jpg)
To factor r [RSA-129] we assembled the largest collaboration yet seen in computational number theory and, possibly, performed the largest single computation ever completed. In several important respects, the resources we had available were barely adequate for the task. Consequently, ingenuity and diplomacy were required for the successful completion of the project. Derek Atkins, Michael Graff, et. al. , The Magic Words Are Squeamish Ossifrage, Asia. Crypt 1994. 26 Sept 2001 University of Virginia CS 588 28

Recent Factoring Algorithms • Team from CWI (Amsterdam) factored RSA-155 (512 bits), August 1999 • Number Field Sieve (Sneakers) • ~8000 MIPS years (36 CPU years) • 7 months on ~300 machines • Lecture 1: factor 300 digit number for automatic A. How much harder is this? 26 Sept 2001 University of Virginia CS 588 29

RSA Security • Factoring is hard (except in Sneakers) • Is this enough to know RSA is secure? • Can you compute D without factoring n? – Probably not, but can’t prove it. – But, can prove other obvious mathematical attacks are equivalent to factoring. 26 Sept 2001 University of Virginia CS 588 30

(n) without factoring • Calculate (n) without factoring n. ed 1 mod (n) • Equivalent to factoring: (n) = (p – 1)(q – 1) = n – (p + q) + 1 p + q = n – (n) – 1 p – q = sqrt ((p + q)2 – 4 n) [next slide] 2 p = sqrt ((n – (n) – 1)2 – 4 n) + n – (n) – 1 If we know (n) we can calculate p and q easily. 26 Sept 2001 University of Virginia CS 588 31
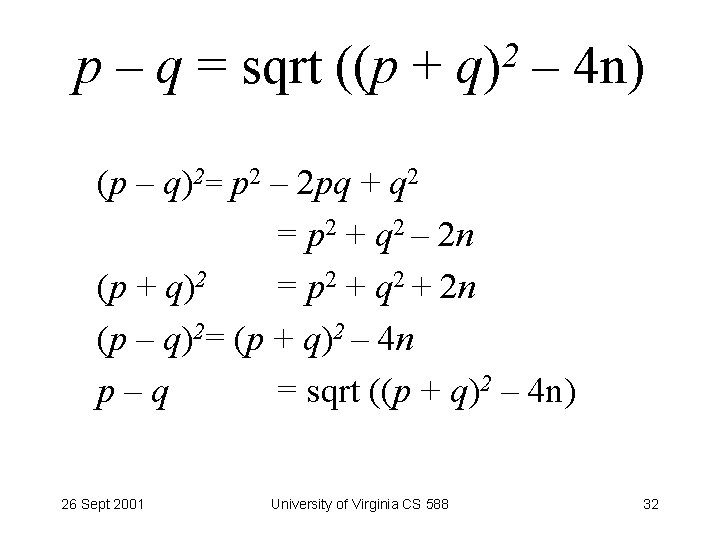
p – q = sqrt ((p 2 + q) – 4 n) (p – q)2= p 2 – 2 pq + q 2 = p 2 + q 2 – 2 n (p + q)2 = p 2 + q 2 + 2 n (p – q)2= (p + q)2 – 4 n p – q = sqrt ((p + q)2 – 4 n) 26 Sept 2001 University of Virginia CS 588 32

Determine d without (n) • Brute force: m digits long, amount of work is 10 m. – Try 1 T/second (special purpose hardware) – Will take 3*1030 years for m = 50. – For factoring difficulty, m > 100. (Bigger than AES key) • Non-brute force: knowing d enables factoring. 26 Sept 2001 University of Virginia CS 588 33

Determining d factoring ed = 1 mod (n) k * (n) = ed – 1 Already showed, finding as factoring. Also true for multiple of (n) is same (n). 26 Sept 2001 University of Virginia CS 588 34

Properties of RSA’s E and D • Trap-door one way function: D (E (M)) = M E and D are easy to compute. Revealing E doesn’t reveal an easy way to compute D • Trap-door one way permutation: also E (D (M)) = M 26 Sept 2001 University of Virginia CS 588 35

Applications of RSA • Privacy: – Bob encrypts message to Alice using EA – Only Alice knows DA • Signatures: – Alice encrypts a message to Alice using DA – Bob decrypts using EA – Knows it was from Alice, since only Alice knows DA • Things you use every day: ssh, SSL, DNS, etc. • More than 400, 000 copies of the RSA algorithm are currently installed 26 Sept 2001 University of Virginia CS 588 36

Two “Questionable” Statements in RSA Paper “(The NBS scheme (DES) is probably somewhat faster if special-purposed hardware encryption devices are used; our scheme may be faster on a general -purpose computer since multiprecision arithmetic operations are simpler to implement than complicated bit manipulations. )” (p. 4) 26 Sept 2001 University of Virginia CS 588 37

Two “Questionable” Statements in RSA Paper “The need for a courier between every pair of users has thus been replaced by the requirement for a single secure meeting between each user and the public file manager when the user joins the system. ” (p. 6) 26 Sept 2001 University of Virginia CS 588 38

Who really invented RSA? • General Communications HQ, Cheltenham (formed from Bletchley Park after WWII) • 1969 – James Ellis asked to work on key distribution problem • Secure telephone conversations by adding “noise” to line: – Receiver could add the noise and subtract it – No need for sender to have key! • Late 1969 – idea for PK, but no function • Clifford Cocks invented function (RSA) 26 Sept 2001 University of Virginia CS 588 39

Charge • Next time: what to do about all those couriers! • Project Pre-Proposals due Monday • They should include: – Clear topic description and plan: the more details you can provide on what you plan to do, the better feedback I can provide – Related Work • Summary of what you have found so far • Reading list: things you plan to read next 26 Sept 2001 University of Virginia CS 588 40
 Rsa the magic words
Rsa the magic words Private securit
Private securit Rsa compliance
Rsa compliance Rsa algorithm in cryptography and network security
Rsa algorithm in cryptography and network security 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Computer security 161 cryptocurrency lecture
Computer security 161 cryptocurrency lecture Magic words drawing
Magic words drawing Ted nicholas net worth
Ted nicholas net worth Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Ng-html
Ng-html Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Voi kéo gỗ như thế nào
Voi kéo gỗ như thế nào Glasgow thang điểm
Glasgow thang điểm Hát lên người ơi alleluia
Hát lên người ơi alleluia Các môn thể thao bắt đầu bằng tiếng đua
Các môn thể thao bắt đầu bằng tiếng đua Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công thức tiính động năng
Công thức tiính động năng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Mật thư tọa độ 5x5
Mật thư tọa độ 5x5 Làm thế nào để 102-1=99
Làm thế nào để 102-1=99 Phản ứng thế ankan
Phản ứng thế ankan Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thể thơ truyền thống
Thể thơ truyền thống Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Một số thể thơ truyền thống
Một số thể thơ truyền thống Cái miệng xinh xinh thế chỉ nói điều hay thôi
Cái miệng xinh xinh thế chỉ nói điều hay thôi Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau Thế nào là sự mỏi cơ
Thế nào là sự mỏi cơ đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ V cc
V cc Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể Fecboak
Fecboak Thẻ vin
Thẻ vin đại từ thay thế
đại từ thay thế điện thế nghỉ
điện thế nghỉ Tư thế ngồi viết
Tư thế ngồi viết Diễn thế sinh thái là
Diễn thế sinh thái là Các loại đột biến cấu trúc nhiễm sắc thể
Các loại đột biến cấu trúc nhiễm sắc thể Số.nguyên tố
Số.nguyên tố