Lecture 05 ITS 033 Programming Algorithms DivideandConquer Approach

Lecture 05 ITS 033 – Programming & Algorithms Divide-and-Conquer Approach Asst. Prof. Dr. Bunyarit Uyyanonvara IT Program, Image and Vision Computing Lab. School of Information and Computer Technology Sirindhorn International Institute of Technology Thammasat University http: //www. siit. tu. ac. th/bunyarit@siit. tu. ac. th 02 5013505 X 2005 1

ITS 033 Topic 01 - Problems & Algorithmic Problem Solving Topic 02 – Algorithm Representation & Efficiency Analysis Topic 03 - State Space of a problem Topic 04 - Brute Force Algorithm Topic 05 - Divide and Conquer Topic 06 - Decrease and Conquer Topic 07 - Dynamics Programming Topic 08 - Transform and Conquer Topic 09 - Graph Algorithms Topic 10 - Minimum Spanning Tree Topic 11 - Shortest Path Problem Topic 12 - Coping with the Limitations of Algorithms Power http: //www. siit. tu. ac. th/bunyarit/its 033. php and http: //www. vcharkarn. com/vlesson/showlesson. php? lessonid=7 2

This Week Overview n n n Divide & Conquer Mergesort Quicksort Binary search Closest Pair by Divide and Conquer 3

Lecture 05. 0 ITS 033 – Programming & Algorithms Divide & Conquer: Introduction Asst. Prof. Dr. Bunyarit Uyyanonvara IT Program, Image and Vision Computing Lab. School of Information and Computer Technology Sirindhorn International Institute of Technology Thammasat University http: //www. siit. tu. ac. th/bunyarit@siit. tu. ac. th 02 5013505 X 2005 4

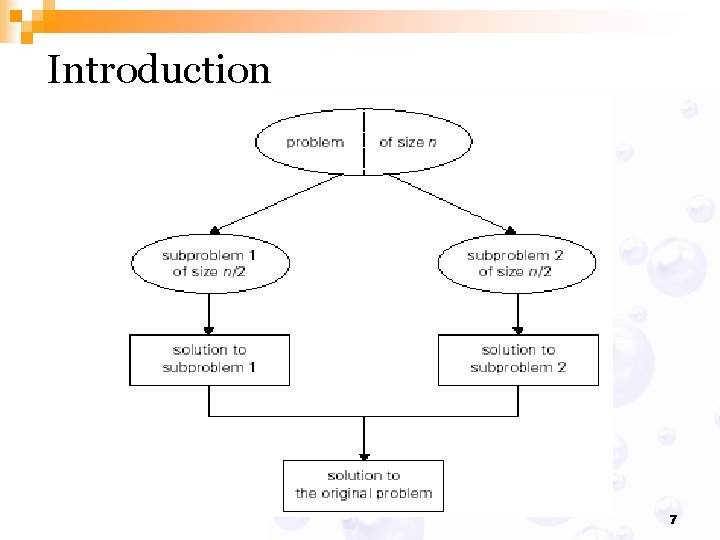
Introduction n Divide-and-conquer algorithms work according to the following general plan: 1. A problem’s instance is divided into several smaller instances of the same problem, ideally of about the same size. 2. The smaller instances are solved (typically recursively, though sometimes a different algorithm is employed when instances become small enough). 3. If necessary, the solutions obtained for the smaller instances are combined to get a solution to the original problem. 5

Divide-and-Conquer n n Divide-and conquer is a general algorithm design paradigm: ¨ Divide: n divide the input data S in two disjoint subsets S 1 and S 2 ¨ Recur: n solve the subproblems associated with S 1 and S 2 ¨ Conquer: n combine the solutions for S 1 and S 2 into a solution for S The base case for the recursion are subproblems of size 0 or 1 6

Introduction 7

Introduction n Not every divide-and-conquer algorithm is necessarily more efficient than even a brute-force solution. n An instance of size n can be divided into several instances of size n/b, with a of them needing to be solved. (Here, a and b are constants; a = 1 and b > 1. ). Assuming that size n is a power of b, to simplify our analysis, we get the following recurrence for the running time T (n): T (n) = a. T (n/b) + f (n), (4. 1) n where f (n) is a function that accounts for the time spent on dividing the problem into smaller ones and on combining their solutions. 8

Introduction n n Recurrence (4. 1) is called the general divideand- conquer recurrence. The order of growth of its solution T (n) depends on the values of the constants a and b and the order of growth of the function f (n) 9

Introduction 10

Introduction n For example, the recurrence equation for the number of additions A(n) made by the divideand-conquer summation algorithm on inputs of size n = 2 k is A(n) = 2 A(n/2) + 1. n Thus, for this example, a = 2, b = 2, and d = 0; hence, since a >bd, A(n) Є θ(nlogb a) = θ (nlog 2 2) = θ (n). 11

Advantages n Solving difficult problems n Divide and conquer is a powerful tool for solving conceptually difficult problems, all it requires is a way of breaking the problem into sub-problems, of solving the trivial cases and of combining sub-problems to the original problem. n Algorithm efficiency Moreover, divide and conquer often provides a natural way to design efficient algorithms. n n n Parallelism Divide and conquer algorithms are naturally adapted for execution in multiprocessor machines. Memory access Divide-and-conquer algorithms naturally tend to make efficient use of memory caches. The reason is that once a sub-problem is small enough, it and all its subproblems can, in principle, be solved within the cache, without accessing the slower main memory. 12

Lecture 05. 1 ITS 033 – Programming & Algorithms Divide & Conquer: Mergesort Asst. Prof. Dr. Bunyarit Uyyanonvara IT Program, Image and Vision Computing Lab. School of Information and Computer Technology Sirindhorn International Institute of Technology Thammasat University http: //www. siit. tu. ac. th/bunyarit@siit. tu. ac. th 02 5013505 X 2005 13

Introduction n Sorting is the process of arranging a list of items into a particular order n There must be some values on which the order is based n There are many algorithms for sorting a list of items n These algorithms vary in efficiency 14

Introduction n Selection Sort => O(n 2) n Bubble Sort => O(n 2) 15

Introduction n if n=100, both of the above algorithms run approximately 100 x 100 = 10, 000 comparison n However, if the input is divided to two N 2/4 of (n/2)=50, then the total running time would be approximately n = (n/2)2 + (n/2)2 = N 2/4 + N 2/4 = 2 (N 2/4) = N 2/2 n n n 16

Merge Sort the algorithm • The strategy behind Merge Sort is to change the problem of sorting into the problem of merging two sorted sub-lists into one. • If the two halves of the array were sorted, then merging them carefully could complete the sort of the entire list. 17

Merge-Sort n Merge-sort on an input sequence S with n elements consists of three steps: ¨ Divide: n partition S into two sequences S 1 and S 2 of about n/2 elements each ¨ Recur: n recursively sort S 1 and S 2 ¨ Conquer: n merge S 1 and S 2 into a unique sorted sequence 18

Merge-Sort Algorithm merge. Sort(S, C) Input sequence S with n elements Output sequence S sorted if size of S > 1 (S 1, S 2) partition(S, n/2) merge. Sort(S 1) merge. Sort(S 2) S merge(S 1, S 2) 19

4 Merge Sort the algorithm • Merge Sort is a "recursive" algorithm because it accomplishes its task by calling itself on a smaller version of the problem (only half of the list). • For example, if the array had 2 entries, Merge Sort would begin by calling itself for item 1. Since there is only one element, that sub-list is sorted and it can go on to call itself in item 2. • Since that also has only one item, it is sorted and now Merge Sort can merge those two sub-lists into one sorted list of size two. 20

Merging Two Sorted Sequences Algorithm merge(A, B) //Merges A and B, two sorted arrays into one sorted array, S Input sequences A and B Output sorted sequence of A B S empty sequence while A is not Empty and B is not Empty if A[current] < B. [current] Copy current elemet of A to S Move A to the next element else Copy current elemet of B to S Move B to the next element If A is still not Empty then If B is still not Empty then return S copy all of A to S copy all of B to S 21

4 Merge Sort the algorithm n The real problem is how to merge the two sub-lists. n While it can be done in the original array, the algorithm is much simpler if it uses a separate array to hold the portion that has been merged and then copies the merged data back into the original array. n The basic philosophy of the merge is to determine which sub-list starts with the smallest data and copy that item into the merged list and move on to the next item in the sub-list. 22

Merging Two Sorted Sequences n The conquer step of merge-sort consists of merging two sorted sequences A and B into a sorted sequence S containing the union of the elements of A and B n Merging two sorted sequences, each with n/2 elements and implemented by means of a doubly linked list, (a special data structure) takes O(n) time 23

Merge-Sort Tree n An execution of merge-sort is depicted by a binary tree ¨ each node represents a recursive call of merge-sort and stores n unsorted sequence before the execution and its partition n sorted sequence at the end of the execution ¨ the root is the initial call ¨ the leaves are calls on subsequences of size 0 or 1 7 2 7 9 4 2 4 7 9 2 2 7 7 7 2 2 9 4 4 9 9 9 4 4 24

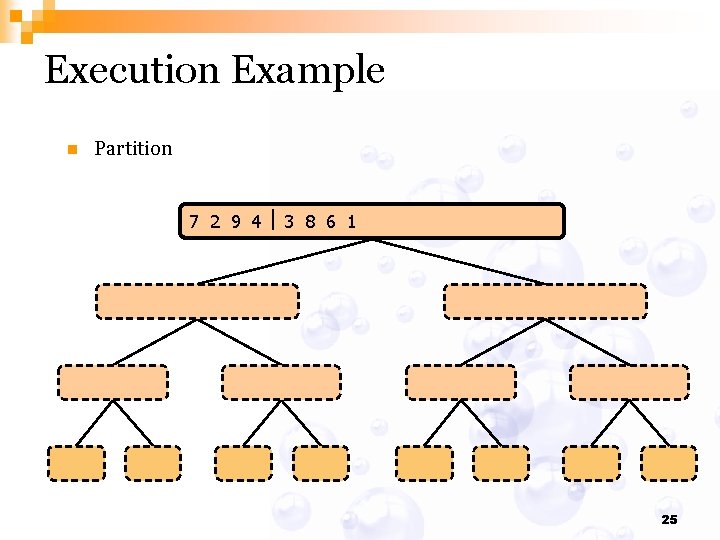
Execution Example n Partition 7 2 9 4 3 8 6 1 1 2 3 4 6 7 8 9 7 2 9 4 2 4 7 9 7 2 2 7 7 7 2 2 3 8 6 1 1 3 8 6 9 4 4 9 9 9 4 4 3 8 3 3 8 8 6 1 1 6 6 6 1 1 25

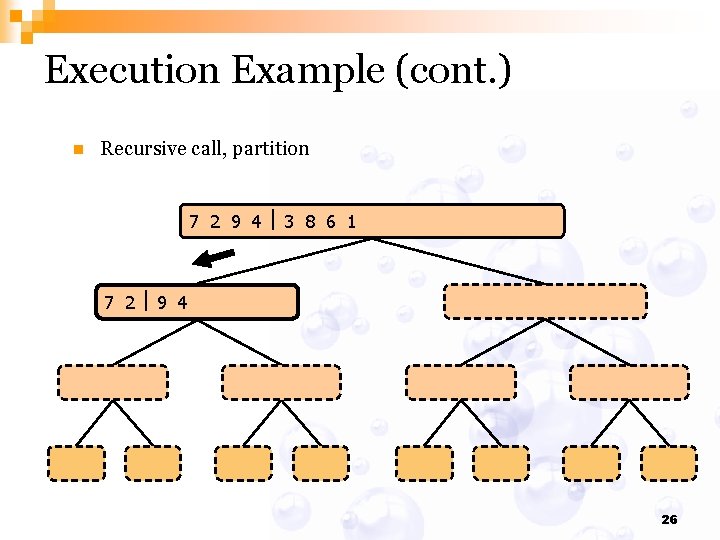
Execution Example (cont. ) n Recursive call, partition 7 2 9 4 3 8 6 1 1 2 3 4 6 7 8 9 7 2 9 4 2 4 7 9 7 2 2 7 7 7 2 2 3 8 6 1 1 3 8 6 9 4 4 9 9 9 4 4 3 8 3 3 8 8 6 1 1 6 6 6 1 1 26

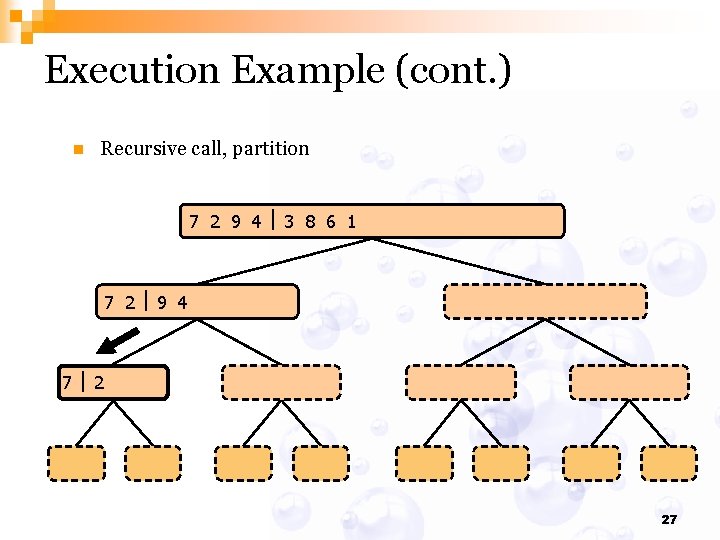
Execution Example (cont. ) n Recursive call, partition 7 2 9 4 3 8 6 1 1 2 3 4 6 7 8 9 7 2 9 4 2 4 7 9 7 2 2 7 7 7 2 2 3 8 6 1 1 3 8 6 9 4 4 9 9 9 4 4 3 8 3 3 8 8 6 1 1 6 6 6 1 1 27

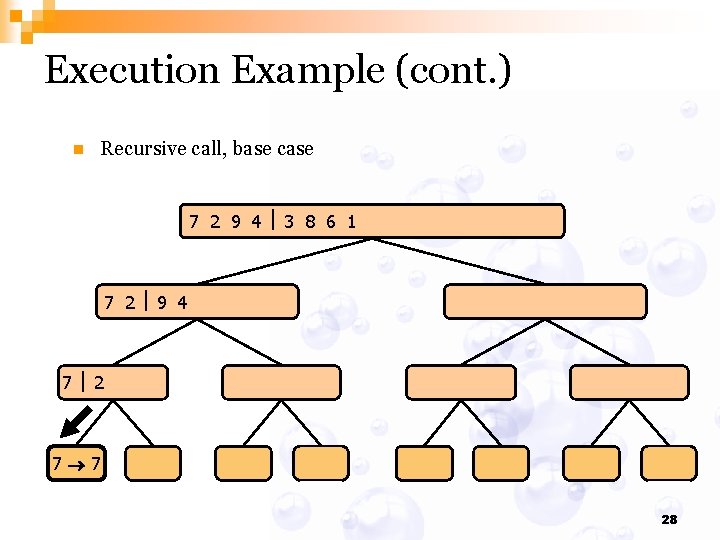
Execution Example (cont. ) n Recursive call, base case 7 2 9 4 3 8 6 1 1 2 3 4 6 7 8 9 7 2 9 4 2 4 7 9 7 2 2 7 7 7 2 2 3 8 6 1 1 3 8 6 9 4 4 9 9 9 4 4 3 8 3 3 8 8 6 1 1 6 6 6 1 1 28

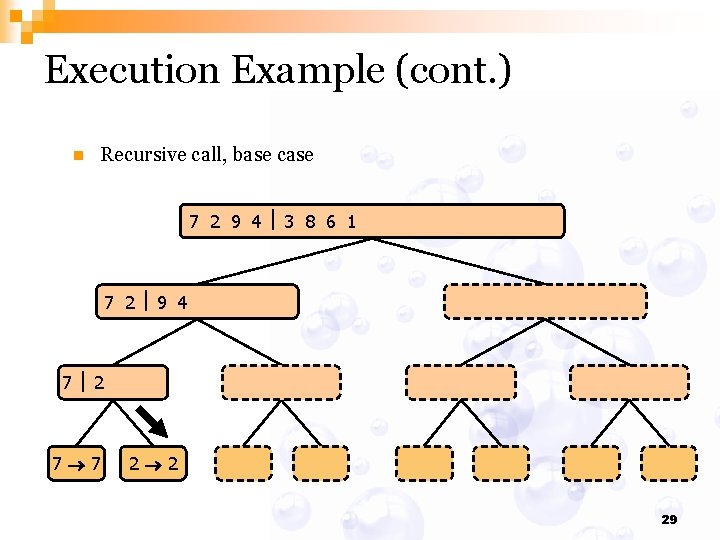
Execution Example (cont. ) n Recursive call, base case 7 2 9 4 3 8 6 1 1 2 3 4 6 7 8 9 7 2 9 4 2 4 7 9 7 2 2 7 7 7 2 2 3 8 6 1 1 3 8 6 9 4 4 9 9 9 4 4 3 8 3 3 8 8 6 1 1 6 6 6 1 1 29

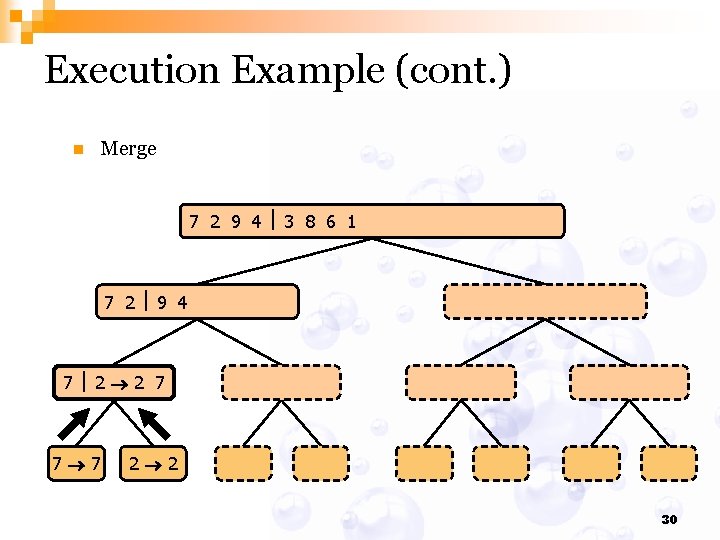
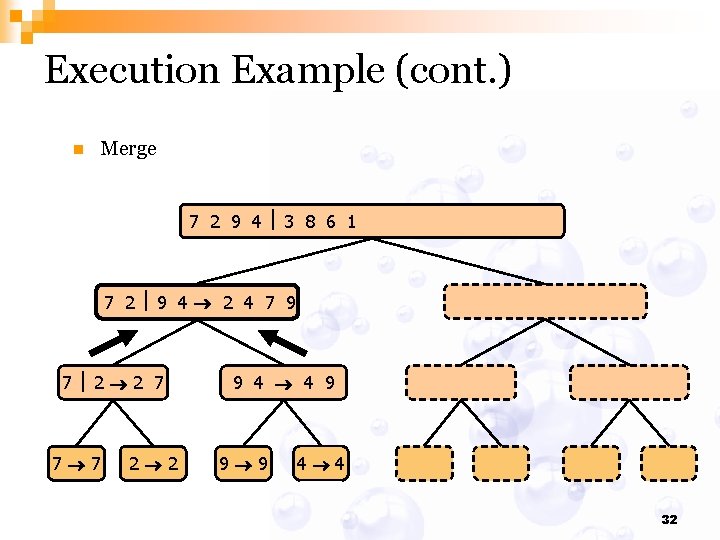
Execution Example (cont. ) n Merge 7 2 9 4 3 8 6 1 1 2 3 4 6 7 8 9 7 2 9 4 2 4 7 9 7 2 2 7 7 7 2 2 3 8 6 1 1 3 8 6 9 4 4 9 9 9 4 4 3 8 3 3 8 8 6 1 1 6 6 6 1 1 30

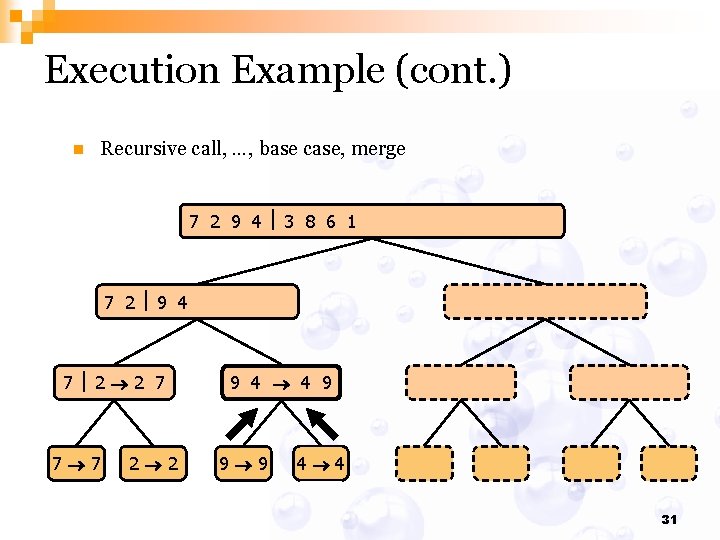
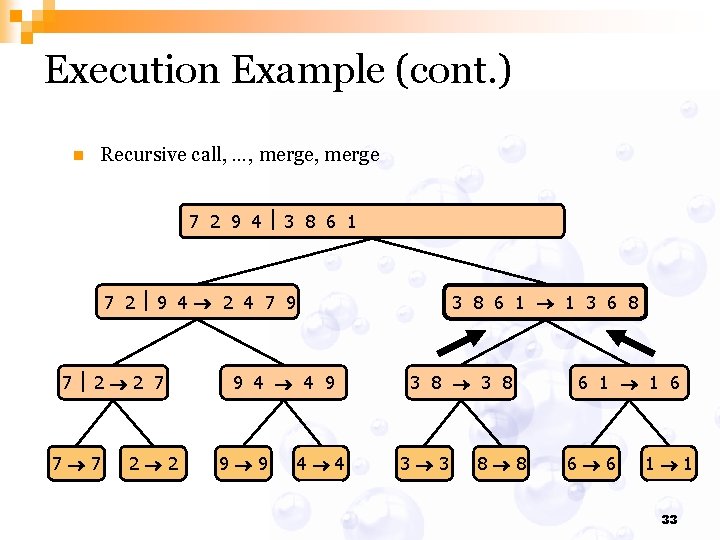
Execution Example (cont. ) n Recursive call, …, base case, merge 7 2 9 4 3 8 6 1 1 2 3 4 6 7 8 9 7 2 9 4 2 4 7 9 7 2 2 7 7 7 2 2 3 8 6 1 1 3 8 6 9 4 4 9 9 9 4 4 3 8 3 3 8 8 6 1 1 6 6 6 1 1 31

Execution Example (cont. ) n Merge 7 2 9 4 3 8 6 1 1 2 3 4 6 7 8 9 7 2 9 4 2 4 7 9 7 2 2 7 7 7 2 2 3 8 6 1 1 3 8 6 9 4 4 9 9 9 4 4 3 8 3 3 8 8 6 1 1 6 6 6 1 1 32

Execution Example (cont. ) n Recursive call, …, merge 7 2 9 4 3 8 6 1 1 2 3 4 6 7 8 9 7 2 9 4 2 4 7 9 7 2 2 7 7 7 2 2 3 8 6 1 1 3 6 8 9 4 4 9 9 9 4 4 3 8 3 3 8 8 6 1 1 6 6 6 1 1 33

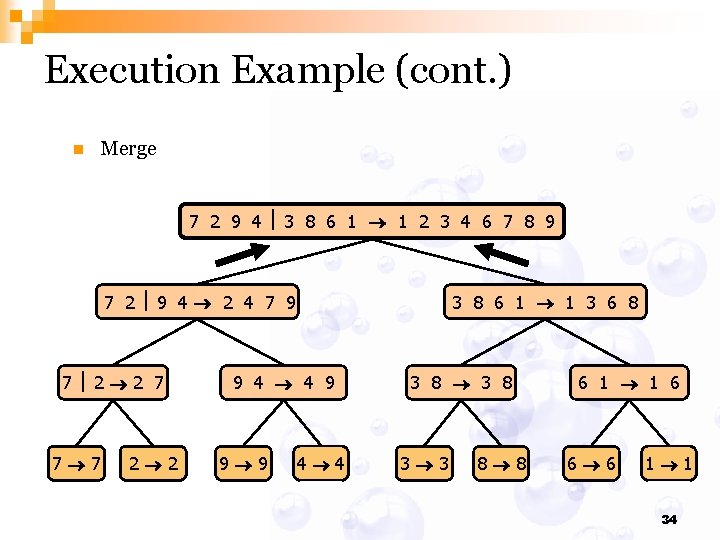
Execution Example (cont. ) n Merge 7 2 9 4 3 8 6 1 1 2 3 4 6 7 8 9 7 2 9 4 2 4 7 9 7 2 2 7 7 7 2 2 3 8 6 1 1 3 6 8 9 4 4 9 9 9 4 4 3 8 3 3 8 8 6 1 1 6 6 6 1 1 34

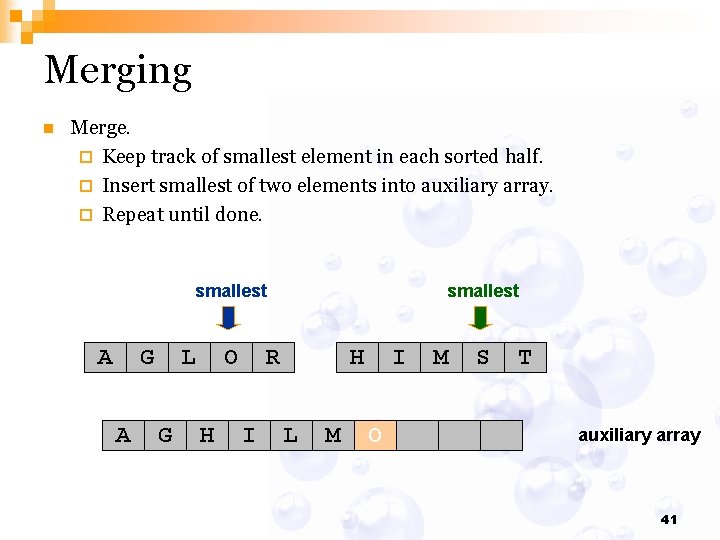
Merging n Merge. ¨ Keep track of smallest element in each sorted half. ¨ Insert smallest of two elements into auxiliary array. ¨ Repeat until done. smallest A G A smallest L O R H I M S T auxiliary array 35

Merging n Merge. ¨ Keep track of smallest element in each sorted half. ¨ Insert smallest of two elements into auxiliary array. ¨ Repeat until done. smallest A G A L G smallest O R H I M S T auxiliary array 36

Merging n Merge. ¨ Keep track of smallest element in each sorted half. ¨ Insert smallest of two elements into auxiliary array. ¨ Repeat until done. smallest A G A L G O H smallest R H I M S T auxiliary array 37

Merging n Merge. ¨ Keep track of smallest element in each sorted half. ¨ Insert smallest of two elements into auxiliary array. ¨ Repeat until done. smallest A G A L G smallest O H R I H I M S T auxiliary array 38

Merging n Merge. ¨ Keep track of smallest element in each sorted half. ¨ Insert smallest of two elements into auxiliary array. ¨ Repeat until done. smallest A G A L G smallest O H R I H L I M S T auxiliary array 39

Merging n Merge. ¨ Keep track of smallest element in each sorted half. ¨ Insert smallest of two elements into auxiliary array. ¨ Repeat until done. smallest A G A L G O H smallest R I H L M I M S T auxiliary array 40

Merging n Merge. ¨ Keep track of smallest element in each sorted half. ¨ Insert smallest of two elements into auxiliary array. ¨ Repeat until done. smallest A G A L G O H smallest R I H L M I O M S T auxiliary array 41

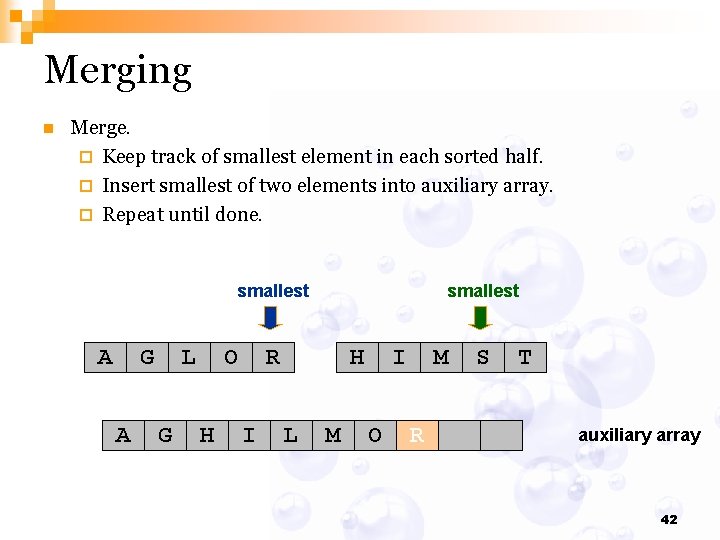
Merging n Merge. ¨ Keep track of smallest element in each sorted half. ¨ Insert smallest of two elements into auxiliary array. ¨ Repeat until done. smallest A G A L G O H smallest R I H L M I O M R S T auxiliary array 42

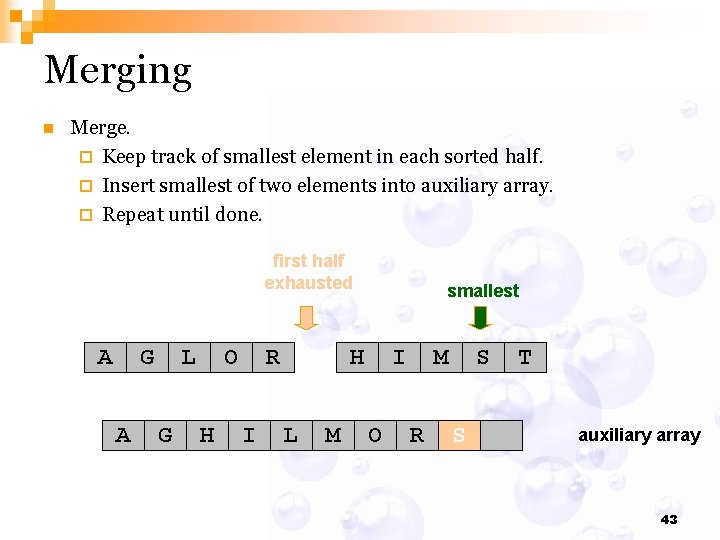
Merging n Merge. ¨ Keep track of smallest element in each sorted half. ¨ Insert smallest of two elements into auxiliary array. ¨ Repeat until done. first half exhausted A G A L G O H R I smallest H L M I O M R S S T auxiliary array 43

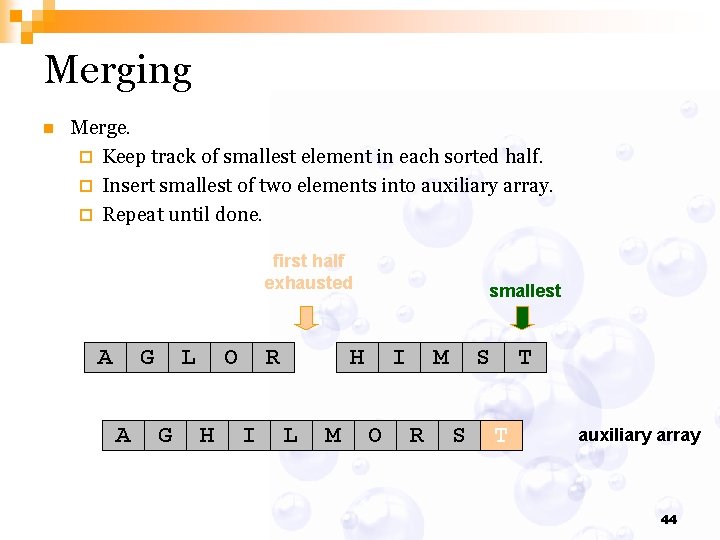
Merging n Merge. ¨ Keep track of smallest element in each sorted half. ¨ Insert smallest of two elements into auxiliary array. ¨ Repeat until done. first half exhausted A G A L G O H R I smallest H L M I O M R S S T T auxiliary array 44

Merging n Merge. ¨ Keep track of smallest element in each sorted half. ¨ Insert smallest of two elements into auxiliary array. ¨ Repeat until done. first half exhausted A G A L G O H R I second half exhausted H L M I O M R S S T T auxiliary array 45

Analysis of Merge-Sort n n n The height h of the merge-sort tree is O(log n) ¨ at each recursive call we divide in half the sequence, The overall amount or work done at the nodes of depth i is O(n) ¨ we partition and merge 2 i sequences of size n/2 i ¨ we make 2 i+1 recursive calls Thus, the total running time of merge-sort is O(n log n) depth #seqs size 0 1 n 1 2 n/2 i 2 i n/2 i … … … 46

Merge Sort the analysis • Merge. Sort is a classic example of the techniques used to analyze recursive routines: • Merge Sort is a divide-and-conquer recursive algorithm. • Merge. Sort’s running time is O(N log N). 47

Merge Sort the analysis • Although its running time is O(N log N), it is hardly ever used for the main memory sorts that’s because it consumes a lot of memory. • The main problem is that merging two sorted lists requires linear extra memory, and the additional work spent copying to the temporary array and back throughout the algorithm. • Which effect in slowing down the sort. n The principal shortcoming of mergesort is the linear amount of extra storage the algorithm requires. n Though merging can be done in place, the resulting algorithm is quite complicated and, since it has a significantly larger multiplicative constant, the in-place mergesort is of theoretical interest only. 48

Lecture 05. 2 ITS 033 – Programming & Algorithms Divide & Conquer: Quicksort Asst. Prof. Dr. Bunyarit Uyyanonvara IT Program, Image and Vision Computing Lab. School of Information and Computer Technology Sirindhorn International Institute of Technology Thammasat University http: //www. siit. tu. ac. th/bunyarit@siit. tu. ac. th 02 5013505 X 2005 49

Quick Sort the algorithm • Quick Sort's approach is to take Merge Sort's philosophy but eliminate the need for the merging steps. • Can you see how the problem could be solved ? 50

Quick Sort the algorithm • It makes sure that every data item in the first sub-list is less than every data item in the second sub-list. • The procedure that accomplished that is called "partitioning" the data. After the paritioning, , each of the sub-lists are sorted, which will cause the entire array to be sorted. 51

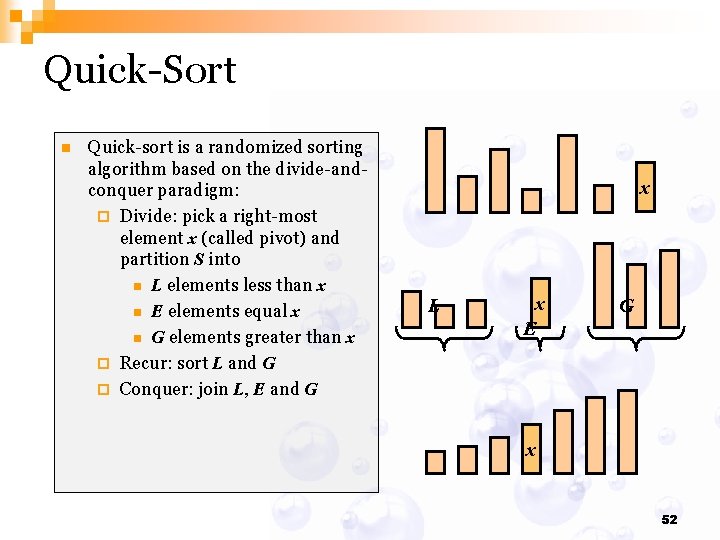
Quick-Sort n Quick-sort is a randomized sorting algorithm based on the divide-andconquer paradigm: ¨ Divide: pick a right-most element x (called pivot) and partition S into n L elements less than x n E elements equal x n G elements greater than x ¨ Recur: sort L and G ¨ Conquer: join L, E and G x L x E G x 52

Quick Sort n Quick sort divides the inputs according to their value to achieve its partition: Pivot n Then it partition the inputs to partition that have greater value than pivot, and partition that have smaller value than pivot. 53

Quick Sort ALGORITHM Quicksort(A[l. . r]) //Sorts a subarray by quicksort //Input: A subarray A[l. . r] of A[0. . n - 1], defined by its left // and right indices l and r //Output: The subarray A[l. . r] sorted in nondecreasing order if l < r s Partition(A[l. . r]) //s is a split position Quicksort(A[l. . s - 1]) Quicksort(A[s + 1. . r]) 54

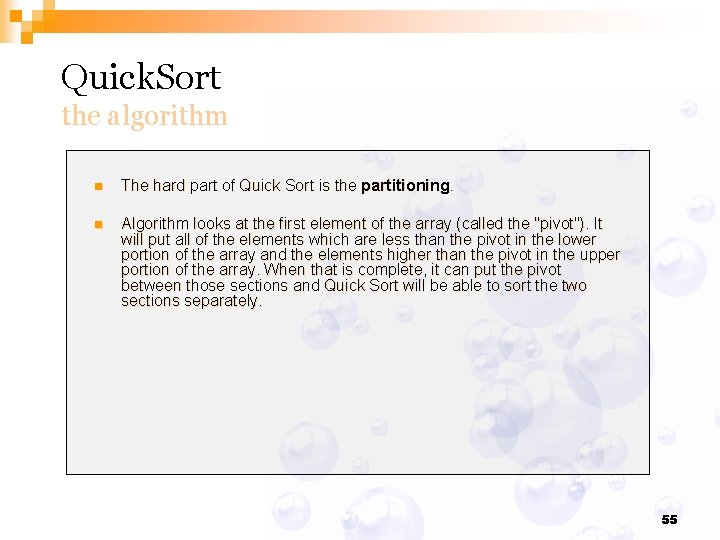
Quick. Sort the algorithm n The hard part of Quick Sort is the partitioning. n Algorithm looks at the first element of the array (called the "pivot"). It will put all of the elements which are less than the pivot in the lower portion of the array and the elements higher than the pivot in the upper portion of the array. When that is complete, it can put the pivot between those sections and Quick Sort will be able to sort the two sections separately. 55

Partition n We partition an input sequence as follows: ¨ We remove, in turn, each element y from S and ¨ We insert y into L, E or G, depending on the result of the comparison with the pivot x Each insertion and removal is at the beginning or at the end of a sequence, and hence takes O(1) time Thus, the partition step of quick-sort takes O(n) time 56

Partition Procedure ALGORITHM Partition(A[l. . r]) //Partitions subarray by using its first element as a pivot //Input: subarray A[l. . r] of A[0. . n - 1], defined by its left and right indices l and r (l< r) //Output: A partition of A[l. . r], with the split position returned as this function’s value p A[l] i . l; j r + 1 repeat i . i + 1 until A[i] ≥ p repeat j. j 1 until A[j ] ≤ p swap(A[i], A[j ]) until i ≥ j swap(A[i], A[j ]) //undo last swap when i ≥ j swap(A[l], A[j ]) return j 57

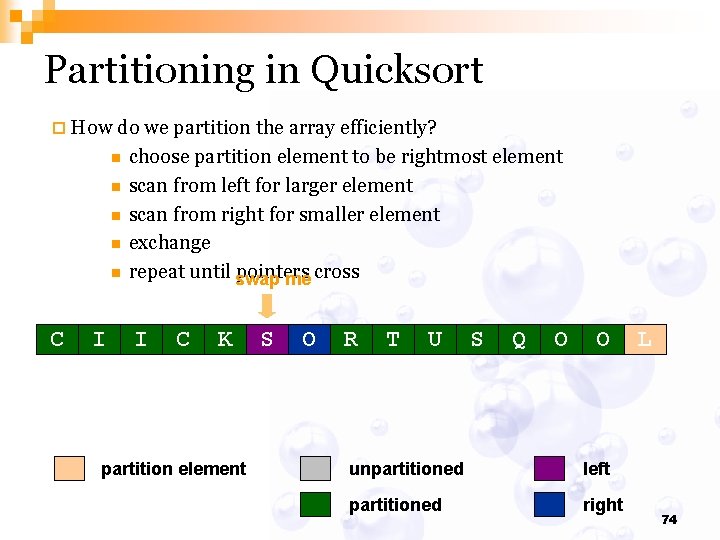
Partitioning in Quicksort ¨ How do we partition the array efficiently? n n n Q U choose partition element to be rightmost element scan from left for larger element scan from right for smaller element exchange repeat until pointers cross I C K partition element S O R T I S C O O unpartitioned left partitioned right L 58

Partitioning in Quicksort ¨ How do we partition the array efficiently? n n n swap me Q U choose partition element to be rightmost element scan from left for larger element scan from right for smaller element exchange repeat until pointers cross I C K partition element S O R T I S C O O unpartitioned left partitioned right L 59

Partitioning in Quicksort ¨ How do we partition the array efficiently? n n n swap me Q U choose partition element to be rightmost element scan from left for larger element scan from right for smaller element exchange repeat until pointers cross I C K partition element S O R T I S C O O unpartitioned left partitioned right L 60

Partitioning in Quicksort ¨ How do we partition the array efficiently? n n n swap me Q U choose partition element to be rightmost element scan from left for larger element scan from right for smaller element exchange repeat until pointers cross I C K partition element S O R T I S C O O unpartitioned left partitioned right L 61

Partitioning in Quicksort ¨ How do we partition the array efficiently? n n n swap me Q U choose partition element to be rightmost element scan from left for larger element scan from right for smaller element exchange repeat until pointers cross swap me I C K partition element S O R T I S C O O unpartitioned left partitioned right L 62

Partitioning in Quicksort ¨ How do we partition the array efficiently? n n n C U choose partition element to be rightmost element scan from left for larger element scan from right for smaller element exchange repeat until pointers cross I C K partition element S O R T I S Q O O unpartitioned left partitioned right L 63

Partitioning in Quicksort ¨ How do we partition the array efficiently? choose partition element to be rightmost element n scan from left for larger element n scan from right for smaller element n exchange repeat until pointers cross swapnme n C U I C K partition element S O R T I S Q O O unpartitioned left partitioned right L 64

Partitioning in Quicksort ¨ How do we partition the array efficiently? choose partition element to be rightmost element n scan from left for larger element n scan from right for smaller element n exchange repeat until pointers cross swapnme n C U I C K partition element S O R T I S Q O O unpartitioned left partitioned right L 65

Partitioning in Quicksort ¨ How do we partition the array efficiently? choose partition element to be rightmost element n scan from left for larger element n scan from right for smaller element n exchange repeat until pointers cross swapnme swap me n C U I C K partition element S O R T I S Q O O unpartitioned left partitioned right L 66

Partitioning in Quicksort ¨ How do we partition the array efficiently? n n n C I choose partition element to be rightmost element scan from left for larger element scan from right for smaller element exchange repeat until pointers cross I C K partition element S O R T U S Q O O unpartitioned left partitioned right L 67

Partitioning in Quicksort ¨ How do we partition the array efficiently? n n n C I choose partition element to be rightmost element scan from left for larger element scan from right for smaller element exchange repeat until pointers cross I C K partition element S O R T U S Q O O unpartitioned left partitioned right L 68

Partitioning in Quicksort ¨ How do we partition the array efficiently? n n n C I choose partition element to be rightmost element scan from left for larger element scan from right for smaller element exchange repeat until pointers cross I C K partition element S O R T U S Q O O unpartitioned left partitioned right L 69

Partitioning in Quicksort ¨ How do we partition the array efficiently? n n n C I choose partition element to be rightmost element scan from left for larger element scan from right for smaller element exchange repeat until pointers cross I C K partition element S O R T U S Q O O unpartitioned left partitioned right L 70

Partitioning in Quicksort ¨ How do we partition the array efficiently? n n n C I choose partition element to be rightmost element scan from left for larger element scan from right for smaller element exchange repeat until swap pointers me cross I C K partition element S O R T U S Q O O unpartitioned left partitioned right L 71

Partitioning in Quicksort ¨ How do we partition the array efficiently? n n n C I choose partition element to be rightmost element scan from left for larger element scan from right for smaller element exchange repeat until swap pointers me cross I C K partition element S O R T U S Q O O unpartitioned left partitioned right L 72

Partitioning in Quicksort ¨ How do we partition the array efficiently? n n n C I choose partition element to be rightmost element scan from left for larger element scan from right for smaller element exchange repeat until swap pointers me cross I C K partition element S O R T U S Q O O unpartitioned left partitioned right L 73

Partitioning in Quicksort ¨ How do we partition the array efficiently? n n n C I choose partition element to be rightmost element scan from left for larger element scan from right for smaller element exchange repeat until swap pointers me cross I C K partition element S O R T U S Q O O unpartitioned left partitioned right L 74

Partitioning in Quicksort ¨ How do we partition the array efficiently? n n n choose partition element to be rightmost element scan from left for larger element scan from right for smaller element exchange swap with repeat until pointers cross partitioning element C I I C K partition element S O R T U S Q O O unpartitioned left partitioned right L 75

Partitioning in Quicksort ¨ How do we partition the array efficiently? n n n C I choose partition element to be rightmost element scan from left for larger element scan from right for smaller element exchange partition is repeat until pointers cross complete I C K partition element L O R T U S Q O O unpartitioned left partitioned right S 76

Quick Sort the analysis • Like Merge Sort, Quick. Sort is a divide-and-conquer recursive algorithm. • Quick. Sort is the fastest known sorting algorithm in practice. • Its average running time is O(N log N). • However, it has O(N 2) for worst-case performance. n On the average, quicksort makes only 38% more comparisons than in the best case. n Moreover, its innermost loop is so efficient that it runs faster than mergesort 77

Summary of Sorting Algorithms Algorithm Time Notes Bubble-sort O(n 2) n Selection-sort O(n 2) n merge-sort O(n log n) n quick-sort O(n log n) expected n in-place n slow (good for small inputs) sequential data access n fast (good for huge inputs) in-place, randomized n fastest (good for large inputs) 78

Lecture 05. 3 ITS 033 – Programming & Algorithms Divide & Conquer: Binary Search Asst. Prof. Dr. Bunyarit Uyyanonvara IT Program, Image and Vision Computing Lab. School of Information and Computer Technology Sirindhorn International Institute of Technology Thammasat University http: //www. siit. tu. ac. th/bunyarit@siit. tu. ac. th 02 5013505 X 2005 79

Binary search • Binary Search is an incredibly powerful technique for searching an ordered list. • The basic algorithm is to find the middle element of the list, compare it against the key, decide which half of the list must contain the key, and repeat with that half. 80

Binary Search n It works by comparing a search key K with the array’s middle element A[m]. n If they match, the algorithm stops; otherwise, the same operation is repeated recursively for the first half of the array if. K <A[m] and for the second half if. K >A[m]: 81

Binary search Algorithm Binary. Search. On. Sorted Input: an array, a key Output: Location of the key 1. 2. Sort the array (smallest to biggest) start with the middle element of the array If it matches then done If middle element > key then search array’s 1 st half If middle element < key then search array’s 2 nd half 82

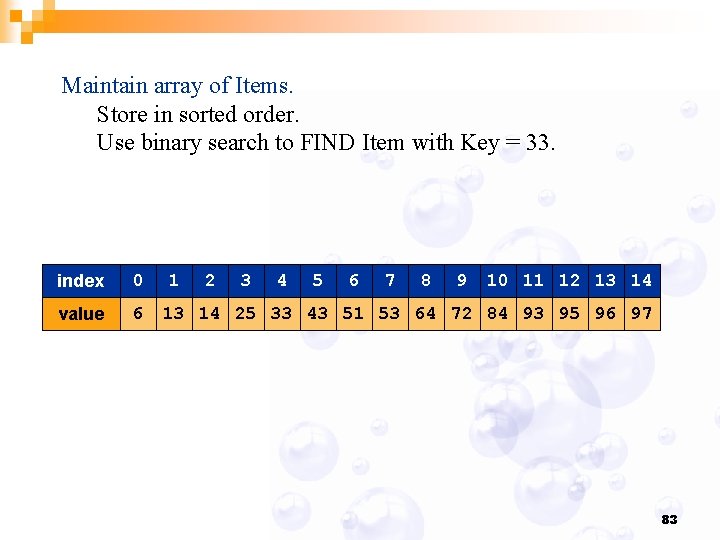
Maintain array of Items. Store in sorted order. Use binary search to FIND Item with Key = 33. index 0 value 6 1 2 3 4 5 6 7 8 9 10 11 12 13 14 25 33 43 51 53 64 72 84 93 95 96 97 83

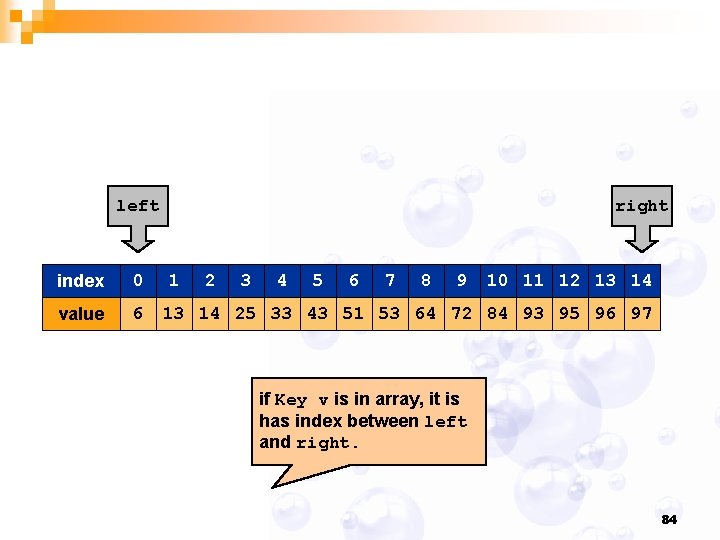
left index 0 value 6 right 1 2 3 4 5 6 7 8 9 10 11 12 13 14 25 33 43 51 53 64 72 84 93 95 96 97 if Key v is in array, it is has index between left and right. 84

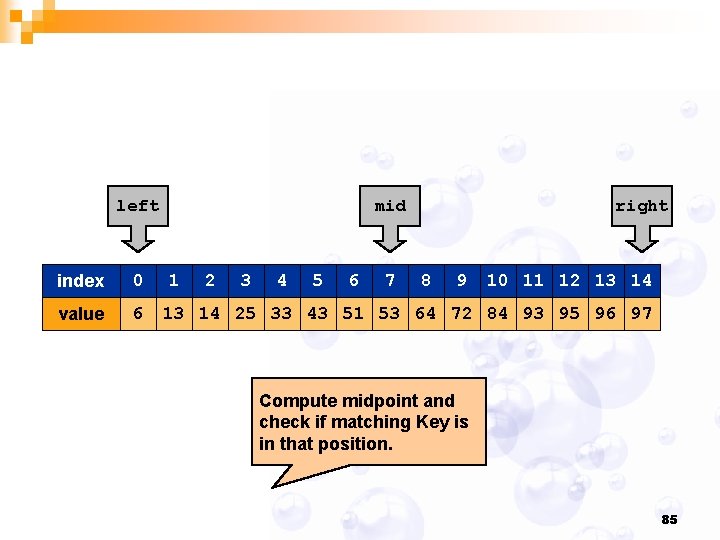
left index 0 value 6 mid 1 2 3 4 5 6 7 right 8 9 10 11 12 13 14 25 33 43 51 53 64 72 84 93 95 96 97 Compute midpoint and check if matching Key is in that position. 85

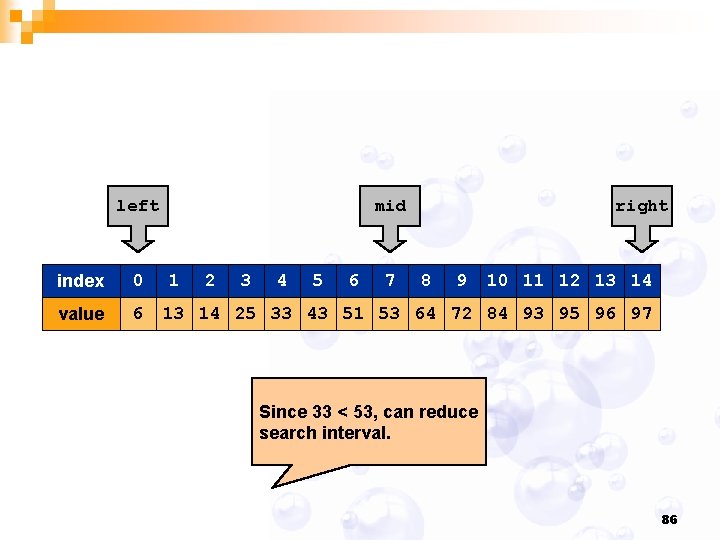
left index 0 value 6 mid 1 2 3 4 5 6 7 right 8 9 10 11 12 13 14 25 33 43 51 53 64 72 84 93 95 96 97 Since 33 < 53, can reduce search interval. 86

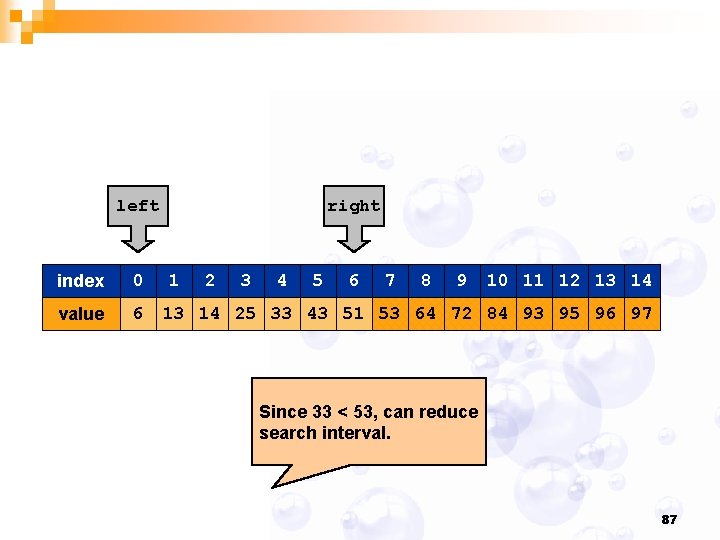
left index 0 value 6 right 1 2 3 4 5 6 7 8 9 10 11 12 13 14 25 33 43 51 53 64 72 84 93 95 96 97 Since 33 < 53, can reduce search interval. 87

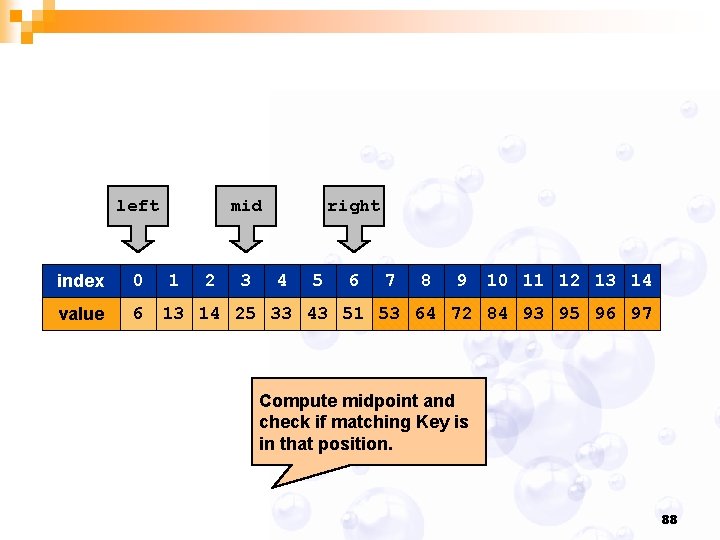
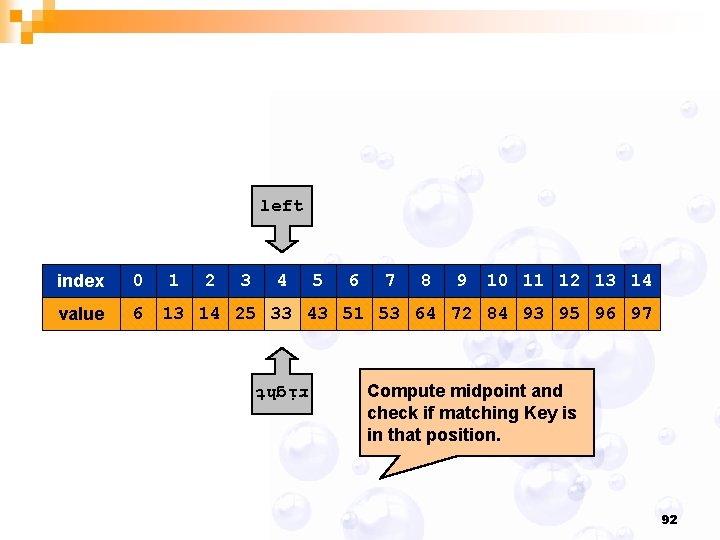
left index 0 value 6 mid 1 2 3 right 4 5 6 7 8 9 10 11 12 13 14 25 33 43 51 53 64 72 84 93 95 96 97 Compute midpoint and check if matching Key is in that position. 88

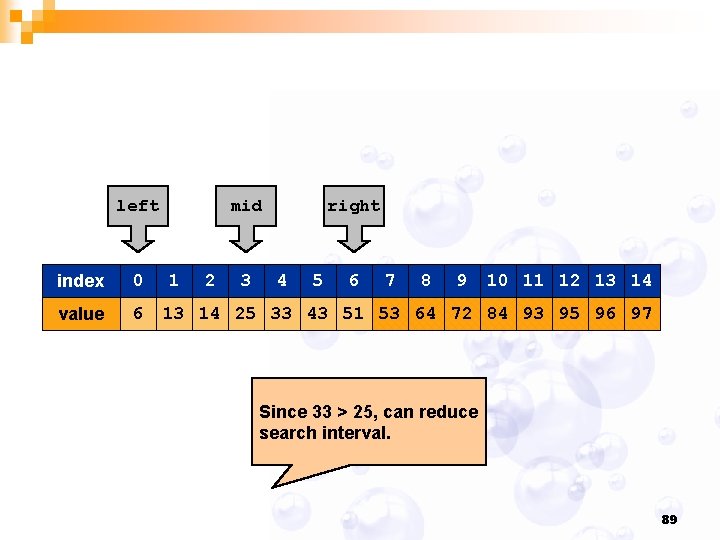
left index 0 value 6 mid 1 2 3 right 4 5 6 7 8 9 10 11 12 13 14 25 33 43 51 53 64 72 84 93 95 96 97 Since 33 > 25, can reduce search interval. 89

left index 0 value 6 1 2 3 4 right 5 6 7 8 9 10 11 12 13 14 25 33 43 51 53 64 72 84 93 95 96 97 Since 33 > 25, can reduce search interval. 90

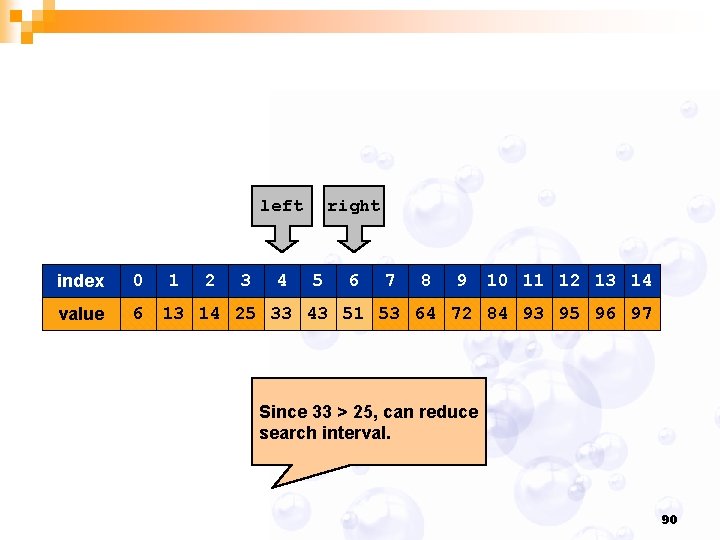
left 0 value 6 1 2 3 4 5 6 7 8 9 10 11 12 13 14 25 33 43 51 53 64 72 84 93 95 96 97 mid index right 91

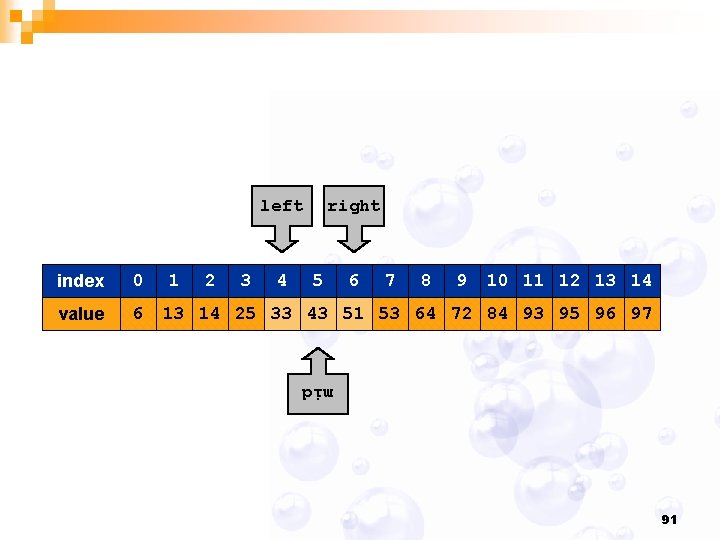
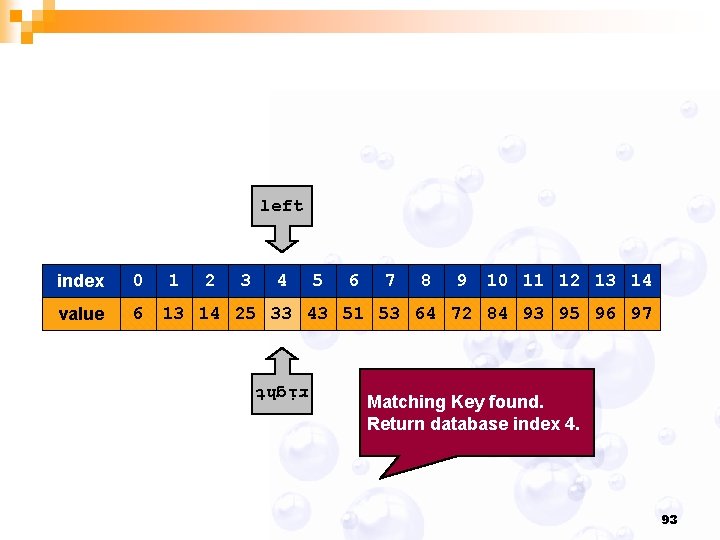
left 0 value 6 1 2 3 4 5 6 7 8 9 10 11 12 13 14 25 33 43 51 53 64 72 84 93 95 96 97 right index Compute midpoint and check if matching Key is in that position. 92

left 0 value 6 1 2 3 4 5 6 7 8 9 10 11 12 13 14 25 33 43 51 53 64 72 84 93 95 96 97 right index Matching Key found. Return database index 4. 93

Binary search Found = false while (not Found) and (Left<=Right) do { Mid = (Left+Right)/2; if Key==Array[Mid] then Found=true; else if Key < Array[Mid] then Right = Mid-1; else if Key > Array[Mid] then Left = Mid+1; } 94

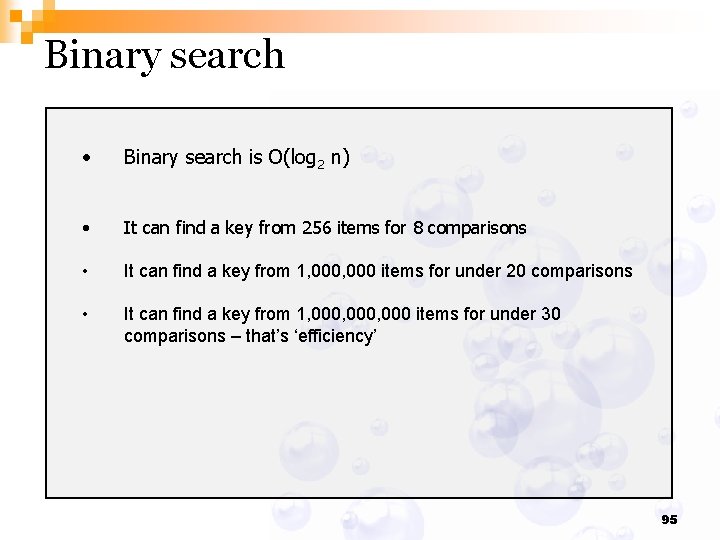
Binary search • Binary search is O(log 2 n) • It can find a key from 256 items for 8 comparisons • It can find a key from 1, 000 items for under 20 comparisons • It can find a key from 1, 000, 000 items for under 30 comparisons – that’s ‘efficiency’ 95

Lecture 05. 4 ITS 033 – Programming & Algorithms Divide & Conquer: Closest Pair Problem Asst. Prof. Dr. Bunyarit Uyyanonvara IT Program, Image and Vision Computing Lab. School of Information and Computer Technology Sirindhorn International Institute of Technology Thammasat University http: //www. siit. tu. ac. th/bunyarit@siit. tu. ac. th 02 5013505 X 2005 96

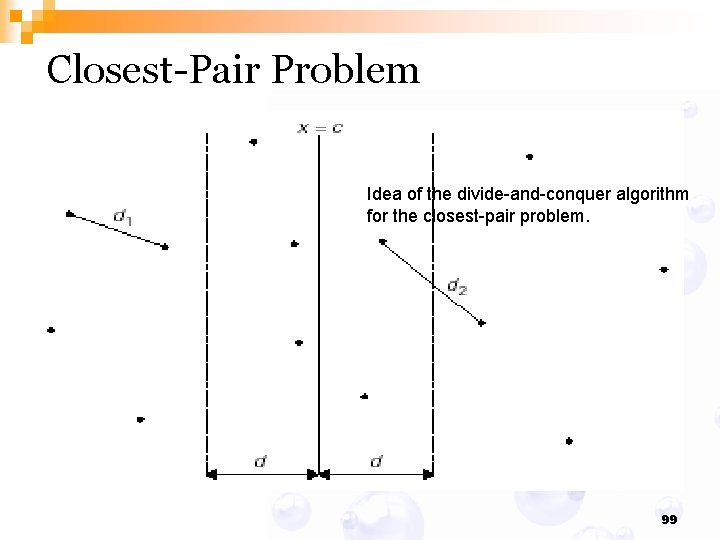
Closest-Pair Problems by Divide-and. Conquer Closest-Pair Problem n Let P 1 = (x 1, y 1), . . . , Pn = (xn, yn) be a set S of n points in the plane, where n, for simplicity, is a power of two. We can divide the points given into two subsets S 1 and S 2 of n/2 points each by drawing a vertical line x = c. n Thus, n/2 points lie to the left of or on the line itself and n/2 points lie to the right of or on the line. 97

Closest-Pair Problem n Following the divide-and-conquer approach, we can find recursively the closest pairs for the left subset S 1 and the right subset S 2. Let d 1 and d 2 be the smallest distances between pairs of points in S 1 and S 2, respectively, and let d = min{d 1, d 2}. n Unfortunately, d is not necessarily the smallest distance between all pairs of points in S 1 and S 2 because a closer pair of points can lie on the opposite sides of the separating line. So, as a step of combining the solutions to the smaller subproblems, we need to examine such points. 98

Closest-Pair Problem Idea of the divide-and-conquer algorithm for the closest-pair problem. 99

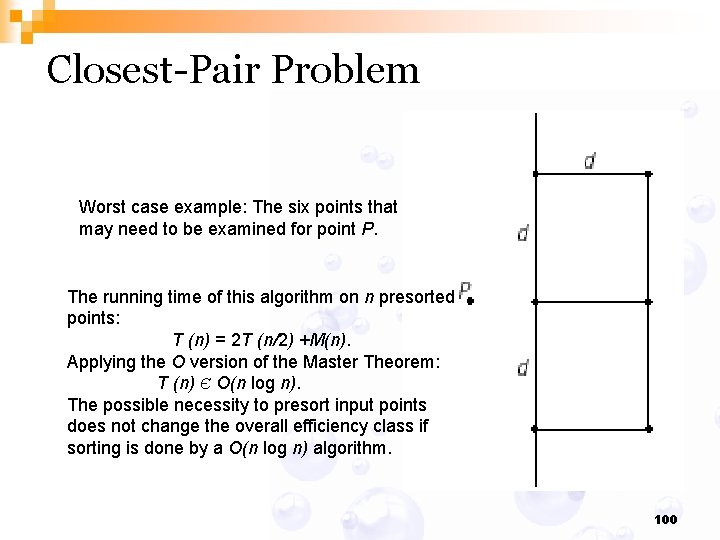
Closest-Pair Problem Worst case example: The six points that may need to be examined for point P. The running time of this algorithm on n presorted points: T (n) = 2 T (n/2) +M(n). Applying the O version of the Master Theorem: T (n) Є O(n log n). The possible necessity to presort input points does not change the overall efficiency class if sorting is done by a O(n log n) algorithm. 100

ITS 033 Topic 01 - Problems & Algorithmic Problem Solving Topic 02 – Algorithm Representation & Efficiency Analysis Topic 03 - State Space of a problem Topic 04 - Brute Force Algorithm Topic 05 - Divide and Conquer Topic 06 - Decrease and Conquer Topic 07 - Dynamics Programming Topic 08 - Transform and Conquer Topic 09 - Graph Algorithms Topic 10 - Minimum Spanning Tree Topic 11 - Shortest Path Problem Topic 12 - Coping with the Limitations of Algorithms Power http: //www. siit. tu. ac. th/bunyarit/its 033. php and http: //www. vcharkarn. com/vlesson/showlesson. php? lessonid=7 101

End of Chapter 4 Thank you! 102