Divideandconquer algorithms Counting inversions Input A permutation a




- Slides: 7

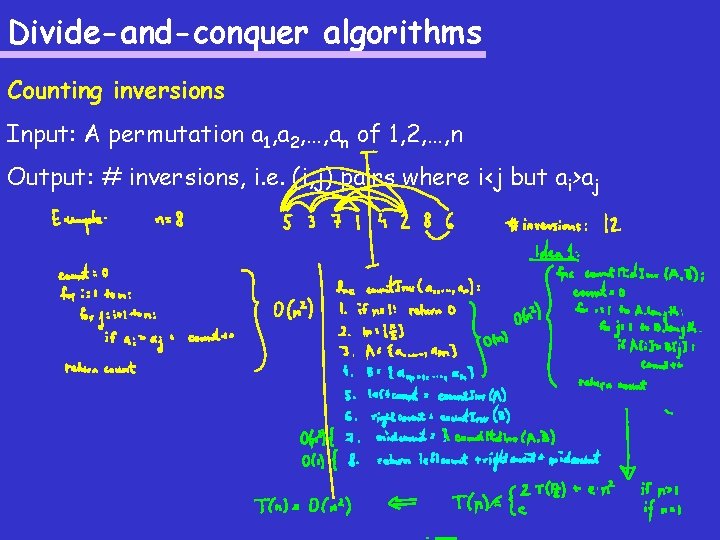
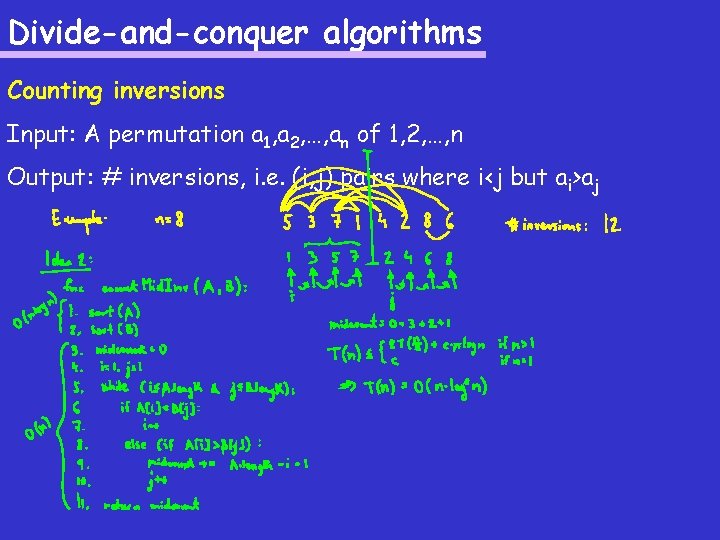
Divide-and-conquer algorithms Counting inversions Input: A permutation a 1, a 2, …, an of 1, 2, …, n Output: # inversions, i. e. (i, j) pairs where i<j but ai>aj

Divide-and-conquer algorithms Counting inversions Input: A permutation a 1, a 2, …, an of 1, 2, …, n Output: # inversions, i. e. (i, j) pairs where i<j but ai>aj

Divide-and-conquer algorithms Counting inversions Input: A permutation a 1, a 2, …, an of 1, 2, …, n Output: # inversions, i. e. (i, j) pairs where i<j but ai>aj

Divide-and-conquer algorithms Closest Pair of Points Input: n points in the plane (x 1, y 1), …, (xn, yn) Output: distance of the closest pair of points, i. e. , mini, j (i j) distance of (xi, yi) and (xj, yj)

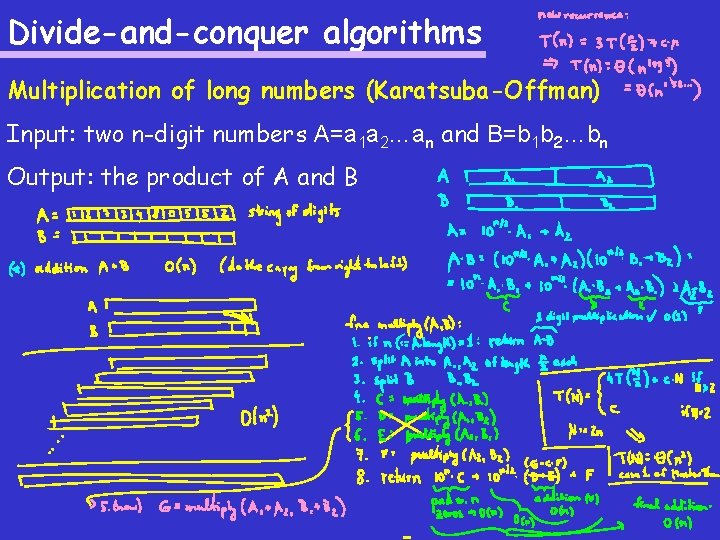
Divide-and-conquer algorithms Multiplication of long numbers (Karatsuba-Offman) Input: two n-digit numbers A=a 1 a 2…an and B=b 1 b 2…bn Output: the product of A and B

Master Theorem Let a ¸ 1 and b>1 be constants, f(n) be a function and for positive integers we have a recurrence for T of the form T(n) = a T(n/b) + f(n), where n/b is rounded either way. Then, • If f(n) = O(nlog a/log b - ) for some constant > 0, then T(n) = (nlog a/log b). • If f(n) = (nlog a/log b), then T(n) = (nlog a/log blog n). • If f(n) = (nlog a/log b + ) for some constant > 0, and if af(n/b) · cf(n) for some constant c < 1 (and all sufficiently large n), then T(n) = (f(n)).

Master Theorem Let a ¸ 1 and b>1 be constants, f(n) be a function and for positive integers we have a recurrence for T of the form T(n) = a T(n/b) + f(n), where n/b is rounded either way. Then, • If f(n) = O(nlog a/log b - ) for some constant > 0, then T(n) = (nlog a/log b). • If f(n) = (nlog a/log b), then T(n) = (nlog a/log blog n). • If f(n) = (nlog a/log b + ) for some constant > 0, and if af(n/b) · cf(n) for some constant c < 1 (and all sufficiently large n), then T(n) = (f(n)).