7 3 DivideandConquer Algorithms and Recurrence Relations If

7. 3 Divide-and-Conquer Algorithms and Recurrence Relations • If f(n) represents the number of operations required to solve the problem of size n, it follow that f satisfies the recurrence relation f(n) = af(n/b) + g(n) this is called a divide-and-conquer algorithms and recurrence relations • Example 1: Binary Search We introduced a binary search algorithm in section 3. 1. 1

The binary search • Algorithm 3: the binary search algorithm Procedure binary search (x: integer, a 1, a 2, …, an: increasing integers) i : =1 { i is left endpoint of search interval} j : =n { j is right endpoint of search interval} While i < j begin m : = (i + j) / 2 if x > am then i : = m+1 else j : = m end If x = ai then location : = i else location : =0 {location is the subscript of the term equal to x, or 0 if x is not found} 2

Divide-and-Conquer Algorithms and Recurrence Relations • Example 3: Merge Sort • Algorithm 9 A Recursive Merge Sort. Procedure mergesort(L = a 1, . . . , an) If n > 1 then m : = n/ 2 L 1 : = a 1, a 2, . . . , am L 2 : = am+1, am+2, . . . , an L : = merge (mergesort(L 1), mergesort(L 2)) {L is now sorted into elements in nondecreasing order} 3

Divide-and-Conquer Algorithms and Recurrence Relations • Example 4: Fast Multiplication of Integers • There are more efficient algorithms than the conventional algorithm (described in section 3. 6) for multiplying integers. • Suppose that a and b are integers with binary expansions of length 2 n. • Let a = (a 2 n-1 a 2 n-2. . . a 1 a 0)2 , b = (a 2 n-1 a 2 n-2. . . a 1 a 0)2 • Let a = 2 n. A 1 + A 0 , b = 2 n. B 1 + B 0 A 1= (a 2 n-1. . . an+1 an)2 , A 0= (an-1. . . a 1 a 0)2, B 1 = (b 2 n-1. . . bn+1 bn)2 , B 0= (bn-1. . . b 1 b 0)2 , • the algorithm for fast multiplication of integers is based on the fact that ab can be rewritten as • ab= (22 n+2 n) A 1 B 1 + 2 n(A 1 - A 0) (B 0 - B 1 ) +(2 n +1)A 0 B 0. 4

Divide-and-Conquer Algorithms and Recurrence Relations • This shows that if f(n) is the total number of bit operations needed to multiply two n-bit integers, then f(2 n) = 3 f(n) + Cn • This reasoning behind this equation is as follows. • The three multiplications of n-bit integers are carried out using 3 f(n)-bit operations. 5

Divide-and-Conquer Algorithms and Recurrence Relations • Theorem 1: let f be an increasing function that satisfies the recurrence relation f(n)= af(n/b) + c • Whenever n is divisible by b, where a≧ 1 , b is an integer greater than 1, and c is a positive real number. Then f(n) is O(nlogb a) if a >1 , O(log n) if a =1 • when n=bk , where k is a positive integer, f(n) = C 1 nlogba +C 2 = C 1 ak +C 2 where C 1= f(1)+c/(a-1) and C 2 = -c/(a-1). 6

Divide-and-Conquer Algorithms and Recurrence Relations • Example 6: Let f(n) = 5 f(n/2) + 3 and f(1) =7. Find f(2 k), where k is a positive integer. Also , estimate f(n) if f is an increase function. • Example 7: Estimate the number of comparisons used by a binary search. f(n) = f(n/2) + 2. • Example 8: Estimate the number of comparisons used to locate the maximum and minimum elements in a sequence using the algorithm given in example 2. f(n) = 2 f(n/2) + 2. 7

Divide-and-Conquer Algorithms and Recurrence Relations • Theorem 2: Master Theorem Let f be an increasing function that satisfies the recurrence relation f(n)= af(n/b) + cnd Whenever n=bk, where k is a positive integer, a≧ 1, b is an integer greater than 1, and c and d are real numbers with c positive and d nonnegative. Then f(n) is O(nd) if a < bd , O(nd log n) if a= bd , O(n logba) if a > bd. 8

Divide-and-Conquer Algorithms and Recurrence Relations • Example 9: Complexity of Merge Sort In Example 3 we explained that the number of comparisons used by the merge sort to sort a list of n elements is less than M(n), where M(n)=2 M(n/2) +n. By the Master Theorem (Theorem 2) we find that M(n) is O(n logn) , which agrees with the estimate found in section 4. 4. • Example 10: Estimate the number of bit operations needed to multiply two n-bit integers using the fast multiplication algorithm described in Example 4. 9

Divide-and-Conquer Algorithms and Recurrence Relations • Example 11 : Estimate the number of multiplications and additions required to multiply two n x n matrices using the matrix multiplication algorithm referred to in example 5. The function for the number of multiplications and additions is f(n)=7 f(n/2)+(15/4)n 2. 10

Divide-and-Conquer Algorithms and Recurrence Relations • Example 12: The Closest-Pair Problem Consider the problem of determining the closest pair of points in a set of n points (x 1, y 2), . . . , (xn, yn) in the plane, where the distance between two points (xi, yi) and (xj, yj) is the usual Euclidean distance [ (xi -xj)2+ (yi - yj)2 ]0. 5. • This problem arises in many applications such as determining the closest pair of airplanes in the air space at a particular altitude being managed by an air traffic controller. • How can this closest pair of points be found in an efficient way? (FIGURE 1 ) 11

Divide-and-Conquer Algorithms and Recurrence Relations FIGURE 1 The Recursive Step of the Algorithm for Solving the Closest-Pair Problem. 12

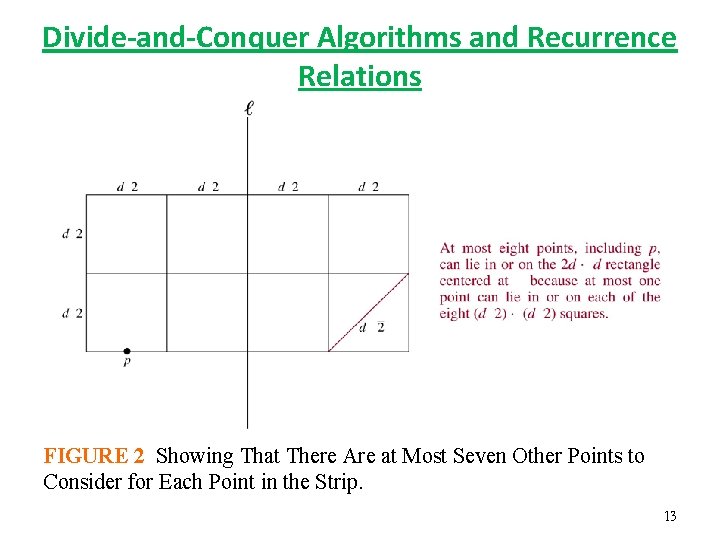
Divide-and-Conquer Algorithms and Recurrence Relations FIGURE 2 Showing That There Are at Most Seven Other Points to Consider for Each Point in the Strip. 13