Imagerie Mdicale Cours 3 Modles et outils fondamentaux

Imagerie Médicale Cours 3 : Modèles et outils fondamentaux pour le traitement d’image Formation ISIS UJFC Castres Clovis Tauber tauber@enseeiht. fr 05 61 58 80 67

Plan du cours • Introduction – Bibliographie – Intérêt du traitement d’image en imagerie médicale • Modèles fondamentaux – – – Modèle linéaire (convolution) Modèle fréquentiel (fourier. . . ) Modèle statistique (histogramme, entropie. . . ) Modèle différentiel (gradient, EDP. . . ) Modèle ensembliste (morphologie. . . ) Modèle discret (maillage, connexité, distance. . . ) • Exercices applicatifs

Bibliographie • • J. P. Cocquerez et S. Philipp « Analyse d'images : filtrage et segmentation » Masson 1995 R. C. Gonzalez et Woods « Digital Image Processing 2 d edition » Addison Wesley 2002 A. Rosenfeld et A. C. Kak « Digital picture processing » Academic Press London 1982. H. Maître (ss la direction de) « Le traitement des images » Hermes Lavoisier IC 2 2003. J. R. Parker « Algorithms for Image Processing and Computer Vision » Wiley & Sons 1997. S. Bres, J. M. Jolion, F. Lebourgeois « Traitement et analyse des images numériques» Hermes Lavoisier 2003 I. T. Young, J. J. Gerbrands et L. J. Van Vliet « Fundamentals of Image Processing » Université de Delft. (sur internet : http: //www. ph. tn. tudelft. nl/~lucas/publications/1995/FIP 95 TYJGLV/FIP 2. 2. pdf) D. Lingrand « Introduction au Traitement d'images » Vuibert 2004

Traiter une image ? • Image = matrice à n dimensions (2, 3, 4) • Information = quantités numériques • Traiter une image = manipuler l’information pour – Extraire de l’information – Transformer l’information

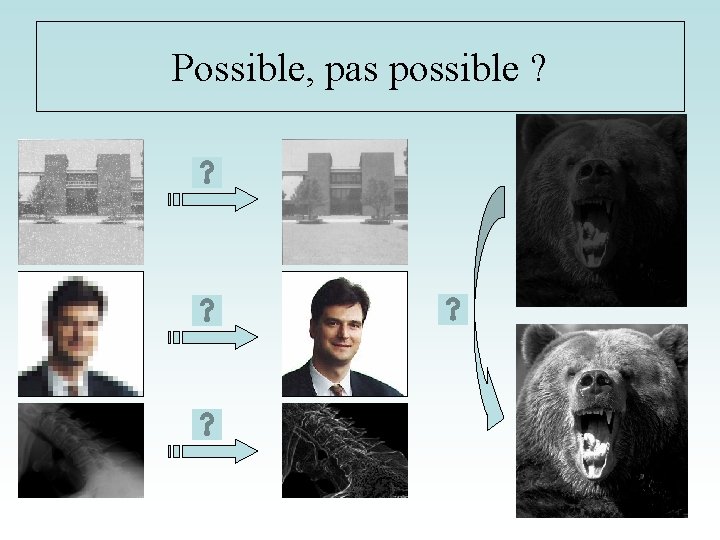
Possible, pas possible ?

En vue des exercices • Installation de Image. J Télécharger sur internet ou depuis le Cdrom du cours Logiciel prévu pour le traitement d’images : possibilité de créer des modules spécifiques • Traitement d’images = modèles mathématiques traduits en algorithmes Peut se faire avec tout langage de programmation (Matlab, C++ …)

Complexité (et subjectivité) de la perception visuelle Lancez Image. J et comparez les intensités des cases A et B Mécanismes en jeu sur l’exemple: • Renforcement local des contraste • Interprétation de l’ombre • Reconnaissance d’un échiquier

Enjeux du traitement d’image en imagerie médicale • Améliorer la perception de l’information dans les images • Détecter des objets • Extraire des indicateurs quantitatifs et qualitatifs • Permettre la comparaison d’informations Aide au diagnostic, Mesure de l’influence de thérapeutiques, Indexation des données …

Modèles mathématiques fondamentaux

Modèle linéaire • Description de l’image : espace vectoriel • Opérateurs qui préservent la structure d'espace vectoriel : les applications linéaires f (I+J) = f (I) + f(J) f(I) = f( I) • En traitement d’image : Convolutions

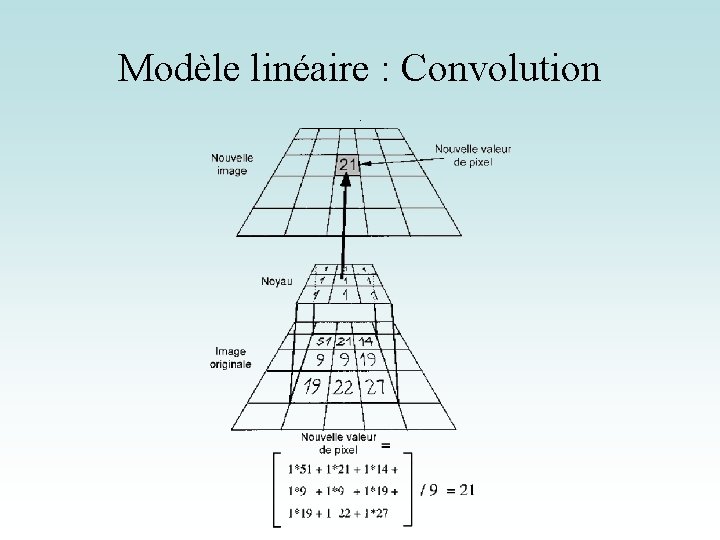
Modèle linéaire : Convolution

Modèle linéaire : Convolution • Application au cas d’une matrice (image) – Soit I une image numérique. – Soit h une fonction de [x 1, x 2]×[y 1, y 2] à valeurs réelles. h[x, y] La fonction h est appellée noyau de convolution Les nouvelles valeurs des pixels de I sont calculées par produit scalaire entre le noyau et le voisinage correspondant du pixel. Importance de la norme du noyau Conditions aux bords de l’image

Modèle linéaire : Convolution

Modèle linéaire : Convolution • Gestion des effets de bords: – – – Pixels à 0 ou 255; Pixels identiques; Miroir; Image périodique; Ignorer m/2 pixels sur le bord. Exemple sur le bord haut • La dimension du masque définit la localité de l’effet de la convolution.

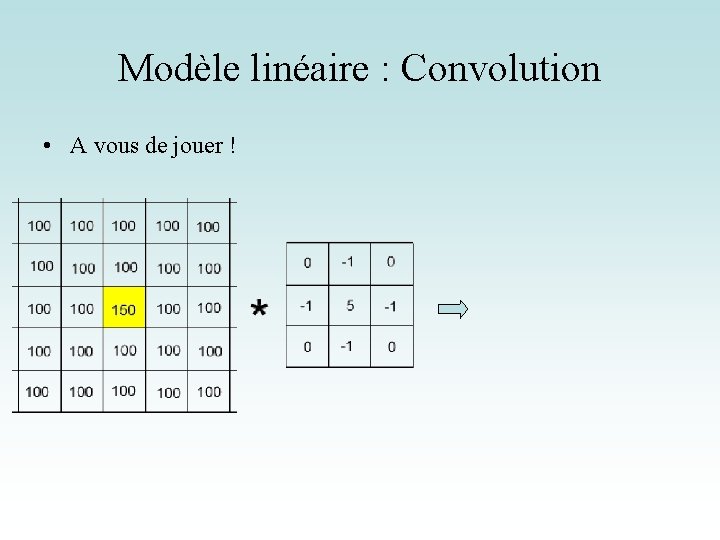
Modèle linéaire : Convolution • A vous de jouer !

Modèle linéaire : Convolution • La convolution dans le traitement d’images : – Filtrage linéaire des bruits – Détection de contours – Rehaussement de contraste

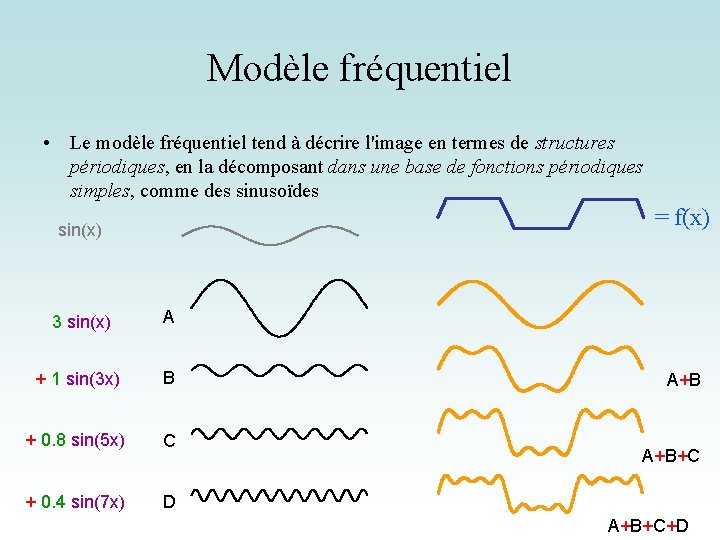
Modèle fréquentiel • Le modèle fréquentiel tend à décrire l'image en termes de structures périodiques, en la décomposant dans une base de fonctions périodiques simples, comme des sinusoïdes = f(x) sin(x) 3 sin(x) A + 1 sin(3 x) B + 0. 8 sin(5 x) C + 0. 4 sin(7 x) D A+B+C+D

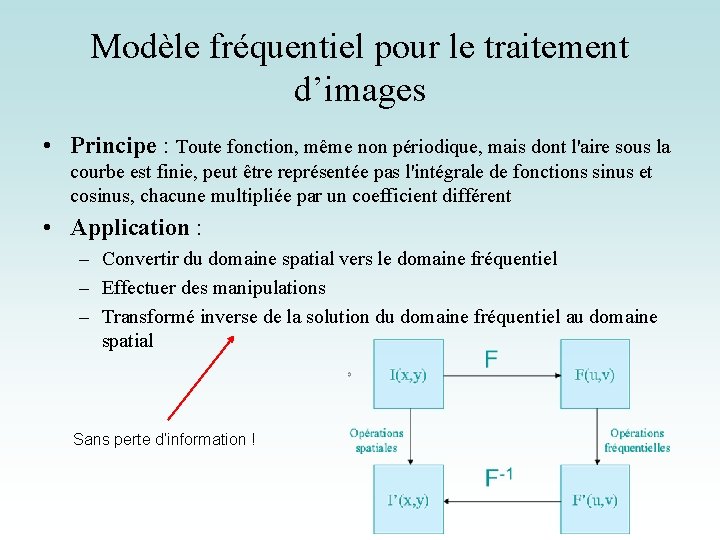
Modèle fréquentiel pour le traitement d’images • Principe : Toute fonction, même non périodique, mais dont l'aire sous la courbe est finie, peut être représentée pas l'intégrale de fonctions sinus et cosinus, chacune multipliée par un coefficient différent • Application : – Convertir du domaine spatial vers le domaine fréquentiel – Effectuer des manipulations – Transformé inverse de la solution du domaine fréquentiel au domaine spatial Sans perte d’information !

Modèle fréquentiel : rappel sur les nombres complexes Partie Imaginaire Z=(a, b) b |Z| a Partie Réelle

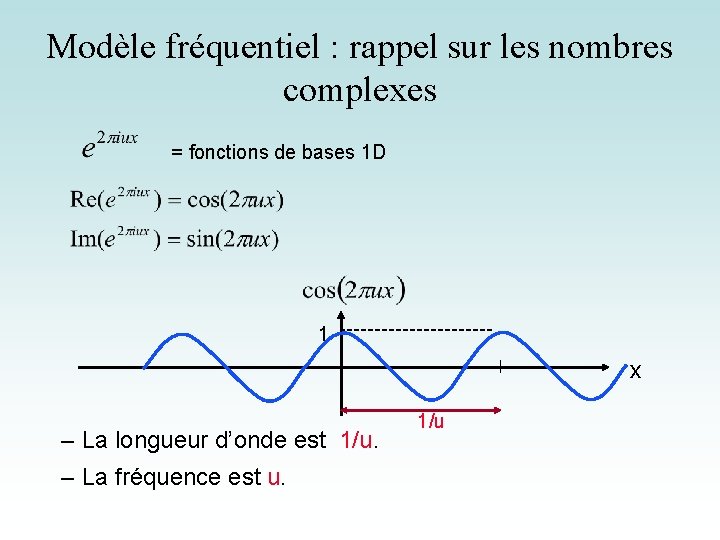
Modèle fréquentiel : rappel sur les nombres complexes = fonctions de bases 1 D 1 x – La longueur d’onde est 1/u. – La fréquence est u. 1/u

Modèle fréquentiel : transformée de Fourier • La transformée de Fourier permet la décomposition d'un signal f en combinaison linéaire de sinusoïdes complexes • Les coefficients F[u, v] dit coefficients de Fourier, fournissent des informations sur les fréquences (u, v) et permettent des manipulations dans le domaine fréquentiel

Modèle fréquentiel : transformée de Fourier • Transformation de Fourier discrète • On appelle la fonction F(u, v) le spectre (u = 0, . . . , N-1; v = 0, …, M-1) (x = 0, . . . , N-1; y = 0, …, M-1)

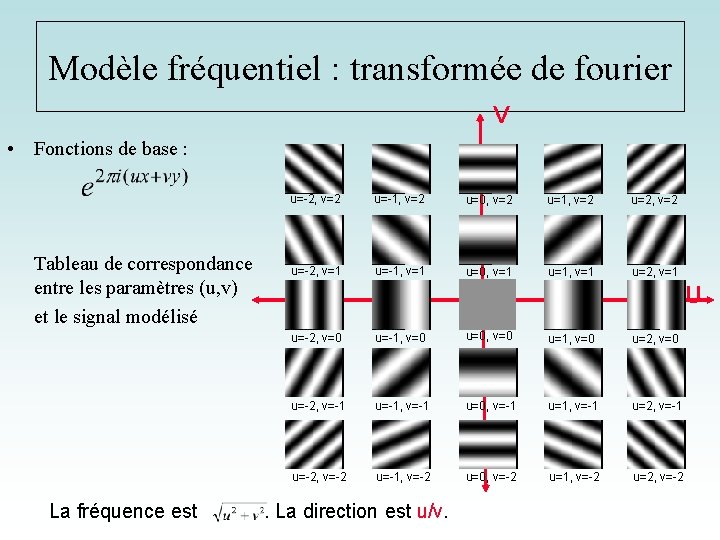
Modèle fréquentiel : transformée de fourier V • Fonctions de base : Tableau de correspondance entre les paramètres (u, v) et le signal modélisé La fréquence est u=-2, v=2 u=-1, v=2 u=0, v=2 u=1, v=2 u=2, v=2 u=-2, v=1 u=-1, v=1 u=0, v=1 u=1, v=1 u=2, v=1 U u=-2, v=0 u=-1, v=0 u=0, v=0 u=1, v=0 u=2, v=0 u=-2, v=-1 u=-1, v=-1 u=0, v=-1 u=1, v=-1 u=2, v=-1 u=-2, v=-2 u=-1, v=-2 u=0, v=-2 u=1, v=-2 u=2, v=-2 . La direction est u/v.

Modèle fréquentiel : transformée de Fourier • Représentation transformée 2 D : image à valeurs complexes • Décomposition du spectre en images visibles : – Spectre d’amplitude – Spectre de phase • Pour l’affichage on peut utiliser log(1 + |F(u, v)|) Importance des deux composantes Image reconstruite à l’aide de l’amplitude uniquement Image reconstruite à l’aide de la phase uniquement

Modèle fréquentiel : transformée de Fourier Phase d’une image plus amplitude de l’autre

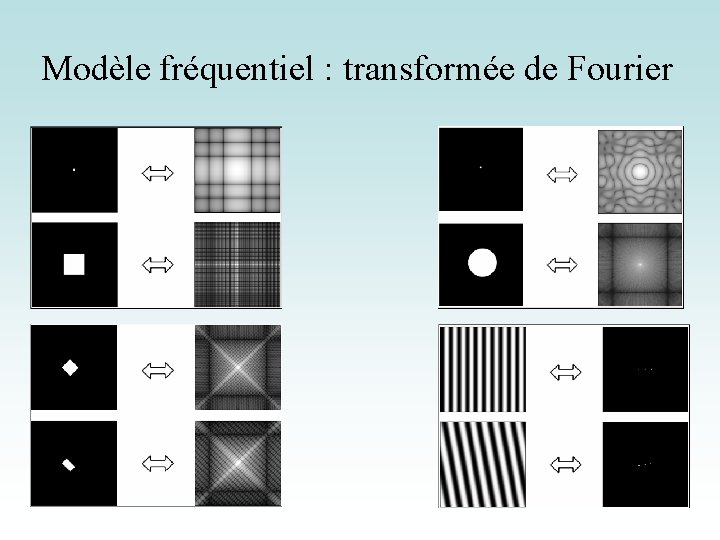
Modèle fréquentiel : transformée de Fourier

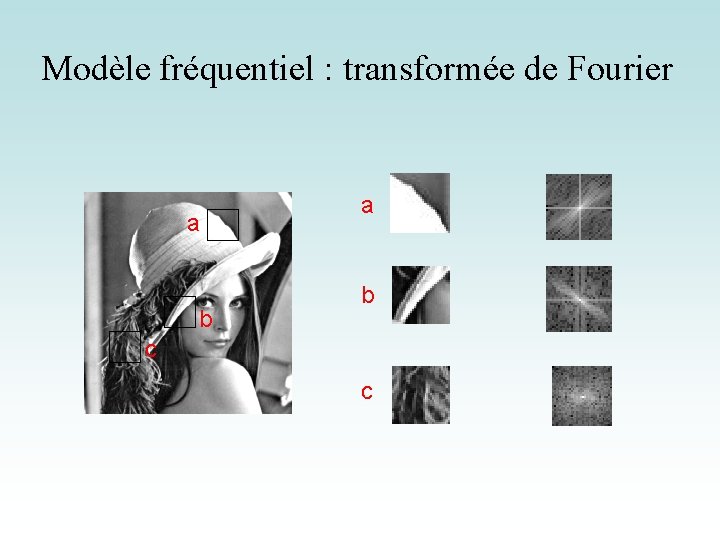
Modèle fréquentiel : transformée de Fourier a b c c

Quizz : associez à chaque image son spectre

Modèle statistique • On s'intéresse dans ce modèle aux propriétés statistiques des images : la distribution des valeurs prises par les pixels, la corrélation existant entre des pixels spatialement proches, la fréquence d'occurrence de certaines structures spatiales. . . • Les mesures statistiques fournissent des grandeurs et fonctions empiriques sur lesquelles peuvent s'appuyer des modèles probabilistes utilisés par les algorithmes d'analyse d'images. – Champs de Markov : chaque pixel correspondant à une variable aléatoire dont la valeur ne dépend que de celle de ses voisins – Matrices de cooccurrence : texture – …

Modèle statistique : l’histogramme • L'histogramme représente la répartition des pixels en fonction de leur niveau de gris. Il fournit diverses informations comme les statistiques d'ordre, l'entropie, et peut permettre d'isoler des objets. Occurrence (nb de pixels) 0 255 Niveaux de gris

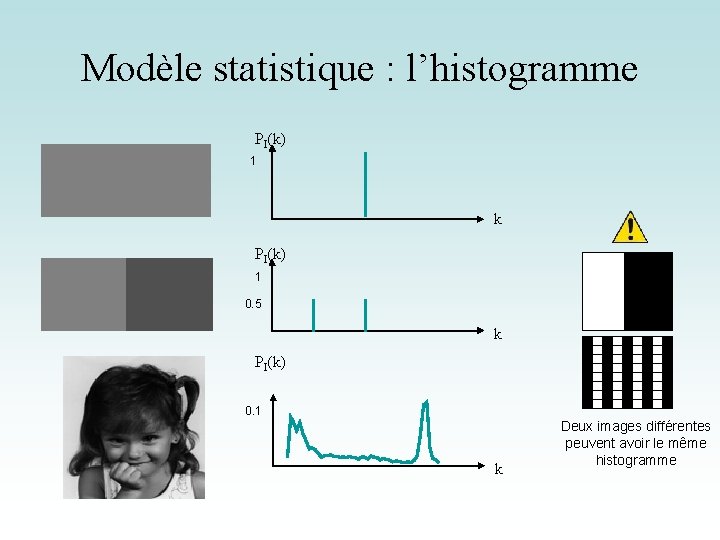
Modèle statistique : l’histogramme PI(k) 1 k PI(k) 1 0. 5 k PI(k) 0. 1 k Deux images différentes peuvent avoir le même histogramme

Modèle statistique : l’histogramme • Nous citons ici trois traitements d’image classiques à partir de l’histogramme : – La normalisation d’histogramme : Exploitation de toute la dynamique de codage – L’égalisation d’histogramme : Équilibrer la dynamique du codage et augmenter le contraste – La segmentation d’histogramme, dont le célèbre seuillage : Simplifier l’image en regroupant les pixels selon leur valeur

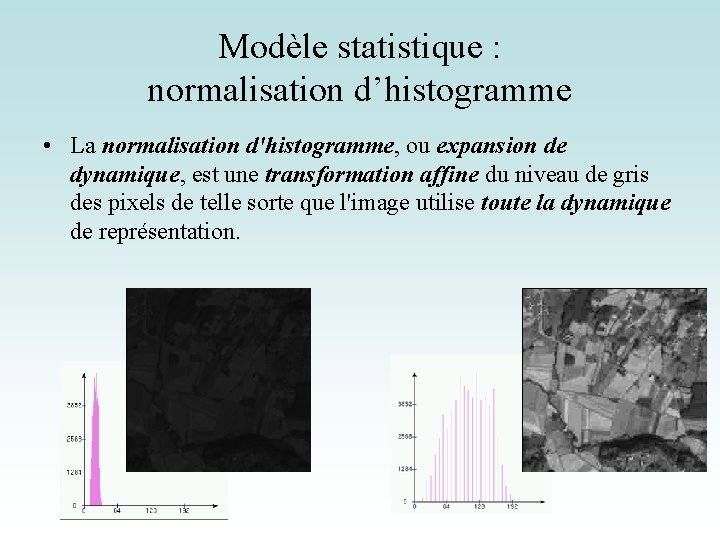
Modèle statistique : normalisation d’histogramme • La normalisation d'histogramme, ou expansion de dynamique, est une transformation affine du niveau de gris des pixels de telle sorte que l'image utilise toute la dynamique de représentation.

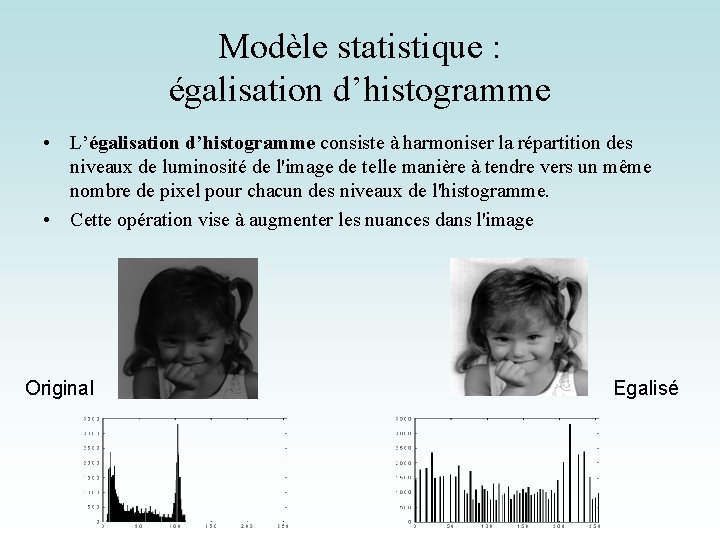
Modèle statistique : égalisation d’histogramme • L’égalisation d’histogramme consiste à harmoniser la répartition des niveaux de luminosité de l'image de telle manière à tendre vers un même nombre de pixel pour chacun des niveaux de l'histogramme. • Cette opération vise à augmenter les nuances dans l'image Original Egalisé

Modèle statistique : égalisation d’histogramme • La technique classique consiste à rendre « le plus linéaire possible » l'histogramme cumulé de l'image Histogrammes cumulés

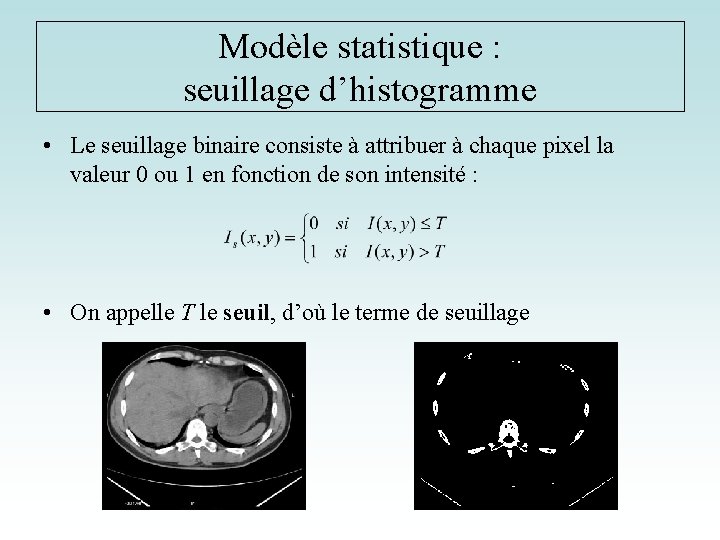
Modèle statistique : seuillage d’histogramme • Le seuillage binaire consiste à attribuer à chaque pixel la valeur 0 ou 1 en fonction de son intensité : • On appelle T le seuil, d’où le terme de seuillage

Modèle statistique : seuillage d’histogramme • Problème : trouver le bon seuil (si il existe)

Modèle statistique : seuillage d’histogramme • Utilisation de l’histogramme pour trouver le seuil

Modèle statistique : seuillage d’histogramme • Seuillage adaptatif : la valeur du seuil varie avec un critère c(x, y) calculé dans le voisinage du pixel en question • Seuillage dynamique : la valeur du seuil varie avec la localisation du pixel Dans cet exemple le seuil est la valeur moyenne d’une fenêtre 5 x 5 centrée en (x, y)

Modèle différentiel • Dans le modèle différentiel, on considère l'image comme une fonction continue f(x, y), dont on étudie le comportement local à l'aide de ses dérivées. • Une telle étude, fondée sur la formule de Taylor, n'a de sens que si la fonction f a une certaine régularité, ce qui constitue le problème clef des méthodes différentielles

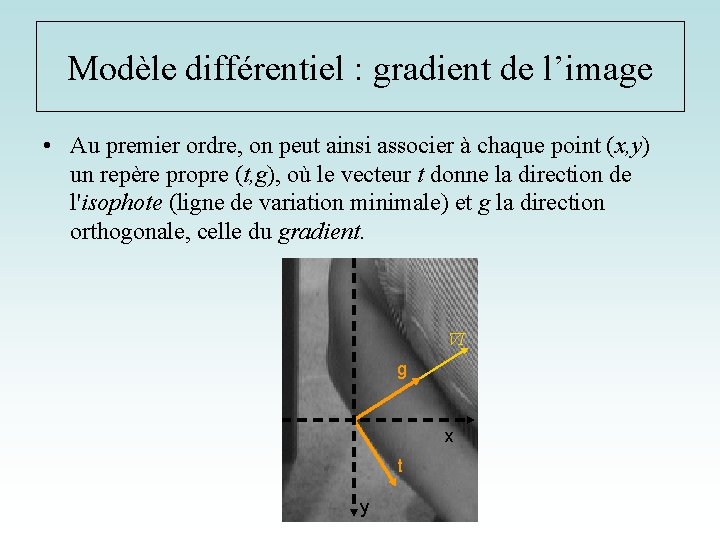
Modèle différentiel : gradient de l’image • Au premier ordre, on peut ainsi associer à chaque point (x, y) un repère propre (t, g), où le vecteur t donne la direction de l'isophote (ligne de variation minimale) et g la direction orthogonale, celle du gradient. I g x t y

Modèle différentiel : gradient de l’image • Grâce au plongement dans le continu, le modèle différentiel permet en outre d'exprimer un grand nombre d'opérations d'analyse en termes d'équations aux dérivées partielles (EDP), ce qui permet de donner un fondement mathématique satisfaisant aux traitements et aussi de fournir des méthodes pour les calculer, par des schémas numériques de résolutions – – Diffusion anisotrope Contours actifs Ensembles de niveau ….

Modèle ensembliste • En morphologie mathématique, l'image est considérée comme un ensemble, dont on étudie les propriétés en fonction de relations locales avec un ensemble de référence (élément structurant) en termes d'intersection et d'inclusion (relations en tout-ou-rien). • Les opérateurs morphologiques élémentaires sont – L’érosion – La dilatation • D’autres opérateurs plus complexes peuvent être obtenus en combinant l’érosion et la dilatation : – L’ouverture – La fermeture • La squelettisation fait aussi partie des opérateurs morphologiques

Modèle ensembliste : l’érosion • Sur une image binaire l'érosion diminue la taille des structures, et élimine les objets de taille inférieure à l'élément structurant. Elle permet de séparer les objets reliés. • Sur une image en niveaux de gris l'érosion diminue les niveaux de gris et augmente la taille des trous dans les objets. Points x tels que l’élément structurant centré en x est inclus dans X Bx élément structurant

Modèle ensembliste : l’érosion Elément Structurant Pablo Picasso

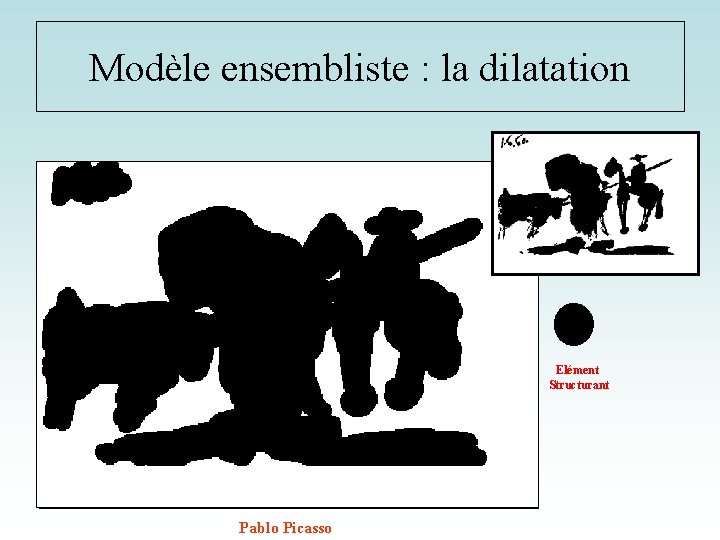
Modèle ensembliste : la dilatation • La dilatation est l’inverse de l'erosion. Elle grossit tous les objets en fonction de la taille de l'élément structurant. • Les trous plus petits que l’élément structurant sont comblés • Les objets situés à une distance inférieure à la taille de l'élément sont fusionnés Points x tels que l’élément structurant centré a une intersection nulle avec X Bx élément structurant

Modèle ensembliste : la dilatation Elément Structurant Pablo Picasso

Modèle ensembliste : dilatation et érosion fonctionnelles : niveaux de gris • Sur une image en niveaux de gris l'érosion consiste à donner à tout pixel la valeur minimale de l'image dans la fenêtre d'observation définie par l’élément structurant. • L'érosion tend à homogénéiser l'image (réduction des pics de niveaux de gris), à l'assombrir et à étaler le bord des objets les plus sombres. • Sur une image en niveaux de gris la dilatation consiste à donner à tout pixel la valeur maximale de l'image dans la fenêtre d'observation définie par l’élément structurant. • La dilatation tend à homogénéiser l'image (épaississement des pics), à l'éclaircir et à faire disparaître les objets sombres.

Modèle ensembliste : l’ouverture • Une érosion suivie d'une dilatation s’appelle une ouverture. • Comme le montre l’exemple, l’ouverture a pour propriété d'éliminer toutes les parties des objets qui ne peuvent pas contenir l’élément structurant.

Modèle ensembliste : la fermeture • Une dilatation suivie d'une érosion s’appelle une fermeture. • Comme le montre l’exemple, la fermeture a pour propriété de combler tout ce qui est de taille inférieure à l’élément structurant.

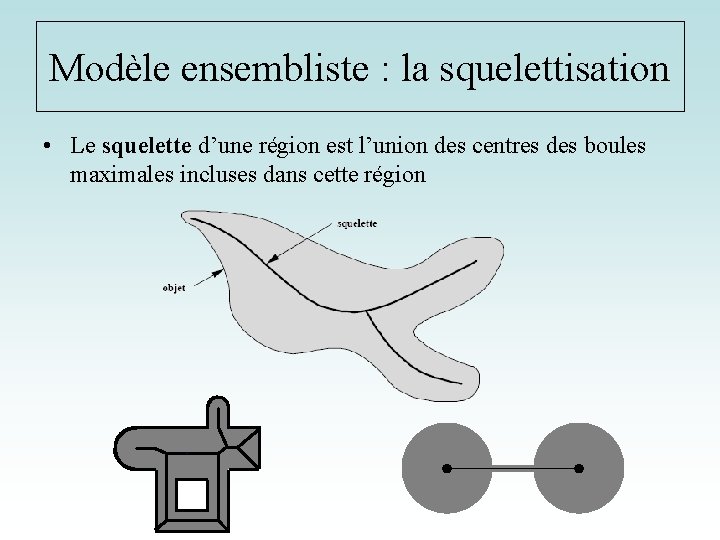
Modèle ensembliste : la squelettisation • Le squelette d’une région est l’union des centres des boules maximales incluses dans cette région

Quizz : trouvez l’enchaînement d’opérations :

A vous de jouer !

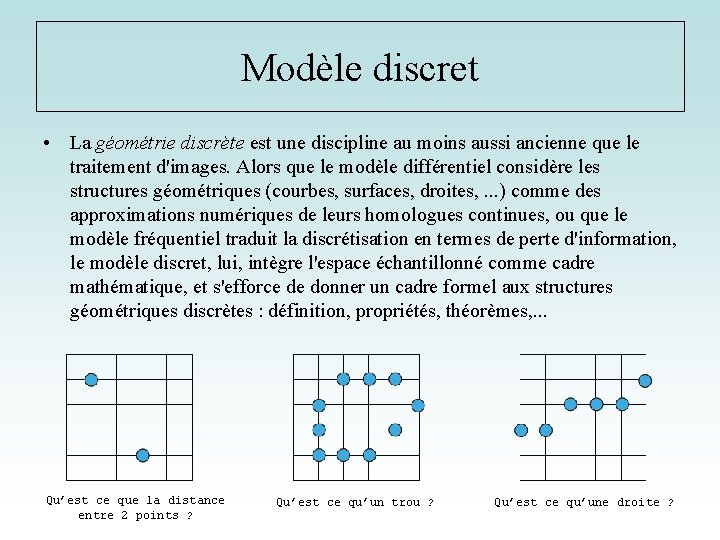
Modèle discret • La géométrie discrète est une discipline au moins aussi ancienne que le traitement d'images. Alors que le modèle différentiel considère les structures géométriques (courbes, surfaces, droites, . . . ) comme des approximations numériques de leurs homologues continues, ou que le modèle fréquentiel traduit la discrétisation en termes de perte d'information, le modèle discret, lui, intègre l'espace échantillonné comme cadre mathématique, et s'efforce de donner un cadre formel aux structures géométriques discrètes : définition, propriétés, théorèmes, . . . Qu’est ce que la distance entre 2 points ? Qu’est ce qu’un trou ? Qu’est ce qu’une droite ?

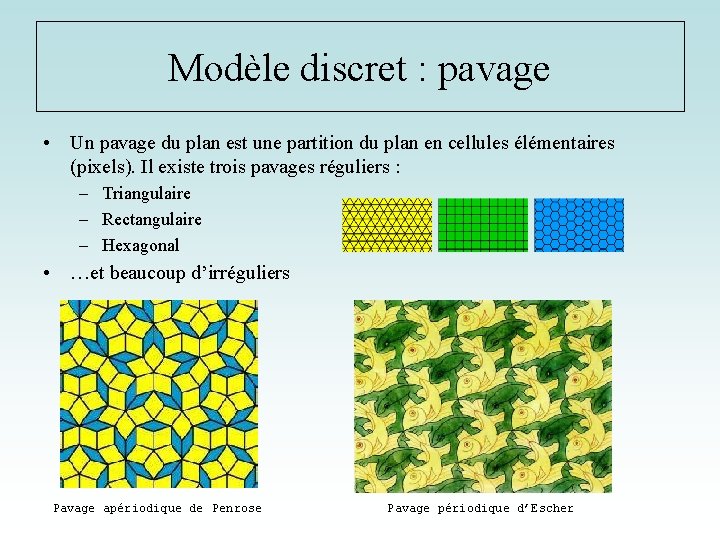
Modèle discret : pavage • Un pavage du plan est une partition du plan en cellules élémentaires (pixels). Il existe trois pavages réguliers : – Triangulaire – Rectangulaire – Hexagonal • …et beaucoup d’irréguliers Pavage apériodique de Penrose Pavage périodique d’Escher

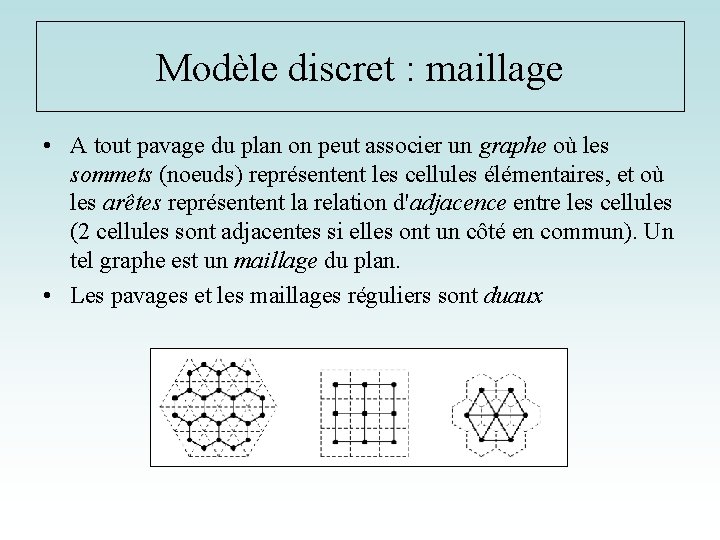
Modèle discret : maillage • A tout pavage du plan on peut associer un graphe où les sommets (noeuds) représentent les cellules élémentaires, et où les arêtes représentent la relation d'adjacence entre les cellules (2 cellules sont adjacentes si elles ont un côté en commun). Un tel graphe est un maillage du plan. • Les pavages et les maillages réguliers sont duaux

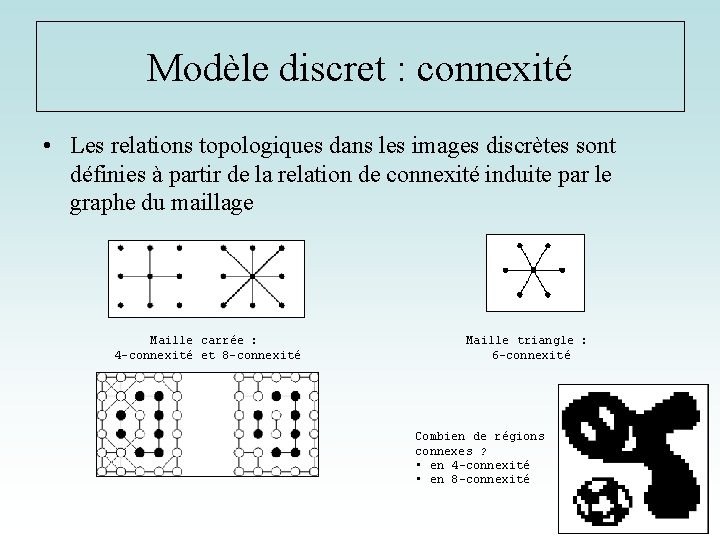
Modèle discret : connexité • Les relations topologiques dans les images discrètes sont définies à partir de la relation de connexité induite par le graphe du maillage Maille carrée : 4 -connexité et 8 -connexité Maille triangle : 6 -connexité Combien de régions connexes ? • en 4 -connexité • en 8 -connexité

Modèle discret : distance • Comment calculer la distance entre deux pixels P(xp, yp) et Q(xq, yq) ? – distance de Manathan : d 1(P, Q)=|xp - xq| + |yp - yq| – distance euclidienne : d 2(P, Q)=[(xp - xq)2 + (yp - yq)2]1/2 – distance de l'échiquier : dinf(P, Q)=Max(|xp - xq| , |yp - yq|) dinf(P, Q) d 2(P, Q) d 1(P, Q)

Conclusion • A retenir de ce cours : – – – Objectifs et limites du traitement d’image Convolution Représentation fréquentielle Opérateurs morphologiques Histogramme Connexité et distance discrètes

Exercice 1 : segmentation en contours minces • Une image I de taille 10 x 10 est représentée par un tableau de valeurs. On se propose de mettre en place un algorithme permettant d'extraire les points contour d'une image en utilisant uniquement des opérateurs morphologiques et le seuillage. • Les pixels concernés par l'effet de bord seront calculés sans considérer les valeurs extérieures au domaine de l’image.

Exercice 1 : segmentation en contours minces • Effectuer les opérations suivantes (en utilisant les grilles prévues à cet effet sur la feuille n° 1) 1. 2. 3. 4. Id= Dilatation(I) Ie = Erosion(I) I 1 = Id - I I 2 = I - Ie Bx élément structurant

Exercice 1 : segmentation en contours minces • • On opère maintenant un seuillage sur les images I 1 et I 2 pour former respectivement IS 1 et IS 2. Représenter sur les grilles de la feuille fournie le résultat des procédures décrites ci-dessous en noircissant les pixels à 1, les autres étant laissés en blanc : 1. seuillage I 1 : pour tout x, y : IS 1(x, y) = 1 si I 1(x, y) >= 2 ; sinon IS 1(x, y) = 0 2. seuillage I 2 : pour tout x, y : IS 2(x, y) = 1 si I 2(x, y) >= 2 ; sinon IS 2(x, y) = 0 • • Les opérations permettant d’obtenir I 1 et I 2 sont deux opérateurs appelés "Gradient morphologique" Quelles différences y a-t-il entre GD et GE ?

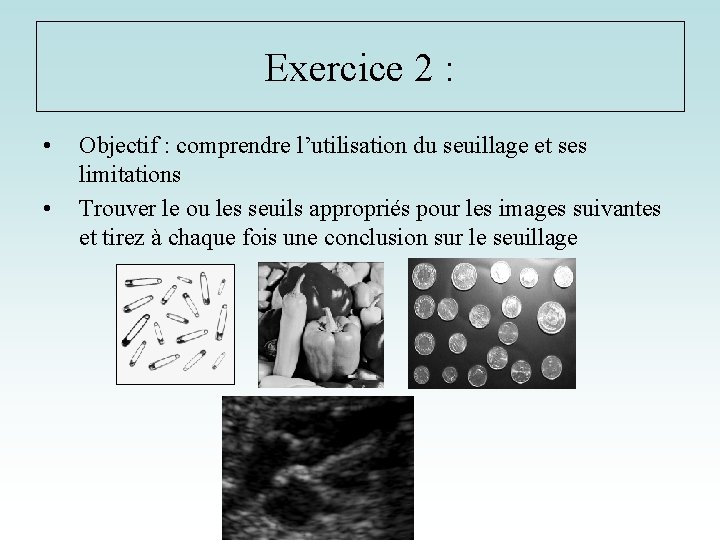
Exercice 2 : • • Objectif : comprendre l’utilisation du seuillage et ses limitations Trouver le ou les seuils appropriés pour les images suivantes et tirez à chaque fois une conclusion sur le seuillage

Exercice 2 b : • • • Trouvez un seuil approprié pour détecter les vis dans les images suivantes Imaginez une méthode pour améliorer le résultat Quel est le défaut de la méthode ?

Exercice 3 : • • • Affichez l’histogramme de l’image « bear. png » Analysez le problème Appliquez une solution et vérifiez l’histogramme du résultat

Pour le prochain cours • Comment peut-on utiliser la convolution pour le filtrage et la segmentation ? • Qu’est ce que la DCT ? Différence avec la DFT ? • A quoi sert le recalage d’image dans le domaine de la santé ? Répondre à chaque question en 3 à 5 lignes