Gases CHAPTER 10 Powerpoint from Melissa Brophys website

Gases CHAPTER 10 • Powerpoint from Melissa Brophy’s website (http: //teacherweb. com/TX/Mc. Neil. HS/brophy/ photo 7. aspx) and modified for our class

Resources and Activities • Textbook - chapter 10 & ppt file Gases (Chapter 10) • Online practice quiz from Pearson chapter 10 • Lab activities (1) Molar volume of a gas (wet lab) (2) Virtual labs: gas laws (next slide) • POGIL activities: Ideal gas law Partial Pressure • Comprehensive tutorial and animations on Intermolecular forces : http: //www. chem. purdue. edu/gchelp/liquids/imf 2. html Chemtour videos from W. W. Norton (chapter 6 : ideal gas law; Dalton’s law; molecular speed) http: //www. wwnorton. co m/college/chemistry/ gilbert 2/contents/ch 0 6/studyplan. asp See NEXT SLIDE

Animation on gases to view in class: http: //glencoe. com/sites/common_assets/advanced_placement/chemistry_ chang 9 e/animations/chang_7 e_esp/gam 2 s 2_6. swf Independent work - students to view animations & interactive activities (4 in total) and write summary notes on each. These summaries are to be included in your portfolio http: //glencoe. mcgrawhill. com/sites/0035715985/student_view 0/chapter 5/animations_center. html# Virtual lab activity (To complete at home and to hand in for grading) • Boyle’s Law Objective: Explore the effects of V on P at constant T (for a fixed quantity of gas molecules ). Task: Generate, record and graph data for three gases. Print and Discuss your results. Go to: http: //www. chem. iastate. edu/group/Greenbowe/sections/projectfolder/flashfiles/gaslaw/boyl es_law_graph. html • Charles Law Objective: Explore the effect of T on V at constant P (for a fixed quantity of gas molecules). Task: generate, record and graph data. Print and discuss your results. Go to: http: //www. chem. iastate. edu/group/Greenbowe/sections/projectfolder/flashfiles/gaslaw/ch arles_law. html

Activities and Problem set for chapter 10 (due date_______) Text. Book ch. 10– all sections required for regents (in part), SAT II and AP exams • Complete the chapter 10 packet part (a) Characteristics of Gases ( sample, practice and integrative exercises - show work) and part (b) Lab activities: (wet lab and virtual lab) POGILS (2) AP Chemistry Gas Law Practice • Do all chapter 10 GIST and Visualizing concepts problems - Online practice quiz ch 10 due by_____ write out questions and answers & show work. (NB Photocopy of questions is also acceptable)

Measurements on Gases • Properties of gases – – Gases uniformly fill any container Gases are easily compressed Gases mix completely with any other gas Gases exert pressure on their surroundings • Pressure = Force Area

Measurements on Gases • Measuring pressure – The barometer – measures atmospheric pressure • Inventor – Evangelista Torricelli (1643)

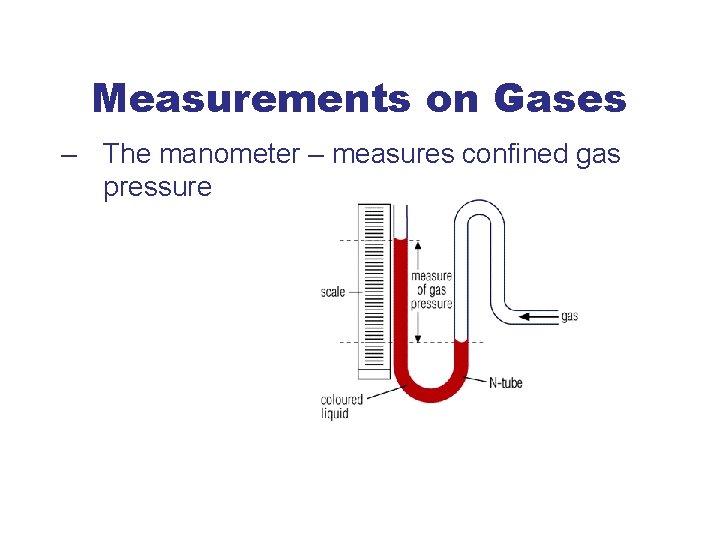
Measurements on Gases – The manometer – measures confined gas pressure

Measurements on Gases – Units • mm Hg (torr) – • Kilopascal (k. Pa) – • 101. 325 k. Pa = standard pressure Atmospheres – • 760 torr = standard pressure 1 atmosphere (atm) = standard pressure STP = 1 atm = 760 torr = 760 mm. Hg = 101. 325 k. Pa

Measurements on Gases • Example: Convert 0. 985 atm to torr and to k. Pa. 0. 985 atm 760 torr 1 atm 0. 985 atm 101. 325 k. Pa 1 atm = 749 torr = 98. 3 k. Pa

The Gas Laws of Boyle, Charles and Avogadro • Boyle’s Law (Robert Boyle, 16271691) – The product of pressure times volume is a constant, provided the temperature remains the same • PV = k

The Gas Laws of Boyle, Charles and Avogadro • • • P is inversely related to V The graph of P versus V is hyperbolic Volume increases linearly as the pressure decreases – As you squeeze a zip lock bag filled with air (reducing the volume), the pressure increases making it difficult to keep squeezing

The Gas Laws of Boyle, Charles and Avogadro – At constant temperature, Boyle’s law can be used to find a new volume or a new pressure • P 1 V 1 = k = P 2 V 2 or P 1 V 1 = P 2 V 2 – – Boyle’s law works best at low pressures Gases that obey Boyle’s law are called Ideal gases

The Gas Laws of Boyle, Charles and Avogadro • Example: A gas which has a pressure of 1. 3 atm occupies a volume of 27 L. What volume will the gas occupy if the pressure is increased to 3. 9 atm at constant temperature? • • P 1 = 1. 3 atm V 1 = 27 L P 2 = 3. 9 atm V 2 = ? (1. 3 atm)(27 L) = (3. 9 atm)V 2 = 9. 0 L

The Gas Laws of Boyle, Charles and Avogadro • Charles’ Law (Jacques Charles, 1746 – 1823) – The volume of a gas increase linearly with temperature provided the pressure remains constant V = b. T V=b T or V 1 = V 2 T 1 T 2 V 1 = b = V 2 T 1 T 2

The Gas Laws of Boyle, Charles and Avogadro • Temperature must be measured in Kelvin ( K = °C + 273) – 0 K is “absolute zero”

The Gas Laws of Boyle, Charles and Avogadro • Example: A gas at 30°C and 1. 00 atm has a volume of 0. 842 L. What volume will the gas occupy at 60°C and 1. 00 atm? • V 1 = 0. 842 L • T 1 = 30°C (+273 = 303 K) • V 2 = ? • T 2 = 60°C (+273 = 333 K)

0. 842 L 303 K V 2 = 0. 925 L = V 2 333 K

The Gas Laws of Boyle, Charles and Avogadro • Avogadro’s Law (Amedeo Avogadro, 1811) – For a gas at constant temperature and pressure, the volume is directly proportional to the number of moles, n • V = an V 1 = a = V 2 n 1 n 2 V/n = a or V 1 = V 2 n 1 n 2

The Gas Laws of Boyle, Charles and Avogadro • Example: A 5. 20 L sample at 18°C and 2. 00 atm contains 0. 436 moles of a gas. If we add an additional 1. 27 moles of the gas at the same temperature and pressure, what will the total volume occupied by the gas be? • V 1 = 5. 20 L • n 1 = 0. 436 mol • V 2 = ? • n 2 = 1. 27 mol + 0. 436 mol = 1. 706 mol

The Gas Laws of Boyle, Charles and Avogadro 5. 20 L = V 2 0. 436 mol 1. 706 mol x = 20. 3 L

The Ideal Gas Law • Derivation from existing laws V=k V=b. T V=an P V = kba(Tn) P

The Ideal Gas Law Constants k, b, a are combined into the universal gas constant (R), V = n. RT P or PV = n. RT

The Ideal Gas Law R = PV using standard numbers will give you R n. T STP • P = 1 atm • V = 22. 4 L • n = 1 mol • T = 273 K • Therefore if we solve for R, R = 0. 0821 L • atm/mol • K

The Ideal Gas Law • Example: A sample containing 0. 614 moles of a gas at 12°C occupies a volume of 12. 9 L. What pressure does the gas exert? P=? V = 12. 9 L n = 0. 614 mol R = 0. 0821 L • atm/mol • K T = 12 + 273 = 285 K

The Ideal Gas Law (P)(12. 9 L) = (0. 614 mol)(0. 0821 L • atm/mol • K)(285 K) Hint: Rearrange and re-write (watch out for units in numerator and denominator) P =1. 11 atm

The Ideal Gas Law Solving for new volumes, temperature, or pressure (n remaining constant) • Combined Law P 1 V 1 = n. R = P 2 V 2 T 1 T 2 or P 1 V 1 = P 2 V 2 T 1 T 2

The Ideal Gas Law • Example: A sample of methane gas at 0. 848 atm and 4. 0°C occupies a volume of 7. 0 L. What volume will the gas occupy if the pressure is increased to 1. 52 atm and the temperature increased to 11. 0°C? • P 1 = 0. 848 atm P 2 = 1. 52 atm • V 1 = 7. 0 L V 2 = ? • T 1 = 4+273 = 277 K T 2 = 11+273 = 284 K

The Ideal Gas Law (0. 848 atm)(7. 0 L) 277 K V 2 = 4. 0 L = (1. 52 atm)(V 2) 284 K

Gas Stoichiometry • Molar volume – • One mole of an ideal gas occupies 22. 4 L of volume at STP Things to remember – Density = mass – volume n = grams of substance = m molar mass M • PV = m. RT M

Gas Stoichiometry • Example: A sample containing 15. 0 g of dry ice (CO 2(s)) is put into a balloon and allowed to sublime according to the following equation: CO 2(s) CO 2(g) How big will the balloon be (i. e. what is the volume of the balloon) at 22°C and 1. 04 atm, after all of the dry ice has sublimed?

Gas Stoichiometry • Moles of CO 2(s): 15 g 1 mol = 0. 341 mol CO 2(s) 44 g 0. 341 mol CO 2(s) 1 CO 2(g) = 0. 341 mol CO 2(g) 1 CO 2(s) =n

Gas Stoichiometry P = 1. 04 atm V=? n = 0. 341 mol R = 0. 0821 L • atm/mol • K T = 22 C + 273 = 295 K V = 7. 94 L

Gas Stoichiometry • Limiting Reactant Example: 0. 500 L of H 2(g) are reacted with 0. 600 L of O 2(g) at STP according to the equation 2 H 2(g) + O 2(g) 2 H 2 O(g) • What volume will the H 2 O occupy at 1. 00 atm and 350°C?

Gas Stoichiometry • H 2: 0. 5 L 1 mol 2 H 2 O = 0. 0223 mol H 2 O 22. 4 L 2 H 2 • O 2: 0. 6 L 1 mol 2 H 2 O = 0. 0536 mol H 2 O 22. 4 L 1 O 2

Gas Stoichiometry • H 2: (1 atm)(V) = (0. 0223 mol)(0. 0821 L • atm/mol • K)(623 K) V = 1. 14 L Limiting reactant and how much volume is produced! • O 2: (1 atm)(V) = (0. 0536 mol)(0. 0821 L • atm/mol • K)(623 K) V = 2. 74 L

Gas Stoichiometry • Density/Molar Mass example: A gas at 34°C and 1. 75 atm has a density of 3. 40 g/L. Calculate the molar mass of the gas. D = mass 3. 40 = 3. 40 g V 1 L P = 1. 75 atm V = 1 L m = 3. 40 g R = 0. 0821 L • atm/mol • K T = 34 + 273 = 307 K M=x

Gas Stoichiometry (1. 75 atm)(1 L) = (3. 4 g)(0. 0821 L • atm/mol • K)(307 K) M M = molar mass M = 48. 97 g/mol

Dalton’s Law of Partial Pressures (John Dalton, 1803) • Statement of law – “for a mixture of gases in a container, the total pressure exerted is the sum of the pressures each gas would exert if it were alone” – It is the total number of moles of particles that is important, not the identity or composition of the gas particles.

Dalton’s Law of Partial Pressures • Derivation – – – Ptotal = P 1 + P 2 + P 3 … P 1 = n 1 RT P 2 = n 2 RT P 3 = n 3 RT …. V V V Ptotal = n 1 RT + n 2 RT + n 3 RT V V V Ptotal = (n 1+n 2+n 3+…) (RT) V Ptotal = ntotal (RT) V

Dalton’s Law of Partial Pressures • Example: Oxygen gas is collected over water at 28 C. The total pressure of the sample is 5. 5 atm. At 28 C, the vapor pressure of water is 1. 2 atm. What pressure is the oxygen gas exerting? • Ptotal = PO 2 + PH 2 O • 5. 5 = x + 1. 2 • X = 4. 3 atm

Dalton’s Law of Partial Pressures • Mole Fraction – The ratio of the number of moles of a given component in a mixture to the total number of moles in the mixture – For an ideal gas, the mole fraction (x): x 1 = ntotal P 1 Ptotal

Dalton’s Law of Partial Pressures • Example: The vapor pressure of water in air at 28°C is 28. 3 torr. Calculate the mole fraction of water in a sample of air at 28°C and 1. 03 atm. • XH 2 O = PH 2 O = 28. 3 torr Pair 783 torr = 0. 036

Dalton’s Law of Partial Pressures • Example: A mixture of gases contains 1. 5 moles of oxygen, 7. 5 moles of nitrogen and 0. 5 moles of carbon dioxide. If the total pressure exerted is 800 mm. Hg, what are the partial pressures of each gas in the mixture?

Dalton’s Law of Partial Pressures • Calculate the total number of moles – 1. 5 + 7. 5 + 0. 5 = 9. 5 moles • Use mole fractions for each individual gas • PO 2: 800 mm. Hg x 1. 5 mol = 126 mm. Hg 9. 5 mol • PN 2: 800 mm. Hg x 7. 5 mol = 632 mm. Hg 9. 5 mol • PCO 2: 800 mm. Hg x 0. 5 mol = 42 mm. Hg 9. 5 mol

Kinetic Molecular Theory of Gases • Postulates of the KMT Related to Ideal Gases – – The particles are so small compared with the distances between them that the volume of the individual particles can be assumed to be zero The particles are in constant motion. Collisions of the particles with the walls of the container cause pressure. Assume that the particles exert no forces on each other The average kinetic energy of a collection of gas particles is assumed to be directly proportional to the Kelvin temperature of the gas

Kinetic Molecular Theory of Gases • Explaining Observed Behavior with KMT – P and V (T = constant) • • As V is decreased, P increases: V decrease causes a decrease in the surface area. Since P is force/area, the decrease in V causes the area to decrease, thus increasing the P

Kinetic Molecular Theory of Gases – P and T (V = constant) • • As T increase, P increases The increase in T causes an increase in average kinetic energy. Molecules moving faster collide with the walls of the container more frequently, and with greater force.

Kinetic Molecular Theory of Gases – V and T (P = constant) • • As T increases, V also increases Increased T creates more frequent, more forceful collisions. V must increase proportionally to increase the surface area, and maintain P

Kinetic Molecular Theory of Gases – V and n (T and P constant) • • As n increases, V must increase Increasing the number of particles increases the number of collisions. This can be balanced by an increase in V to maintain constant P

Kinetic Molecular Theory of Gases – Dalton’s Law of partial pressures • • P is independent of the type of gas molecule KMT states that particles are independent, and V is assumed to be zero. The identity of the molecule is therefore unimportant

Kinetic Molecular Theory of Gases • Root Mean Square Velocity – Velocity of a gas is dependent on mass and temperature Velocity of gases is determined as an average – • • M = mass of one mole of gas particles in kg R = 8. 3145 J/K • mol – – joule = kg • m 2/s 2 urms = 3 RT M

Kinetic Molecular Theory of Gases • Example: Calculate the root mean square velocity for the atoms in a sample of oxygen gas at 0°C. • MO 2 = 32 g/mol • 32 g 1 kg = 0. 032 kg 1000 g • T = 0 + 273 = 273 K • R = 8. 3145 J/K • mol

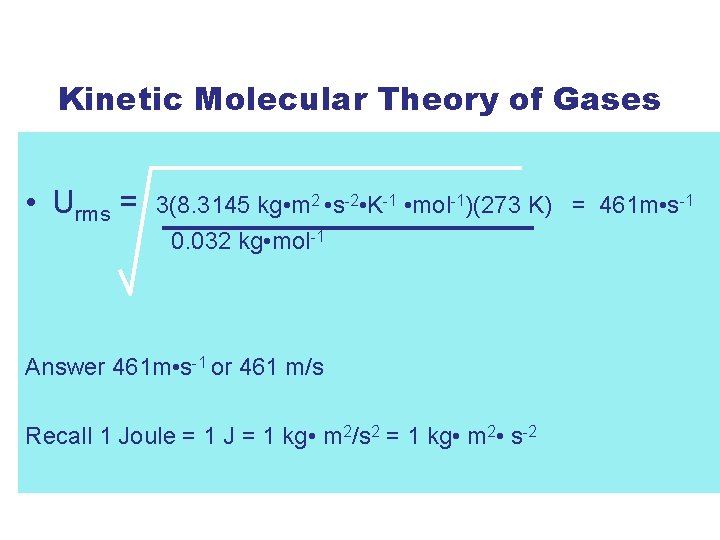
Kinetic Molecular Theory of Gases • Urms = 3(8. 3145 kg • m 2 • s-2 • K-1 • mol-1)(273 K) = 461 m • s-1 0. 032 kg • mol-1 Answer 461 m • s-1 or 461 m/s Recall 1 Joule = 1 J = 1 kg • m 2/s 2 = 1 kg • m 2 • s-2

Kinetic Molecular Theory of Gases • Mean Free Path – distance between collisions – Average distance a molecule travels between collisions • 1 x 10 -7 m for O 2 at STP

Effusion and Diffusion • Effusion – – Movement of a gas through a small opening into an evacuated container (vacuum) Graham’s law of effusion Rate of effusion for gas 1 = √M 2 Rate of effusion for gas 2 √M 1

Effusion and Diffusion • Example: How many times faster than He would NO 2 gas effuse? • MNO 2 = 46. 01 g/mol larger mass • MHe = 4. 003 g/mol effuses slower • Rate He = Rate NO 2 46. 01 4. 003 = He effuses 3. 39 times faster

Real Gases and van der Waals Equation (Johannes van der Waals, 1873) • Volume – – Real gas molecules do have volume Volume available is not 100% of the container volume • • n= number of moles b = is an empirical constant, derived from experimental results

Real Gases and van der Waals Equation • Ideal: P = n. RT V • Real: P = n. RT V-nb

Real Gases and van der Waals Equation • Pressure – Molecules of real gases do experience attractive forces • • a = proportionality constant determined by observation of the gas Pobs = Pideal – a(n/V)2

Real Gases and van der Waals Equation • • Combining to derive van der Waals equation Pobs = n. RT - n 2 a V-nb V 2 And then rearranging… • (Pobs + n 2 a/V 2)(V-nb) = n. RT

Chemistry in the Atmosphere • Composition of the Troposphere – The atmosphere is composed of 78% N 2, 21% O 2, 0. 9%Ar, and 0. 03% CO 2 along with trace gases. – The composition of the atmosphere varies as a function of distance from the earth’s surface. Heavier molecules tend to be near the surface due to gravity.

Chemistry in the Atmosphere – Upper atmospheric chemistry is largely affected by ultraviolet, x ray, and cosmic radiation emanating from space. The ozone layer is especially reactive to ultraviolet radiation – Manufacturing and other processes of our modern society affect the chemistry of our atmosphere. Air pollution is a direct result of such processes.