Forecasting with Regression Models Kafu Wong University of

Forecasting with Regression Models Ka-fu Wong University of Hong Kong 1

Linear regression models Endogenous variable Exogenous variables Explanatory variables Rule, rather than exception: all variables are endogenous. 2

Conditional forecasting The h-step ahead forecast of y given some assumed h-stepahead value of x. T+h. Assumed h-step-ahead value of the exogenous variables Call it scenario analysis or contingency analysis – based on some assumed h-step-ahead value of the exogenous variables. 3

Uncertainty of Forecast n Specification uncertainty / error: our models are only approximation (since no one knows the truth). E. g. , we adopt an AR(1) model but the truth is AR(2). n Almost impossible to account for via a forecast interval. n Parameter uncertainty / sampling error: parameters are estimated from a data sample. The estimate will always be different from the truth. The difference is called sampling error. n Can account for via a forecast interval if we do the calculation carefully. n Innovation uncertainty: errors that cannot be avoided even if we know the true model and true parameter. This is, unavoidable. n Often account for via a forecast interval using standard softwares. 4

Quantifying the innovation and parameter uncertainty Consider the very simple case in which x has a zero mean: 5

Density forecast that accounts for parameter uncertainty ~ 6

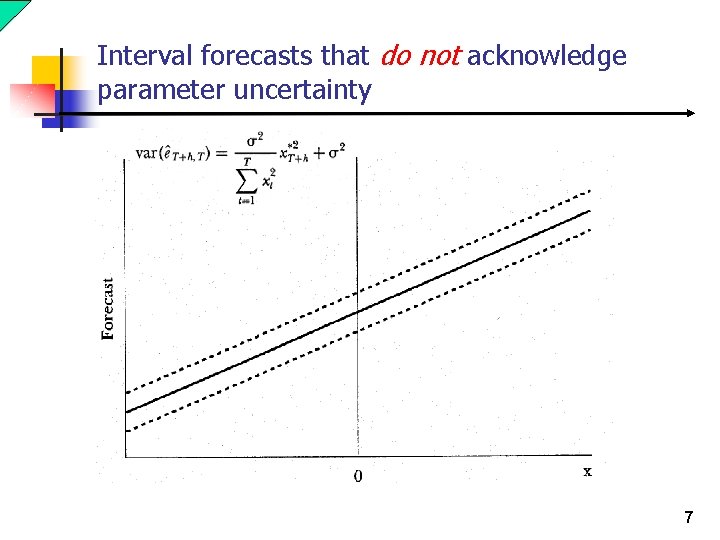
Interval forecasts that do not acknowledge parameter uncertainty 7

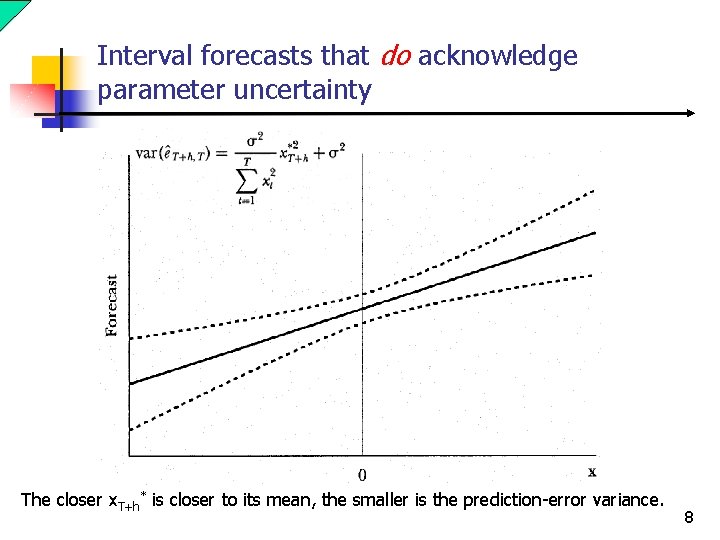
Interval forecasts that do acknowledge parameter uncertainty The closer x. T+h* is closer to its mean, the smaller is the prediction-error variance. 8

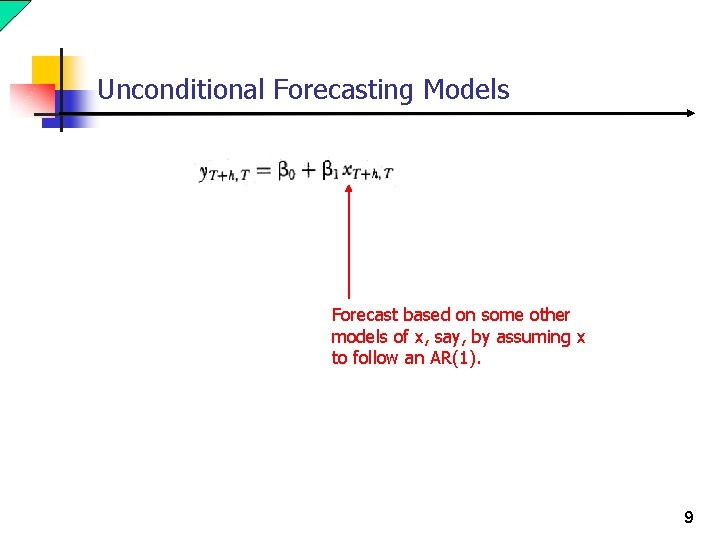
Unconditional Forecasting Models Forecast based on some other models of x, say, by assuming x to follow an AR(1). 9

h-step-ahead forecast without modeling x explicitly Based on unconditional forecasting models n Standing at time T, with observations, (x 1, y 1), (x 2, y 2), …, (x. T, y. T) n 1 -step-ahead: n yt = b 0 + b 1 xt-1 + et n y. T+1 = b 0 + b 1 x. T + et n 2 -step-ahead: n yt = b 0 + b 1 xt-2 + et n y. T+2 = b 0 + b 1 x. T + et n … n h-step-ahead: n yt = b 0 + b 1 xt-h + et n y. T+h = b 0 + b 1 x. T + et 10

h-step-ahead forecast without modeling x explicitly Based on unconditional forecasting models n Special cases: n The model contains only time trends and seasonal components. n Because these components are perfectly predictable. 11

Distributed Lags y depends on a distributed lags of past x’s Parameters to be estimated: b 0, d 1, …, d. Nx 12

Polynomial Distributed Lags Parameters to be estimated: b 0, a, b, c 13

Rational Distributed Lags Example: A(L) = a 0 + a 1 L B(L) = b 0 + b 1 L b 0 yt + b 1 yt-1 = a 0 xt + a 1 xt-1 + b 0 et + b 1 et-1 yt = [- b 1 yt-1 + a 0 xt + a 1 xt-1 + b 0 et + b 1 et-1]/b 0 yt = [- b 1/b 0] yt-1 + [a 0/b 0] xt + [a 1/b 0] xt-1 + et + [b 1/b 0] et-1 14

Regression model with AR(1) disturbance 15

ARMA(p, q) models equivalent to model with only a constant regressor and ARMA(p, q) disturbances. 16

Transfer function models A transfer function is a mathematical representation of the relation between the input and output of a system. 17

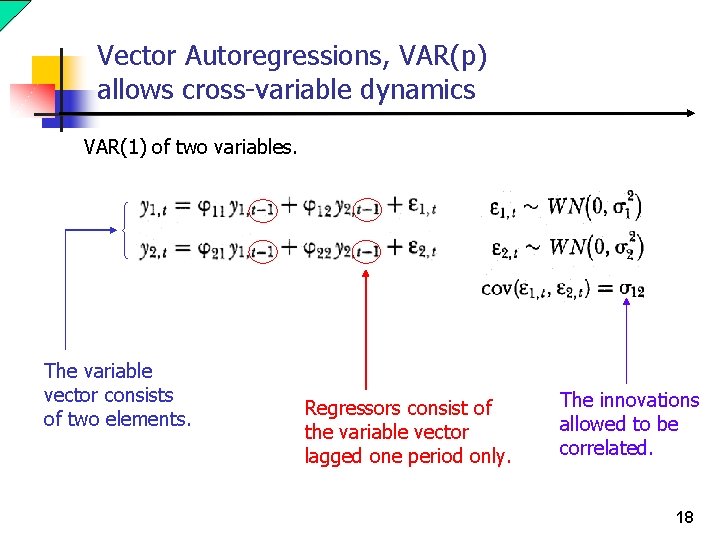
Vector Autoregressions, VAR(p) allows cross-variable dynamics VAR(1) of two variables. The variable vector consists of two elements. Regressors consist of the variable vector lagged one period only. The innovations allowed to be correlated. 18

Estimation of Vector Autoregressions Run OLS regressions equation by equation. OLS estimation turns out to have very good statistical properties when each equation has the same regressors, as in standard VARs. Otherwise, a more complicated estimation procedure called seemingly unrelated regression, which explicitly accounts for correlation across equation disturbances, would be need to obtain estimates with good statistical properties. 19

The choice order Estimation of Vector Autoregressions Use AIC and SIC. 20

Forecast Estimation of Vector Autoregressions Given the parameters, or parameter estimates y 1, T, y 2, T y 1, T+1, Y 2, T+1 y 1, T+1, y 2, T+1 y 1, T+2, Y 2, T+2 y 1, T+2, y 2, T+2 y 1, T+3, Y 2, T+3 y 1, T+3, y 2, T+3 21

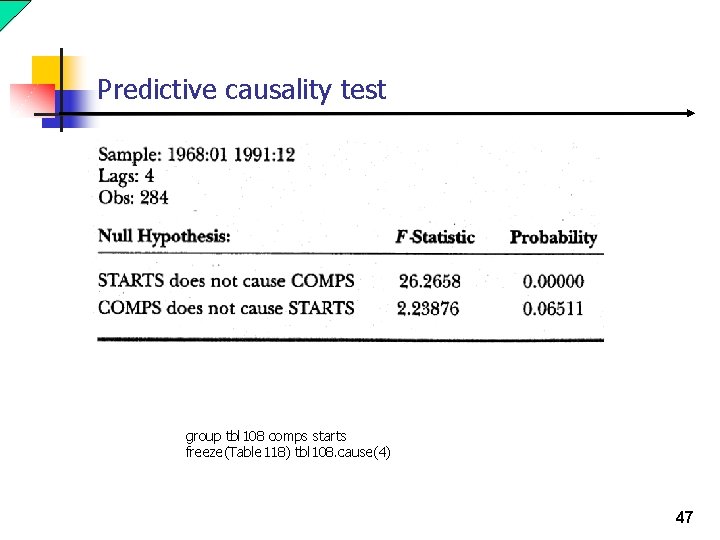
Predictive Causality n Two principles n Cause should occur before effect. n A causal series should contain information useful forecasting that is not available in the other series. n Predictive Causality in a VAR y 2 does not cause y 1 if φ12 =0 In a bivariate VAR, noncausality in 1 -step-ahead forecast will imply noncausality in h-step-ahead forecast. 22

Predictive Causality n In VAR with higher dimension, noncausality in 1 -step-ahead forecast need not imply noncausality in h-step-ahead forecast. n Example: n Variable i may 1 -step-cause variable j n Variable j may 1 -step-cause variable k n Variable i 2 -step-causes variable k but does not 1 -step-cause variable k. 23

Impulse response functions All univariate ARMA(p, q) processes can be written as: We can always normalize the innovations with a constant m: 24

Impulse response functions Impact of et on yt: 1 unit increase in et’ is equivalent to one standard deviation increase in et. 1 unit increase in et’ has b 0’ impact on yt 1 standard deviation increase in et has b 0 s impact on yt, b 1 s impact on yt, etc. 25

AR(1) 26

VAR(1) 27

Normalizing the VAR by the Cholesky factor If y 1 is ordered first, Example: y 1 = GDP, y 2 = Price level An innovation to GDP has effects on current GDP and price level. An innovation to price level has effects only on current price level but not current GDP. 28

Features of Cholesky decomposition n The innovations of the transformed system are in standard deviation units. n The current innovations in the normalized representation have can non-unit coefficients. n The first equation has only one current innovation, e 1, t. The second equation has both current innovations. n The normalization yields a zero covariance between the innovations. 29

Normalizing the VAR by the Cholesky factor If y 2 is ordered first, Example: y 1 = GDP, y 2 = Price level An innovation to price level has effects on current GDP and price level. An innovation to GDP has effects only on current GDP but not current price level. 30

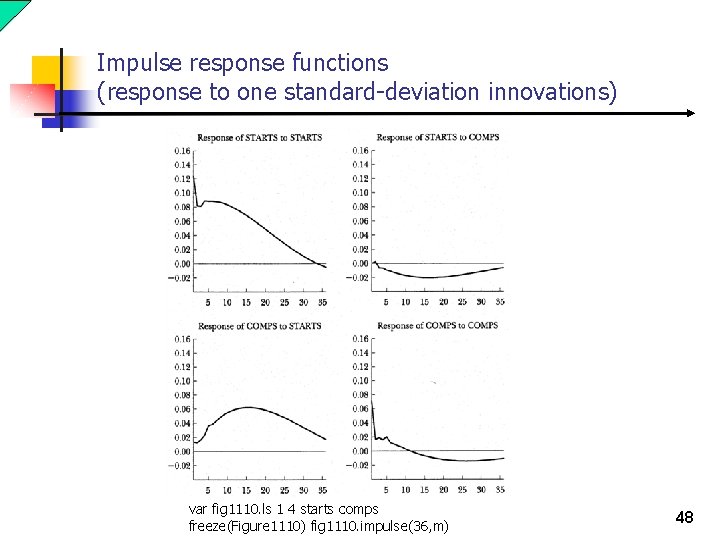
Impulse response functions n With bivariate autoregression, we can compute four sets of impulse -response functions: n y 1 innovations (e 1, t) on y 2 innovations (e 2, t) on y 1 n y 2 innovations (e 2, t) on y 2 31

Variance decomposition n How much of the h-step-ahead forecast error variance of variable i is explained by innovations to variable j, for h=1, 2, …. ? n With bivariate autoregression, we can compute four sets of variance decomposition: n y 1 innovations (e 1, t) on y 2 innovations (e 2, t) on y 1 n y 2 innovations (e 2, t) on y 2 32

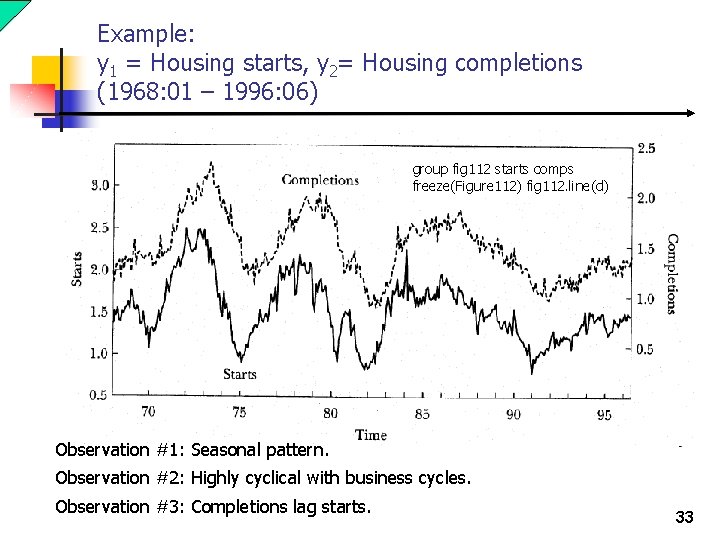
Example: y 1 = Housing starts, y 2= Housing completions (1968: 01 – 1996: 06) group fig 112 starts comps freeze(Figure 112) fig 112. line(d) Observation #1: Seasonal pattern. Observation #2: Highly cyclical with business cycles. Observation #3: Completions lag starts. 33

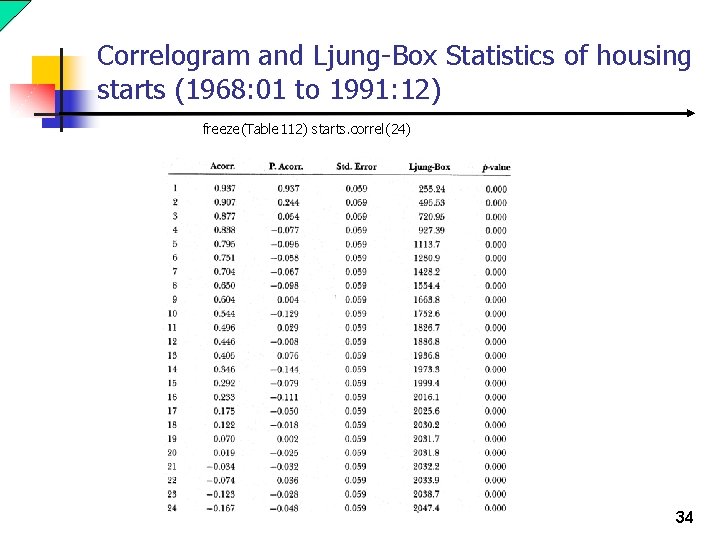
Correlogram and Ljung-Box Statistics of housing starts (1968: 01 to 1991: 12) freeze(Table 112) starts. correl(24) 34

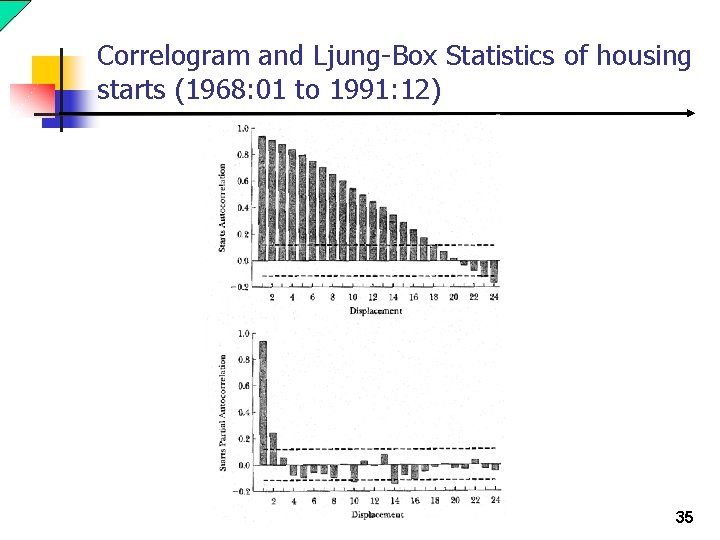
Correlogram and Ljung-Box Statistics of housing starts (1968: 01 to 1991: 12) 35

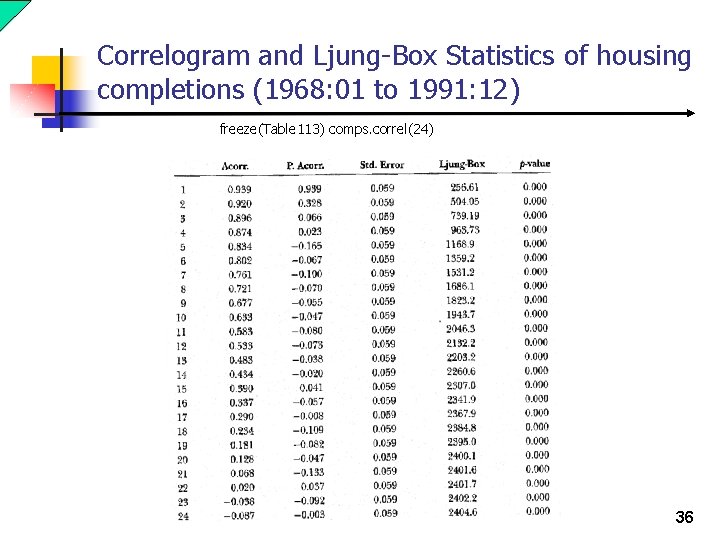
Correlogram and Ljung-Box Statistics of housing completions (1968: 01 to 1991: 12) freeze(Table 113) comps. correl(24) 36

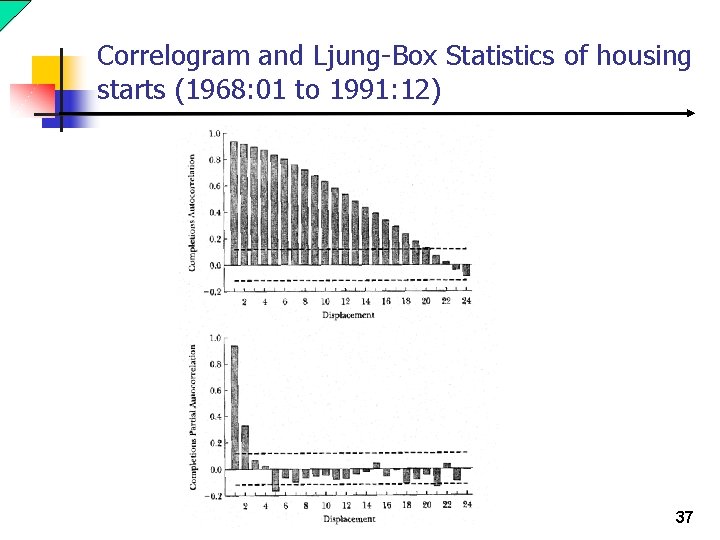
Correlogram and Ljung-Box Statistics of housing starts (1968: 01 to 1991: 12) 37

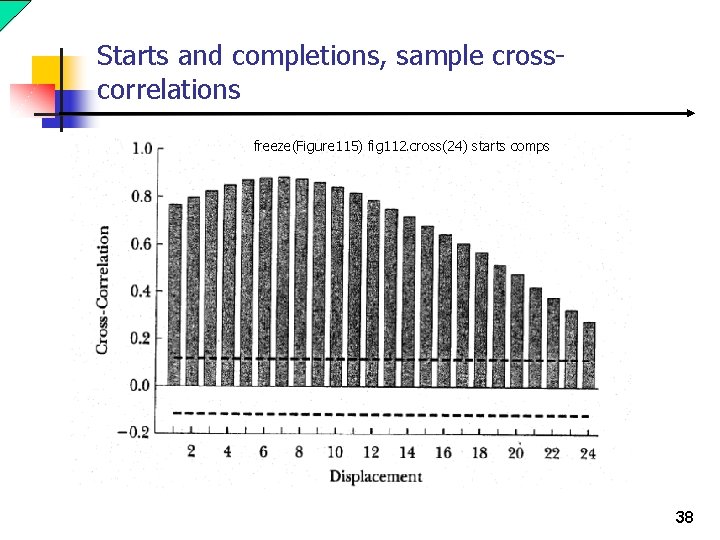
Starts and completions, sample crosscorrelations freeze(Figure 115) fig 112. cross(24) starts comps 38

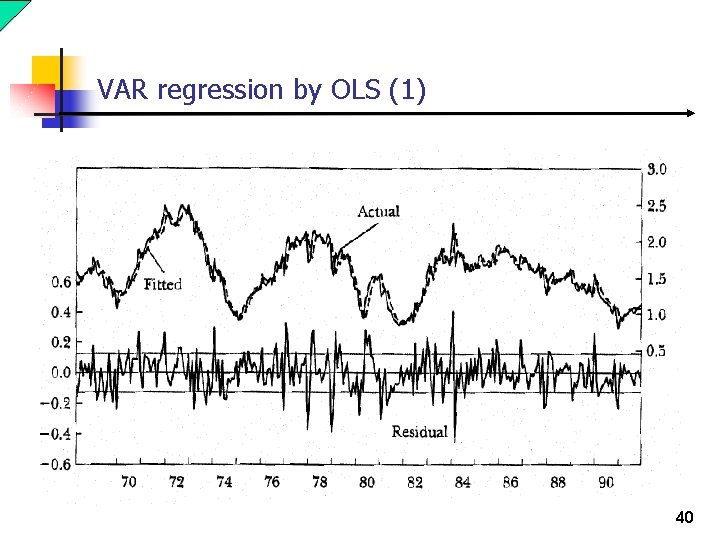
VAR regression by OLS (1) equation Table 114. ls starts c starts(-1) starts(-2) starts(-3) starts(-4) comps(-1) comps(-2) comps(-3) comps(-4) 39

VAR regression by OLS (1) 40

VAR regression by OLS (1) 41

VAR regression by OLS (1) 42

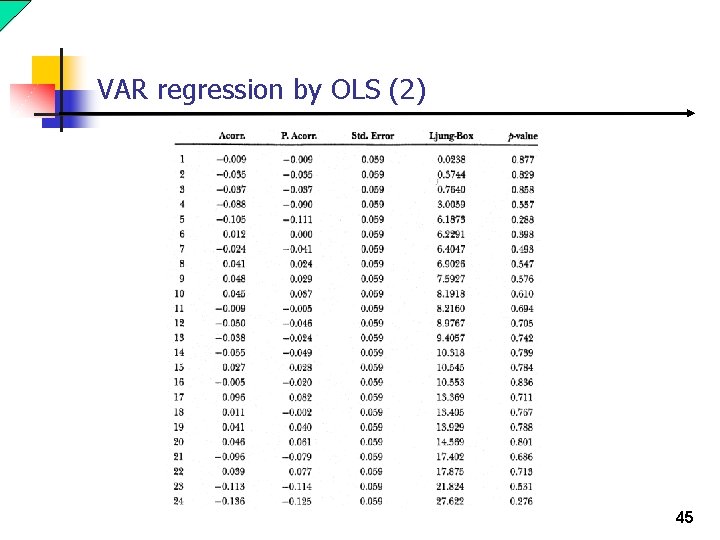
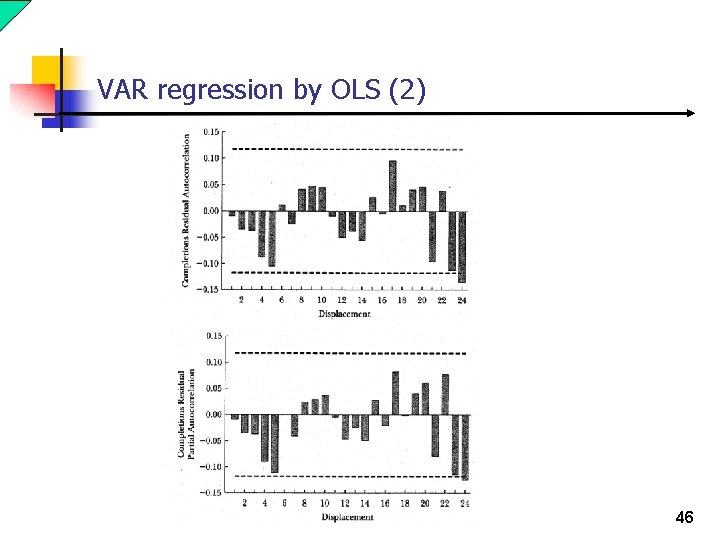
VAR regression by OLS (2) (-4) comps(-1) comps(-2) comps(-3) comps(-4) equation Table 116. ls comps c starts(-1) starts(-2) starts(-3) starts 43

VAR regression by OLS (2) 44

VAR regression by OLS (2) 45

VAR regression by OLS (2) 46

Predictive causality test group tbl 108 comps starts freeze(Table 118) tbl 108. cause(4) 47

Impulse response functions (response to one standard-deviation innovations) var fig 1110. ls 1 4 starts comps freeze(Figure 1110) fig 1110. impulse(36, m) 48

Variance decomposition freeze(Figure 1111) fig 1110. decomp(36, m) 49

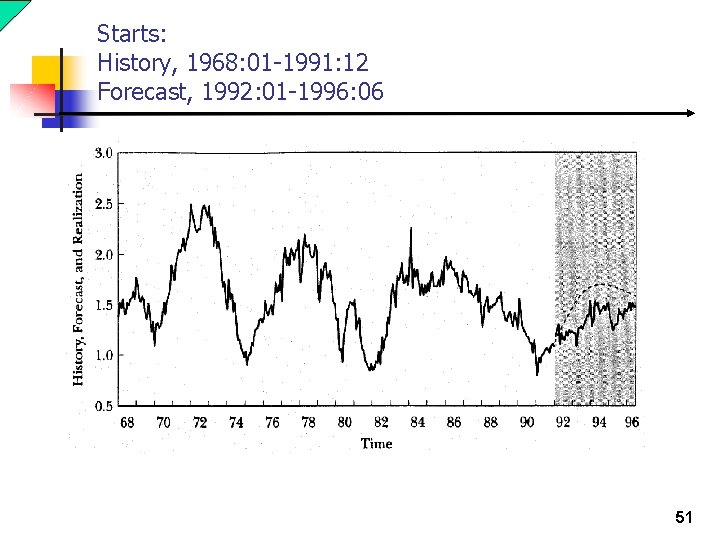
Starts: History, 1968: 01 -1991: 12 Forecast, 1992: 01 -1996: 06 50

Starts: History, 1968: 01 -1991: 12 Forecast, 1992: 01 -1996: 06 51

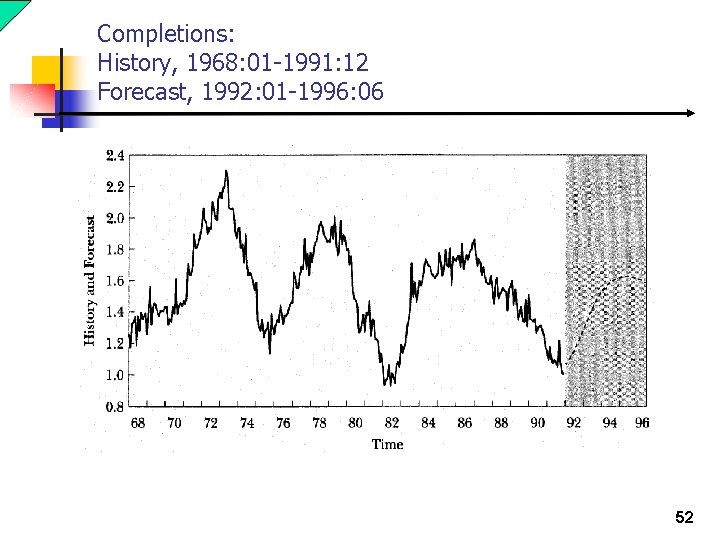
Completions: History, 1968: 01 -1991: 12 Forecast, 1992: 01 -1996: 06 52

Completions: History, 1968: 01 -1991: 12 Forecast, and Realization, 1992: 01 -1996: 06 53

End 54