Dr Kafu Wong ECON 1003 Analysis of Economic

Dr. Ka-fu Wong ECON 1003 Analysis of Economic Data Ka-fu Wong © 2003 Chap 7 - 1

Chapter Seven Estimation and Confidence Intervals GOALS 1. Define a what is meant by a point estimate. 2. Define the term level of confidence. 3. Construct a confidence interval for the population mean when the population standard deviation is known. 4. Construct a confidence interval for the population mean when the population standard deviation is unknown. 5. Construct a confidence interval for the population proportion. 6. Determine the sample size for attribute and variable sampling. l Ka-fu Wong © 2003 Chap 7 - 2

Point and Interval Estimates n A point estimate is a single value (statistic) used to estimate a population value (parameter). n A confidence interval is a range of values within which the population parameter is expected to occur. Ka-fu Wong © 2003 Chap 7 - 3

Confidence Intervals n The degree to which we can rely on the statistic is as important as the initial calculation. Remember, most of the time we are working with samples. And samples give us estimates of the population parameter – only estimates. Ultimately, we are concerned with the accuracy of the estimate. 1. Confidence interval provides range of values n Based on observations from 1 sample 2. Confidence interval gives information about closeness to unknown population parameter n Stated in terms of probability n Exact closeness not known because knowing exact closeness requires knowing unknown population parameter Ka-fu Wong © 2003 Chap 7 - 4

Areas Under the Normal Curve If we draw an observation from the normal distributed population, the drawn value is likely (a chance of 68. 26%) to lie inside the interval of (µ-1σ, µ+1σ). Between: ± 1 - 68. 26% ± 2 - 95. 44% ± 3 - 99. 74% P((µ-1σ <x<µ+1σ) =0. 6826. µ+2σ µ-2σ µ µ-3σ µ-1σ µ+3σ Ka-fu Wong © 2003 Chap 7 - 5

P(µ-1σ <x<µ+1σ) vs P(x-1σ <µ <x+1σ) n P(µ-1σ <x<µ+1σ) is the probability that a drawn observation will lie between (µ-1σ, µ+1σ). P(µ-1σ <x<µ+1σ) = P(µ-1σ -µ-x <x -µ-x<µ +1σ -µ-x) = P(-1σ -x <-µ<1σ -x) = P(-(-1σ -x )>-(-µ)>-(1σ -x)) = P(1σ +x >µ>-1σ +x) = P(x - 1σ <µ <x+1σ) n P(x-1σ <µ <x+1σ) is the probability that the population mean will lie between (x-1σ, x+1σ). Ka-fu Wong © 2003 Chap 7 - 6

P(µ-1σm <x<µ+1 σm) vs P(m-1 σm <µ <m+1 σm) (m=sample mean) n P(µ-1 σm <m<µ+1 σm) is the probability that a drawn observation will lie between (µ-1σ, µ+1σ). P(µ-1 σm <m<µ+1 σm) = P(µ-1 σm -µ-m <x -µ-m<µ +1 σm -µ-m) = P(-1 σm -m <-µ<1 σm -m) = P(-(-1 σm -m )>-(-µ)>-(1 σm -m)) = P(1 σm +m>µ>-1 σm +m) = P(m - 1 σm <µ <m+1 σm) n P(m-1 σm <µ <m+1 σm) is the probability that the population mean will lie between (m-1 σm , m+1 σm). Ka-fu Wong © 2003 Chap 7 - 7

P(µ-a <x<µ+b) vs P(x-a<µ <x+b) n P(µ-a <x<µ+b) is the probability that a drawn observation will lie between (µ-a, µ+b). n P(x-a <µ <x+b) is the probability that the population mean will lie between (x - a, x+ b). NO!!!! n Generally, P(µ-a <x<µ+b) = P(x-a <µ <x+b) n Generally, P(µ-a <x<µ+b) and P(x-a <µ <x+b) are not equal. They are equal only if a = b. That is, when the confidence interval is symmetric. Ka-fu Wong © 2003 Chap 7 - 8

P(µ-a <x<µ+b) = P(x-b <µ <x+a) n P(µ-a <x<µ+b) is the probability that a drawn observation will lie between (µ-a, µ+b). P(µ-a <x<µ+b) = P(µ-a -µ-x <x -µ-x<µ +b -µ-x) = P(-a -x <-µ<b -x) = P(-(-a -x )>-(-µ)>-(b -x)) = P(a +x >µ>-b +x) = P(x - b <µ <x+a) n P(x-b <µ <x+a) is the probability that the population mean will lie between (x - b, x+ a). Ka-fu Wong © 2003 Chap 7 - 9

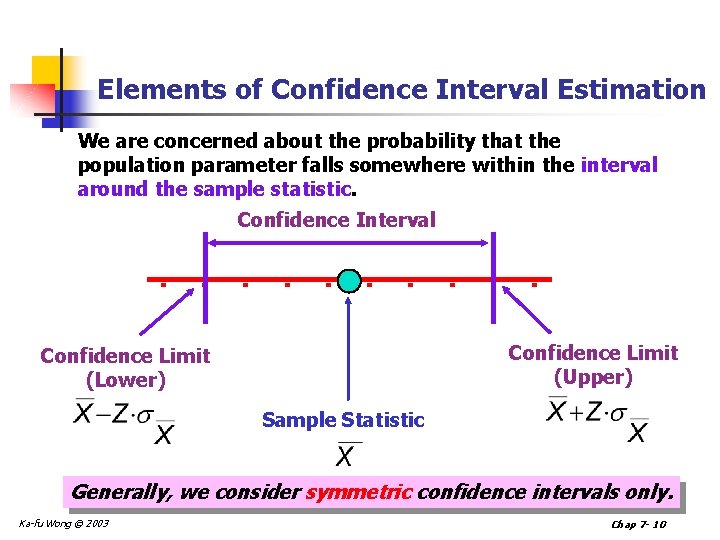
Elements of Confidence Interval Estimation We are concerned about the probability that the population parameter falls somewhere within the interval around the sample statistic. Confidence Interval Confidence Limit (Upper) Confidence Limit (Lower) Sample Statistic Generally, we consider symmetric confidence intervals only. Ka-fu Wong © 2003 Chap 7 - 10

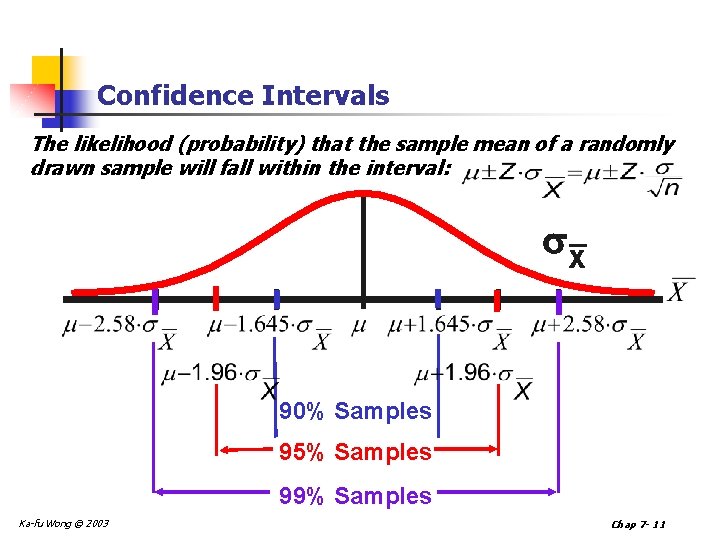
Confidence Intervals The likelihood (probability) that the sample mean of a randomly drawn sample will fall within the interval: x_ 90% Samples 95% Samples 99% Samples Ka-fu Wong © 2003 Chap 7 - 11

Confidence Intervals The likelihood (or probability) that the sample mean will fall within “ 1 standard deviation” of the population mean is the same as the likelihood (or probability) that the population mean will fall within “ 1 standard deviation” of the sample mean. Z 1. 645 0. 90 1. 96 0. 95 2. 58 0. 99 Ka-fu Wong © 2003 Chap 7 - 12

Level of Confidence 1. Probability that the unknown population parameter falls within the interval 2. Denoted (1 - = level of confidence n is the probability that the parameter is not within the interval 3. Typical values are 99%, 95%, 90% Ka-fu Wong © 2003 Chap 7 - 13

Interpreting Confidence Intervals n Once a confidence interval has been constructed, it will either contain the population mean or it will not. n For a (1 - ) 95% confidence interval, n If we were to draw 1000 samples and construct the (1 - ) confidence interval for the population mean for 95% each of the 1000 samples. n Some of the intervals contain the population mean, some not. n If the interval is a (1 - ) 95% confidence interval, about 950 of the confidence intervals will contain the population mean. n That is, (1 - ) 95% of the samples will contain the population mean. Ka-fu Wong © 2003 Chap 7 - 14

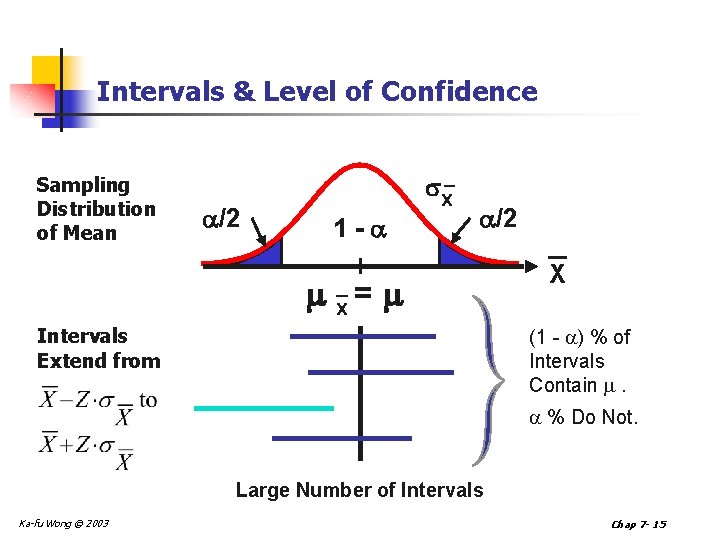
Intervals & Level of Confidence Sampling Distribution of Mean _ /2 x 1 - /2 x = Intervals Extend from _ X (1 - ) % of Intervals Contain . % Do Not. Large Number of Intervals Ka-fu Wong © 2003 Chap 7 - 15

Point Estimates and Interval Estimates n The factors that determine the width of a confidence interval are: 1. The size of the sample (n) from which the statistic is calculated. 2. The variability in the population, usually estimated by s. 3. The desired level of confidence. _ /2 Ka-fu Wong © 2003 x 1 - = /2 _ X Chap 7 - 16

Point and Interval Estimates n We may use the z distribution if one of the following conditions hold: n The population is normal and its standard deviation is known n The sample has more than 30 observations (The population standard deviation can be known or unknown). n Technical note: n If the random variables A and B are normally distributed, Y = A+B and X=(A+B)/2 will be normally distributed. n If the population is normal, the sample mean of a random sample of n observations (for any integer n) will Ka-fu Wong © 2003 be normally distributed. Chap 7 - 17

Point and Interval Estimates n Use the t distribution if all of the following conditions are fulfilled: n The population is normal n The population standard deviation is unknown and the sample has less than 30 observations. n Note that the t distribution does not cover those nonnormal populations. Ka-fu Wong © 2003 Chap 7 - 18

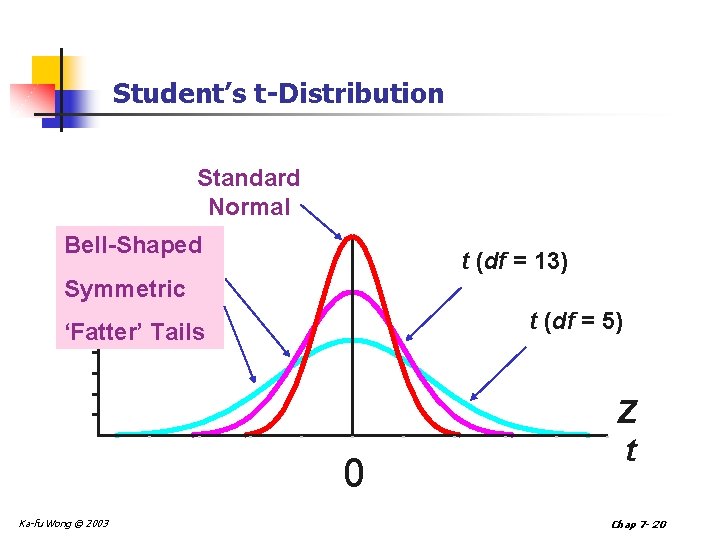
Student’s t-Distribution n The t-distribution is a family of distributions that is bellshaped and symmetric like the standard normal distribution but with greater area in the tails. Each distribution in the t-family is defined by its degrees of freedom. As the degrees of freedom increase, the tdistribution approaches the normal distribution. n Student is a pen name for a statistician named William S. Gosset who was not allowed to publish under his real name. Gosset assumed the pseudonym Student for this purpose. Student’s t distribution is not meant to reference anything regarding college students. Ka-fu Wong © 2003 Chap 7 - 19

Student’s t-Distribution Standard Normal Bell-Shaped t (df = 13) Symmetric t (df = 5) ‘Fatter’ Tails 0 Ka-fu Wong © 2003 Z t Chap 7 - 20

Student’s t Table Upper Tail Area df . 25 . 10 . 05 /2 Assume: n=3 df = n - 1 = 2 =. 10 /2 =. 05 1 1. 000 3. 078 6. 314 2 0. 817 1. 886 2. 920 . 05 3 0. 765 1. 638 2. 353 t Values Ka-fu Wong © 2003 0 2. 920 t Chap 7 - 21

Degrees of freedom (df) n Degrees of freedom refers to the number of independent data values available to estimate the population’s standard deviation. If k parameters must be estimated before the population’s standard deviation can be calculated from a sample of size n, the degrees of freedom are equal to n - k. n Example Sum of 3 numbers is 6 X 1 = 1 (or Any Number) X 2 = 2 (or Any Number) X 3 = 3 (Cannot Vary) Sum = 6 Ka-fu Wong © 2003 Degrees of freedom = n -1 = 3 -1 =2 Chap 7 - 22

t-Values where: = Sample mean = Population mean s = Sample standard deviation n = Sample size Ka-fu Wong © 2003 Chap 7 - 23

Confidence interval for mean ( unknown in small sample) A random sample of n = 25 has = 50 and S = 8. Set up a 95% confidence interval estimate for . X t / 2, n 1 50 2. 0639 S n 8 X t / 2, n 1 50 2. 0639 25 46. 69 53. 30 Ka-fu Wong © 2003 S n 8 25 Chap 7 - 24

Central Limit Theorem n For a population with a mean and a variance 2 the sampling distribution of the means of all possible samples of size n generated from the population will be approximately normally distributed. n The mean of the sampling distribution equal to and the variance equal to 2/n. The population distribution The sample mean of n observation Ka-fu Wong © 2003 Chap 7 - 25

Standard Error of the Sample Means n The standard error of the sample mean is the standard deviation of the sampling distribution of the sample means. n It is computed by is the symbol for the standard error of the sample mean. n σ is the standard deviation of the population. n n is the size of the sample. n Ka-fu Wong © 2003 Chap 7 - 26

Standard Error of the Sample Means n If is not known and n 30, the standard deviation of the sample, designated s, is used to approximate the population standard deviation. The formula for the standard error is: Ka-fu Wong © 2003 Chap 7 - 27

95% and 99% Confidence Intervals for the sample mean n The 95% and 99% confidence intervals are constructed as follows: n 95% CI for the sample mean is given by n 99% CI for the sample mean is given by Ka-fu Wong © 2003 Chap 7 - 28

95% and 99% Confidence Intervals for µ n The 95% and 99% confidence intervals are constructed as follows: n 95% CI for the population mean is given by n 99% CI for the population mean is given by Ka-fu Wong © 2003 Chap 7 - 29

Constructing General Confidence Intervals for µ n In general, a confidence interval for the mean is computed by: Ka-fu Wong © 2003 Chap 7 - 30

EXAMPLE 3 n The Dean of the Business School wants to estimate the mean number of hours worked per week by students. A sample of 49 students showed a mean of 24 hours with a standard deviation of 4 hours. What is the population mean? n The value of the population mean is not known. Our best estimate of this value is the sample mean of 24. 0 hours. This value is called a point estimate. Ka-fu Wong © 2003 Chap 7 - 31

Example 3 continued Find the 95 percent confidence interval for the population mean. The confidence limits range from 22. 88 to 25. 12. About 95 percent of the similarly constructed intervals include the population parameter. Ka-fu Wong © 2003 Chap 7 - 32

Confidence Interval for a Population Proportion n The confidence interval for a population proportion is estimated by: Ka-fu Wong © 2003 Chap 7 - 33

EXAMPLE 4 n A sample of 500 executives who own their own home revealed 175 planned to sell their homes and retire to Arizona. Develop a 98% confidence interval for the proportion of executives that plan to sell and move to Arizona. Ka-fu Wong © 2003 Chap 7 - 34

Finite-Population Correction Factor n A population that has a fixed upper bound is said to be finite. n For a finite population, where the total number of objects is N and the size of the sample is n, the following adjustment is made to the standard errors of the sample means and the proportion: n Standard error of the sample means when is known: n Standard error of the sample means when is NOT known and need to be estimated by s: Ka-fu Wong © 2003 Chap 7 - 35

Finite-Population Correction Factor n Standard error of the sample proportions: n This adjustment is called the finite-population correction factor. n If n/N <. 05, the finite-population correction factor is ignored. Ka-fu Wong © 2003 Chap 7 - 36

EXAMPLE 5 n Given the information in EXAMPLE 3, construct a 95% confidence interval for the mean number of hours worked per week by the students if there are only 500 students on campus. n Because n/N = 49/500 =. 098 which is greater than 05, we use the finite population correction factor. Ka-fu Wong © 2003 Chap 7 - 37

Selecting a Sample Size n There are 3 factors that determine the size of a sample, none of which has any direct relationship to the size of the population. They are: n The degree of confidence selected. n The maximum allowable error. n The variation in the population. Ka-fu Wong © 2003 Chap 7 - 38

Selecting a Sample Size n To find the sample size for a variable: where : E is the allowable error, z is the z- value corresponding to the selected level of confidence, and s is the sample deviation of the pilot survey. Ka-fu Wong © 2003 Chap 7 - 39

EXAMPLE 6 n A consumer group would like to estimate the mean monthly electricity charge for a single family house in July within $5 using a 99 percent level of confidence. Based on similar studies the standard deviation is estimated to be $20. 00. How large a sample is required? Ka-fu Wong © 2003 Chap 7 - 40

Sample Size for Proportions n The formula for determining the sample size in the case of a proportion is: n where p is the estimated proportion, based on past experience or a pilot survey; z is the z value associated with the degree of confidence selected; E is the maximum allowable error the researcher will tolerate. Ka-fu Wong © 2003 Chap 7 - 41

EXAMPLE 7 n The American Kennel Club wanted to estimate the proportion of children that have a dog as a pet. If the club wanted the estimate to be within 3% of the population proportion, how many children would they need to contact? Assume a 95% level of confidence and that the club estimated that 30% of the children have a dog as a pet. Ka-fu Wong © 2003 Chap 7 - 42

Summary: Confidence interval for sample mean General confidence interval: (m = population mean; = confidence level; s = standard deviation) s unknown s known Sample Size (n) <30 Population distribution Normal Unknown ? ≥ 30 Ka-fu Wong © 2003 Chap 7 - 43

Summary: Confidence Interval for sample proportion General confidence interval: (p= population mean; = confidence level; s = standard deviation) s known Sample Size (n) Population distribution Normal Unknown s unknown Population distribution Normal Unknown <30 ≥ 30 Because s = p(1 -p), we know s if only if we know p. If we know p, there is no need to estimate p or to construct the confidence interval for p. Ka-fu Wong © 2003 Chap 7 - 44

Chapter Seven Estimation and Confidence Intervals - END - Ka-fu Wong © 2003 Chap 7 - 45