First Order Logic CS 171 Fall 2016 Introduction
































































![Prolog • Appending two lists to produce a third: append([], Y, Y). append([X|L], Y, Prolog • Appending two lists to produce a third: append([], Y, Y). append([X|L], Y,](https://slidetodoc.com/presentation_image/e0a4842605f17b7f5ecc25a7a3f7bd14/image-80.jpg)






- Slides: 88

First Order Logic CS 171, Fall 2016 Introduction to Artificial Intelligence Prof. Alexander Ihler

Outline • New ontology – objects, relations, properties, functions. • New Syntax – Constants, predicates, properties, functions • New semantics – meaning of new syntax • Inference rules for Predicate Logic (FOL) – Resolution – Forward-chaining, Backward-chaining – Unification • Reading: Russell and Norvig Chapters 8 & 9


Building a more expressive language Want to develop a better, more expressive language: • Needs to refer to objects in the world, • Needs to express general rules – – – On(x, y) ~ clear(y) All men are mortal Everyone over age 21 can drink One student in this class got a perfect score Etc…. • First order logic, or “predicate calculus” allows more expressiveness






Semantics: Worlds • The world consists of objects that have properties. – There are relations and functions between these objects – Objects in the world, individuals: people, houses, numbers, colors, baseball games, wars, centuries • Clock A, John, 7, the-house in the corner, Tel-Aviv – Functions on individuals: • father-of, best friend, third inning of, one more than – Relations: • brother-of, bigger than, inside, part-of, has color, occurred after – Properties (a relation of arity 1): • red, round, bogus, prime, multistoried, beautiful

Semantics: Interpretation • An interpretation of a sentence (wff) is an assignment that maps – Object constants to objects in the worlds, – n-ary function symbols to n-ary functions in the world, – n-ary relation symbols to n-ary relations in the world • Given an interpretation, an atom has the value “true” if it denotes a relation that holds for those individuals denoted in the terms. Otherwise it has the value “false” – Example: Block world: • A, B, C, floor, On, Clear – World: – On(A, B) is false, Clear(B) is true, On(C, F 1) is true…


Truth in first-order logic • Sentences are true with respect to a model and an interpretation • Model contains objects (domain elements) and relations among them • Interpretation specifies referents for constant symbols → objects predicate symbols → relations function symbols → functional relations • An atomic sentence predicate(term 1, . . . , termn) is true iff the objects referred to by term 1, . . . , termn are in the relation referred to by predicate

Semantics: Models • An interpretation satisfies a wff (sentence) if the wff has the value “true” under the interpretation. • Model: An interpretation that satisfies a wff is a model of that wff • Validity: Any wff that has the value “true” under all interpretations is valid • Any wff that does not have a model is inconsistent or unsatisfiable • If a wff w has a value true under all the models of a set of sentences KB then KB logically entails w

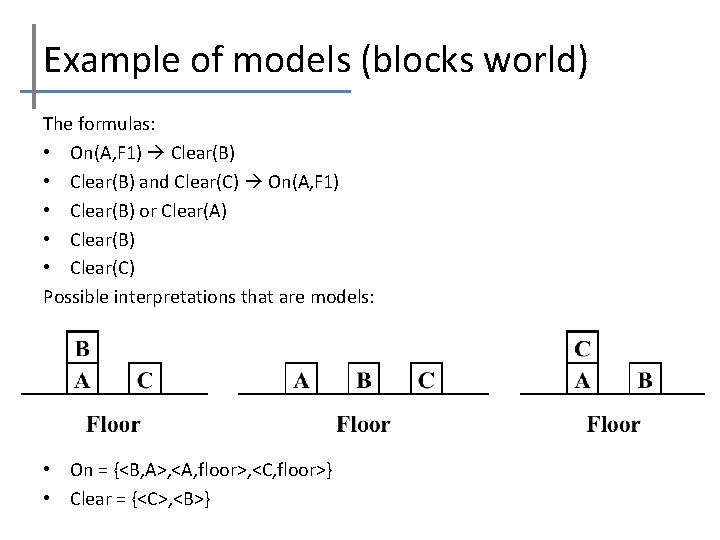
Example of models (blocks world) The formulas: • On(A, F 1) Clear(B) • Clear(B) and Clear(C) On(A, F 1) • Clear(B) or Clear(A) • Clear(B) • Clear(C) Possible interpretations that are models: • On = {<B, A>, <A, floor>, <C, floor>} • Clear = {<C>, <B>}


Quantification • Universal and existential quantifiers allow expressing general rules with variables • Universal quantification – All cats are mammals – It is equivalent to the conjunction of all the sentences obtained by substitution the name of an object for the variable x. • Syntax: if w is a wff then (forall x) w is a wff.

Quantification: Universal • Universal quantification 8 : a universally quantified sentence is true if it is true for every object in the model Everyone in Irvine has a tan: • Roughly equivalent to conjunction:

A common mistake • Typically, “implies” = “)” is the main connective operator with 8 • Everyone in Irvine has a tan: 8 x : In. Irvine(x) ) Tan(x) • Operator Æ is uncommon 8 x : In. Irvine(x) Æ Tan(x) means that everyone lives in Irvine and is tan.

Quantification: Existential • Existential quantification : an existentially quantified sentence is true in case one of the disjunct is true Spot has a sister who is a cat: • Roughly quivalent to disjunction: • We can mix existential and universal quantification.

A common mistake • Typically, “and” = “Æ” is the main connective operator with 9 • Spot has a sister who is a cat: 9 x : Sister(x, Spot) Æ Cat(x) • Operator ) is uncommon 9 x : Sister(x, Spot) ) Cat(x) is true if there is anyone who is not Spot’s sister

Properties of quantifiers • x y is the same as y x • x y is not the same as y x • x y Loves(x, y) – “There is a person who loves everyone in the world” • y x Loves(x, y) – “Everyone in the world is loved by at least one person” • Quantifier duality: each can be expressed using the other x Likes(x, Ice. Cream) x Likes(x, Broccoli)





Equality • term 1 = term 2 is true under a given interpretation if and only if term 1 and term 2 refer to the same object • E. g. , definition of Sibling in terms of Parent: x, y Sibling(x, y) [ (x = y) m, f (m = f) Parent(m, x) Parent(f, x) Parent(m, y) Parent(f, y)]

Using FOL • The kinship domain: – object are people – Properties include gender and they are related by relations such as parenthood, brotherhood, marriage – predicates: Male, Female (unary) Parent, Sibling, Daughter, Son. . . – Function: Mother Father • Brothers are siblings – x, y Brother(x, y) Sibling(x, y) • One's mother is one's female parent – m, c Mother(c) = m (Female(m) Parent(m, c)) • “Sibling” is symmetric – x, y Sibling(x, y) Sibling(y, x)

Using FOL • • • The set domain: s Set(s) (s = {} ) ( x, s 2 Set(s 2) s = {x|s 2}) x, s {x|s} = {} (Adjoining an element already in the set has no effect) x, s x s s = {x|s} (the only members of a set are the elements that were adjoint into it) x, s x s [ y, s 2} (s = {y|s 2} (x = y x s 2))] s 1, s 2 s 1 s 2 ( x x s 1 x s 2) s 1, s 2 (s 1 = s 2) (s 1 s 2 s 1) x, s 1, s 2 x (s 1 s 2) (x s 1 x s 2) Objects are sets Predicates: unary predicate “set: , binary predicate membership (x is a member of set), “subset” (s 1 is a subset of s 2) Functions: intersections, union, adjoining an eleiment to a set.

Knowledge engineering in FOL • Identify the task • Assemble the relevant knowledge • Decide on a vocabulary of predicates, functions, and constants • Encode general knowledge about the domain • Encode a description of the specific problem instance • Pose queries to the inference procedure and get answers • Debug the knowledge base

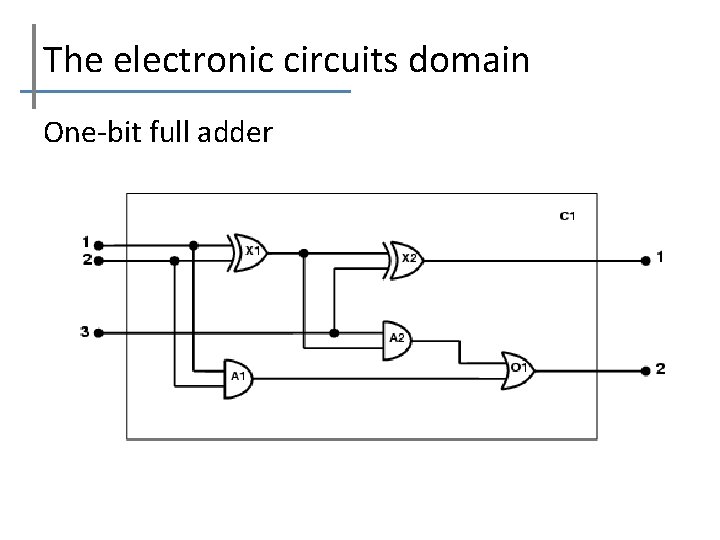
The electronic circuits domain One-bit full adder

The electronic circuits domain • Identify the task – Does the circuit actually add properly? (circuit verification) • Assemble the relevant knowledge – Composed of wires and gates; Types of gates (AND, OR, XOR, NOT) – Irrelevant: size, shape, color, cost of gates • Decide on a vocabulary – Alternatives: • Type(X 1) = XOR • Type(X 1, XOR) • XOR(X 1)

The electronic circuits domain • Encode general knowledge of the domain – t 1, t 2 Connected(t 1, t 2) Signal(t 1) = Signal(t 2) – t Signal(t) = 1 Signal(t) = 0 – 1≠ 0 – t 1, t 2 Connected(t 1, t 2) Connected(t 2, t 1) – – g Type(g) = OR Signal(Out(1, g)) = 1 n Signal(In(n, g)) = 1 g Type(g) = AND Signal(Out(1, g)) = 0 n Signal(In(n, g)) = 0 g Type(g) = XOR Signal(Out(1, g)) = 1 Signal(In(1, g)) ≠ Signal(In(2, g)) g Type(g) = NOT Signal(Out(1, g)) ≠ Signal(In(1, g))

The electronic circuits domain • Encode the specific problem instance – Type(X 1) = XOR – Type(A 1) = AND – Type(O 1) = OR – – – Type(X 2) = XOR Type(A 2) = AND Connected(Out(1, X 1), In(1, X 2)) Connected(Out(1, X 1), In(2, A 2)) Connected(Out(1, A 2), In(1, O 1)) Connected(Out(1, A 1), In(2, O 1)) Connected(Out(1, X 2), Out(1, C 1)) Connected(Out(1, O 1), Out(2, C 1)) Connected(In(1, C 1), In(1, X 1)) Connected(In(1, C 1), In(1, A 1)) Connected(In(2, C 1), In(2, X 1)) Connected(In(2, C 1), In(2, A 1)) Connected(In(3, C 1), In(2, X 2)) Connected(In(3, C 1), In(1, A 2))

The electronic circuits domain 6. Pose queries to the inference procedure What are the possible sets of values of all the terminals for the adder circuit? i 1, i 2, i 3, o 1, o 2 Signal(In(1, C_1)) = i 1 Signal(In(2, C 1)) = i 2 Signal(In(3, C 1)) = i 3 Signal(Out(1, C 1)) = o 1 Signal(Out(2, C 1)) = o 2 • Debug the knowledge base (May have omitted assertions like 1 ≠ 0)







Some more notation • Instantiation: specify values for variables • Ground term – A term without variables • Substitution – Setting a variable equal to something – q = {x / John, y / Richard} – Read as “x : = John, y: =Richard” • Write a subsitution into sentence a as Subst(q, a) or just as aq

Universal instantiation (UI) • Every instantiation of a universally quantified sentence is entailed by it: v α Subst({v/g}, α) for any variable v and ground term g • E. g. , x King(x) Greedy(x) Evil(x) yields: King(John) Greedy(John) Evil(John) King(Richard) Greedy(Richard) Evil(Richard) King(Father(John)) Greedy(Father(John)) Evil(Father(John)). . .

Existential instantiation (EI) • For any sentence α, variable v, and constant symbol k that does not appear elsewhere in the knowledge base: v α Subst({v/k}, α) • E. g. , x Crown(x) On. Head(x, John) yields: Crown(C 1) On. Head(C 1, John) provided C 1 is a new constant symbol, called a Skolem constant

Reduction to propositional inference Suppose the KB contains just the following: x King(x) Greedy(x) Evil(x) King(John) Greedy(John) Brother(Richard, John) • Instantiating the universal sentence in all possible ways, we have: • The new KB is propositionalized: proposition symbols are King(John) Greedy(John) Evil(John) King(Richard) Greedy(Richard) Evil(Richard) King(John) Greedy(John) Brother(Richard, John) King(John), Greedy(John), Evil(John), King(Richard), etc.

Reduction contd. • Every FOL KB can be propositionalized so as to preserve entailment • (A ground sentence is entailed by new KB iff entailed by original KB) • Idea: propositionalize KB and query, apply resolution, return result • Problem: with function symbols, there are infinitely many ground terms, – e. g. , Father(Father(John)))

Reduction contd. Theorem: Herbrand (1930). If a sentence α is entailed by an FOL KB, it is entailed by a finite subset of the propositionalized KB Idea: For n = 0 to ∞ do create a propositional KB by instantiating with depth-$n$ terms see if α is entailed by this KB Problem: works if α is entailed, loops if α is not entailed Theorem: Turing (1936), Church (1936) Entailment for FOL is semidecidable (algorithms exist that say yes to every entailed sentence, but no algorithm exists that also says no to every nonentailed sentence. )

Problems with propositionalization • Propositionalization seems to generate lots of irrelevant sentences. • E. g. , from: x King(x) Greedy(x) Evil(x) King(John) y Greedy(y) Brother(Richard, John) • Given query “evil(x) it seems obvious that Evil(John), but propositionalization produces lots of facts such as Greedy(Richard) that are irrelevant • With p k-ary predicates and n constants, there are p·nk instantiations.

Generalized Modus Ponens (GMP) p 1', p 2', … , pn', ( p 1 p 2 … pn q) qθ p 1' is King(John) p 1 is King(x) p 2' is Greedy(y) p 2 is Greedy(x) θ is {x/John, y/John} q is Evil(x) q θ is Evil(John) where pi'θ = pi θ for all i • GMP used with KB of definite clauses (exactly one positive literal) • All variables assumed universally quantified

Soundness of GMP • Need to show that p 1', …, pn', (p 1 … pn q) ╞ qθ provided that pi'θ = piθ for all I • Lemma: For any sentence p, we have p ╞ pθ by UI – (p 1 … pn q) ╞ (p 1 … pn q)θ = (p 1θ … pnθ qθ) – p 1', ; …, ; pn' ╞ p 1' … pn' ╞ p 1'θ … pn'θ – From 1 and 2, qθ follows by ordinary Modus Ponens

Unification • We can get the inference immediately if we can find a substitution θ such that King(x) and Greedy(x) match King(John) and Greedy(y) θ = {x/John, y/John} works • Unify(α, β) = θ if αθ = βθ p Knows(John, x) q Knows(John, Jane) Knows(y, OJ) Knows(y, Mother(y)) Knows(x, OJ) θ {x/Jane}} {x/OJ, y/John}} {y/John, x/Mother(John)}} {fail} • Standardizing apart eliminates overlap of variables, e. g. , Knows(z 17, OJ)

Unification • We can get the inference immediately if we can find a substitution θ such that King(x) and Greedy(x) match King(John) and Greedy(y) θ = {x/John, y/John} works • Unify(α, β) = θ if αθ = βθ p Knows(John, x) q Knows(John, Jane) Knows(y, OJ) Knows(y, Mother(y)) Knows(x, OJ) θ {x/Jane}} {x/OJ, y/John}} {y/John, x/Mother(John)}} {fail} • Standardizing apart eliminates overlap of variables, e. g. , Knows(z 17, OJ)

Unification • We can get the inference immediately if we can find a substitution θ such that King(x) and Greedy(x) match King(John) and Greedy(y) θ = {x/John, y/John} works • Unify(α, β) = θ if αθ = βθ p Knows(John, x) q Knows(John, Jane) Knows(y, OJ) Knows(y, Mother(y)) Knows(x, OJ) θ {x/Jane}} {x/OJ, y/John}} {y/John, x/Mother(John)}} {fail} • Standardizing apart eliminates overlap of variables, e. g. , Knows(z 17, OJ)

Unification • We can get the inference immediately if we can find a substitution θ such that King(x) and Greedy(x) match King(John) and Greedy(y) θ = {x/John, y/John} works • Unify(α, β) = θ if αθ = βθ p Knows(John, x) q Knows(John, Jane) Knows(y, OJ) Knows(y, Mother(y)) Knows(x, OJ) θ {x/Jane}} {x/OJ, y/John}} {y/John, x/Mother(John)}} {fail} • Standardizing apart eliminates overlap of variables, e. g. , Knows(z 17, OJ)

Unification • We can get the inference immediately if we can find a substitution θ such that King(x) and Greedy(x) match King(John) and Greedy(y) θ = {x/John, y/John} works • Unify(α, β) = θ if αθ = βθ p Knows(John, x) q Knows(John, Jane) Knows(y, OJ) Knows(y, Mother(y)) Knows(x, OJ) θ {x/Jane}} {x/OJ, y/John}} {y/John, x/Mother(John)}} {fail} • Standardizing apart eliminates overlap of variables, e. g. , Knows(z 17, OJ)

Unification • To unify Knows(John, x) and Knows(y, z), θ = {y/John, x/z } or θ = {y/John, x/John, z/John} • The first unifier is more general than the second. • There is a single most general unifier (MGU) that is unique up to renaming of variables. MGU = { y/John, x/z }

The unification algorithm

The unification algorithm

Example knowledge base • The law says that it is a crime for an American to sell weapons to hostile nations. The country Nono, an enemy of America, has some missiles, and all of its missiles were sold to it by Colonel West, who is American. • Prove that Col. West is a criminal

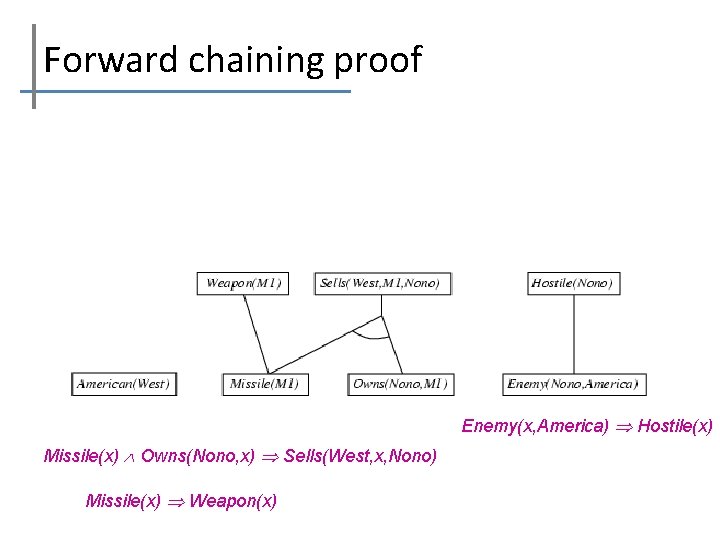
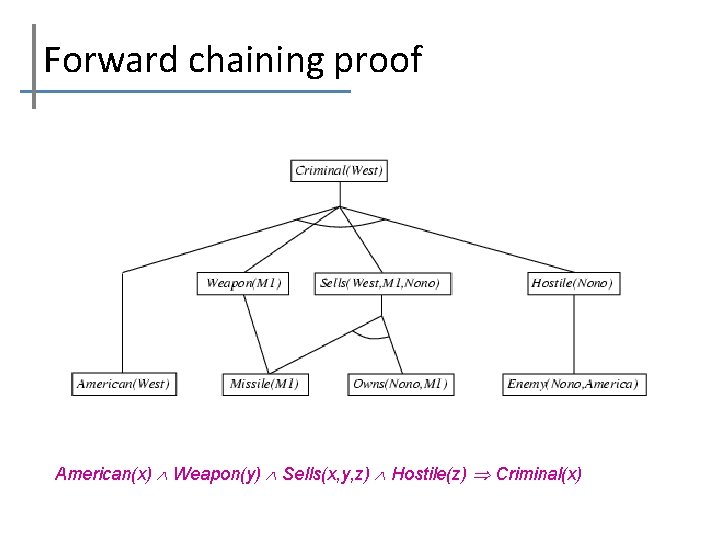
Example knowledge base contd. . it is a crime for an American to sell weapons to hostile nations: American(x) Weapon(y) Sells(x, y, z) Hostile(z) Criminal(x) Nono … has some missiles, i. e. , x Owns(Nono, x) Missile(x): Owns(Nono, M 1) and Missile(M 1) … all of its missiles were sold to it by Colonel West Missile(x) Owns(Nono, x) Sells(West, x, Nono) Missiles are weapons: Missile(x) Weapon(x) An enemy of America counts as "hostile“: Enemy(x, America) Hostile(x) West, who is American … American(West) The country Nono, an enemy of America … Enemy(Nono, America)

Forward chaining algorithm

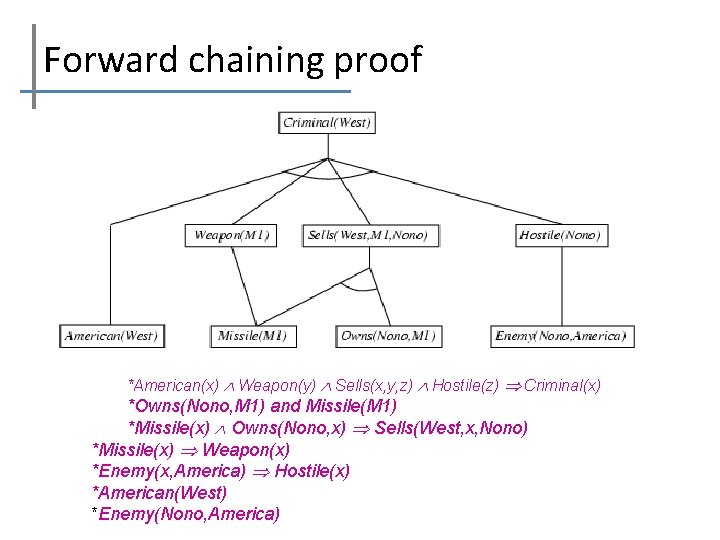
Forward chaining proof

Forward chaining proof Enemy(x, America) Hostile(x) Missile(x) Owns(Nono, x) Sells(West, x, Nono) Missile(x) Weapon(x)

Forward chaining proof American(x) Weapon(y) Sells(x, y, z) Hostile(z) Criminal(x)

Forward chaining proof *American(x) Weapon(y) Sells(x, y, z) Hostile(z) Criminal(x) *Owns(Nono, M 1) and Missile(M 1) *Missile(x) Owns(Nono, x) Sells(West, x, Nono) *Missile(x) Weapon(x) *Enemy(x, America) Hostile(x) *American(West) *Enemy(Nono, America)

Properties of forward chaining • Sound and complete for first-order definite clauses • Datalog = first-order definite clauses + no functions • FC terminates for Datalog in finite number of iterations • May not terminate in general if α is not entailed • This is unavoidable: entailment with definite clauses is semidecidable

Efficiency of forward chaining Incremental forward chaining: no need to match a rule on iteration k if a premise wasn't added on iteration k-1 match each rule whose premise contains a newly added positive literal Matching itself can be expensive: Database indexing allows O(1) retrieval of known facts – e. g. , query Missile(x) retrieves Missile(M 1) Forward chaining is widely used in deductive databases

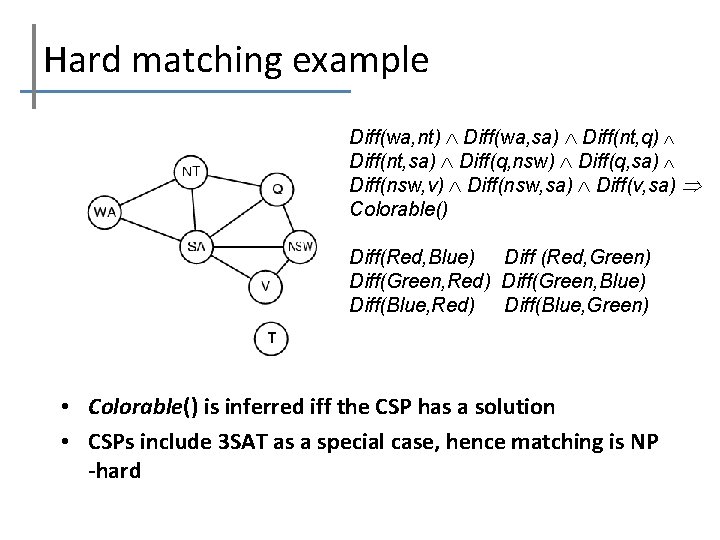
Hard matching example Diff(wa, nt) Diff(wa, sa) Diff(nt, q) Diff(nt, sa) Diff(q, nsw) Diff(q, sa) Diff(nsw, v) Diff(nsw, sa) Diff(v, sa) Colorable() Diff(Red, Blue) Diff (Red, Green) Diff(Green, Red) Diff(Green, Blue) Diff(Blue, Red) Diff(Blue, Green) • Colorable() is inferred iff the CSP has a solution • CSPs include 3 SAT as a special case, hence matching is NP -hard

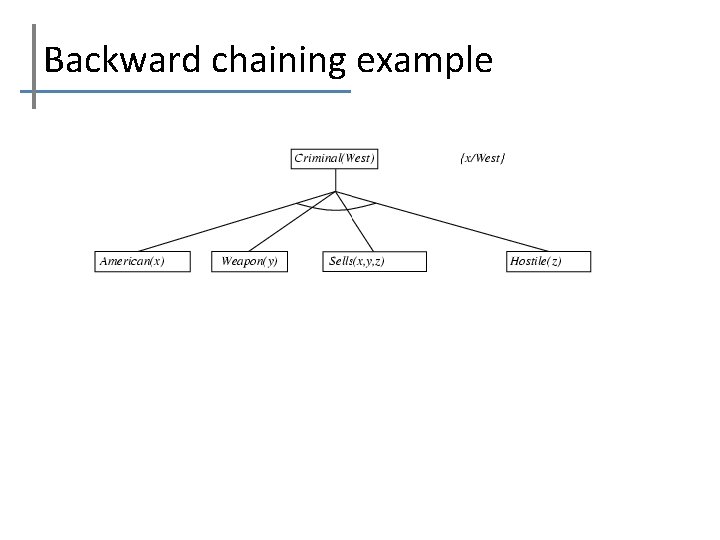
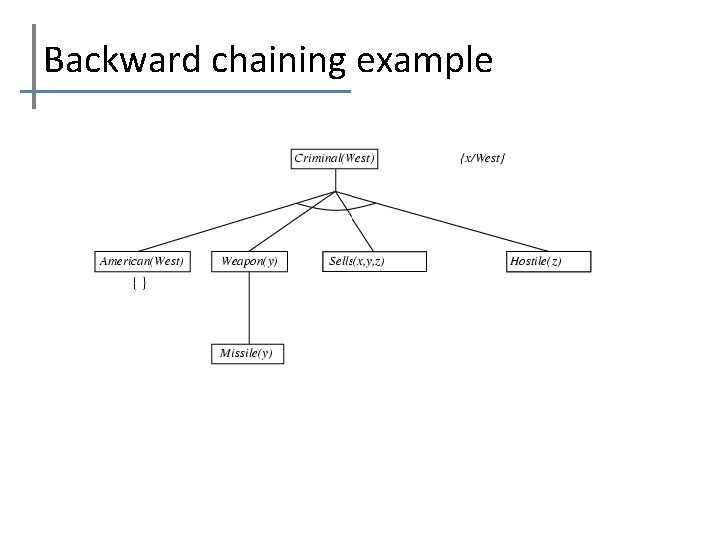
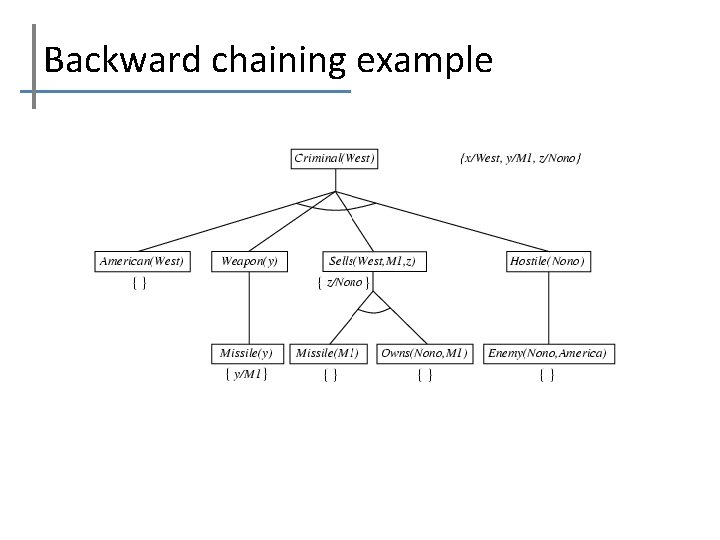
Backward chaining example

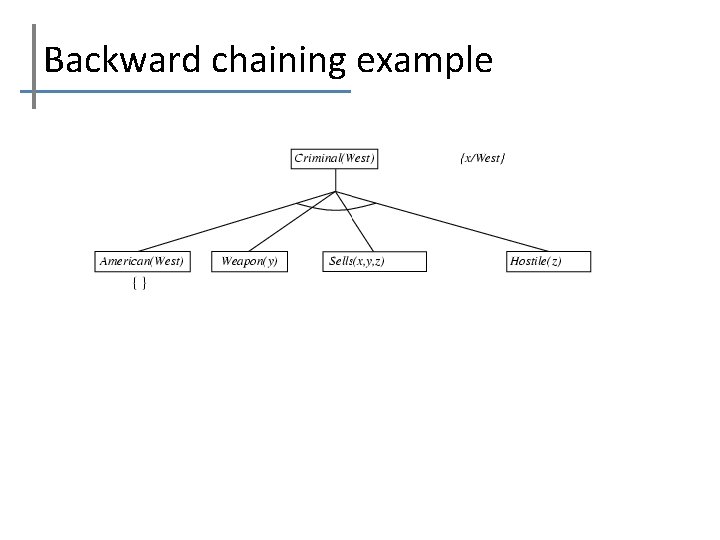
Backward chaining example

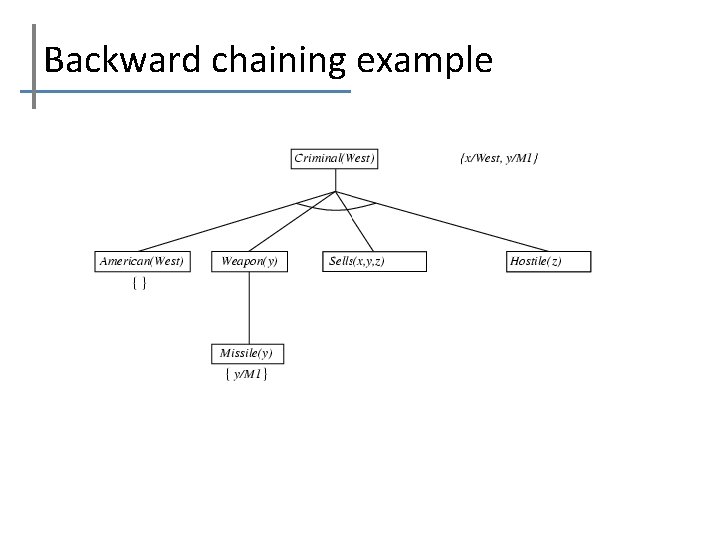
Backward chaining example

Backward chaining example

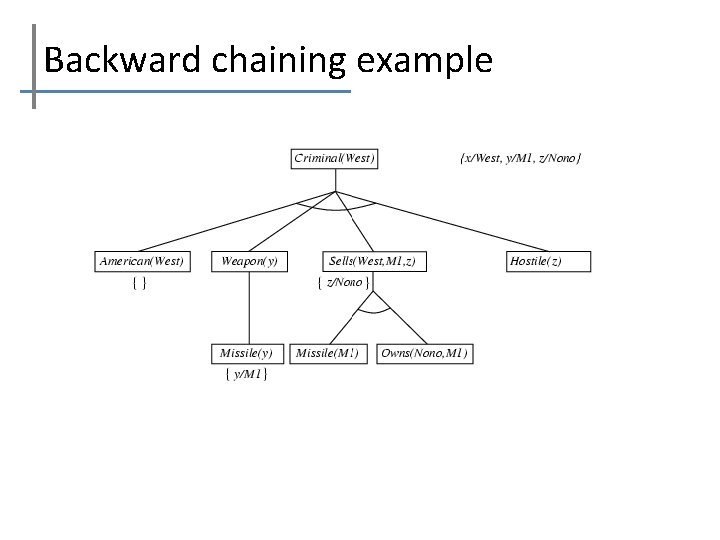
Backward chaining example

Backward chaining example

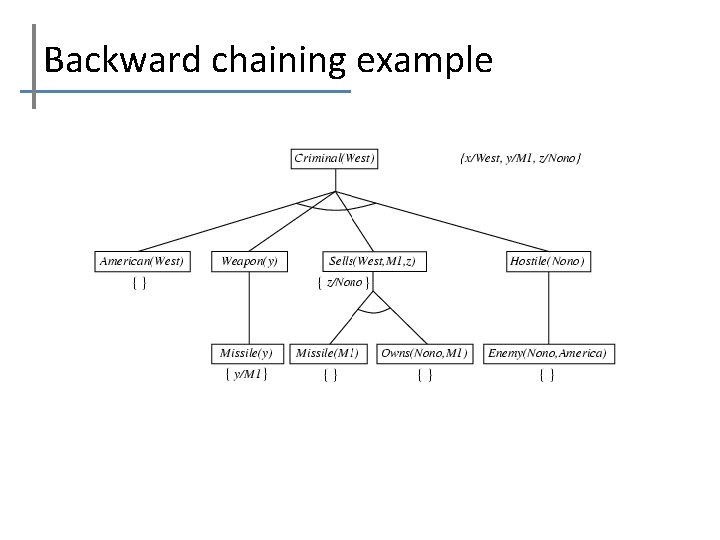
Backward chaining example

Backward chaining example

Backward chaining algorithm SUBST(COMPOSE(θ 1, θ 2), p) = SUBST(θ 2, SUBST(θ 1, p))

Properties of backward chaining • Depth-first recursive proof search: space is linear in size of proof • Incomplete due to infinite loops fix by checking current goal against every goal on stack • Inefficient due to repeated subgoals (both success and failure) fix using caching of previous results (extra space) • Widely used for logic programming

Logic programming: Prolog • Algorithm = Logic + Control • Basis: backward chaining with Horn clauses + bells & whistles Widely used in Europe, Japan (basis of 5 th Generation project) Compilation techniques 60 million LIPS • Program = set of clauses = head : - literal 1, … literaln. criminal(X) : - american(X), weapon(Y), sells(X, Y, Z), hostile(Z). • • • Depth-first, left-to-right backward chaining Built-in predicates for arithmetic etc. , e. g. , X is Y*Z+3 Built-in predicates that have side effects (e. g. , input and output • • predicates, assert/retract predicates) Closed-world assumption ("negation as failure") – e. g. , given alive(X) : - not dead(X). – alive(joe) succeeds if dead(joe) fails
![Prolog Appending two lists to produce a third append Y Y appendXL Y Prolog • Appending two lists to produce a third: append([], Y, Y). append([X|L], Y,](https://slidetodoc.com/presentation_image/e0a4842605f17b7f5ecc25a7a3f7bd14/image-80.jpg)
Prolog • Appending two lists to produce a third: append([], Y, Y). append([X|L], Y, [X|Z]) : - append(L, Y, Z). • query: append(A, B, [1, 2]) ? • answers: A=[] B=[1, 2] A=[1] B=[2] A=[1, 2] B=[]

Resolution: brief summary • Full first-order version: l 1 ··· lk, m 1 ··· mn (l 1 ··· li-1 li+1 ··· lk m 1 ··· mj-1 mj+1 ··· mn)θ where Unify(li, mj) = θ. • The two clauses are assumed to be standardized apart so that they share no variables. • For example, Rich(x) Unhappy(x) Rich(Ken) Unhappy(Ken) with θ = {x/Ken} • Apply resolution steps to CNF(KB α); complete for FOL

Conversion to CNF • Everyone who loves all animals is loved by someone: x [ y Animal(y) Loves(x, y)] [ y Loves(y, x)] 1. Eliminate biconditionals and implications x [ y Animal(y) Loves(x, y)] [ y Loves(y, x)] 2. Move inwards: x p ≡ x p, x p ≡ x p x [ y ( Animal(y) Loves(x, y))] [ y Loves(y, x)] x [ y Animal(y) Loves(x, y)] [ y Loves(y, x)] x [ y Animal(y) Loves(x, y)] [ y Loves(y, x)]

Conversion to CNF contd. 3. Standardize variables: each quantifier should use a different one x [ y Animal(y) Loves(x, y)] [ z Loves(z, x)] • • • Skolemize: a more general form of existential instantiation. Each existential variable is replaced by a Skolem function of the enclosing universally quantified variables: x [Animal(F(x)) Loves(x, F(x))] Loves(G(x), x) Drop universal quantifiers: [Animal(F(x)) Loves(x, F(x))] Loves(G(x), x) Distribute over : [Animal(F(x)) Loves(G(x), x)] [ Loves(x, F(x)) Loves(G(x), x)]

Example knowledge base contd. . it is a crime for an American to sell weapons to hostile nations: American(x) Weapon(y) Sells(x, y, z) Hostile(z) Criminal(x) Nono … has some missiles, i. e. , x Owns(Nono, x) Missile(x): Owns(Nono, M 1) and Missile(M 1) … all of its missiles were sold to it by Colonel West Missile(x) Owns(Nono, x) Sells(West, x, Nono) Missiles are weapons: Missile(x) Weapon(x) An enemy of America counts as "hostile“: Enemy(x, America) Hostile(x) West, who is American … American(West) The country Nono, an enemy of America … Enemy(Nono, America)

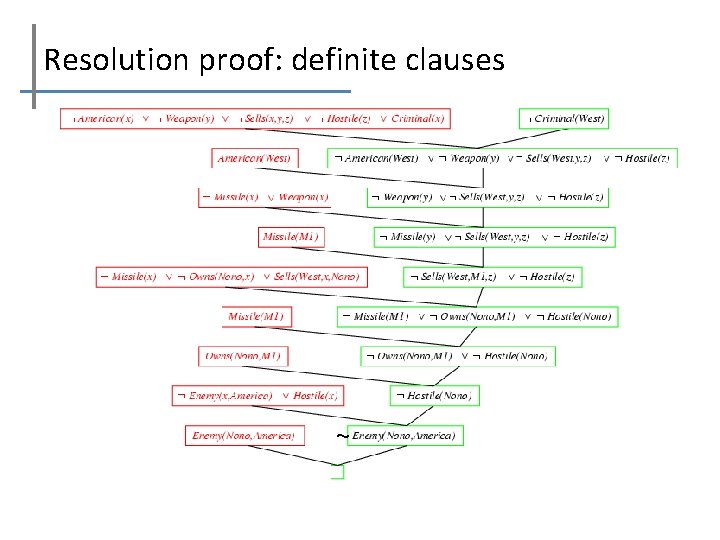
Resolution proof: definite clauses ~

Converting to clause form Prove I(A, 27)

Example: Resolution Refutation Prove I(A, 27)

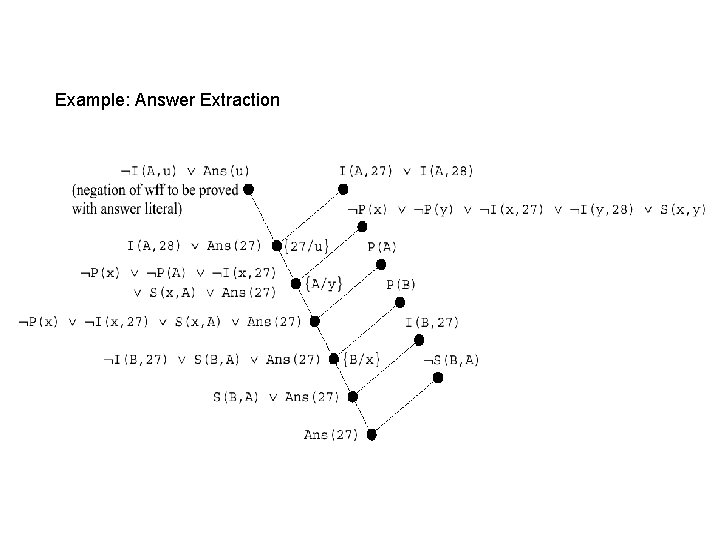
Example: Answer Extraction
 First order logic vs propositional logic
First order logic vs propositional logic First order logic vs propositional logic
First order logic vs propositional logic First order logic vs propositional logic
First order logic vs propositional logic Fol in ai
Fol in ai Inference in first order logic in artificial intelligence
Inference in first order logic in artificial intelligence First order logic syntax
First order logic syntax Slot filler
Slot filler First order logic unification
First order logic unification The first order chapter 8
The first order chapter 8 Generalized modus ponens
Generalized modus ponens The first order chapter 8
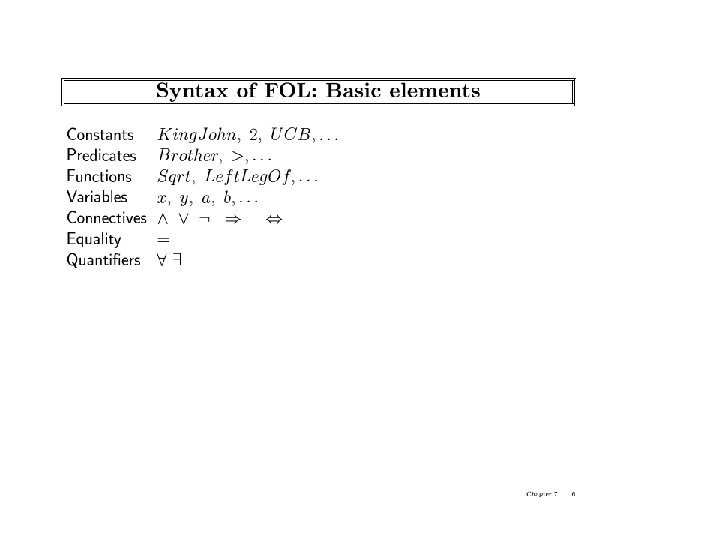
The first order chapter 8 Syntax of first order logic
Syntax of first order logic Uniqueness quantifier equivalence
Uniqueness quantifier equivalence Via optica
Via optica Pg 171
Pg 171 Lei 171 de 2007
Lei 171 de 2007 Nosotros salir
Nosotros salir Nonlinear pricing example
Nonlinear pricing example Ai 171
Ai 171 Ai 171
Ai 171 Tax allowance meaning
Tax allowance meaning 171 nomreli mekteb
171 nomreli mekteb 171 nomreli mekteb
171 nomreli mekteb Decret 171/2015
Decret 171/2015 Dot
Dot Cs 171 uci
Cs 171 uci 171 in binary
171 in binary 171 nomreli mekteb
171 nomreli mekteb 171 sayli mekteb
171 sayli mekteb First order change examples
First order change examples First order cybernetics and second order cybernetics
First order cybernetics and second order cybernetics Free fall 2016
Free fall 2016 Concurrent vs sequential
Concurrent vs sequential Cryptarithmetic problem logic+logic=prolog
Cryptarithmetic problem logic+logic=prolog Software development plan
Software development plan Majority circuit
Majority circuit Combinational logic sequential logic 차이
Combinational logic sequential logic 차이 Combinational logic sequential logic
Combinational logic sequential logic Where does the logic of this advertisement fall short
Where does the logic of this advertisement fall short With high honors
With high honors Deped order no 39 s 2016
Deped order no 39 s 2016 Third order logic
Third order logic Third order logic
Third order logic Third order logic
Third order logic Logic
Logic Fixed logic devices examples
Fixed logic devices examples Logic functions
Logic functions The fpga is a fixed-function device
The fpga is a fixed-function device Natural order of a sentence
Natural order of a sentence Order taker vs order getter
Order taker vs order getter Difference between 1st order and zero order kinetics
Difference between 1st order and zero order kinetics Zero order elimination drugs
Zero order elimination drugs Law is order and good law is good order
Law is order and good law is good order Order/properties-order
Order/properties-order In order issue in order completion example
In order issue in order completion example In order issue in order completion example
In order issue in order completion example Arbol in order post order
Arbol in order post order First second and third order neurons
First second and third order neurons Rate of elimination of drug
Rate of elimination of drug Taylors theorem
Taylors theorem Rate of reaction
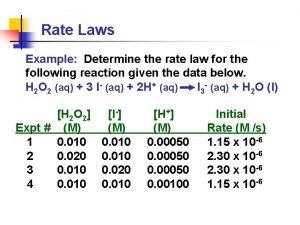
Rate of reaction How to determine the rate law of a reaction
How to determine the rate law of a reaction Determine
Determine First order rate law
First order rate law First order elimination
First order elimination Order of increasing first ionization energy
Order of increasing first ionization energy Ordinary differential equations definition
Ordinary differential equations definition Bode plot of integrator
Bode plot of integrator 1st order derivative formula
1st order derivative formula First-order differential equations
First-order differential equations First order stochastically dominates
First order stochastically dominates Laws jespersen
Laws jespersen Differentiation gradient
Differentiation gradient Competitive inhibition
Competitive inhibition First order phase transition
First order phase transition Sinusoidal response of first order system
Sinusoidal response of first order system First order pde
First order pde Solving 1st order differential equations
Solving 1st order differential equations Integrating factor of differential equation
Integrating factor of differential equation Rc first order circuit
Rc first order circuit First order stochastically dominates
First order stochastically dominates Integrating factor formula
Integrating factor formula Pde
Pde First second and third order neurons
First second and third order neurons Half life equation for first order
Half life equation for first order Analytical solution of first order differential equation
Analytical solution of first order differential equation Order of increasing first ionization energy
Order of increasing first ionization energy Control systems overshoot
Control systems overshoot First order stochastically dominates
First order stochastically dominates