Lecture 4 on Individual Optimization Risk Aversion Last



















- Slides: 22

Lecture 4 on Individual Optimization Risk Aversion Last lecture we investigated the independence axiom and the expected utility hypothesis. A more direct approach is to design experiments that reveal a person’s attitudes towards risk and uncertainty, the topic of today’s lecture.

Certainty Equivalence Instead of pursuing an axiomatic approach to modeling human behavior under uncertainty, we could more directly determine their attitude towards risk. An important concept is how much a person is willing to pay to avoid a risk, or equivalently, how much they are willing to pay to gamble. (Parenthetically we note that gambling is one of the biggest recreational activities in the U. S. )

Measuring certainty equivalence How much a person is willing to pay for a lottery depends both on the person and also on the lottery. Experimental methods have been used to determine a person’s certainty equivalent to well specified lotteries. In this class we shall consider lotteries which have up to 11 outcomes. They offer the chance to pay $100 with probability p 10, $90 with probability p 9, . . . , and $0 with probability p 0.

An experiment In this experiment you are asked to how much you are willing to pay for a lottery called L when you know its probabilities. Call that number b for bid. We then draw a random number n from a probability distribution which lies between (that has support on) 0 and 100. If n b, then you pay n in exchange for the lottery L, and receive the payoff from playing the lottery. If b < n, then you neither pay nor receive anything.

The lotteries Each of these lotteries can be defined by 10 numbers (lying the 10 dimensional simplex), where the first element is p 10, the second is p 9, and so on. We only have to write down 10 elements even though there are 11 outcomes because: p 0 = 1 - p 10 - p 9 -. . . - p 1. The lotteries you will bid on are listed below: (0. 5, 0, 0, . . . , 0) (0. 0909’, . . , 0. 0909’) (0. 1, . . , 0. 1)

Verbal explanation The first lottery pays $100 half the time and $0 half the time. The second lottery pays $100 one eleventh of the time, $90 one eleventh of the time, . . . , and $0 eleventh tenth of the time. The third lottery pays $100 one tenth of the time, $90 one tenth of the time, . . . , and $10 one tenth of the time, so always pays out something.

Bidding below your certainty equivalent Suppose your certainty equivalent lottery for L is the value v. How should you choose b? If you bid b < v you gain v – n whenever n b, and zero otherwise. This bidding strategy guarantees that you never lose. However if b < n < v, you miss the gain from buying the lottery at a price less than your valuation. If you had bid between n and v instead, you would have gained v – n.

Bidding above your certainty equivalent If you bid b > v, you gain v – n whenever n v and you lose n – v if v < n b. Otherwise b < n and you neither gain nor lose. The potential for loss from this strategy can be mitigated by reducing your bid. If you bid some number b 1 between v and b, then you still gain v – n whenever n v and you don’t lose anything if v b 1 < n b.

Optimal bidding strategy The two previous slides have probably convinced you that the optimal choice is to bid b = v. In this case you gain v – n whenever n v and zero otherwise. Therefore experimental subjects who know how to make an optimal bid will truthfully reveal their certainty equivalent v for the lottery L.

Expected utility and certainty equivalence Suppose the outcomes called x are ordered by your own preferences from the worst to the best, and let u(x) denote the utility from the random variable x. (For example money outcomes are always ordered that way, since more is preferred to less!) Assume your preferences obey the expected utility hypothesis. Then your expected utility from playing a lottery F is EF[u(x)], where E denotes the expectations operator. It follows that your certainty equivalent for F is the value v. F which solves u(v. F) = EF[u(x)]

Expected utility and attitudes towards risk In this case we can characterize you attitude towards risk quite simply. If you are risk neutral, then v. F = EF[x] for all F, and hence we can write u(x) = x. If you are a risk lover, meaning v. F > EF[x] for all F, then u(x) is convex. If you are a risk avoider, meaning v. F < EF[x] for all F, then u(x) is concave.

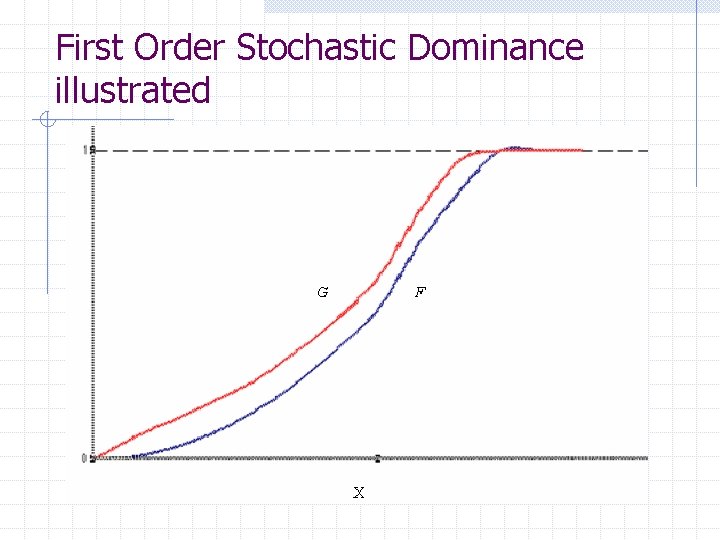
First-order stochastic dominance Consider two different probability distributions F(x) and G(x). That is F(x) G(x) for some real number x. We say that F first-order stochastically dominates G if and only F(x) G(x) for all x. This is formally equivalent to saying that if x is a random variable drawn from G(x), if y is a random variable that only takes on positive values, and F(z) is the probability distribution function for z = x + y, then F first-order stochastically dominates G.

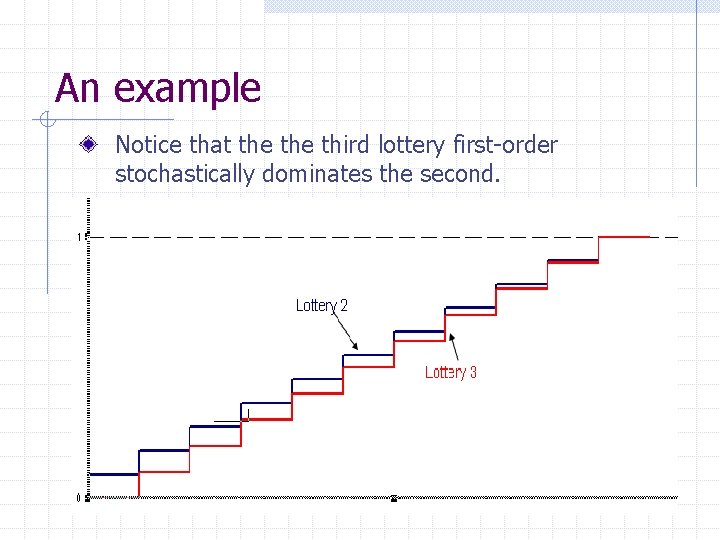
An example Notice that the third lottery first-order stochastically dominates the second.

First Order Stochastic Dominance illustrated

First-order stochastic dominance and expected utility Now consider those people who obey the expected utility hypothesis, and order the outcomes x, a random variable from the lowest (least preferred) to the highest (most preferred). They obtain expected utility EF[u(x)] from playing lottery F, but the function u(x) differs from person to person. Can we rank EF[u(x)] and EG[u(x)] when F first order stochastically dominates G?

Theorem If F first-order stochastically dominates G, then every expected utility maximizer with u(x) increasing in x, prefers F to G.

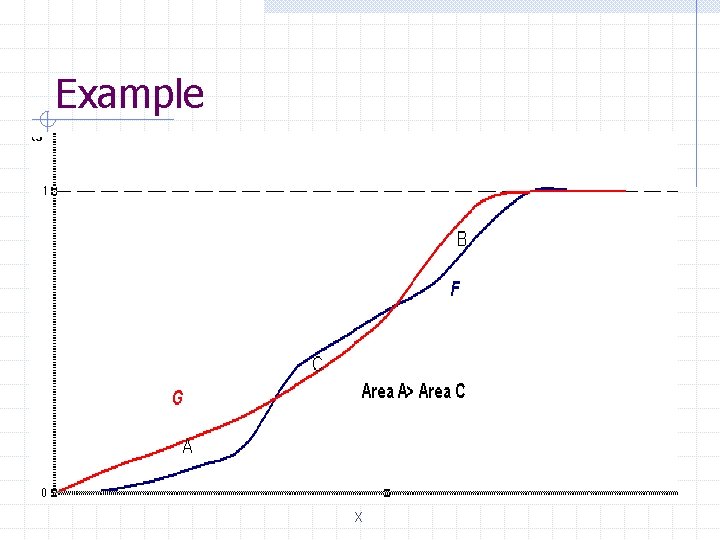
Second-order stochastic dominance Consider two different probability distributions F(x) and G(y) with the same mean. That is EF[x]= EG[x]. We say that F second-order stochastically dominates G if and only for all t: This is saying that if x is a random variable drawn from G(x), if y is a random variable with mean 0, and that probability distribution function for z = x + y is F(z) , then F second-order stochastically dominates G.

Example X

Second-order stochastic dominance and expected utility Assume a person follows the expected utility hypothesis, and thus obtains expected utility EF[u(x)] from playing a lottery F. We now assume u(x) is concave increasing in x, implying that the person is risk averse, but we impose no other restrictions on u(x). Suppose EF[x]= EG[x]. Then a risk averse person prefers F to G, that is v. G v. F if and only if F second -order stochastically dominates G.

Another theorem Suppose F and G have the same mean. Then a risk averse person prefers F to G if and only if F secondorder stochastically dominates G.

Investing in a risky asset We now modify the lottery experiment. Instead of bidding on a lottery, you are asked to choose how many units of each independently distributed lottery you would like to buy A unit of each lottery costs $50, and you can spend up to $50, 000. Your total payoff are your lottery winnings plus unspent cash. The payoff from the lotteries you are listed below: - Firm A : [$10 with probability 0. 5 and $100 with probability 0. 5] - Firm B : [$10 with probability 0. 1, $20 with probability 0. 10, . . . , $100 with probability 0. 1] - Firm C : [$20 with probability 0. 2, $30 with 0. 1, $40 with probability 0. 1, . . . , $100 with probability 0. 1]

Optimal Insurance A risk averse person fully insures himself against a calamity if actuarially fair insurance is available. This follows from the fact that for risk averters the certainty equivalent of a gamble is greater than its expected value. By the same argument we have used on portfolio choices, a risk averter will not fully insure himself if the rates are not actuarially fair. He will retain ownership over a portion of the lottery.