CS 171 Discussion Session Week 3 Jia Chen







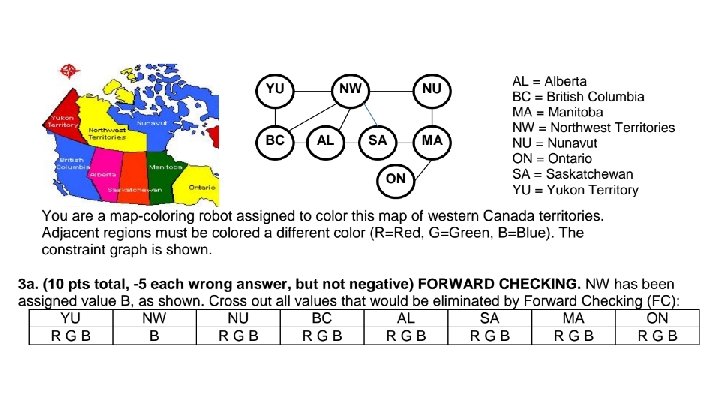
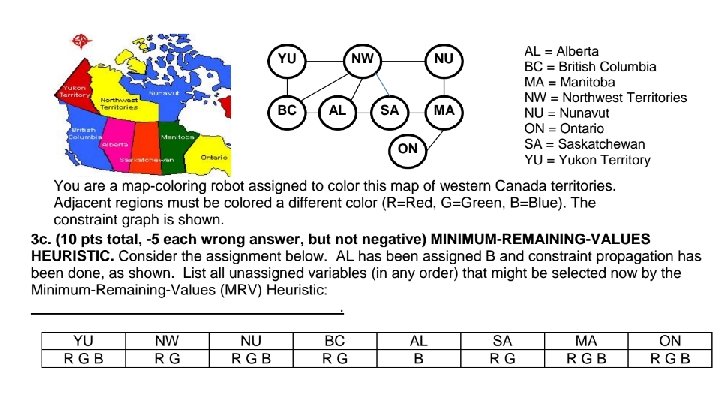
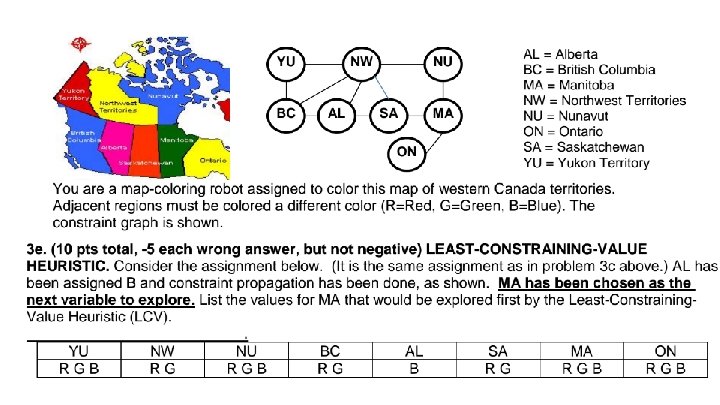
- Slides: 34

CS 171 Discussion Session Week 3 Jia Chen jiac 5@uci. edu

Quiz 1 return First letter of your last name A - H: Kyoungwon Kim (Office hours Tuesday 9 -10 am in ICS 424 A) I - P: Zephyr Yao (Office hours Monday 9 -10 am in ICS 424 F) Q - Z: Dongxu Zhao (Office hours Friday 9 -10 am in ICS 424 F) If time conflicts, send email to the Reader to which you are assigned, and to a Reader with whom you do not have a time conflict, asking to be reassigned.

Schedule Games (Minimax, Alpha-beta pruning) CSP

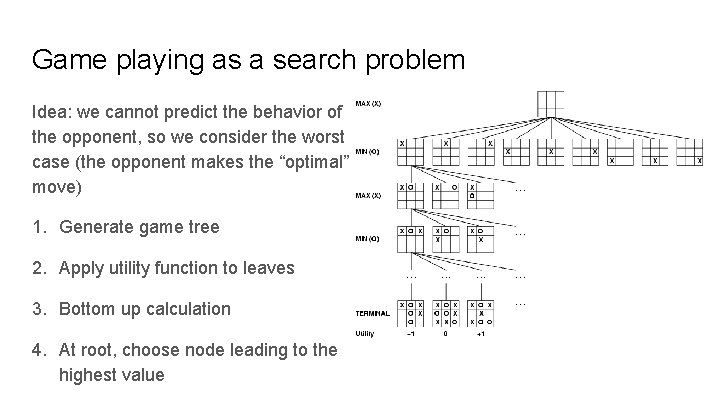
Game playing as a search problem Idea: we cannot predict the behavior of the opponent, so we consider the worst case (the opponent makes the “optimal” move) 1. Generate game tree 2. Apply utility function to leaves 3. Bottom up calculation 4. At root, choose node leading to the highest value

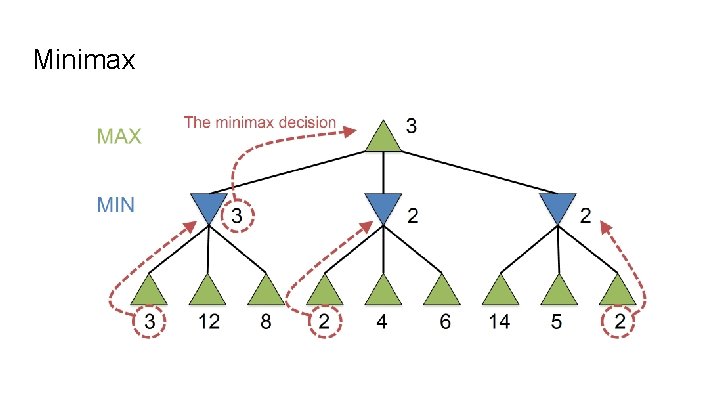
Minimax

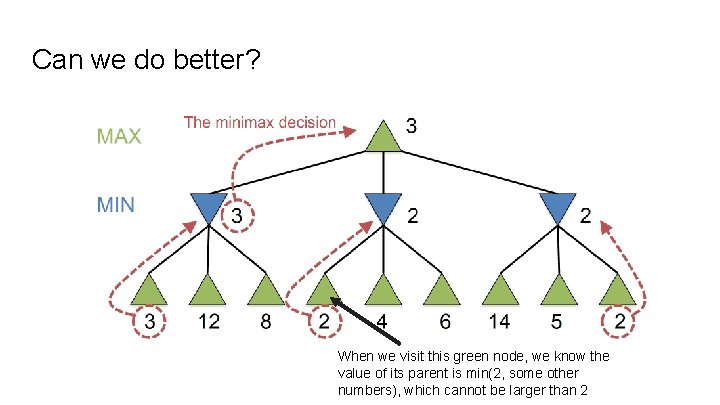
Can we do better? When we visit this green node, we know the value of its parent is min(2, some other numbers), which cannot be larger than 2

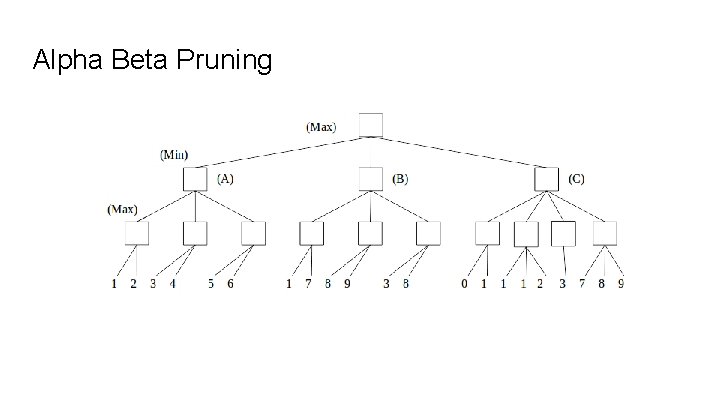
Alpha Beta Pruning

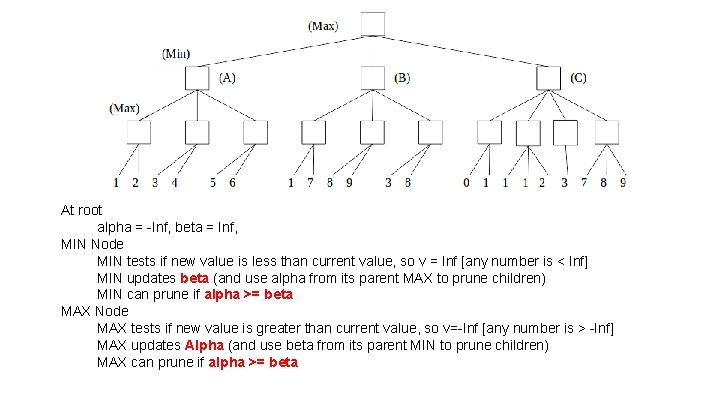
At root alpha = -Inf, beta = Inf, MIN Node MIN tests if new value is less than current value, so v = Inf [any number is < Inf] MIN updates beta (and use alpha from its parent MAX to prune children) MIN can prune if alpha >= beta MAX Node MAX tests if new value is greater than current value, so v=-Inf [any number is > -Inf] MAX updates Alpha (and use beta from its parent MIN to prune children) MAX can prune if alpha >= beta

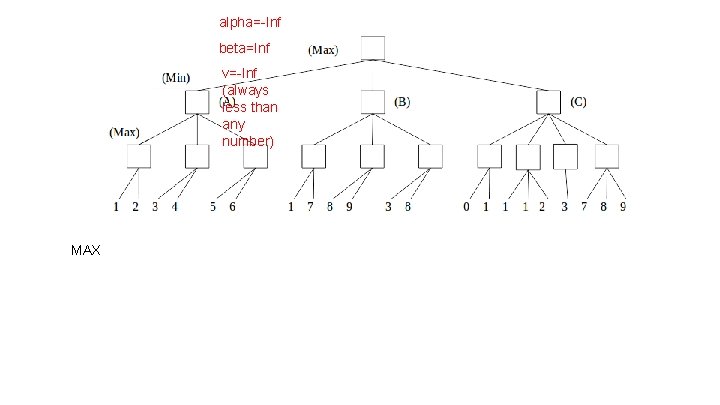
alpha=-Inf beta=Inf v=-Inf (always less than any number) MAX

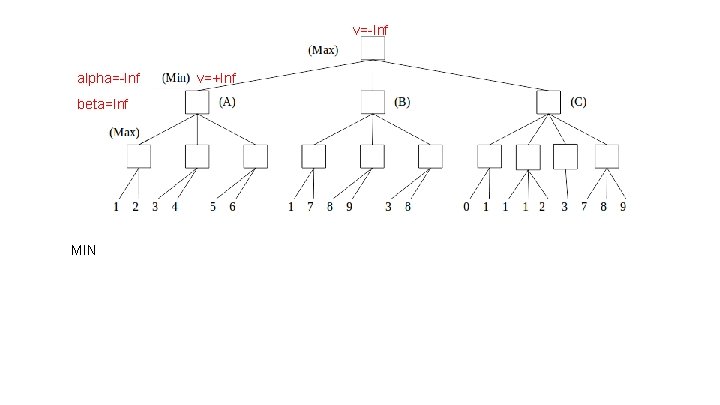
v=-Inf alpha=-Inf beta=Inf MIN v=+Inf

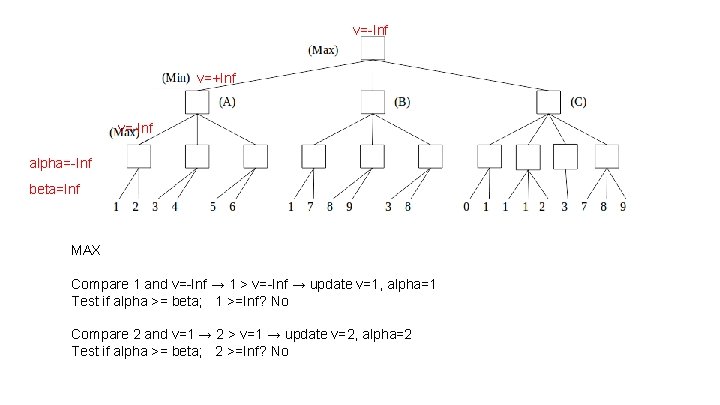
v=-Inf v=+Inf v=-Inf alpha=-Inf beta=Inf MAX Compare 1 and v=-Inf → 1 > v=-Inf → update v=1, alpha=1 Test if alpha >= beta; 1 >=Inf? No Compare 2 and v=1 → 2 > v=1 → update v=2, alpha=2 Test if alpha >= beta; 2 >=Inf? No

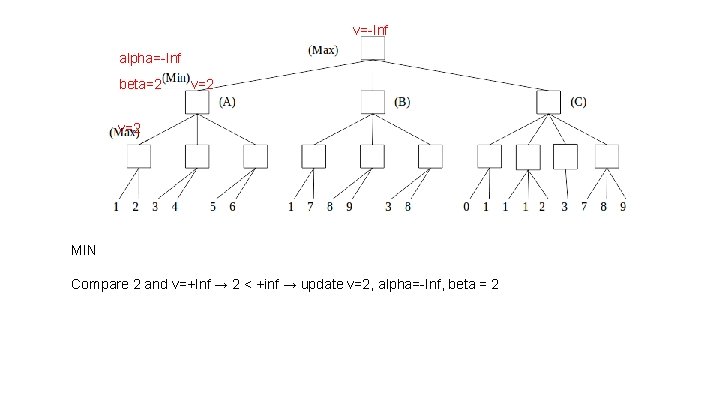
v=-Inf alpha=-Inf beta=2 v=2 MIN Compare 2 and v=+Inf → 2 < +inf → update v=2, alpha=-Inf, beta = 2

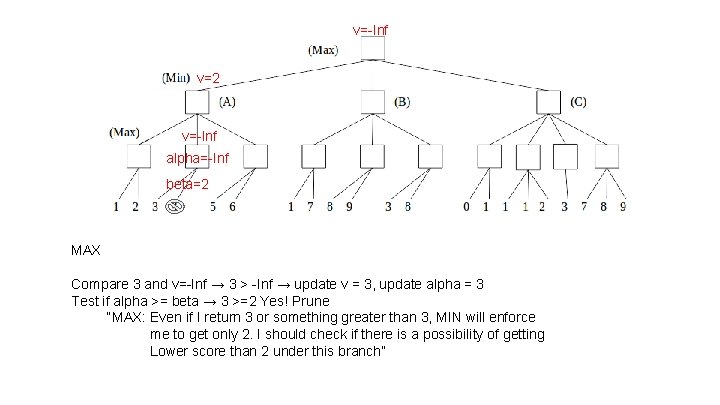
v=-Inf v=2 v=-Inf alpha=-Inf beta=2 MAX Compare 3 and v=-Inf → 3 > -Inf → update v = 3, update alpha = 3 Test if alpha >= beta → 3 >=2 Yes! Prune “MAX: Even if I return 3 or something greater than 3, MIN will enforce me to get only 2. I should check if there is a possibility of getting Lower score than 2 under this branch”

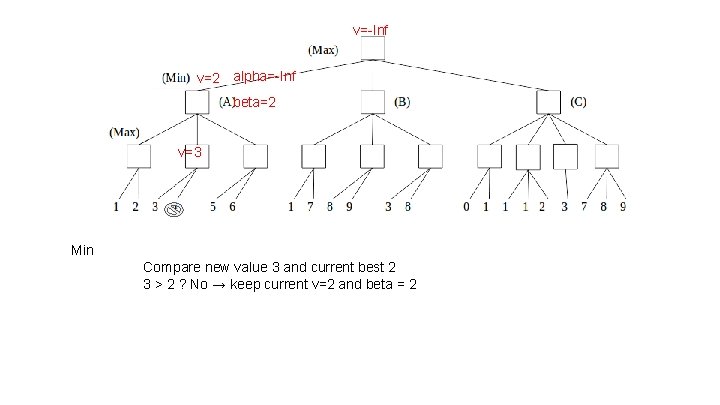
v=-Inf v=2 alpha=-Inf beta=2 v=3 Min Compare new value 3 and current best 2 3 > 2 ? No → keep current v=2 and beta = 2

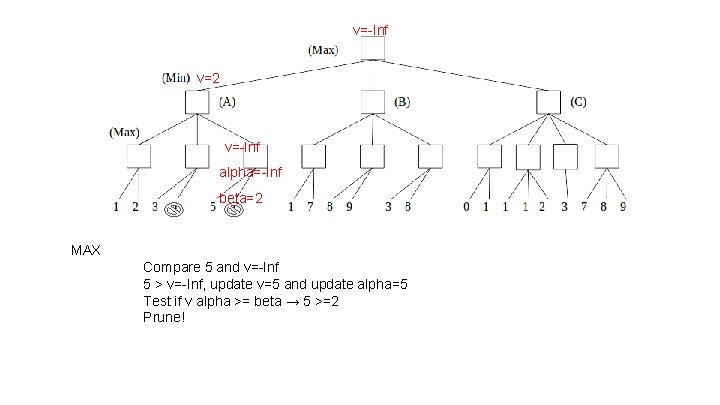
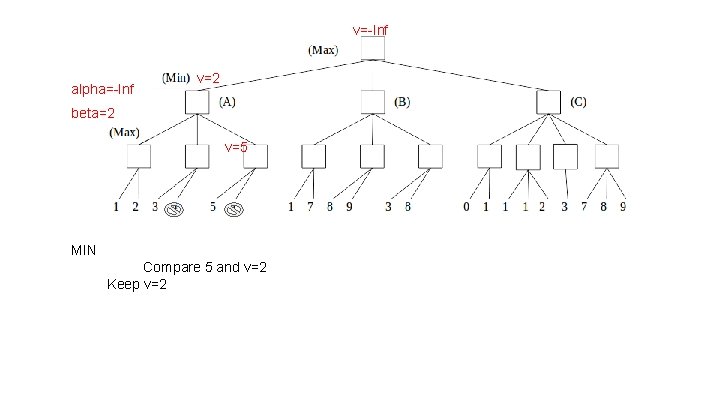
v=-Inf v=2 v=-Inf alpha=-Inf beta=2 MAX Compare 5 and v=-Inf 5 > v=-Inf, update v=5 and update alpha=5 Test if v alpha >= beta → 5 >=2 Prune!

v=-Inf alpha=-Inf v=2 beta=2 v=5 MIN Compare 5 and v=2 Keep v=2

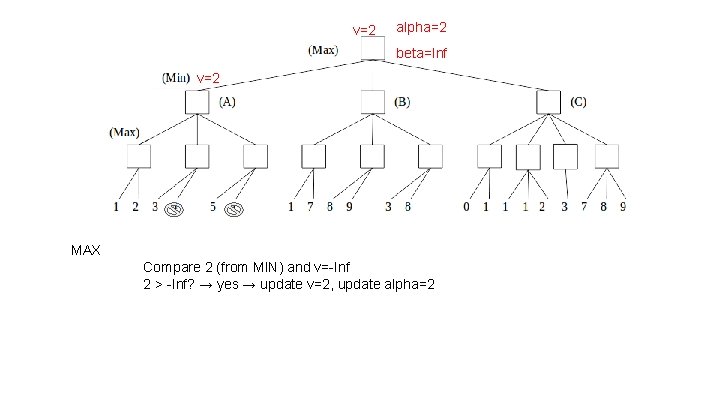
v=2 alpha=2 beta=Inf v=2 MAX Compare 2 (from MIN) and v=-Inf 2 > -Inf? → yes → update v=2, update alpha=2

v=2 alpha=2 beta=Inf MIN v=Inf

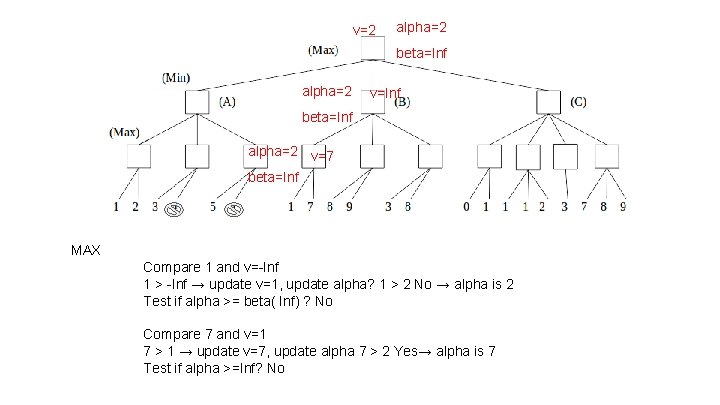
v=2 alpha=2 beta=Inf alpha=2 v=Inf beta=Inf alpha=2 v=7 beta=Inf MAX Compare 1 and v=-Inf 1 > -Inf → update v=1, update alpha? 1 > 2 No → alpha is 2 Test if alpha >= beta( Inf) ? No Compare 7 and v=1 7 > 1 → update v=7, update alpha 7 > 2 Yes→ alpha is 7 Test if alpha >=Inf? No

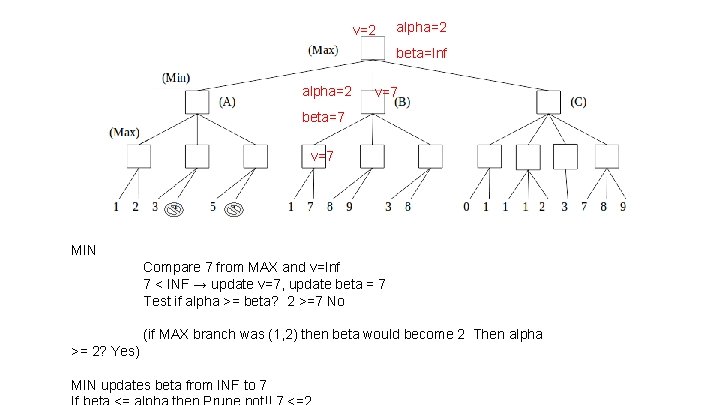
v=2 alpha=2 beta=Inf alpha=2 v=7 beta=7 v=7 MIN Compare 7 from MAX and v=Inf 7 < INF → update v=7, update beta = 7 Test if alpha >= beta? 2 >=7 No (if MAX branch was (1, 2) then beta would become 2 Then alpha >= 2? Yes) MIN updates beta from INF to 7

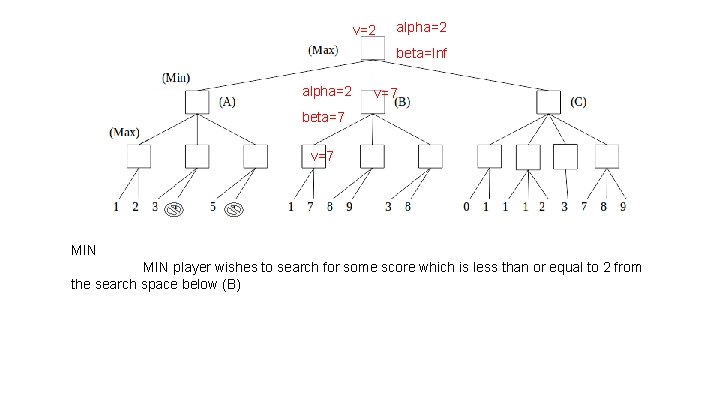
v=2 alpha=2 beta=Inf alpha=2 v=7 beta=7 v=7 MIN player wishes to search for some score which is less than or equal to 2 from the search space below (B)

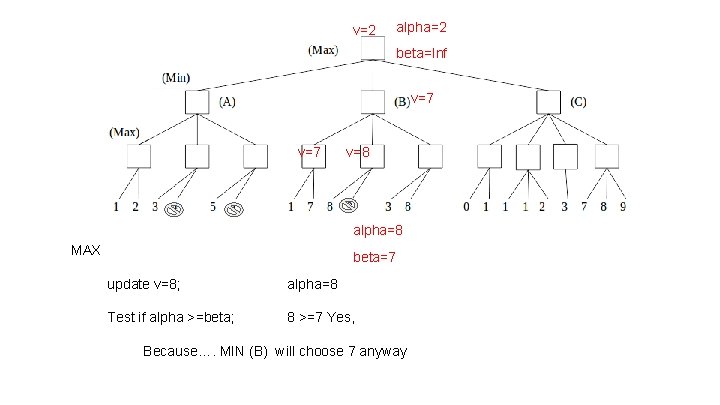
v=2 alpha=2 beta=Inf v=7 v=8 alpha=8 MAX beta=7 update v=8; alpha=8 Test if alpha >=beta; 8 >=7 Yes, Because…. MIN (B) will choose 7 anyway

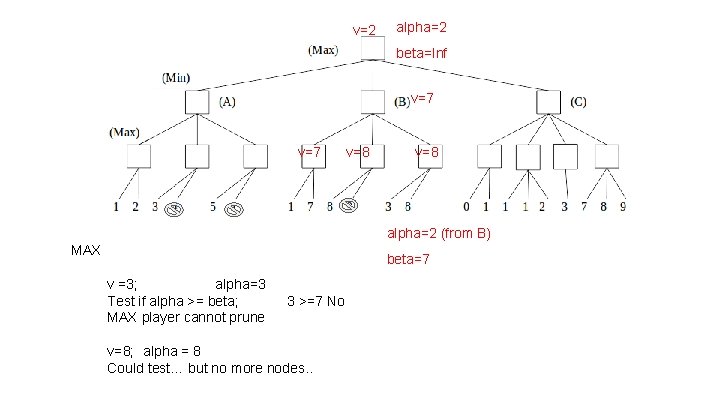
v=2 alpha=2 beta=Inf v=7 v=8 alpha=2 (from B) MAX beta=7 v =3; alpha=3 Test if alpha >= beta; MAX player cannot prune 3 >=7 No v=8; alpha = 8 Could test… but no more nodes. .

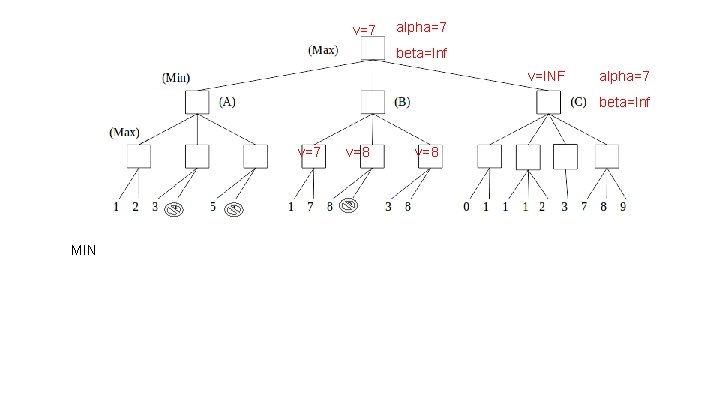
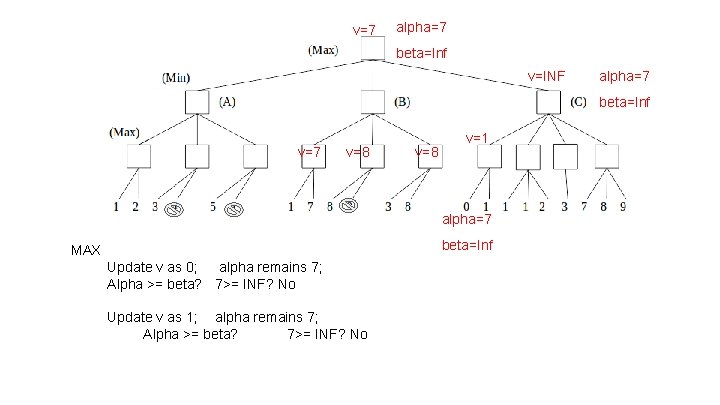
v=7 alpha=7 beta=Inf v=INF alpha=7 beta=Inf v=7 MIN v=8

v=7 alpha=7 beta=Inf v=INF alpha=7 beta=Inf v=7 v=8 v=1 alpha=7 beta=Inf MAX Update v as 0; alpha remains 7; Alpha >= beta? 7>= INF? No Update v as 1; alpha remains 7; Alpha >= beta? 7>= INF? No

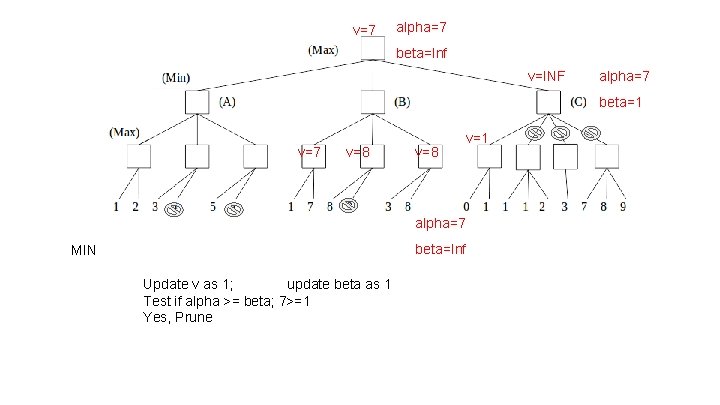
v=7 alpha=7 beta=Inf v=INF alpha=7 beta=1 v=7 v=8 v=1 alpha=7 beta=Inf MIN Update v as 1; update beta as 1 Test if alpha >= beta; 7>=1 Yes, Prune

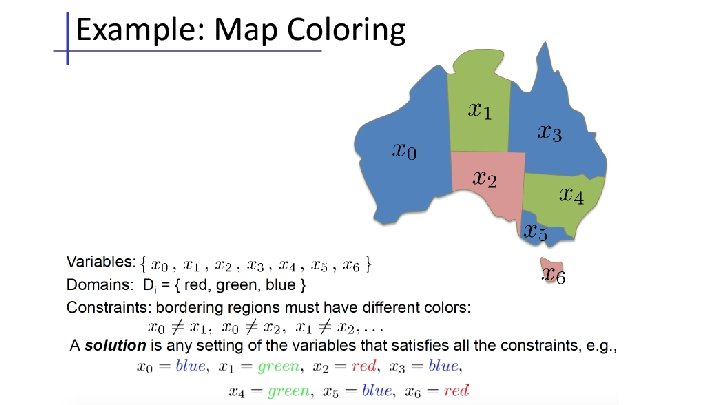
CSP

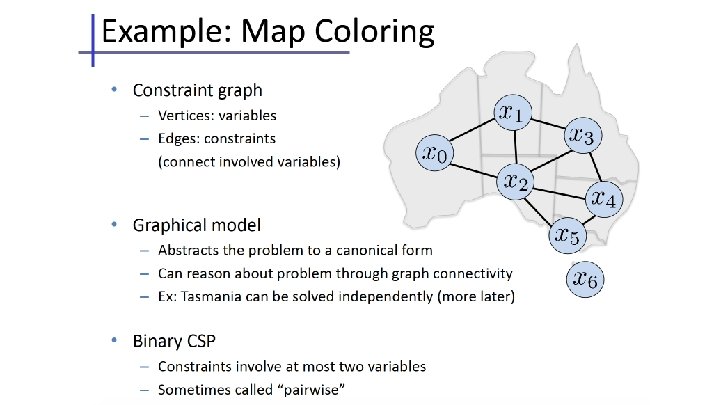
CSP





