II PROTEIN BIOCHEMISTRY 2 6 Enzyme Kinetics 2

II. PROTEIN BIOCHEMISTRY § 2. 6 Enzyme Kinetics § 2. 6 a Chemical Kinetics § 2. 6 b Michaelis-Menten Kinetics § 2. 6 c Enzyme-Inhibition Kinetics

§ 2. 6 a Chemical Kinetics

Synopsis 2. 6 a - Chemical kinetics (or reaction kinetics) is the study of rates of chemical reactions —enzyme kinetics is concerned with reactions catalyzed by enzymes! - Getting a good grasp of chemical kinetics is all about befriending algebra and calculus coupled with mastering the units of various parameters—to treat each parameter in terms of its SI units is the real trick here! - The square brackets [ ] enclosing a parameter are used to indicate either its concentration or units—the context provides the distinction! - The >> or << sign usually implies greater than or less than at least an order of magnitude! - Y is n orders of magnitude greater than X—what does this mean? : if n=1 => Y = 101. X => One order of magnitude if n=2 => Y = 102. X => Two orders of magnitude if n=3 => Y = 103. X => Three orders of magnitude The “order of magnitude” is expressed in terms of the logarithmic scale!

First-Order Reaction: The Rate Equation A k P - Consider the above reaction involving the decay of species A into P - Assuming that A decays into P with first-order kinetics, the reaction rates in terms of [A] or [P] at time t can be expressed as follows: d[A]/dt = -k[A] [1. 1] but: [A] = [A]0 - [P] [1. 2] thus: d[A]/dt = -k([A]0 -[P]) [1. 3] also: d[P]/dt = - d[A]/dt = k[A] = k([A]0 -[P]) [1. 4] where: [A]0 = Concentration @ time t=0 of reactant A [M] [A] = Concentration @ time t of reactant A [M] [P] = Concentration @ time t of reactant P [M] k = First-order rate constant (s-1) - In a first-order reaction, the reaction rate is simply proportional to the concentration of species A remaining or species P already formed at time t

First-Order Reaction: The Linear Plot - Integrating Eq[1. 1] with respect to t yields: d[A]/dt = -k[A] [1. 1] => ʃ d[A]/[A] = -k ʃdt => ln[A]-ln[A]0 = -kt => ln[A] = -kt + ln[A]0 [1. 5] ln[A] = -kt + ln[A]0 where [A]0 is the initial concentration of reactant A @ time zero (t 0) - Recall from calculus that: ʃ(1/x)dx = lnx - According to Eq[1. 5], a plot of ln[A] versus t will generate a straight line with: slope = -k y-intercept = ln[A]0 - Why the units of k are s-1? —from Eq[1. 1], we have: [k] = {[d[A]]/[dt]}. {1/[[A]]} [k] = {M/s}. {1/M} [k] = s-1 t

Second-Order Reaction: The Rate Equation A+L k P - Consider the above reaction involving the decay of species A and L into P - Assuming that the formation of P proceeds with second-order kinetics, the reaction rates in terms of [A] or [P] at time t can be expressed as follows: d[A]/dt = -k[A][L] [2. 1] assuming [A]=[L]: d[A]/dt = -k[A]2 [2. 2] but: [A] = [A]0 - [P] [2. 3] thus: d[A]/dt = -k([A]0 -[P])2 [2. 4] also: d[P]/dt = - d[A]/dt = k[A]2 = k([A]0 -[P])2 [2. 5] where: A]0 = Concentration @ time t=0 of reactant A [M] [A] = Concentration @ time t of reactant A [M] [L] = Concentration @ time t of reactant L (M) [P] = Concentration @ time t of reactant P [M] k = First-order rate constant (s-1) - In a second-order reaction, the reaction rate is simply proportional to the square of the concentration of species A remaining or species P already formed at time t

Second-Order Reaction: The Linear Plot - Integrating Eq[2. 2] with respect to t yields: d[A]/dt = -k[A][L] [2. 1] => ʃ d[A]/[A]2 = -k ʃdt => -1/[A] + 1/[A]0 = -kt => 1/[A] = kt + 1/[A]0 [2. 6] 1/[A] = kt + 1/[A]0 where [A]0 is the (initial) concentration of reactant A @ time zero (t 0) - Recall from calculus that: ʃ(1/x 2)dx = -(1/x) - According to Eq[2. 6], a plot of 1/[A] versus t will generate a straight line with: slope = k y-intercept = 1/[A]0 - Why the units of k are M-1 s-1? —from Eq[2. 2], we have: [k] = {[d[A]]/[dt]}. {1/[[A]2]} [k] = {M/s}. {1/M 2} [k] = M-1 s-1 t

Pseudo-First-Order Reaction: The Rate Equation A+L k Second-order P if: [L] >> [A] A k[L] P Pseudo-first-order - In the context of a second-order reaction scheme, let us assume that: [L] >> [A] - Under these conditions, the change in [L] is negligible over the course of reaction relative to change in [A]—in other words, the rate of the above reaction is primarily determined by [A] - Simply put, the second-order reaction (top left) will essentially behave like a first-order reaction (top right) - Kineticists refer to the above scenario as a “pseudo-first-order reaction” with a pseudo-firstorder rate constant (k’) given by the following relationship: k’ = k[L] [3. 1] with the units of k’ being s-1! Why? ! - The rate equation in terms of [A] at time t for the pseudo-first order reaction is analogous to the bona fide first-order reaction: d[A]/dt = -k’[A] [3. 2]

Pseudo-First-Order Reaction: The Exponential Plot - Integrating Eq[3. 2] with respect to t yields: d[A]/dt = -k[A][L] [3. 2] => ʃ d[A]/[A] = -k’ ʃdt => ln[A]-ln[A]0 = -k’t => ln[A] = -k’t + ln[A]0 [3. 3] [A]0 [A] = [A]0 exp(-k’t) Þ [A] = [A]0 e(-k’t) where: e = 2. 7182 - Taking anti-ln of both sides of Eq[3. 3] generates the corresponding exponential equation: ln[A] - ln[A]0 = -k’t => ln([A]/[A]0) = -k’t => [A]/[A]0 = exp(-k’t) => [A] = [A]0 exp(-k’t) [3. 4] [A] - According to Eq[3. 4], a plot of [A] vs t will generate an exponential decay curve—such plots are referred to as “exponential kinetics” - Exponential kinetics form the basis of enzyme kinetics and protein-ligand kinetics—the decay of a reactant into a product usually occurs in an exponential manner (doubling the time doubles the amount of product formed under nonlimiting concentrations of reactant )! t

Exercise 2. 6 a - Write the rate equation for a first-order and a second-order reaction - Express the first-order and the second-order rate constants in terms of SI units - What is a pseudo-first-order reaction? - What are exponential kinetics? - In terms of kinetics, who wins the race? Tortoise or hare?

§ 2. 6 b Michaelis-Menten Kinetics

Synopsis 2. 6 b - Michaelis-Menten kinetics describes a reaction scheme that best models the action of simple enzymes—eg that convert a single substrate into a product - In Michaelis-Menten model of enzyme kinetics, it is assumed that the enzymaticallycatalyzed reaction proceeds through two distinct steps: (1) An enzyme E binds a substrate (S) to form a transient (or intermediate) enzyme-substrate (ES) complex (2) The enzyme-substrate (ES) complex subsequently decays (or turns over) into the free enzyme (E) and a product (P) - The Michaelis-Menten rate equation is based on the so-called “steady-state assumption” —ie enzyme-catalyzed reactions operate under steady-state conditions wherein the rate of formation of ES complex (from E and S) equals its decay (into E and P) - How good is an enzyme at catalyzing a reaction is called the “catalytic efficiency”—this is expressed in terms of the kcat/KM quotient, where: kcat = the turnover number (or the catalytic constant) that is equal to the number of catalytic cycles per unit time—a measure of how good an enzyme is at turning a substrate over into a product! KM = the Michaelis constant (KM) that is equal to substrate concentration at which the enzyme attains its half-maximal velocity—a measure of how good an enzyme is at binding to its substrate (lower the KM, stronger the binding!)

Michaelis-Menten Kinetics: Reaction Scheme - In Michaelis-Menten kinetics, the conversion of a substrate (S) into product (P) by an enzyme (E) is proposed to proceed via an enzyme-substrate (ES) complex intermediate as embodied in the above reaction scheme - Let us define the concentrations—all expressed in the units of M (mol/L)—for the various reactants, intermediates and products as follows: Leonor Michaelis [E]0 = Free (total) enzyme concentration @ time t 0 (1875 -1949) [E] = Free (available) enzyme concentration @ time t [S] = Substrate concentration @ time t 0 [ES] = Enzyme-substrate complex concentration @ time t [P] = Product concentration @ time t [P]0 = Product concentration @ time t (during the initial burst phase) - With elementary kinetics under our belt, we can easily infer what the various rate constants are: k+1 = Second-order rate constant (M-1 s-1) k-1 = First-order rate constant (s-1) k+2 = First-order rate constant (s-1) k-2 = Second-order rate constant (M-1 s-1) - Since the reversible conversion of P to ES is negligible for the forward reaction, it is assumed that k+2 >> k-2 (contribution of k-2 is ignored!) Maud Menten (1879 -1960)

Michaelis-Menten Kinetics: Steady-State Assumption Progress Curves [S]0 - Given that the total enzyme (E 0) only exists in two states—either as free enzyme (E) or that bound to the substrate (ES)—we have the following relationship at time t in the reaction: [E]0 = [E] + [ES] [4. 1] - Next, assuming that k+2 >> k-2 (k-2 is negligible!), the rate of formation of ES at time t is given by: d[ES]/dt = k+1[E][S] – k-1[ES] – k+2[ES] [4. 2] - Given that [S] is not limiting or simply put [S] >> [E], [ES] remains more or less constant over the steady-state phase of the reaction (excluding the initial and final stages)—this is called the “steady-state assumption”— ie the rate of formation of [ES] equals its decay! - In calculus terms, we can express the steady-state assumption as: d[ES]/dt = 0 [4. 3] [E]0 = [E] + [ES] = = [E]0 - Such steady-state assumption is a hallmark of Michaelis -Menten kinetics! Steady-State Phase t

Michaelis-Menten Kinetics: Initial Velocity - Now, combining Eq[4. 2] and Eq[4. 3], we have: k+1[E][S] – k-1[ES] – k+2[ES] = 0 => k+1[E][S] = k-1[ES] + k+2[ES] [4. 4] - Next, we combine Eq[4. 1] with Eq[4. 4] so as to eliminate the variable [E]: k+1[S]. {[E]0 – [ES]} = k-1[ES] + k+2[ES] => {[S]/[ES]}. {[E]0 – [ES]} = (k-1 + k+2)/k+1 [4. 5] - For simplicity, the various rate constants on the right side of Eq[4. 5] can be treated as a single composite steady-state constant—designated KM—this is the Michaelis constant defined as: KM = (k-1 + k+2)/k+1 [4. 6] - Now, let us combine Eq[4. 5] and Eq[4. 6]: KM = {[S]/[ES]}. {[E]0 – [ES]} => KM[ES] = [S]. {[E]0 – [ES]} Determining v @ [S]=x 1 [4. 7] - Solving Eq[4. 7] for [ES] and multiplying both sides with k+2 yields: Slope = KM[ES] = [S][E]0 – [S][ES] [P] v => KM = {[S][E]0}/[ES] – [S] => KM + [S] = {[S][E]0}/[ES] => [ES] = {[S][E]0}/{KM + [S]} Initial burst phase => k+2[ES] = k+2{[S][E]0}/{KM + [S]} [4. 8] t - Now, the initial reaction rate or velocity (v) of the formation of product P can be expressed as (with [P]0 being the product concentration during the initial burst phase and the units of v being Ms-1): v = d[P]0/dt = k+2[ES] [4. 9]

Michaelis-Menten Kinetics: Michaelis-Menten Equation - Combining Eq[4. 8] and Eq[4. 9], we have: v = k+2{[S][E]0}/{KM + [S]} [4. 10] - The maximum reaction velocity (Vmax) occurs when the enzyme is fully saturated with substrate—ie when [ES] is no longer-rate-limiting and approaches [E]0: [ES] [E]0 - Thus, under such steady-state conditions, the reaction reaches Vmax solely determined by the product of k+2 and [E]0: Vmax = d[P]/dt = k+2[E]0 [4. 11] - Now, combining Eq[4. 10] and Eq[4. 11], we obtain: v = {Vmax[S]}/{KM + [S]} [4. 12] - Eq[4. 12] is the Michaelis-Menten equation that describes a hyperbola characteristic of substrates catalyzed by simple enzymes—ie a plot of v versus [S] —or the Michaelis-Menten Plot! - Can we determine the values of KM and Vmax from the Michaelis-Menten plot? If so, should we adapt this approach? Michaelis-Menten Plot

Michaelis-Menten Kinetics: Michaelis-Menten Plot - Assuming that v=Vmax/2, Eq[4. 12] reduces to: Vmax/2 = {Vmax[S]}/{KM + [S]} => KM + [S] = 2[S] => KM = [S] [4. 13] - Simply put, KM is the value of [S] @ v=Vmax/2—ie KM is indicative of the affinity of an enzyme for a substrate— the lower the KM, the greater the affinity! - Accordingly, from a Michaelis-Menten plot, one COULD directly determine the values of KM and Vmax using a least-squares fit of the experimental data points to Eq[4. 12] - Thus, KM (M) would be the value of [S] @ Vmax/2, and Vmax (Ms-1) the value of v when the curve plateaus out— but, where exactly does the curve plateau out? !!! - Although the curve asymptotically approaches Vmax @ very high values of [S], accurate determination of Vmax is still far from certain - Because of such uncertainty, we LINEARIZE Eq[4. 12] to determine the values of KM and Vmax—enter the Lineweaver-Burk plot! Michaelis-Menten Plot

Michaelis-Menten Kinetics: Lineweaver-Burk Plot - Reciprocating both sides of Eq[4. 12], we obtain: 1/v = {KM + [S]}/{Vmax[S]} => 1/v = {KM/(Vmax[S])} + {[S]/(Vmax[S])} => 1/v = (KM/Vmax). (1/[S]) + (1/Vmax) [4. 14] => y= (m). (x) + (b) - Eq[4. 14] is the equation of a straight line—it is called the Lineweaver-Burk equation - Thus, a plot of 1/v versus 1/[S] generates a straight line from which the various kinetic parameters can be accurately determined using a linear fit with: slope = KM/Vmax y-intercept = 1/Vmax x-intercept = -1/KM - When 1/v=0 (in order to determine the x-intercept), Eq[4. 14] reduces to: 0 = (KM/Vmax). (1/[S]) + (1/Vmax) => (KM/Vmax). (1/[S]) = -(1/Vmax) => KM. (1/[S]) = -1 => 1/[S] = -1/KM [4. 15] - The double-reciprocal plot of 1/v versus 1/[S] is called the Lineweaver-Burk plot Lineweaver-Burk Plot 1/v

Michaelis-Menten Kinetics: Catalytic Constant - In order to assess the catalytic efficiency of an enzyme, a parameter called the catalytic constant (kcat) is defined as follows (with the units of kcat being s-1): kcat = Vmax/[E]0 [4. 16] - Now, combining Eq[4. 11] and Eq[4. 16], tells us that kcat is the first-order rate constant (k+2) associated with the decay of ES into P and E—an inherent consequence of steadystate assumption: kcat[E]0 = k+2[E]0 => kcat = k+2 [4. 17] - Thus, kcat is essentially the number of reaction turnovers or catalytic cycles per unit time accomplished by a particular enzyme—hence, kcat is also referred to as the “turnover number” - But, kcat only tells us how good an enzyme is @ turning over the substrate after it is already bound to the active site—it tells us nothing about how good an enzyme is @ binding the substrate for if this cannot occur efficiently, substrate binding would become the rate-limiting step and diminish the overall performance of the enzyme even if kcat is working @ supersonic speed! - So what else do we need beside kcat to accurately determine the catalytic efficiency of an enzyme? What kinetic parameter determines how good an enzyme is @ binding the substrate? Would KM suffice? If so, what do we do with it?

Michaelis-Menten Kinetics: Catalytic Efficiency - During the initial “burst” phase of the reaction when [S] << KM, we can say that: KM + [S] KM [4. 18] - Additionally, during the initial “burst” phase of the reaction, the amount of free enzyme available is virtually the same Slope = as the amount of enzyme initially added, or simply put: [P] v [E]0 [4. 19] - Thus, combining Eq[4. 18] and Eq[4. 19] with Eq[4. 10], we have: v = k+2{[S][E]}/KM v = (kcat/KM). [S][E] [4. 20] Initial burst phase t - Eq[4. 20] is a second-order reaction with kcat/KM quotient being the second-order rate constant with units of M-1 s-1 - The kcat/KM parameter is an indicator of the overall catalytic efficiency—ie how efficiently an enzyme converts a substrate into product - Given that the catalytic efficiency will eventually reach an upper limit due to the limitation of substrate and product molecules to diffuse in and out of the enzyme active site (particularly within the highly viscous milieu of the living cell), the kcat/KM parameter unsurprisingly displays the diffusion-controlled limit of about 109 M-1 s-1—some enzymes can however operate in excess of this limit via the so-called quantum tunneling!

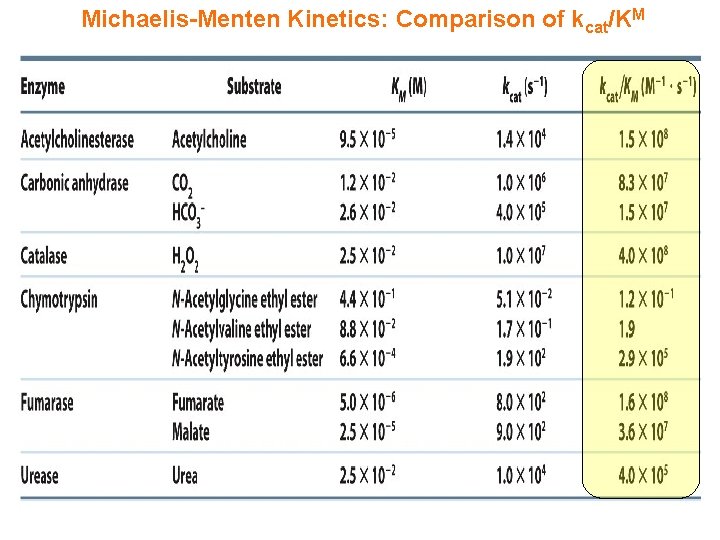
Michaelis-Menten Kinetics: Comparison of kcat/KM

Exercise 2. 6 b - What are the differences between initial velocity, and maximum velocity for an enzymatic reaction? - Derive the Michaelis–Menten equation. Show the workout and reasoning behind each assumption. - What do the values of KM and kcat/KM reveal about an enzyme? - Why an enzyme cannot have a kcat/KM value greater than 109 M– 1 s– 1? - Write the Lineweaver–Burk equation and describe the features of a Lineweaver–Burk plot

§ 2. 6 c Enzyme-Inhibition Kinetics

Synopsis 2. 6 c - Enzyme inhibition is central to understanding the action of drugs on enzymes - Enzyme inhibitors (eg drugs) interact reversibly or irreversibly with an enzyme to alter its KM and/or Vmax values—such inhibitors can be classified into three types: competitive, uncompetitive and mixed (or noncompetitive) - A competitive inhibitor competes with the substrate (S) for binding to the free enzyme (E)—it increases the KM but has no effect on the Vmax - An uncompetitive inhibitor binds only to enzyme-substrate (ES) complex and does NOT compete with the substrate (S) for binding to the free enzyme (E)—it decreases both the KM and Vmax - A mixed inhibitor competes with the substrate (S) for binding to the free enzyme (E) but uncompetitively binds to the enzyme-substrate (ES) complex—it decreases the Vmax but KM may increase or decrease - A noncompetitive inhibitor is a mixed inhibitor that indiscriminately or noncompetitively binds to both the free enzyme (E) and the enzyme-substrate (ES) complex with an equal affinity—it decreases the Vmax but has no effect on KM - In short, enzyme inhibition can be divided into THREE categories: (1) Competitive Inhibition (2) Uncompetitive Inhibition (3) Mixed Inhibition

(1) Competitive Inhibition: General Model - In competitive inhibition, an inhibitor usually resembles the substrate—it is a chemical analogue of the substrate and exerts its action by binding to the active site! - Thus, a competitive inhibitor (I) directly competes with the substrate (S) for the active site of the free enzyme (E)—but cannot be converted to a product (P)—thereby essentially acting as a ligand to sterically block substrate binding - In the generalized model shown, EI is the catalytically-inactive enzyme-inhibitor complex—the equilibrium dissociation constant (KI) associated with the formation of EI is given by: KI = [E][I]/[EI] [1. 1] where [E] = Concentration (M) of freely available enzyme @ equilibrium [I] = Concentration (M) of freely available inhibitor @ equilibrium [EI] = Concentration (M) of enzyme-inhibitor complex @ equilibrium

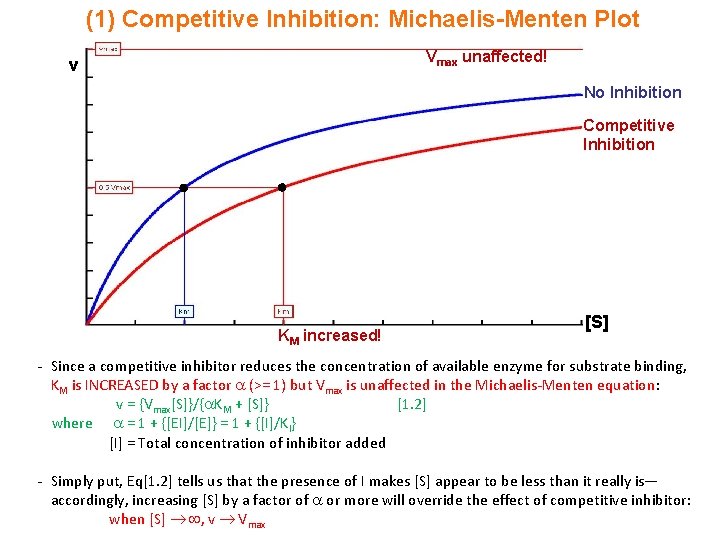
(1) Competitive Inhibition: Michaelis-Menten Plot Vmax unaffected! v No Inhibition Competitive Inhibition KM increased! [S] - Since a competitive inhibitor reduces the concentration of available enzyme for substrate binding, KM is INCREASED by a factor (>= 1) but Vmax is unaffected in the Michaelis-Menten equation: v = {Vmax[S]}/{ KM + [S]} [1. 2] where = 1 + {[EI]/[E]} = 1 + {[I]/KI} [I] = Total concentration of inhibitor added - Simply put, Eq[1. 2] tells us that the presence of I makes [S] appear to be less than it really is— accordingly, increasing [S] by a factor of or more will override the effect of competitive inhibitor: when [S] , v Vmax

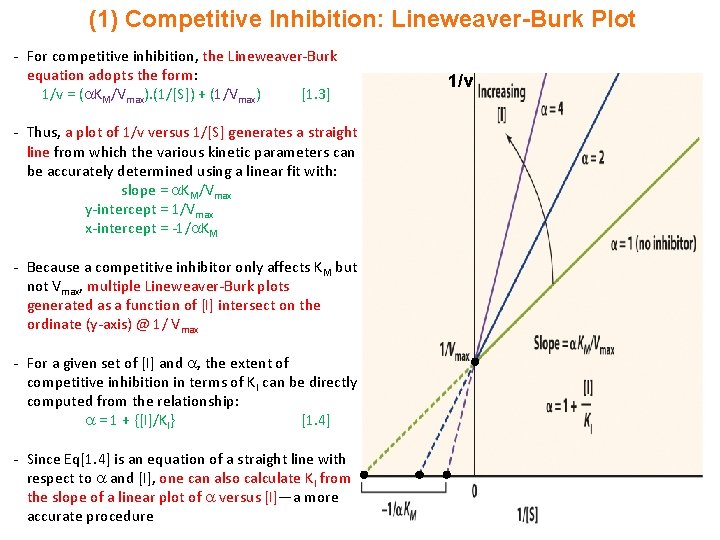
(1) Competitive Inhibition: Lineweaver-Burk Plot - For competitive inhibition, the Lineweaver-Burk equation adopts the form: 1/v = ( KM/Vmax). (1/[S]) + (1/Vmax) [1. 3] - Thus, a plot of 1/v versus 1/[S] generates a straight line from which the various kinetic parameters can be accurately determined using a linear fit with: slope = KM/Vmax y-intercept = 1/Vmax x-intercept = -1/ KM - Because a competitive inhibitor only affects KM but not Vmax, multiple Lineweaver-Burk plots generated as a function of [I] intersect on the ordinate (y-axis) @ 1/ Vmax - For a given set of [I] and , the extent of competitive inhibition in terms of KI can be directly computed from the relationship: = 1 + {[I]/KI} [1. 4] - Since Eq[1. 4] is an equation of a straight line with respect to and [I], one can also calculate KI from the slope of a linear plot of versus [I]—a more accurate procedure 1/v

(2) Uncompetitive Inhibition: General Model - In uncompetitive (NOT noncompetitive!) inhibition, an uncompetitive inhibitor (I) directly binds to the enzyme-substrate (ES) complex but NOT to the free enzyme (E) - While it may or may not resemble the substrate, an uncompetitive inhibitor exerts its effect by virtue of its ability to distort the enzyme active site so as to render it catalytically-inactive—the inhibitor must bind at an allosteric site located away from the active site! - In the generalized model shown, ESI is the catalytically-inactive enzyme-substrate-inhibitor complex— the equilibrium dissociation constant (K’I) associated with the formation of ESI is given by: K’I = [ES][I]/[ESI] [2. 1] where [ES] = Concentration (M) of freely available ES complex @ equilibrium [I] = Concentration (M) of freely available inhibitor @ equilibrium [ESI] = Concentration (M) of ESI complex @ equilibrium

(2) Uncompetitive Inhibition: Michaelis-Menten Plot v No Inhibition Vmax reduced! Uncompetitive Inhibition [S] KM reduced! - Since an uncompetitive inhibitor reduces the concentration of ES complex available for product generation, both KM and Vmax are DECREASED by a factor ’ (>= 1) in the Michaelis-Menten equation: v = {(Vmax/ ’)[S]}/{(KM/ ’)+ [S]} [2. 2] where ’ = 1 + {[ESI]/[ES]} = 1 + {[I]/K’I} [I] = Total concentration of inhibitor added! - Eq[2. 2] tells us that while uncompetitive inhibition reduces both KM and Vmax by a factor ’, it does not affect the overall KM/Vmax quotient! - Unlike competitive inhibition, increasing [S] does NOT reverse the effect of an uncompetitive inhibitor!

(2) Uncompetitive Inhibition: Lineweaver-Burk Plot - For uncompetitive inhibition, the Lineweaver-Burk equation adopts the form: 1/v = (KM/Vmax). (1/[S]) + ( ’/Vmax) [2. 3] - Thus, a plot of 1/v versus 1/[S] generates a straight line from which the various kinetic parameters can be accurately determined using a linear fit with: slope = KM/Vmax y-intercept = ’/Vmax x-intercept = - ’/KM - Because an uncompetitive inhibitor does NOT affect the KM/Vmax quotient, multiple Lineweaver. Burk plots generated as a function of [I] harbor the same slope—they never intersect either @ abscissa (x-axis) or ordinate (y-axis) - For a given set of [I] and ’, the extent of uncompetitive inhibition in terms of K’I can be directly computed from the relationship: ’ = 1 + {[I]/K’I} [2. 4] - Since Eq[2. 4] is an equation of a straight line with respect to ’ and [I], one can also calculate K’I from the slope of a linear plot of ’ versus [I]—a more accurate procedure 1/v

(3) Mixed Inhibition: General Model - In mixed (or noncompetitive) inhibition, a mixed inhibitor (I) binds to both free enzyme (E) and enzymesubstrate (ES) complex—it has characteristics of both the competitive and uncompetitive inhibition! - While it may or may not resemble the substrate, a mixed inhibitor exerts its effect by virtue of its ability to not only block substrate binding but also distorting the enzyme active site so as to render it catalytically-inactive—the inhibitor must bind at an allosteric site located away from the active site! - In the generalized model shown, EI is the catalytically-inactive EI complex, and ESI is the catalyticallyinactive enzyme-substrate-inhibitor complex—the equilibrium dissociation constants (KI and K’I) respectively associated with the formation of EI and ESI are given by: KI = [E][I]/[EI] [3. 1] K’I = [ES][I]/[ESI] [3. 2] where [E] = Concentration (M) of freely available enzyme @ equilibrium [ES] = Concentration (M) of freely available ES complex @ equilibrium [I] = Concentration (M) of freely available inhibitor @ equilibrium [EI] = Concentration (M) of EI complex @ equilibrium [ESI] = Concentration (M) of ESI complex @ equilibrium

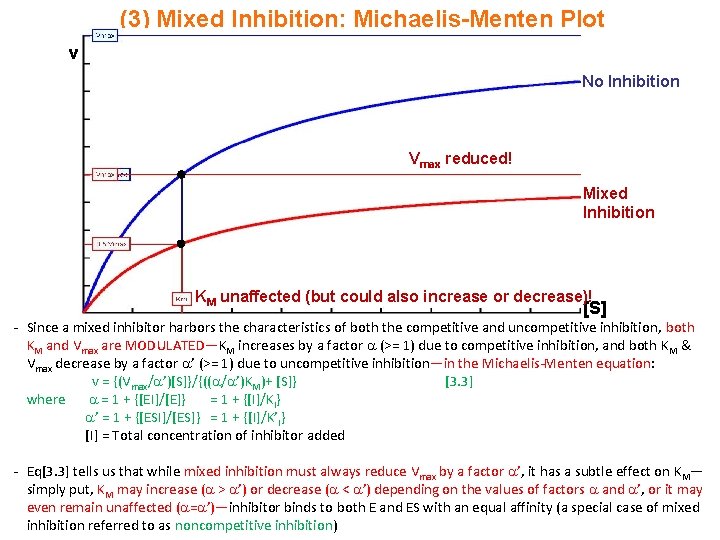
(3) Mixed Inhibition: Michaelis-Menten Plot v No Inhibition Vmax reduced! Mixed Inhibition KM unaffected (but could also increase or decrease)! [S] - Since a mixed inhibitor harbors the characteristics of both the competitive and uncompetitive inhibition, both KM and Vmax are MODULATED—KM increases by a factor (>= 1) due to competitive inhibition, and both KM & Vmax decrease by a factor ’ (>= 1) due to uncompetitive inhibition—in the Michaelis-Menten equation: v = {(Vmax/ ’)[S]}/{(( / ’)KM)+ [S]} [3. 3] where = 1 + {[EI]/[E]} = 1 + {[I]/KI} ’ = 1 + {[ESI]/[ES]} = 1 + {[I]/K’I} [I] = Total concentration of inhibitor added - Eq[3. 3] tells us that while mixed inhibition must always reduce Vmax by a factor ’, it has a subtle effect on KM— simply put, KM may increase ( > ’) or decrease ( < ’) depending on the values of factors and ’, or it may even remain unaffected ( = ’)—inhibitor binds to both E and ES with an equal affinity (a special case of mixed inhibition referred to as noncompetitive inhibition)

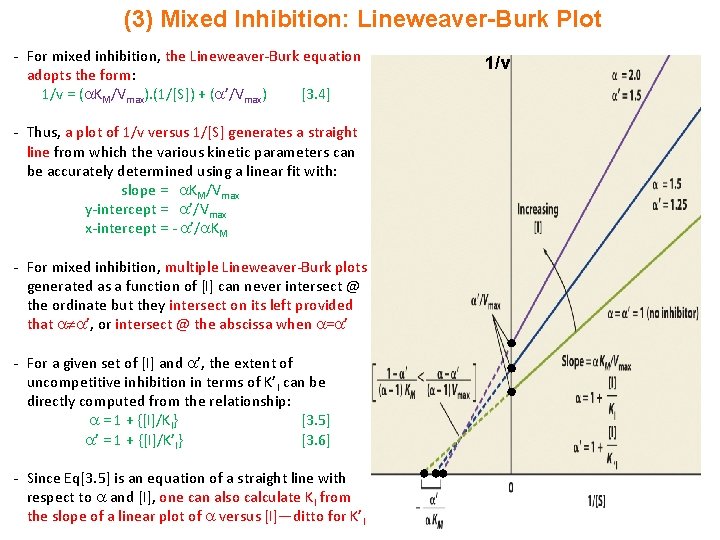
(3) Mixed Inhibition: Lineweaver-Burk Plot - For mixed inhibition, the Lineweaver-Burk equation adopts the form: 1/v = ( KM/Vmax). (1/[S]) + ( ’/Vmax) [3. 4] - Thus, a plot of 1/v versus 1/[S] generates a straight line from which the various kinetic parameters can be accurately determined using a linear fit with: slope = KM/Vmax y-intercept = ’/Vmax x-intercept = - ’/ KM - For mixed inhibition, multiple Lineweaver-Burk plots generated as a function of [I] can never intersect @ the ordinate but they intersect on its left provided that ’, or intersect @ the abscissa when = ’ - For a given set of [I] and ’, the extent of uncompetitive inhibition in terms of K’I can be directly computed from the relationship: = 1 + {[I]/KI} [3. 5] ’ = 1 + {[I]/K’I} [3. 6] - Since Eq[3. 5] is an equation of a straight line with respect to and [I], one can also calculate KI from the slope of a linear plot of versus [I]—ditto for K’I 1/v

Enzyme Inhibition: Comparison of Mechanisms

Exercise 2. 6 c - Why might an enzyme’s substrate, transition state, and product all serve as starting points for the design of a competitive inhibitor? - Describe the effects of competitive, uncompetitive, and mixed inhibitors on KM and Vmax - How can inhibitor binding to an enzyme be quantified?