Factoring and Testing Primes in Small Space Viliam

Factoring and Testing Primes in Small Space Viliam Geffert P. J. Šafárik University, Košice, Slovakia Dana Pardubská Comenius University, Bratislava, Slovakia

Factoring and Testing Primes in Small Space Viliam Geffert P. J. Šafárik University, Košice, Slovakia Dana Pardubská Comenius University, Bratislava, Slovakia

n is a prime

n is a prime if it cannot evenly be divided by any number other than 1 and itself

n is a prime if it cannot evenly be divided by any number other than 1 and itself Euclid [280 B. C. ]: infinite number of primes

n is a prime if it cannot evenly be divided by any number other than 1 and itself Euclid [280 B. C. ]: infinite number of primes J. Hadamard, C. J. de la Valée Poussin [1896]:

n is a prime if it cannot evenly be divided by any number other than 1 and itself Euclid [280 B. C. ]: infinite number of primes J. Hadamard, C. J. de la Valée Poussin [1896]: Prime Number Theorem

n is a prime if it cannot evenly be divided by any number other than 1 and itself Euclid [280 B. C. ]: infinite number of primes J. Hadamard, C. J. de la Valée Poussin [1896]: Prime Number Theorem pm = (1 + o(1)). m. ln m - pm denotes the m-th prime

Fundamental Theorem of Arithmetic - Factoring n = pi 1 ki. pi 2 ki. …. piℓki 1 2 ℓ kij > 0, integer

Fundamental Theorem of Arithmetic - Factoring n = pi 1 ki. pi 2 ki. …. piℓki 1 2 ℓ kij > 0, integer Factoring is computationally very hard

Fundamental Theorem of Arithmetic - Factoring n = pi 1 ki. pi 2 ki. …. piℓki 1 2 ℓ kij > 0, integer Factoring is computationally very hard - utilized to design secure cryptographic systems (data transmission over internet)

Primes = { n | n is a prime } - n binary coded

Primes = { n | n is a prime } - n binary coded un-Primes = {1 n | n is a prime }

Primes = { n | n is a prime } - n binary coded un-Primes = {1 n | n is a prime } Agrawal, Kayal, Saxena [2004]: Primes ϵ P

Primes = { n | n is a prime } - n binary coded un-Primes = {1 n | n is a prime } Agrawal, Kayal, Saxena [2004]: Primes ϵ P - no factorization, if n is composite

Primes = { n | n is a prime } - n binary coded un-Primes = {1 n | n is a prime } Agrawal, Kayal, Saxena [2004]: Primes ϵ P - no factorization, if n is composite P. Shor [1994]: polynomial time quantum algorithm for factoring

Primes = { n | n is a prime } - n binary coded un-Primes = {1 n | n is a prime } Agrawal, Kayal, Saxena [2004]: Primes ϵ P - no factorization, if n is composite P. Shor [1994]: polynomial time quantum algorithm for factoring How much space is sufficient?

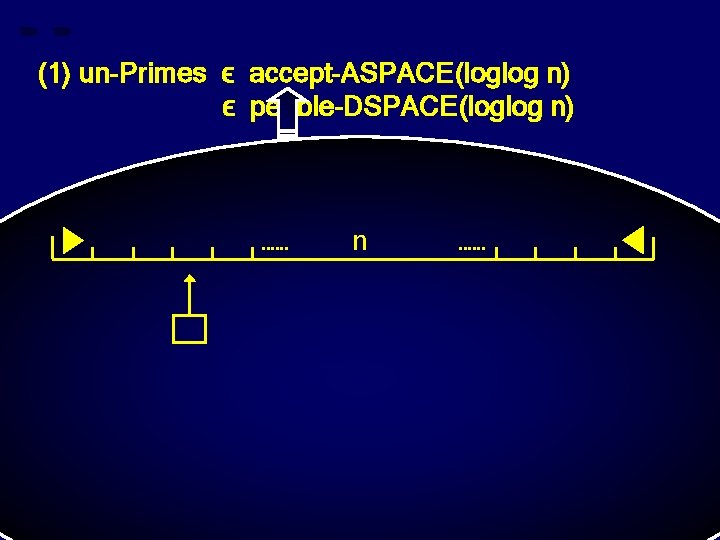
(1) un-Primes ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n)

(1) un-Primes ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n) n

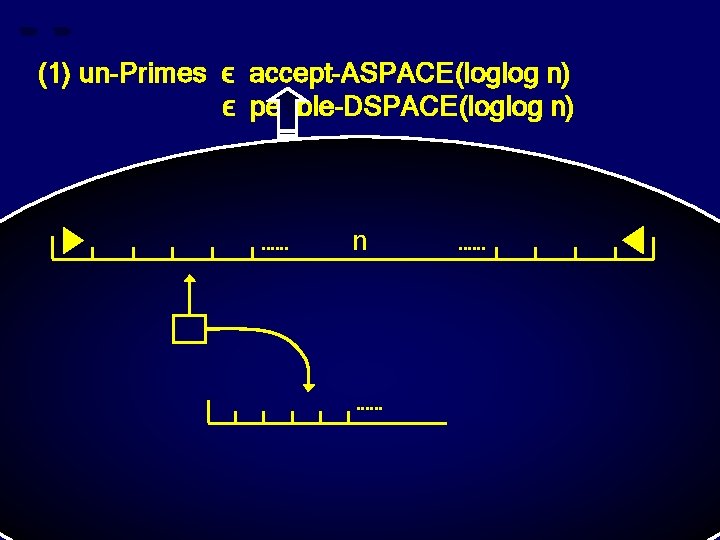
(1) un-Primes ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n) n

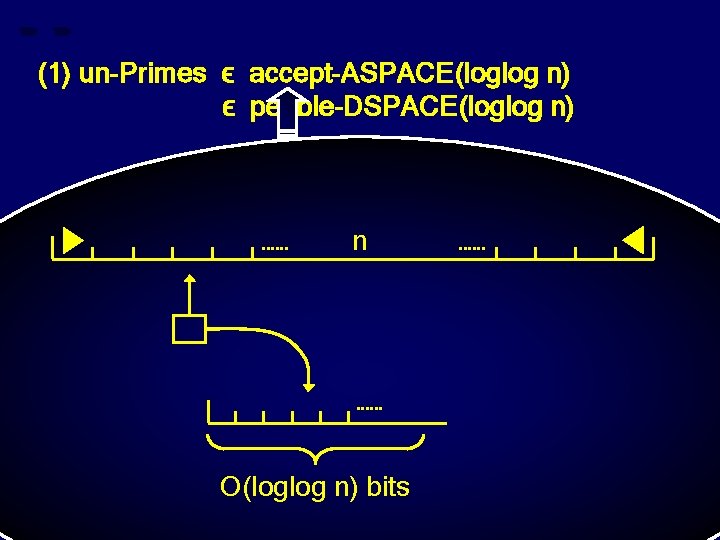
(1) un-Primes ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n) n

(1) un-Primes ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n) n O(loglog n) bits

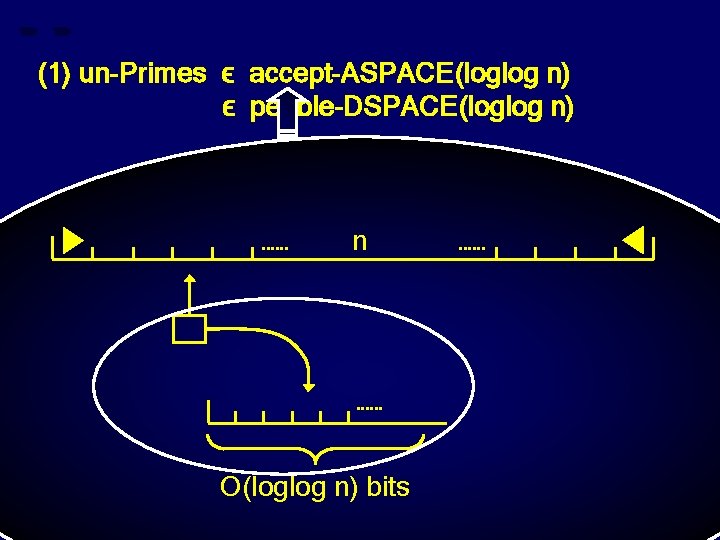
(1) un-Primes ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n) n O(loglog n) bits

(1) un-Primes ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n)

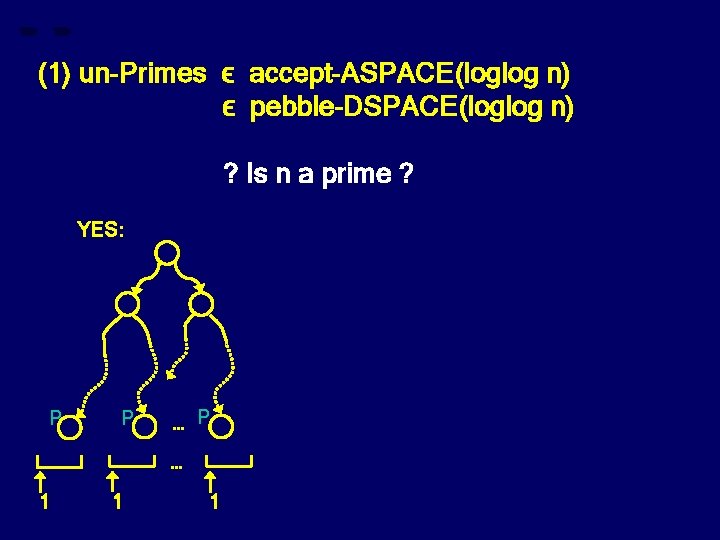
(1) un-Primes ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n) ? Is n a prime ? YES: P P … 1 1 1

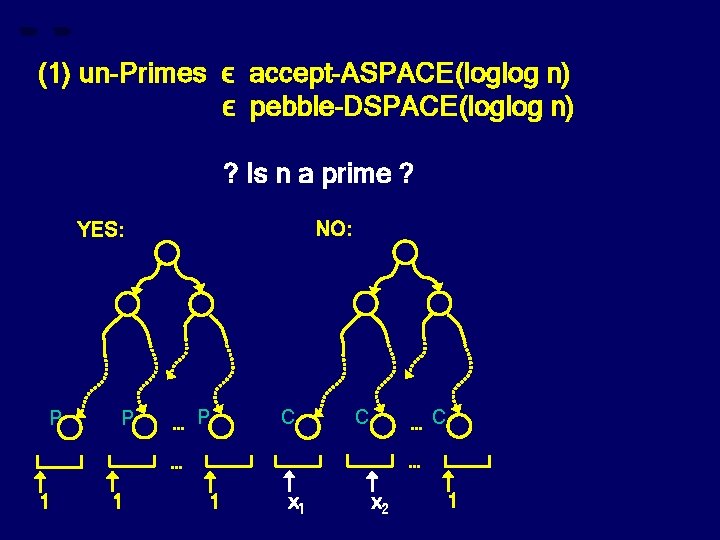
(1) un-Primes ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n) ? Is n a prime ? NO: YES: P P … P C C … … 1 1 1 x 2 1

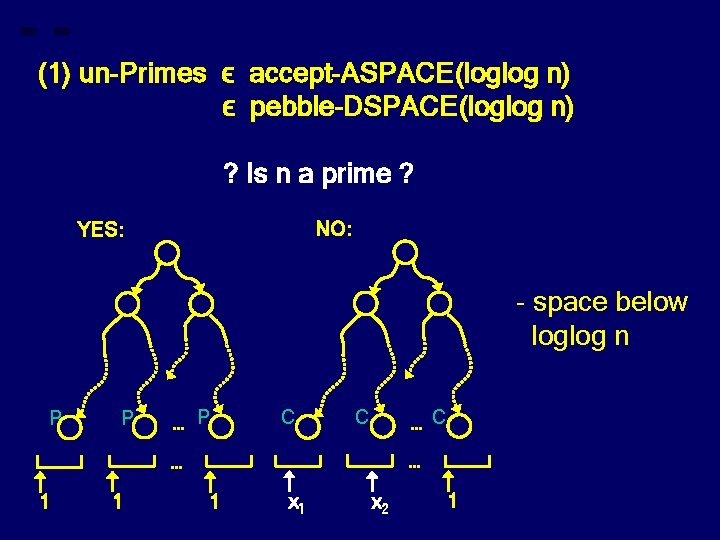
(1) un-Primes ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n) ? Is n a prime ? NO: YES: - space below loglog n P P … P C C … … 1 1 1 x 2 1

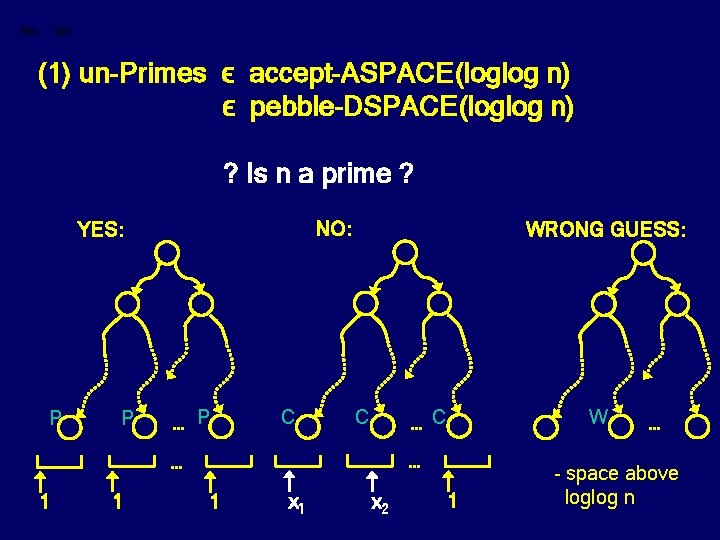
(1) un-Primes ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n) ? Is n a prime ? NO: YES: P P … P C WRONG GUESS: C … … 1 1 W 1 x 2 1 … - space above loglog n

(1) un-Primes ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n)

(1) un-Primes ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n) (2) un-Composites ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n)

(1) un-Primes ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n) (2) un-Composites ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n) - (2) is not a trivial consequence of (1), since it is not known whether ASPACE(loglog n) is closed under complement

(1) un-Primes ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n) (2) un-Composites ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n) - (2) is not a trivial consequence of (1), since it is not known whether ASPACE(loglog n) is closed under complement - additional bonus - factoring

Algorithm based on “elementary school” primality testing: for X = 2, 3, . . . , n-1 do if X divides n then “n is composite” end “n is prime”

O(loglog n) space due to

O(loglog n) space due to - Modular representation (based on Chinese Remainder Theorem)

O(loglog n) space due to - Modular representation (based on Chinese Remainder Theorem) M = p 1. p 2. …. pm n = (z 1, …, zm) , zi = n mod pi

O(loglog n) space due to - Modular representation (based on Chinese Remainder Theorem) M = p 1. p 2. …. pm n = (z 1, …, zm) , zi = n mod pi memory space: log pm O(loglog n)

O(loglog n) space due to - Modular representation (based on Chinese Remainder Theorem) M = p 1. p 2. …. pm n = (z 1, …, zm) , zi = n mod pi memory space: log pm O(loglog n) - Scalar representation

O(loglog n) space due to - Modular representation (based on Chinese Remainder Theorem) M = p 1. p 2. …. pm n = (z 1, …, zm) , zi = n mod pi memory space: log pm O(loglog n) - Scalar representation n = α. M , α ϵ 0, 1)

O(loglog n) space due to - Modular representation (based on Chinese Remainder Theorem) M = p 1. p 2. …. pm n = (z 1, …, zm) , zi = n mod pi memory space: log pm O(loglog n) - Scalar representation n = α. M , α ϵ 0, 1) -- truncated to 3. loglog n bits

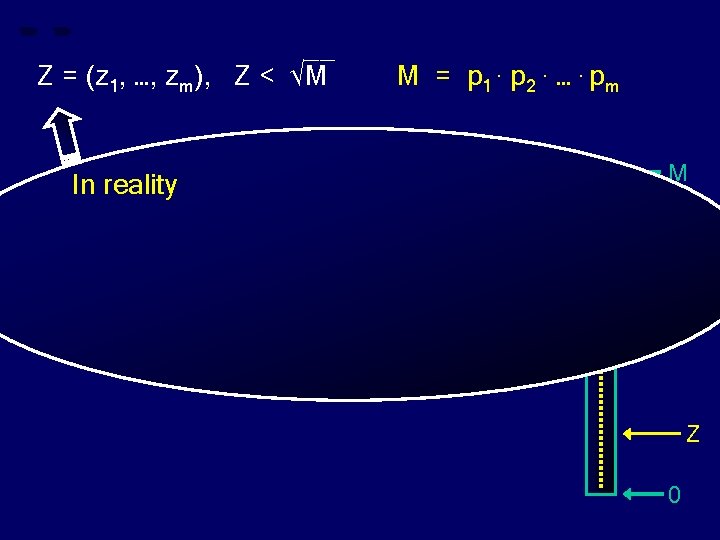
__ Z = (z 1, …, zm), Z < √M In reality M = p 1. p 2. …. pm M Z 0

__ Z = (z 1, …, zm), Z < √M M = p 1. p 2. …. pm M In reality Z Z 0

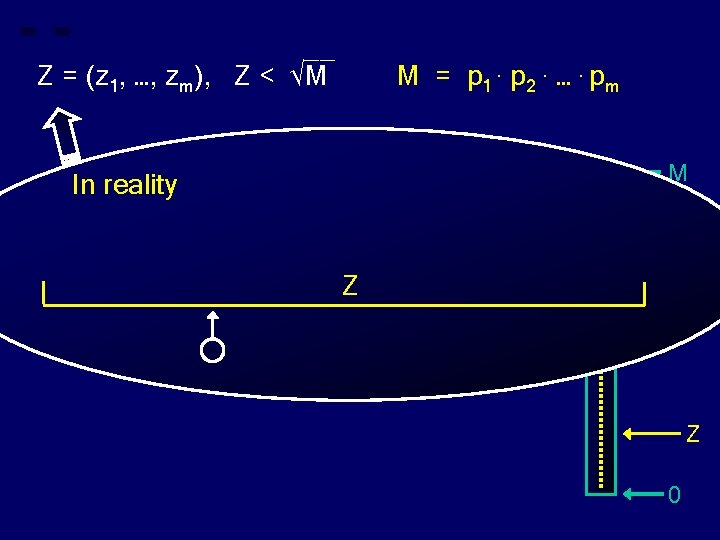
__ Z = (z 1, …, zm), Z < √M m O(log Z) M = p 1. p 2. …. pm M Z 0

__ Z = (z 1, …, zm), Z < √M M = p 1. p 2. …. pm m O(log Z) M pm O(m. log m) O(log Z. loglog Z) Z 0

__ Z = (z 1, …, zm), Z < √M M = p 1. p 2. …. pm m O(log Z) M pm O(m. log m) O(log Z. loglog Z) log pm O(loglog Z) Z 0

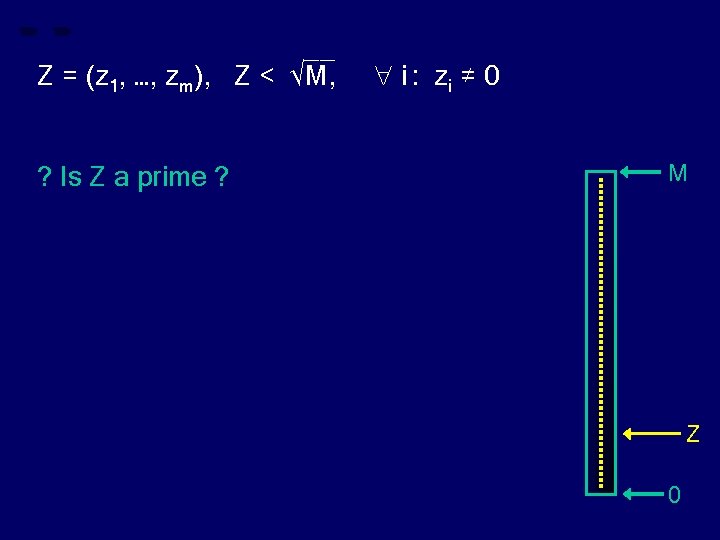
__ Z = (z 1, …, zm), Z < √M ? Is Z a prime ? M = p 1. p 2. …. pm M Z 0

__ Z = (z 1, …, zm), Z < √M M = p 1. p 2. …. pm ? Is Z a prime ? M if zi = 0 then “Z is a composite” Z 0

__ Z = (z 1, …, zm), Z < √M, ? Is Z a prime ? i : zi ≠ 0 M Z 0

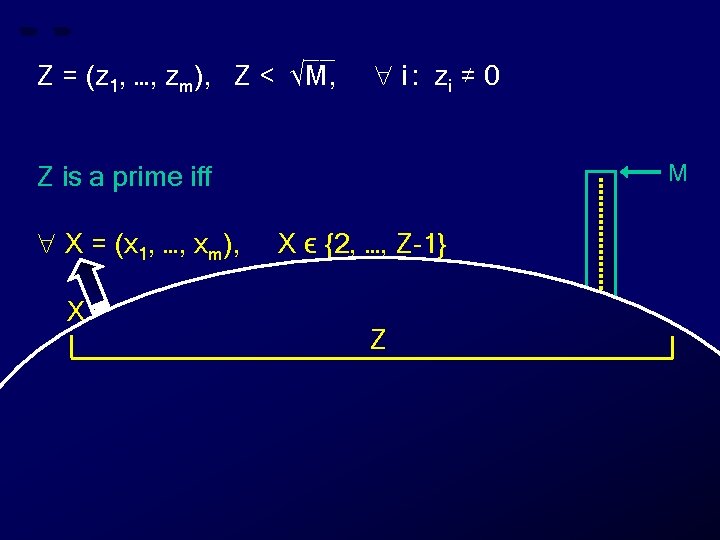
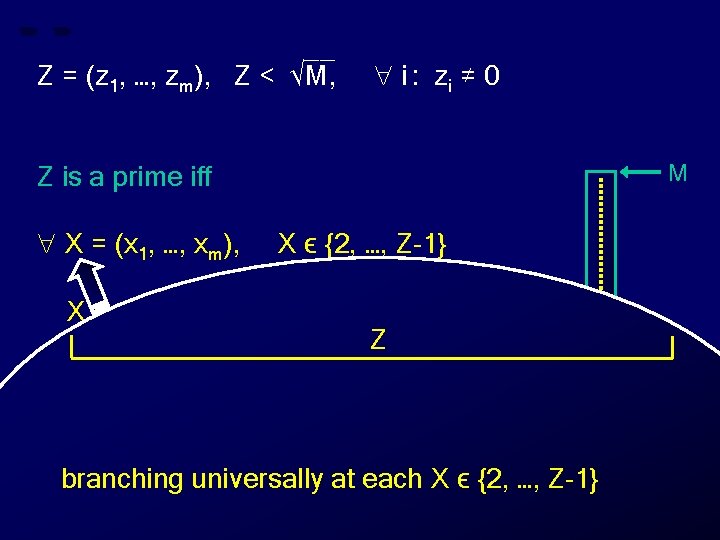
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 M Z is a prime iff X = (x 1, …, xm), X ϵ {2, …, Z-1} X does not divide Z Z 0 X

__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 M Z is a prime iff X = (x 1, …, xm), X ϵ {2, …, Z-1} X does not divide Z Z Z 0 X

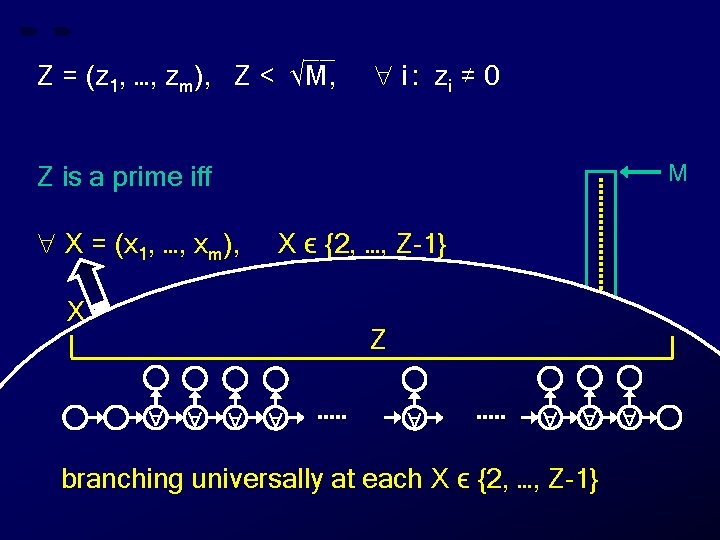
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 M Z is a prime iff X = (x 1, …, xm), X ϵ {2, …, Z-1} X does not divide Z Z Z branching universally at each X ϵ {2, …, Z-1} 0 X

__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 M Z is a prime iff X = (x 1, …, xm), X ϵ {2, …, Z-1} X does not divide Z branching universally at each X ϵ {2, …, Z-1} Z 0 X

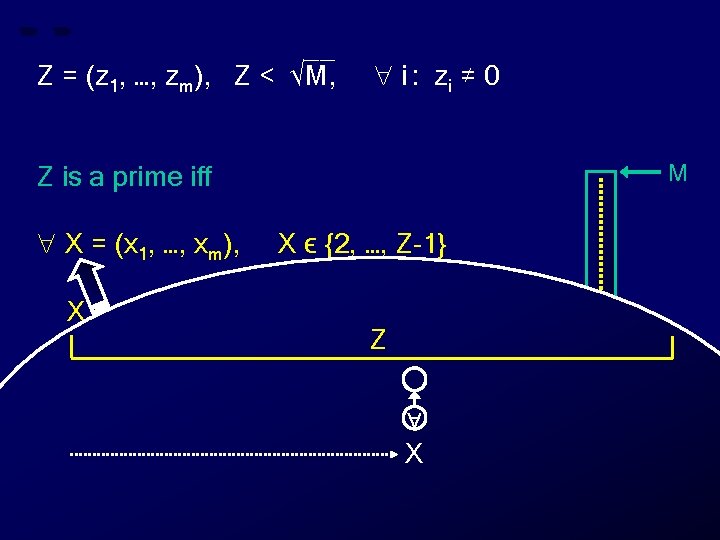
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 M Z is a prime iff X = (x 1, …, xm), X ϵ {2, …, Z-1} X does not divide Z Z Z X 0 X

__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 M Z is a prime iff X = (x 1, …, xm), X ϵ {2, …, Z-1} X does not divide Z Z 0 X

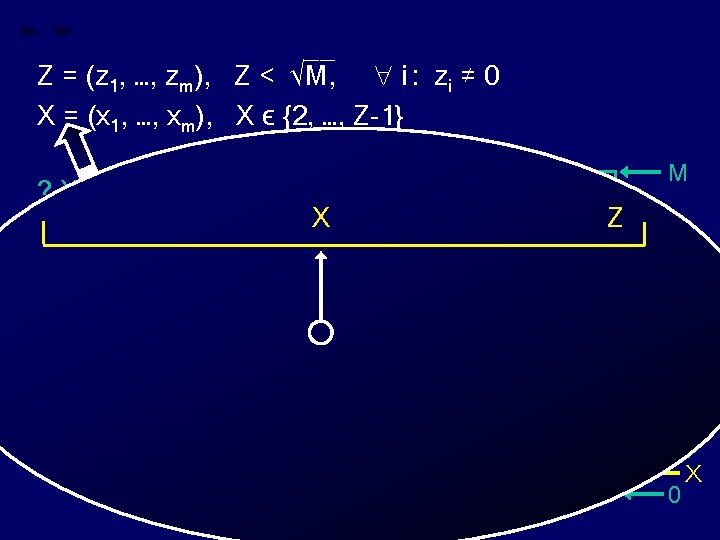
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} ? X divides Z ? M if xi = 0 then “X does not divide Z” Z 0 X

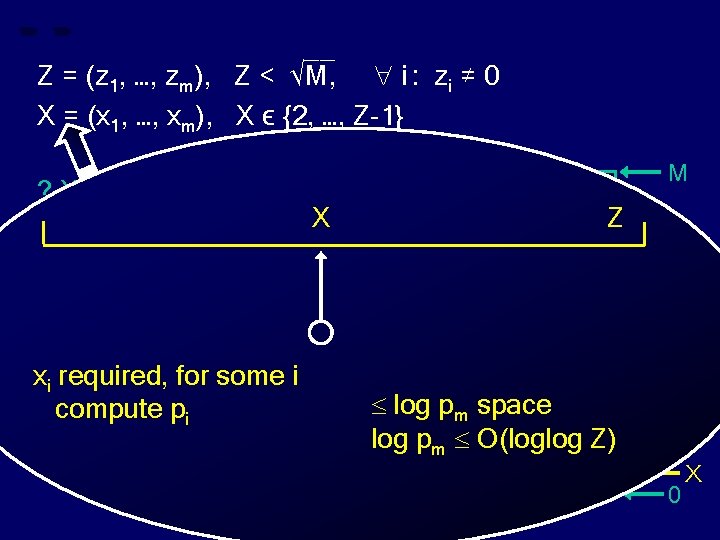
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} ? X divides Z ? M X Z xi required, for some i Z 0 X

__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} ? X divides Z ? xi required, for some i compute pi M X Z log pm space log pm O(loglog Z) Z 0 X

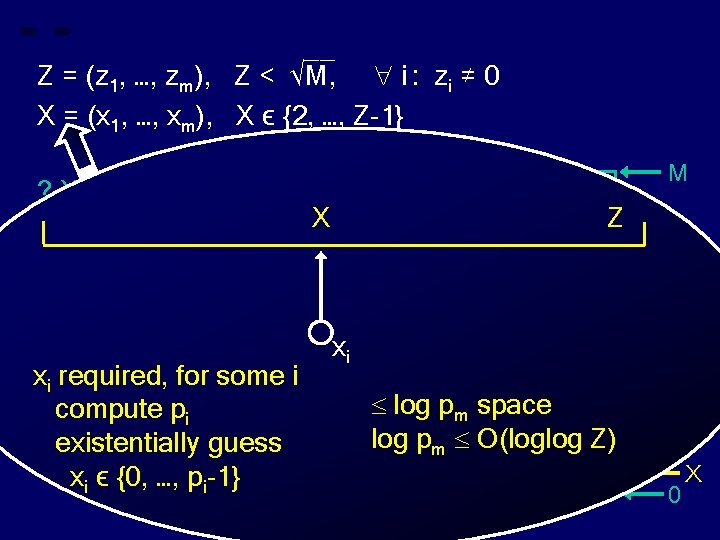
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} ? X divides Z ? xi required, for some i compute pi existentially guess xi ϵ {0, …, pi-1} M X Z xi log pm space log pm O(loglog Z) Z 0 X

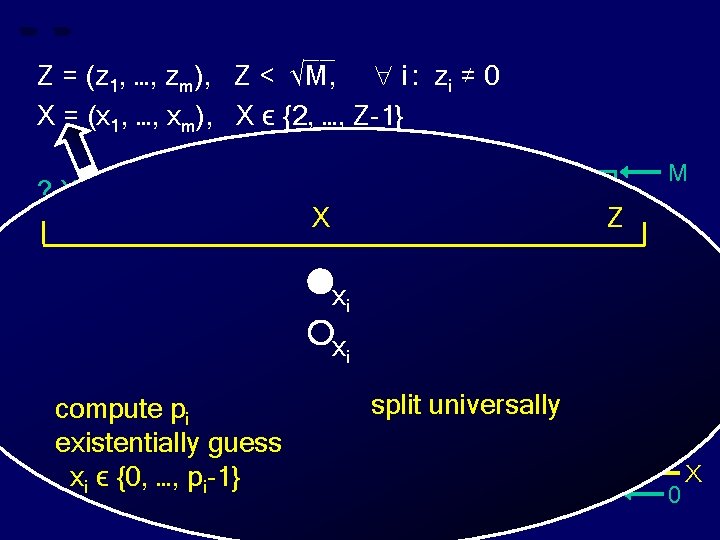
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} ? X divides Z ? M X Z xi xi compute pi existentially guess xi ϵ {0, …, pi-1} split universally Z 0 X

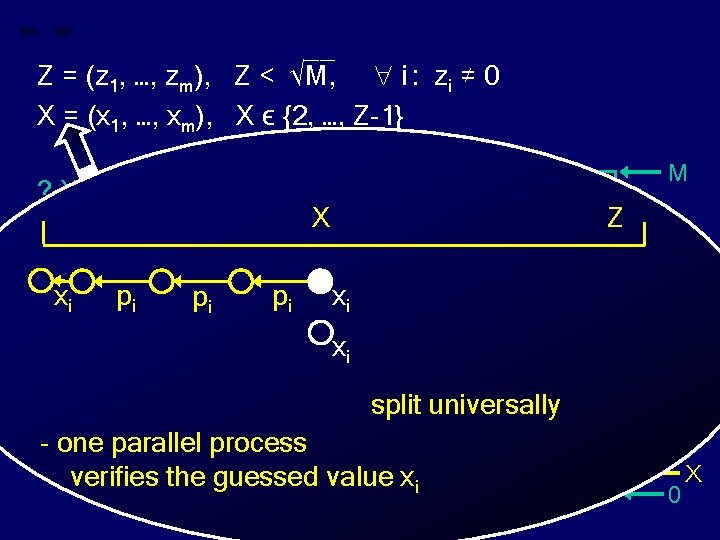
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} M ? X divides Z ? xi pi pi X pi Z xi xi split universally - one parallel process verifies the guessed value xi Z 0 X

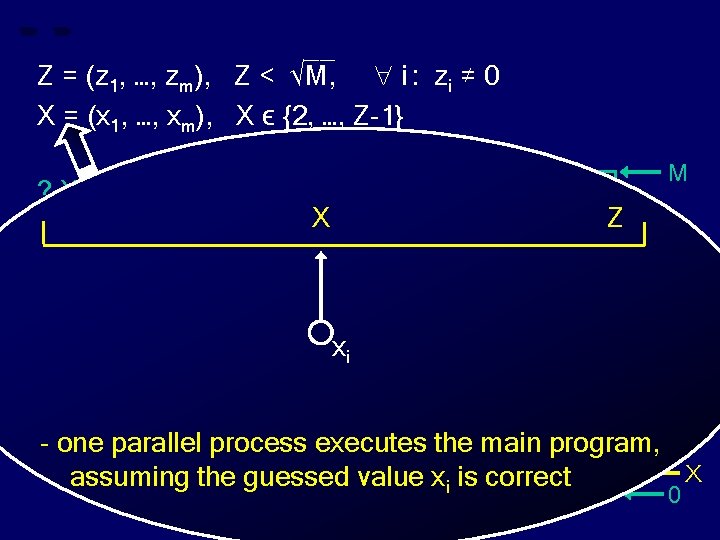
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} ? X divides Z ? M X Z xi - one parallel process executes the main program, Z X assuming the guessed value xi is correct 0

__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} ? X divides Z ? M X Z zi required, for some i Z 0 X

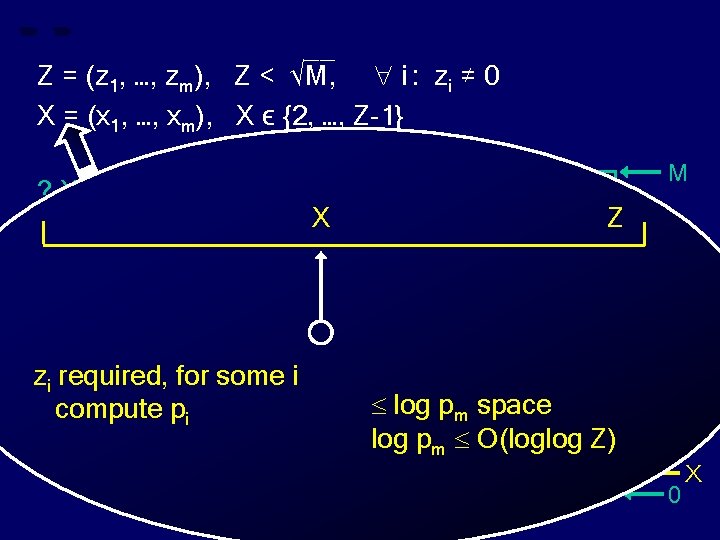
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} ? X divides Z ? zi required, for some i compute pi M X Z log pm space log pm O(loglog Z) Z 0 X

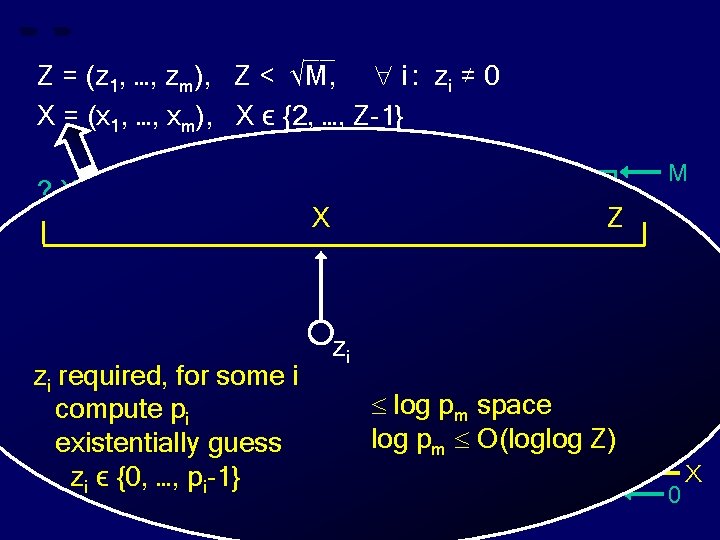
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} ? X divides Z ? zi required, for some i compute pi existentially guess zi ϵ {0, …, pi-1} M X Z zi log pm space log pm O(loglog Z) Z 0 X

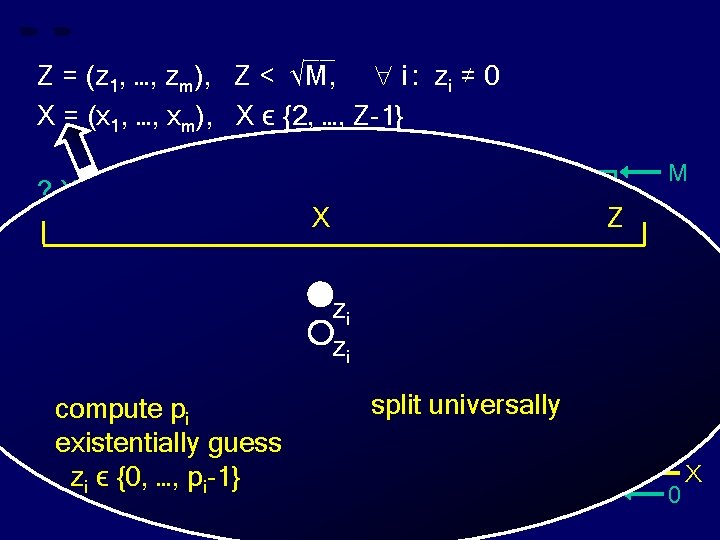
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} ? X divides Z ? M X Z zi zi compute pi existentially guess zi ϵ {0, …, pi-1} split universally Z 0 X

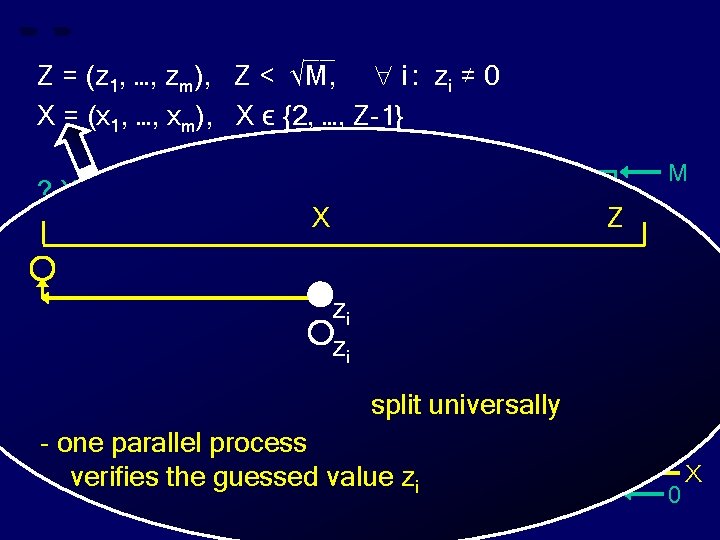
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} ? X divides Z ? M X Z zi zi split universally - one parallel process verifies the guessed value zi Z 0 X

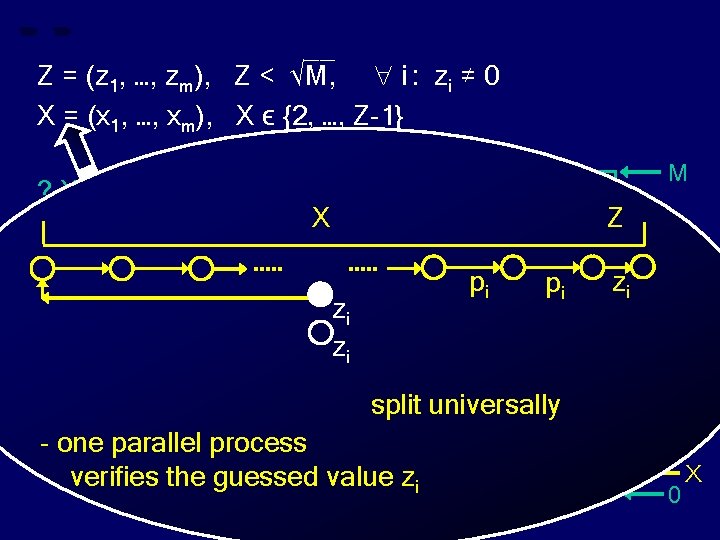
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} ? X divides Z ? M X Z pi zi zi pi zi split universally - one parallel process verifies the guessed value zi Z 0 X

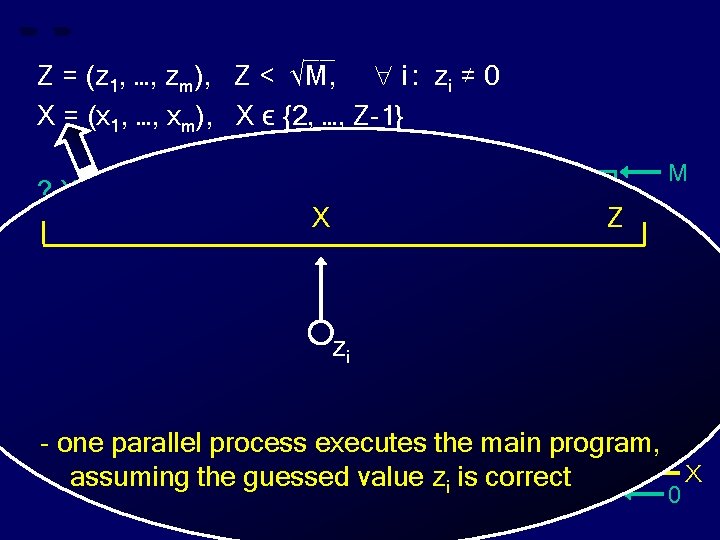
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} ? X divides Z ? M X Z zi - one parallel process executes the main program, Z X assuming the guessed value zi is correct 0

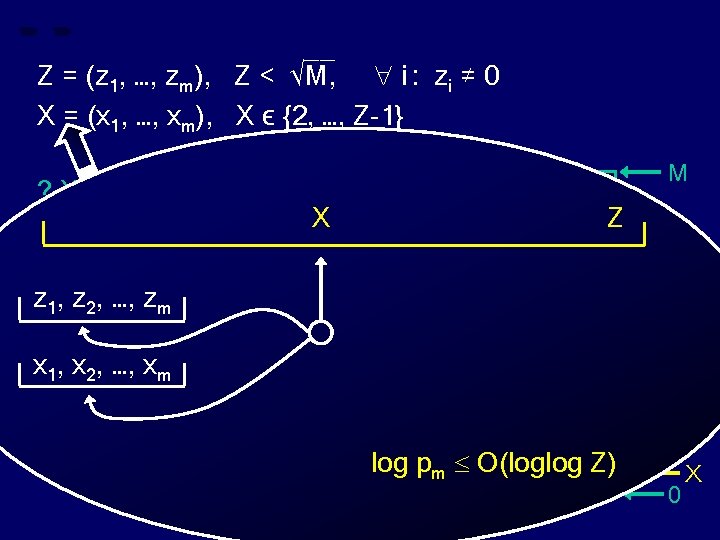
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} ? X divides Z ? M X Z z 1, z 2, …, zm x 1, x 2, …, xm log pm O(loglog Z) Z 0 X

__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} ? X divides Z ? M if xi = 0 then “X does not divide Z” Z 0 X

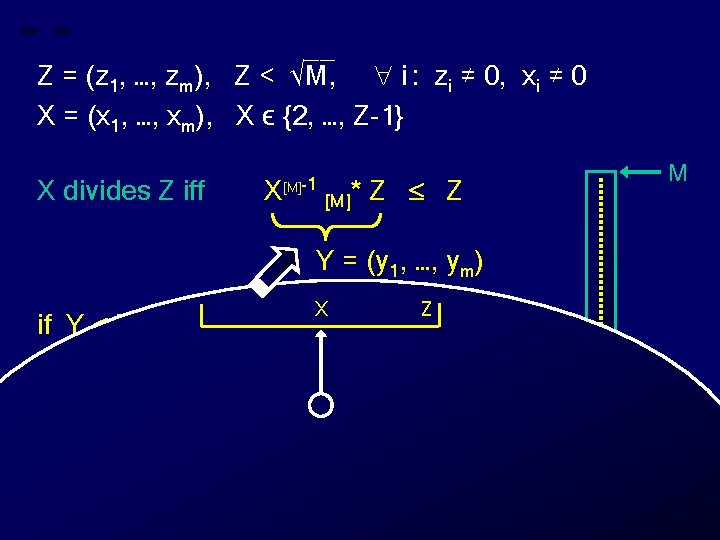
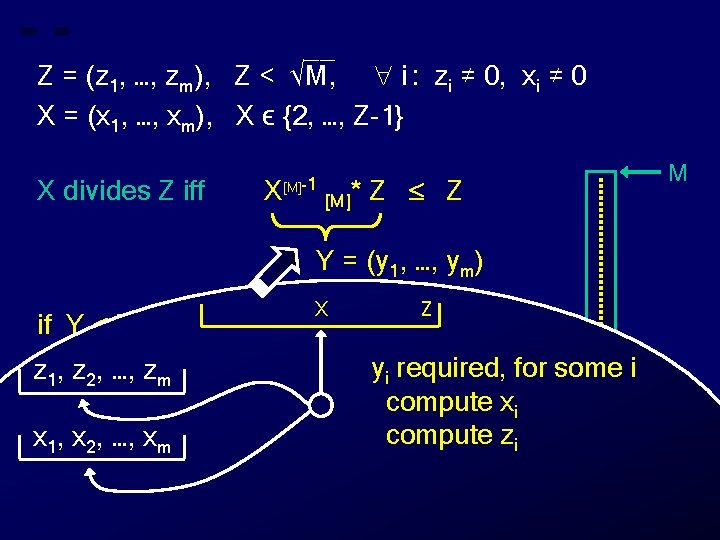
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0, xi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} X divides Z iff X [M]-1 [M]* Z Z M Z 0 X

__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0, xi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} X divides Z iff X [M]-1 [M]* Z Z M M = p 1. p 2. …. pm Z 0 X

__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0, xi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} X divides Z iff X [M]-1 [M]* Z Z M M = p 1. p 2. …. pm X [M]* Y = (X * Y) mod M = (x 1 [p 1]* y 1, …, xm [pm]* ym) Z 0 X

__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0, xi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} X divides Z iff X [M]-1 [M]* Z Z M M = p 1. p 2. …. pm X [M]* Y = (X * Y) mod M = (x 1 [p 1]* y 1, …, xm X[M]-1 : X[M]-1 [pm]* ym) Z X [M]* X[M]-1 = (x 1[p 1]-1, …, xm[pm]-1), i: xi ≠ 0 0 X

__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0, xi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} X divides Z iff X [M]-1 [M]* Z Z M Z 0 X

__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0, xi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} X divides Z iff X [M]-1 [M]* Z Z M Y = (y 1, …, ym) Z 0 Y X

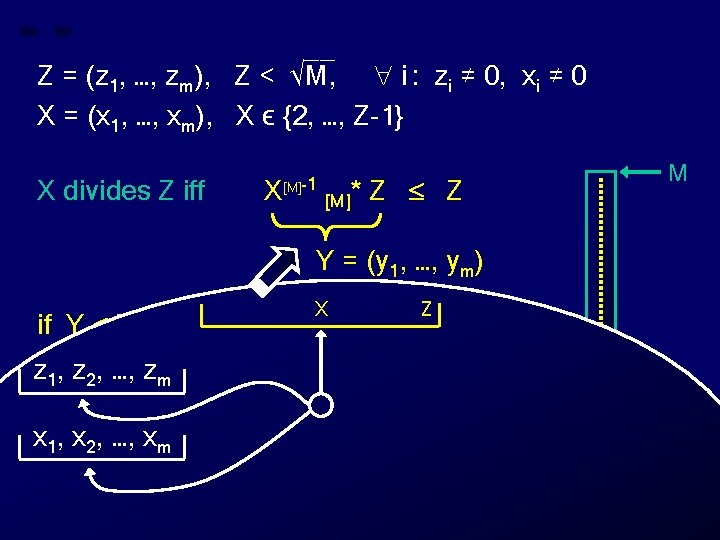
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0, xi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} X divides Z iff X [M]-1 [M]* Z Z M Y = (y 1, …, ym) if Y Z then “X divides Z” else “X does not divide Z” Z 0 Y X

__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0, xi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} X divides Z iff X [M]-1 [M]* Z Z M Y = (y 1, …, ym) X Z if Y Z then “X divides Z” else “X does not divide Z” Z 0 Y X

__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0, xi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} X divides Z iff X [M]-1 [M]* Z Z M Y = (y 1, …, ym) X Z if Y Z then “X divides Z” z , …, zelse “X does not divide Z” 1 2 m Z x 1, x 2, …, xm 0 Y X

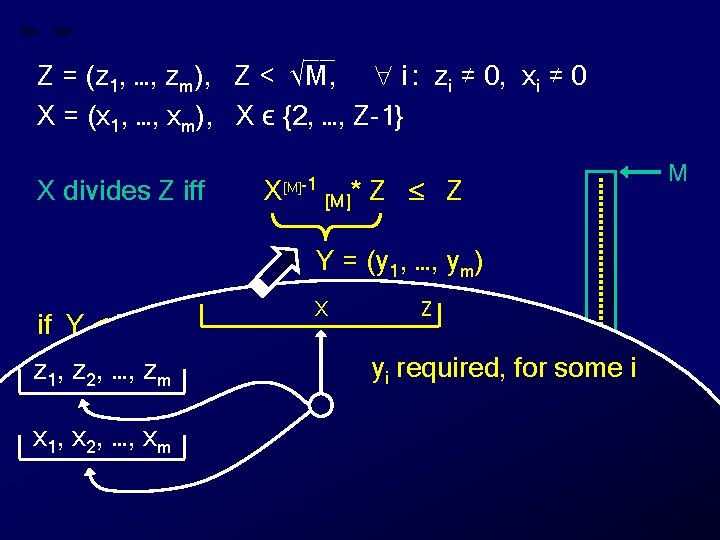
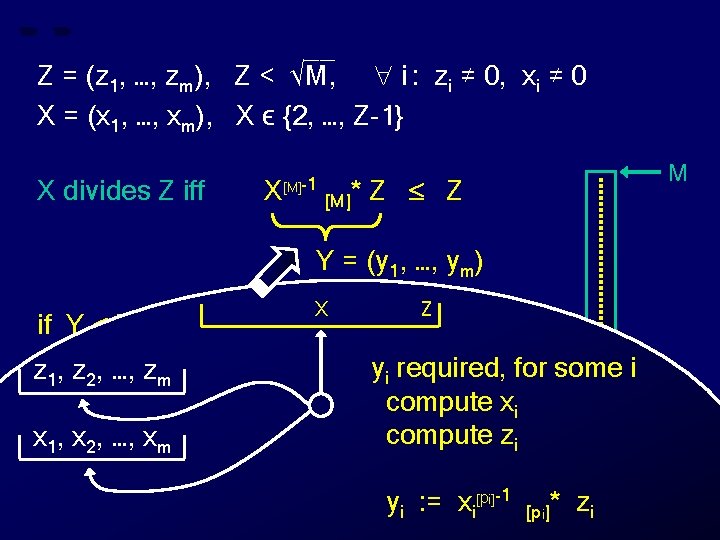
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0, xi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} X divides Z iff X [M]-1 [M]* Z Z M Y = (y 1, …, ym) X Z if Y Z then “X divides Z” Z” for some i y required, z , …, zelse “X does not divide 1 2 m i Z x 1, x 2, …, xm 0 Y X

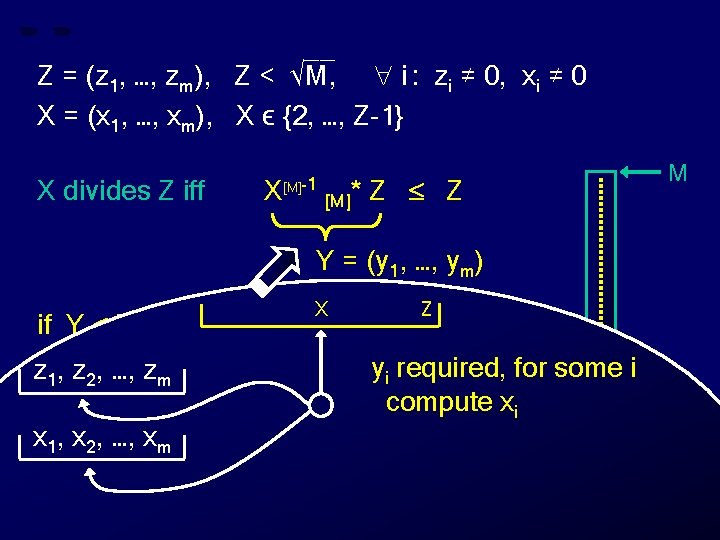
__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0, xi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} X divides Z iff X [M]-1 [M]* Z Z M Y = (y 1, …, ym) X Z if Y Z then “X divides Z” Z” for some i y required, z , …, zelse “X does not divide 1 2 m x 1, x 2, …, xm i compute xi Z 0 Y X

__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0, xi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} X divides Z iff X [M]-1 [M]* Z Z M Y = (y 1, …, ym) X Z if Y Z then “X divides Z” Z” for some i y required, z , …, zelse “X does not divide 1 2 m x 1, x 2, …, xm i compute xi compute zi Z 0 Y X

__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0, xi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} X divides Z iff X [M]-1 [M]* M Z Z Y = (y 1, …, ym) X Z if Y Z then “X divides Z” Z” for some i y required, z , …, zelse “X does not divide 1 2 m x 1, x 2, …, xm i compute xi compute zi yi : = xi[pi]-1 Z [pi]* zi 0 Y X

__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0, xi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} X divides Z iff X [M]-1 [M]* Z Z M Y = (y 1, …, ym) if Y Z then “X divides Z” else “X does not divide Z” Z 0 Y X

__ Z = (z 1, …, zm), Z < √M, i : zi ≠ 0, xi ≠ 0 X = (x 1, …, xm), X ϵ {2, …, Z-1} X divides Z iff X [M]-1 [M]* Z Z M Y = (y 1, …, ym) - to solve the problem we only need an algorithm deciding whether Y Z - for any given Y Z 0 Y X

__ Z = (z 1, …, zm), 0 Z < √M Y = (y 1, …, ym), 0 Y < M ? Y Z ? M Thm: Let Z = (z 1, …, zm) and Y = (y 1, …, ym) be two numbers in the residual representation, Z M/2. Z 0 Y

__ Z = (z 1, …, zm), 0 Z < √M Y = (y 1, …, ym), 0 Y < M ? Y Z ? M Thm: Let Z = (z 1, …, zm) and Y = (y 1, …, ym) be two numbers in the residual representation, Z M/2. If the values zi and yi can effectively be computed in O(log pm) space, for each given i {1, …, m}, Z 0 Y

__ Z = (z 1, …, zm), 0 Z < √M Y = (y 1, …, ym), 0 Y < M ? Y Z ? Thm: Let Z = (z 1, …, zm) and Y = (y 1, …, ym) be two numbers in the residual representation, Z M/2. If the values zi and yi can effectively be computed in O(log pm) space, for each given i {1, …, m}, then the question of whether Y Z can also be decided in O(log pm) space. M Z 0 Y

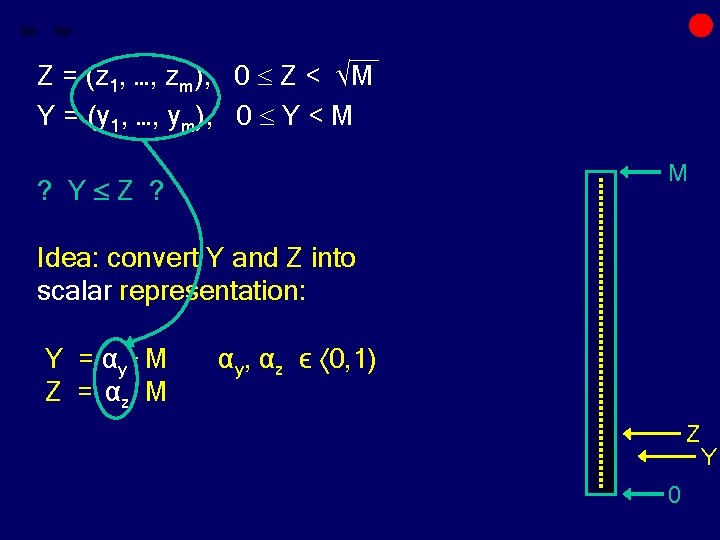
__ Z = (z 1, …, zm), 0 Z < √M Y = (y 1, …, ym), 0 Y < M ? Y Z ? M Idea: convert Y and Z into scalar representation: Z 0 Y

__ Z = (z 1, …, zm), 0 Z < √M Y = (y 1, …, ym), 0 Y < M M ? Y Z ? Idea: convert Y and Z into scalar representation: Y = αy. M Z = αz. M αy, αz ϵ 0, 1) Z 0 Y

__ Z = (z 1, …, zm), 0 Z < √M Y = (y 1, …, ym), 0 Y < M M ? Y Z ? Idea: convert Y and Z into scalar representation: Y = αy. M Z = αz. M αy, αz ϵ 0, 1) Z 0 Y

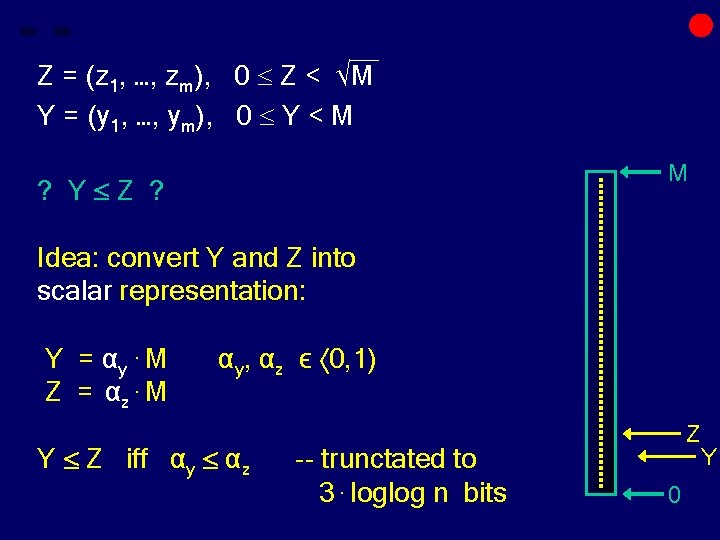
__ Z = (z 1, …, zm), 0 Z < √M Y = (y 1, …, ym), 0 Y < M M ? Y Z ? Idea: convert Y and Z into scalar representation: Y = αy. M Z = αz. M αy, αz ϵ 0, 1) Z Y Z iff αy αz 0 Y

__ Z = (z 1, …, zm), 0 Z < √M Y = (y 1, …, ym), 0 Y < M M ? Y Z ? Idea: convert Y and Z into scalar representation: Y = αy. M Z = αz. M αy, αz ϵ 0, 1) Y Z iff αy αz -- trunctated to 3. loglog n bits Z 0 Y

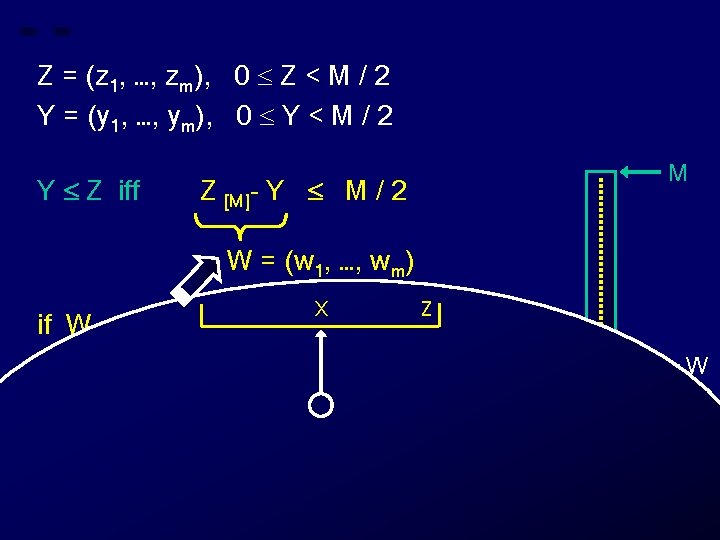
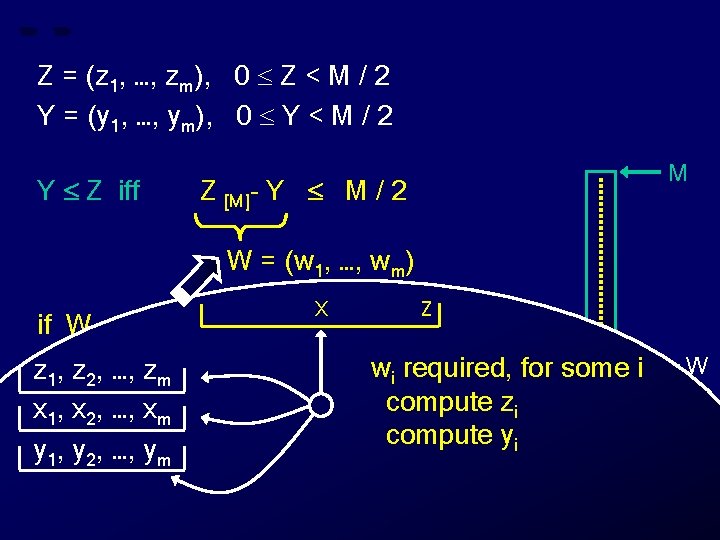
Z = (z 1, …, zm), 0 Z < M / 2 Y = (y 1, …, ym), 0 Y < M / 2 Y Z iff Z [M]- Y M / 2 M Z 0 Y

Z = (z 1, …, zm), 0 Z < M / 2 Y = (y 1, …, ym), 0 Y < M / 2 Y Z iff Z [M]- Y M / 2 M W = (w 1, …, wm) W Z 0 Y

Z = (z 1, …, zm), 0 Z < M / 2 Y = (y 1, …, ym), 0 Y < M / 2 Y Z iff Z [M]- Y M / 2 M W = (w 1, …, wm) if W M / 2 then “Y Z” else “Y > Z” W Z 0 Y

Z = (z 1, …, zm), 0 Z < M / 2 Y = (y 1, …, ym), 0 Y < M / 2 Y Z iff M Z [M]- Y M / 2 W = (w 1, …, wm) X if W M / 2 then “Y Z” else “Y > Z” Z W Z 0 Y

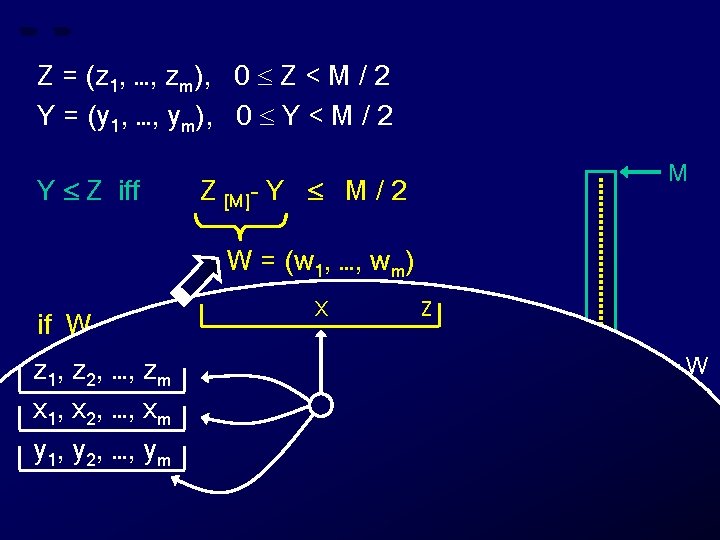
Z = (z 1, …, zm), 0 Z < M / 2 Y = (y 1, …, ym), 0 Y < M / 2 Y Z iff M Z [M]- Y M / 2 W = (w 1, …, wm) X if W M / 2 then “Y Z” else “Y > Z” z , …, z 1 2 Z W m x 1, x 2, …, xm y 1, y 2, …, ym Z 0 Y

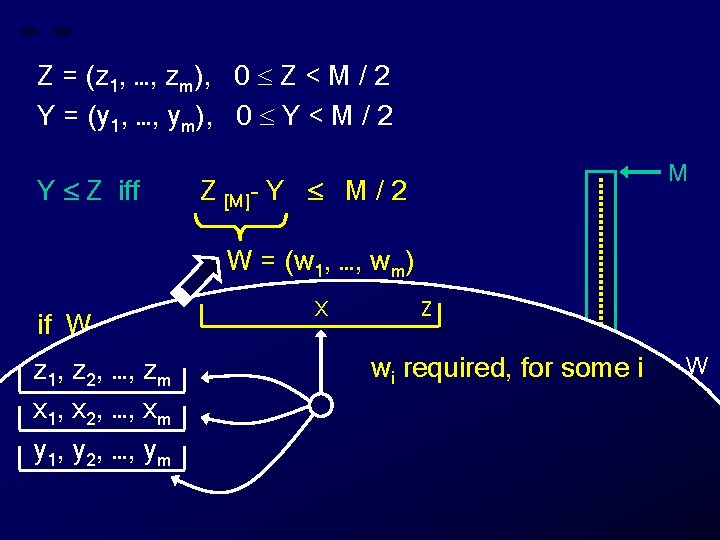
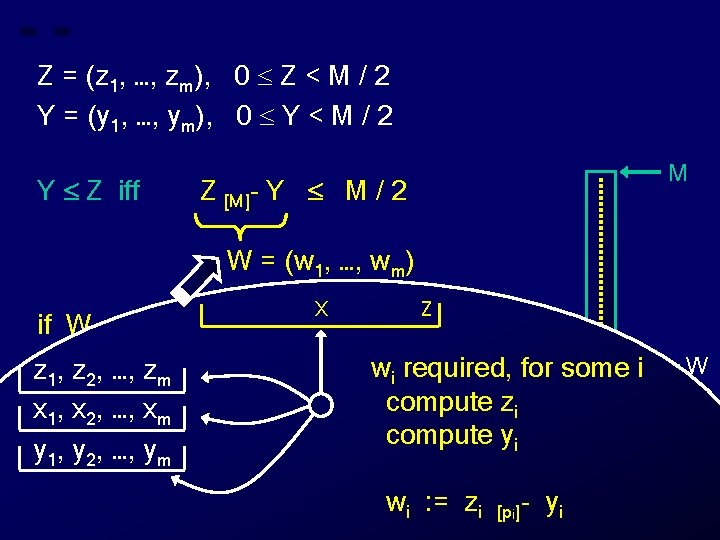
Z = (z 1, …, zm), 0 Z < M / 2 Y = (y 1, …, ym), 0 Y < M / 2 Y Z iff M Z [M]- Y M / 2 W = (w 1, …, wm) X Z if W M / 2 then “Y Z” z 1, z 2, …, zm else “Y > Z” wi required, for some i x 1, x 2, …, xm y 1, y 2, …, ym W Z 0 Y

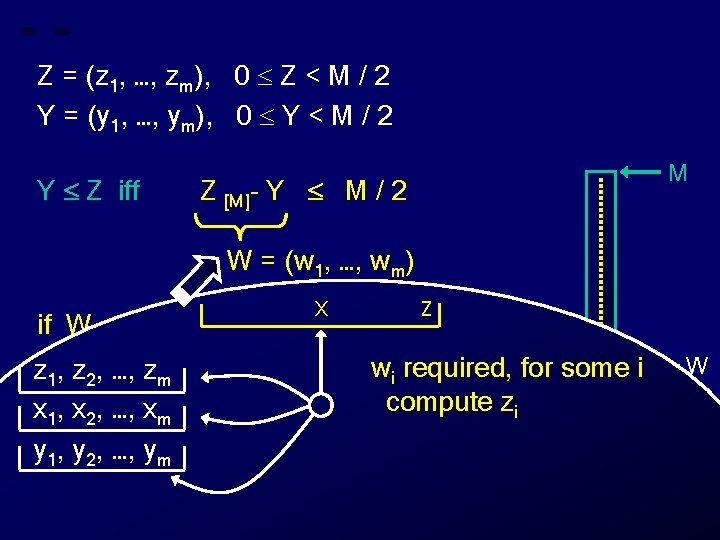
Z = (z 1, …, zm), 0 Z < M / 2 Y = (y 1, …, ym), 0 Y < M / 2 Y Z iff M Z [M]- Y M / 2 W = (w 1, …, wm) X Z if W M / 2 then “Y Z” z 1, z 2, …, zm else “Y > Z” wi required, for some i compute zi x 1, x 2, …, xm y 1, y 2, …, ym W Z 0 Y

Z = (z 1, …, zm), 0 Z < M / 2 Y = (y 1, …, ym), 0 Y < M / 2 Y Z iff M Z [M]- Y M / 2 W = (w 1, …, wm) X Z if W M / 2 then “Y Z” z 1, z 2, …, zm else “Y > Z” wi required, for some i compute zi x 1, x 2, …, xm compute yi y 1, y 2, …, ym W Z 0 Y

Z = (z 1, …, zm), 0 Z < M / 2 Y = (y 1, …, ym), 0 Y < M / 2 Y Z iff M Z [M]- Y M / 2 W = (w 1, …, wm) X Z if W M / 2 then “Y Z” z 1, z 2, …, zm else “Y > Z” wi required, for some i compute zi x 1, x 2, …, xm compute yi y 1, y 2, …, ym wi : = zi [pi]- yi W Z 0 Y

Z = (z 1, …, zm), 0 Z < M / 2 Y = (y 1, …, ym), 0 Y < M / 2 Y Z iff Z [M]- Y M / 2 M W = (w 1, …, wm) if W M / 2 then “Y Z” else “Y > Z” W Z 0 Y

Z = (z 1, …, zm), 0 Z < M / 2 Y = (y 1, …, ym), 0 Y < M / 2 Y Z iff Z [M]- Y M / 2 M W = (w 1, …, wm) - to decide whether Y Z, we only need an algorithm deciding whether W M/2 W - for any given W Z 0 Y

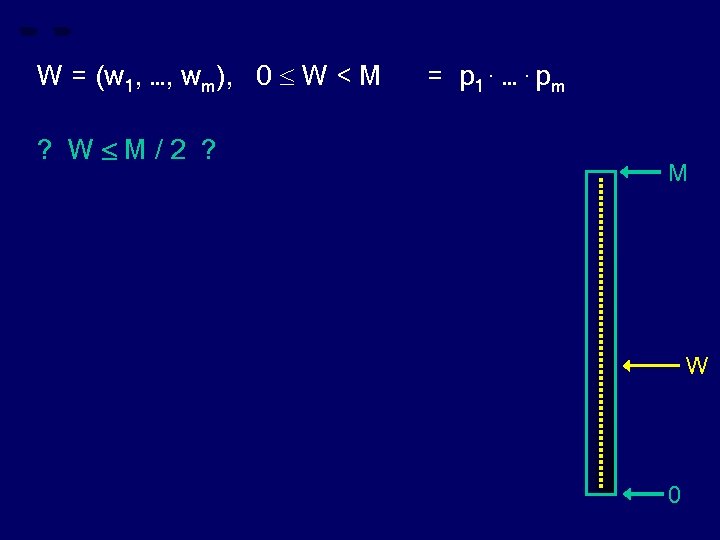
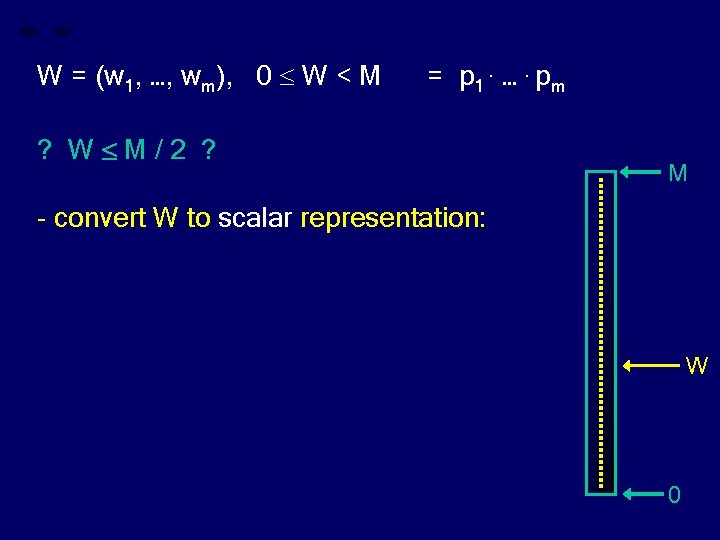
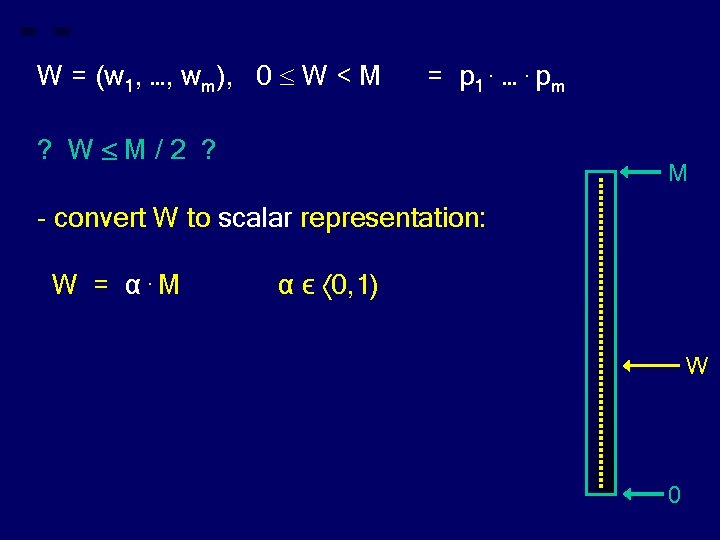
W = (w 1, …, wm), 0 W < M = p 1. …. pm ? W M/2 ? M - convert W to scalar representation: W 0

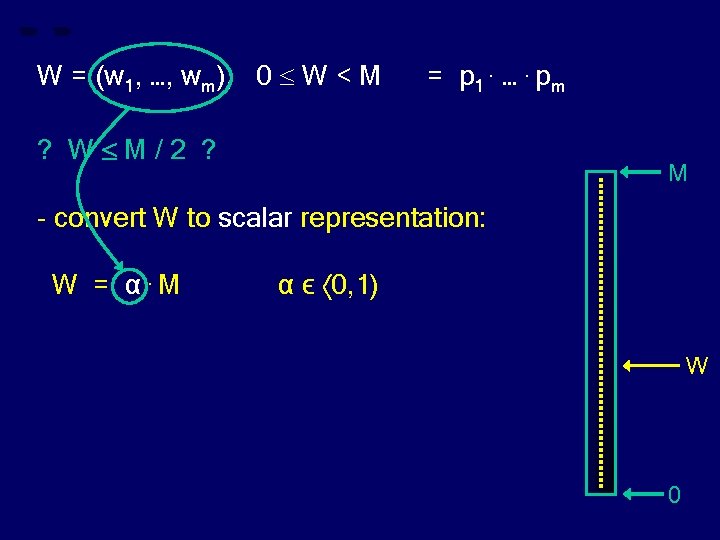
W = (w 1, …, wm), 0 W < M = p 1. …. pm ? W M/2 ? M - convert W to scalar representation: W = α. M α ϵ 0, 1) W 0

W = (w 1, …, wm), 0 W < M = p 1. …. pm ? W M/2 ? M - convert W to scalar representation: W = α. M α ϵ 0, 1) W 0

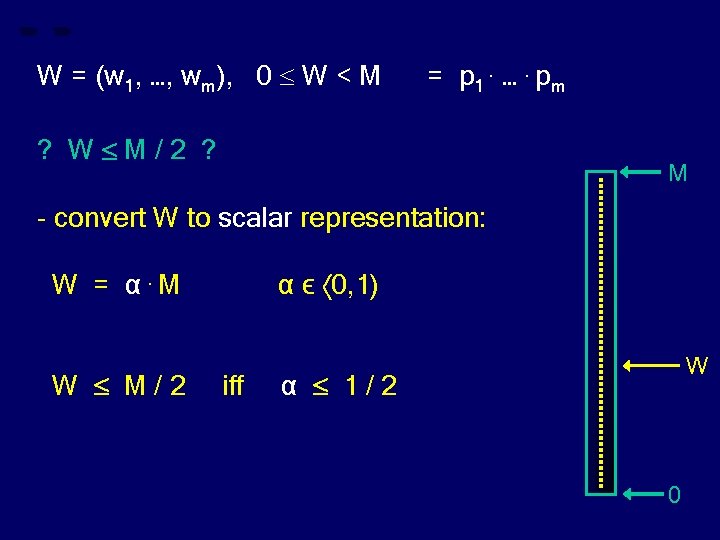
W = (w 1, …, wm), 0 W < M = p 1. …. pm ? W M/2 ? M - convert W to scalar representation: α ϵ 0, 1) W = α. M W M/2 iff W α 1/2 0

W = (w 1, …, wm), 0 W < M α= m m [1]Σ ([pi]Π i=1 j=1, j i = p 1. …. pm pj )[pi]-1 [pi]. wi / pi 1 / 2 ?

W = (w 1, …, wm), 0 W < M α= m m [1]Σ ([pi]Π i=1 j=1, j i = p 1. …. pm pj )[pi]-1 [pi]. wi / pi 1 / 2 ? α : = 0. 00 for i : = 1, …, m do c : = 1 for j : = 1, …, m do if j ≠ i then c : = c [pi]. pj end c : = c[pi]-1 ; c : = c [pi]. wi φ : = c / pi α : = α [1]+ φ end

W = (w 1, …, wm), 0 W < M α= m m [1]Σ ([pi]Π i=1 j=1, j i = p 1. …. pm pj )[pi]-1 [pi]. wi / pi 1 / 2 ? integer arithmetic modulo pi α : = 0. 00 for i : = 1, …, m do c : = 1 for j : = 1, …, m do if j ≠ i then c : = c [pi]. pj end c : = c[pi]-1 ; c : = c [pi]. wi φ : = c / pi α : = α [1]+ φ end

W = (w 1, …, wm), 0 W < M α= m m [1]Σ ([pi]Π i=1 j=1, j i pj )[pi]-1 [pi]. wi / pi 1 / 2 ? integer arithmetic modulo pi O(log pm) space = p 1. …. pm α : = 0. 00 for i : = 1, …, m do c : = 1 for j : = 1, …, m do if j ≠ i then c : = c [pi]. pj end c : = c[pi]-1 ; c : = c [pi]. wi φ : = c / pi α : = α [1]+ φ end

W = (w 1, …, wm), 0 W < M α= m m [1]Σ ([pi]Π i=1 j=1, j i = p 1. …. pm pj )[pi]-1 [pi]. wi / pi 1 / 2 ? integer arithmetic modulo pi O(log pm) space log pm O(loglog Z) α : = 0. 00 for i : = 1, …, m do c : = 1 for j : = 1, …, m do if j ≠ i then c : = c [pi]. pj end c : = c[pi]-1 ; c : = c [pi]. wi φ : = c / pi α : = α [1]+ φ end

W = (w 1, …, wm), 0 W < M α= m m [1]Σ ([pi]Π i=1 j=1, j i real arithmetic = p 1. …. pm pj )[pi]-1 [pi]. wi / pi 1 / 2 ? α : = 0. 00 for i : = 1, …, m do c : = 1 for j : = 1, …, m do if j ≠ i then c : = c [pi]. pj end c : = c[pi]-1 ; c : = c [pi]. wi φ : = c / pi α : = α [1]+ φ end

W = (w 1, …, wm), 0 W < M α= m m [1]Σ ([pi]Π i=1 j=1, j i = p 1. …. pm pj )[pi]-1 [pi]. wi / pi 1 / 2 ? real arithmetic O(loglog Z) space α : = 0. 00 for i : = 1, …, m do c : = 1 for j : = 1, …, m do if j ≠ i then c : = c [pi]. pj end c : = c[pi]-1 ; c : = c [pi]. wi φ : = c / pi α : = α [1]+ φ end

W = (w 1, …, wm), 0 W < M α= m m [1]Σ ([pi]Π i=1 j=1, j i = p 1. …. pm pj )[pi]-1 [pi]. wi / pi 1 / 2 ? real arithmetic O(loglog Z) space truncated to ℓ 3. loglog(Z) bits α : = 0. 00 for i : = 1, …, m do c : = 1 for j : = 1, …, m do if j ≠ i then c : = c [pi]. pj end c : = c[pi]-1 ; c : = c [pi]. wi φ : = c / pi α : = α [1]+ φ end

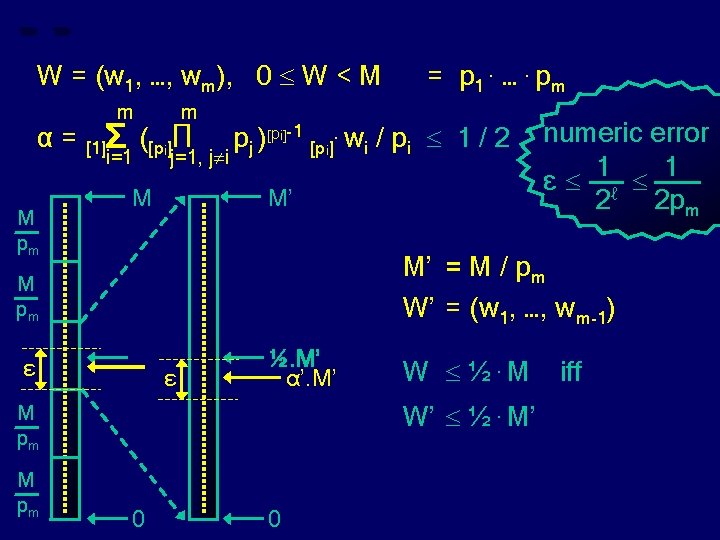
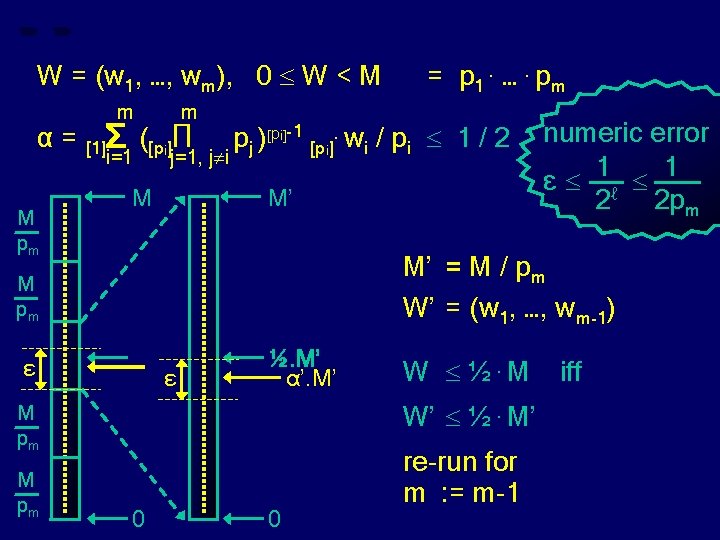
W = (w 1, …, wm), 0 W < M α= m = p 1. …. pm m pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error j=1, j i 1 1 ε ℓ 2 2 pm α : = 0. 00 [1]Σ ([pi]Π i=1 real arithmetic O(loglog Z) space truncated to ℓ 3. loglog(Z) bits for i : = 1, …, m do c : = 1 for j : = 1, …, m do if j ≠ i then c : = c [pi]. pj end c : = c[pi]-1 ; c : = c [pi]. wi φ : = c / pi α : = α [1]+ φ end

W = (w 1, …, wm), 0 W < M α= m m = p 1. …. pm pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M 2 2 pm [1]Σ ([pi]Π ½. M 0

W = (w 1, …, wm), 0 W < M α= m m = p 1. …. pm pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M 2 2 pm [1]Σ ([pi]Π α. M ε ½. M 0

W = (w 1, …, wm), 0 W < M α= m m = p 1. …. pm pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M 2 2 pm [1]Σ ([pi]Π α. M ε ½. M 0

W = (w 1, …, wm), 0 W < M α= m m = p 1. …. pm pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M 2 2 pm [1]Σ ([pi]Π ½. M α. M ε 0

W = (w 1, …, wm), 0 W < M α= ε m m = p 1. …. pm pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M 2 2 pm [1]Σ ([pi]Π ½. M α. M 0

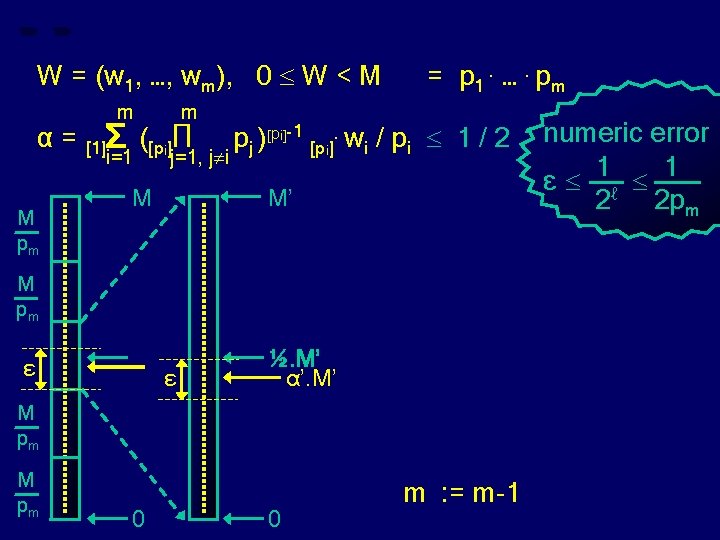
W = (w 1, …, wm), 0 W < M α= M pm m m pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M M’ 2 2 pm [1]Σ ([pi]Π M’ = M / pm W’ = (w 1, …, wm-1) M pm ε ε ½. M’ α’. M’ W ½. M W’ ½. M’ M pm = p 1. …. pm 0 0 iff

W = (w 1, …, wm), 0 W < M α= M pm m m pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M M’ 2 2 pm [1]Σ ([pi]Π M’ = M / pm W’ = (w 1, …, wm-1) M pm ε ε ½. M’ α’. M’ W ½. M W’ ½. M’ M pm = p 1. …. pm 0 0 re-run for m : = m-1 iff

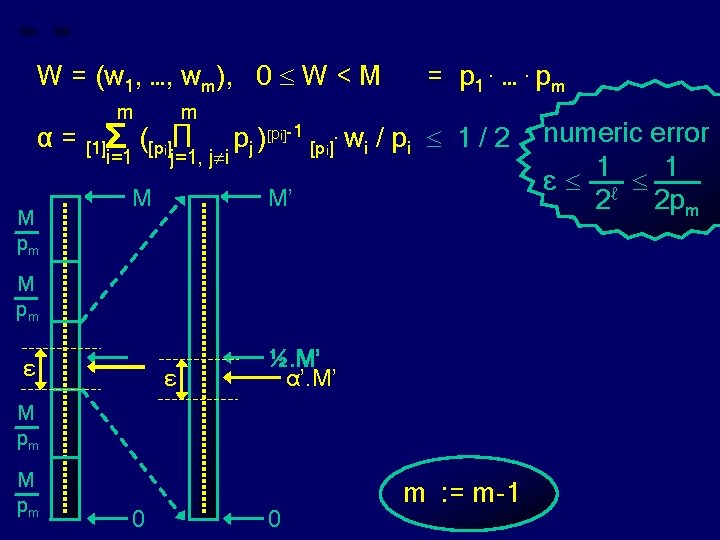
W = (w 1, …, wm), 0 W < M α= M pm m = p 1. …. pm m pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M M’ 2 2 pm [1]Σ ([pi]Π M pm ε ε ½. M’ α’. M’ M pm 0 0 m : = m-1

W = (w 1, …, wm), 0 W < M α= M pm m = p 1. …. pm m pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M M’ 2 2 pm [1]Σ ([pi]Π M pm ε ε ½. M’ α’. M’ M pm 0 0 m : = m-1

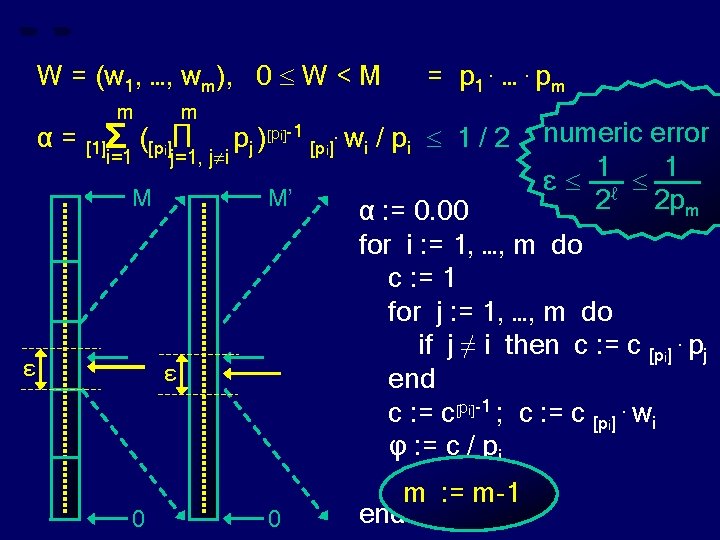
W = (w 1, …, wm), 0 W < M α= M pm m m pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M M’ 2 2 pm α : = 0. 00 [1]Σ ([pi]Π M pm ε ε M pm = p 1. …. pm 0 for i : = 1, …, m do c : = 1 for j : = 1, …, m do. p if j ≠ i then c : = c [pi] j ½. M’ α’. M’ end c : = c[pi]-1 ; c : = c [pi]. wi φ : = c / pi αm: = α [1] +φ m-1 end 0

W = (w 1, …, wm), 0 W < M α= M pm m m pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M M’ 2 2 pm α : = 0. 00 [1]Σ ([pi]Π M pm ε ε M pm = p 1. …. pm 0 for i : = 1, …, m do c : = 1 for j : = 1, …, m do. p if j ≠ i then c : = c [pi] j ½. M’ α’. M’ end c : = c[pi]-1 ; c : = c [pi]. wi φ : = c / pi αm: = α [1] +φ m-1 end 0

W = (w 1, …, wm), 0 W < M α= m = p 1. …. pm m pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M M’ 2 2 pm α : = 0. 00 [1]Σ ([pi]Π ε ε 0 for i : = 1, …, m do c : = 1 for j : = 1, …, m do. p if j ≠ i then c : = c [pi] j ½. M’ α’. M’ end c : = c[pi]-1 ; c : = c [pi]. wi φ : = c / pi α : = α [1]+ φ end 0

W = (w 1, …, wm), 0 W < M α= m = p 1. …. pm m pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M M’ 2 2 pm α : = 0. 00 [1]Σ ([pi]Π ε ε 0 for i : = 1, …, m do c : = 1 for j : = 1, …, m do. p if j ≠ i then c : = c [pi] j ½. M’ end c : = c[pi]-1 ; c : = c [pi]. wi α’. M’ φ : = c / pi α : = α [1]+ φ end 0

W = (w 1, …, wm), 0 W < M α= m = p 1. …. pm m pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M M’ 2 2 pm α : = 0. 00 [1]Σ ([pi]Π ε ε 0 for i : = 1, …, m do c : = 1 for j : = 1, …, m do. p if j ≠ i then c : = c [pi] j ½. M’ end α’. M’ c : = c[pi]-1 ; c : = c [pi]. wi φ : = c / pi α : = α [1]+ φ end 0

W = (w 1, …, wm), 0 W < M α= m = p 1. …. pm m pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M M’ 2 2 pm α : = 0. 00 [1]Σ ([pi]Π ε ε 0 for i : = 1, …, m do c : = 1 α’. M’ for j : = 1, …, m do. p if j ≠ i then c : = c [pi] j ½. M’ end c : = c[pi]-1 ; c : = c [pi]. wi φ : = c / pi α : = α [1]+ φ end 0

W = (w 1, …, wm), 0 W < M α= m = p 1. …. pm m pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M M’ 2 2 pm α : = 0. 00 [1]Σ ([pi]Π ε ε 0 for i : = 1, …, m do c : = 1 for j : = 1, …, m do. p if j ≠ i then c : = c [pi] j ½. M’ α’. M’ end c : = c[pi]-1 ; c : = c [pi]. wi φ : = c / pi α : = α [1]+ φ end 0

W = (w 1, …, wm), 0 W < M α= m = p 1. …. pm m pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M M’ 2 2 pm α : = 0. 00 [1]Σ ([pi]Π ε ε 0 0 for i : = 1, …, m do c : = 1 for j : = 1, …, m do if j ≠ i then c : = c [pi]. pj end c : = c[pi]-1 ; c : = c [pi]. wi φ : = c / pi α : = α [1]+ φ end

W = (w 1, …, wm), 0 W < M α= m = p 1. …. pm m pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M M’ 2 2 pm α : = 0. 00 [1]Σ ([pi]Π ε ε 0 0 for i : = 1, …, m do c : = 1 for j : = 1, …, m do if j ≠ i then c : = c [pi]. pj end c : = c[pi]-1 ; c : = c [pi]. wi φ : = c / pi αm: = α [1] +φ m-1 end

W = (w 1, …, wm), 0 W < M α= m = p 1. …. pm m pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M M’ 2 2 pm α : = 0. 00 [1]Σ ([pi]Π ε ε 0 0 for i : = 1, …, m do c : = 1 for j : = 1, …, m do if j ≠ i then c : = c [pi]. pj end c : = c[pi]-1 ; c : = c [pi]. wi φ : = c / pi αm: = α [1] +φ m-1 end

W = (w 1, …, wm), 0 W < M α= m = p 1. …. pm m pj )[pi]-1 [pi]. wi / pi 1 / 2 ? numeric error i=1 j=1, j i 1 1 ε ℓ M M’ 2 2 pm α : = 0. 00 [1]Σ ([pi]Π ε ε 0 0 for i : = 1, …, m do c : = 1 for… jrepeated : = 1, …, m do. p if j ≠ i then c : = c until the question [pi] j end W p -1 M / 2 c : = c[ i] ; c : = c [pi]. wi is solved φ : = c / pi αm: = α [1] +φ m-1 end

un-Primes, un-Composites ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n)

un-Primes, un-Composites ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n) ϵ accept-ASPACE x REVERSALS(loglog n)

un-Primes, un-Composites ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n) ϵ accept-ASPACE x REVERSALS(loglog n) --optimal, cannot be improved

un-Primes, un-Composites ϵ accept-ASPACE(loglog n) ϵ pebble-DSPACE(loglog n) ϵ accept-ASPACE x REVERSALS(loglog n) --optimal, cannot be improved below loglog n, only regular languages accepted (even with the help of alternation)

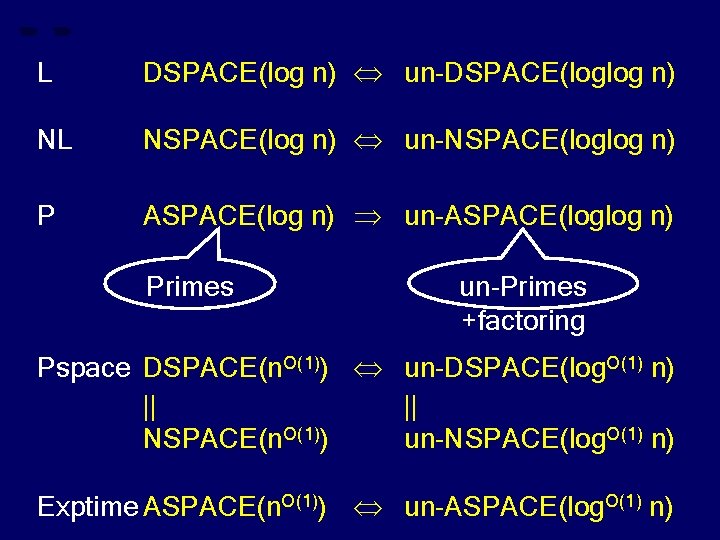
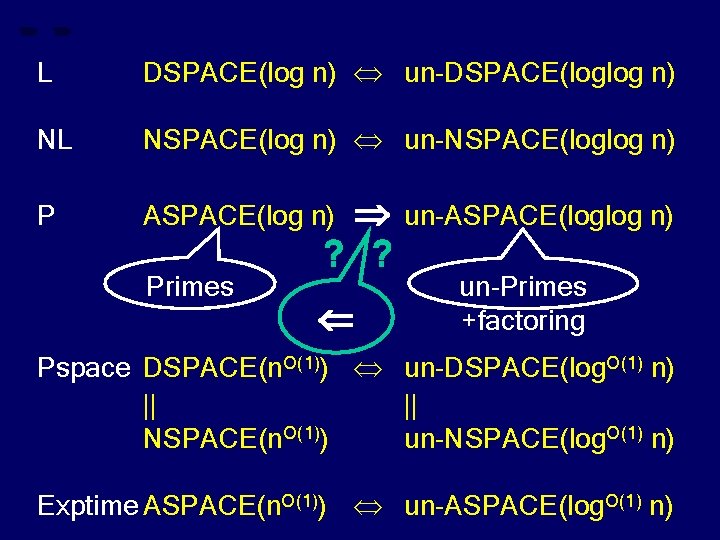
L DSPACE(log n) un-DSPACE(loglog n) NL NSPACE(log n) un-NSPACE(loglog n) P ASPACE(log n) un-ASPACE(loglog n) Pspace DSPACE(n. O(1)) un-DSPACE(log. O(1) n) || || NSPACE(n. O(1)) un-NSPACE(log. O(1) n) Exptime ASPACE(n. O(1)) un-ASPACE(log. O(1) n)

L DSPACE(log n) un-DSPACE(loglog n) NL NSPACE(log n) un-NSPACE(loglog n) P ASPACE(log n) un-ASPACE(loglog n) Primes Pspace DSPACE(n. O(1)) un-DSPACE(log. O(1) n) || || NSPACE(n. O(1)) un-NSPACE(log. O(1) n) Exptime ASPACE(n. O(1)) un-ASPACE(log. O(1) n)

L DSPACE(log n) un-DSPACE(loglog n) NL NSPACE(log n) un-NSPACE(loglog n) P ASPACE(log n) un-ASPACE(loglog n) Primes un-Primes Pspace DSPACE(n. O(1)) un-DSPACE(log. O(1) n) || || NSPACE(n. O(1)) un-NSPACE(log. O(1) n) Exptime ASPACE(n. O(1)) un-ASPACE(log. O(1) n)

L DSPACE(log n) un-DSPACE(loglog n) NL NSPACE(log n) un-NSPACE(loglog n) P ASPACE(log n) un-ASPACE(loglog n) Primes un-Primes +factoring Pspace DSPACE(n. O(1)) un-DSPACE(log. O(1) n) || || NSPACE(n. O(1)) un-NSPACE(log. O(1) n) Exptime ASPACE(n. O(1)) un-ASPACE(log. O(1) n)

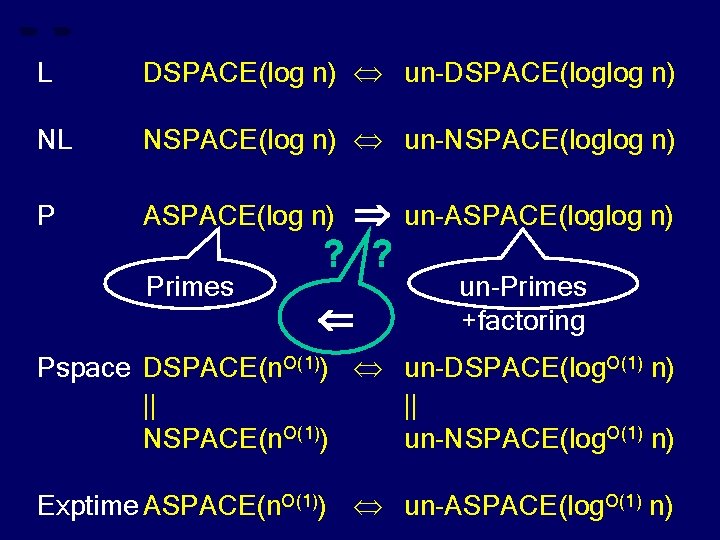
L DSPACE(log n) un-DSPACE(loglog n) NL NSPACE(log n) un-NSPACE(loglog n) P ASPACE(log n) Primes ? ? un-ASPACE(loglog n) un-Primes +factoring Pspace DSPACE(n. O(1)) un-DSPACE(log. O(1) n) || || NSPACE(n. O(1)) un-NSPACE(log. O(1) n) Exptime ASPACE(n. O(1)) un-ASPACE(log. O(1) n)

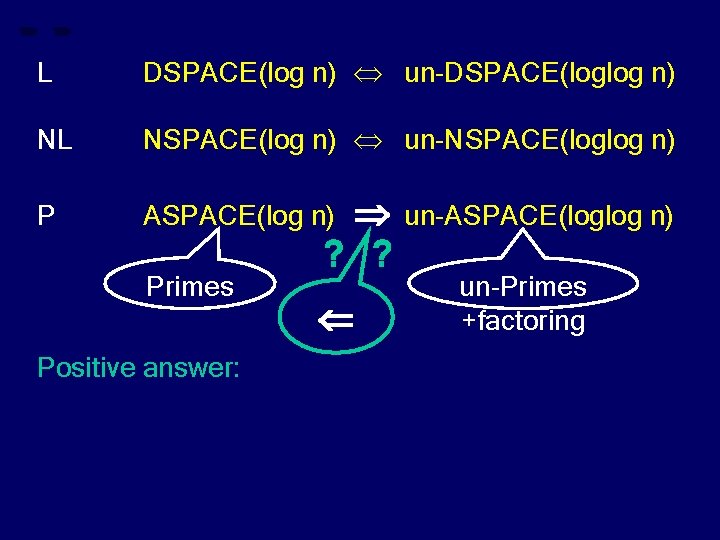
L DSPACE(log n) un-DSPACE(loglog n) NL NSPACE(log n) un-NSPACE(loglog n) P ASPACE(log n) Primes Positive answer: ? ? un-ASPACE(loglog n) un-Primes +factoring

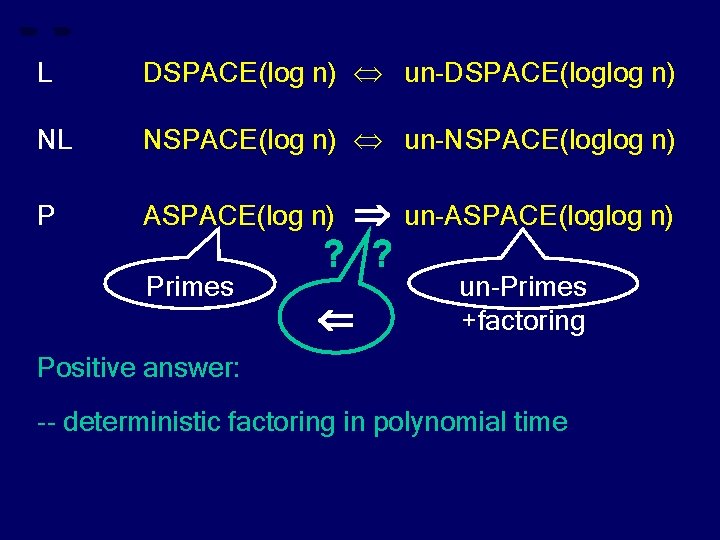
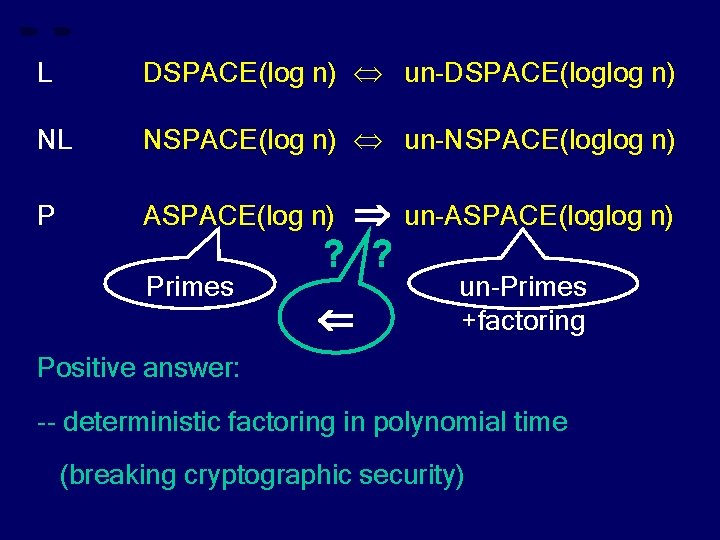
L DSPACE(log n) un-DSPACE(loglog n) NL NSPACE(log n) un-NSPACE(loglog n) P ASPACE(log n) Primes ? ? un-ASPACE(loglog n) un-Primes +factoring Positive answer: -- deterministic factoring in polynomial time

L DSPACE(log n) un-DSPACE(loglog n) NL NSPACE(log n) un-NSPACE(loglog n) P ASPACE(log n) Primes ? ? un-ASPACE(loglog n) un-Primes +factoring Positive answer: -- deterministic factoring in polynomial time (breaking cryptographic security)

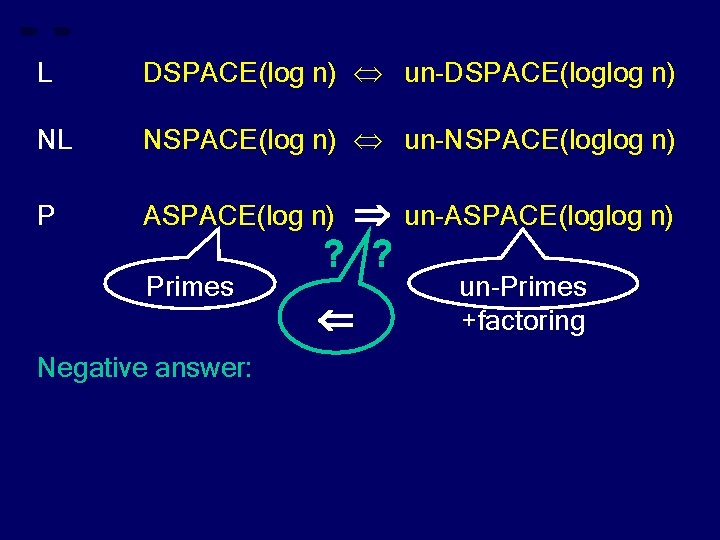
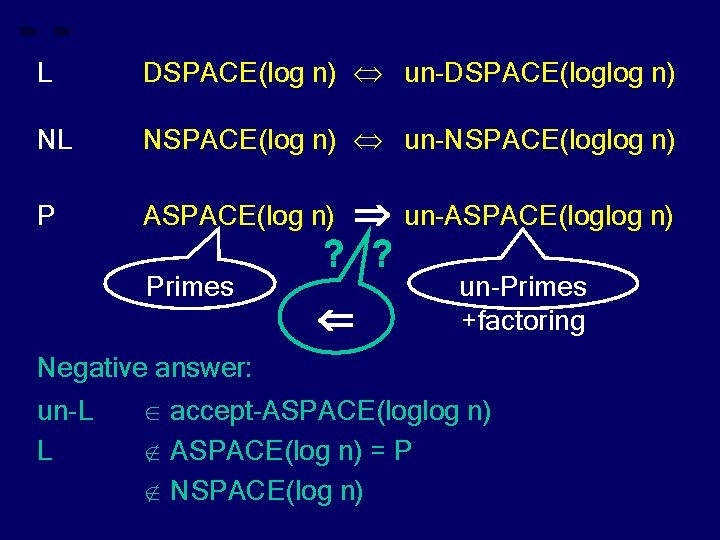
L DSPACE(log n) un-DSPACE(loglog n) NL NSPACE(log n) un-NSPACE(loglog n) P ASPACE(log n) Primes Negative answer: ? ? un-ASPACE(loglog n) un-Primes +factoring

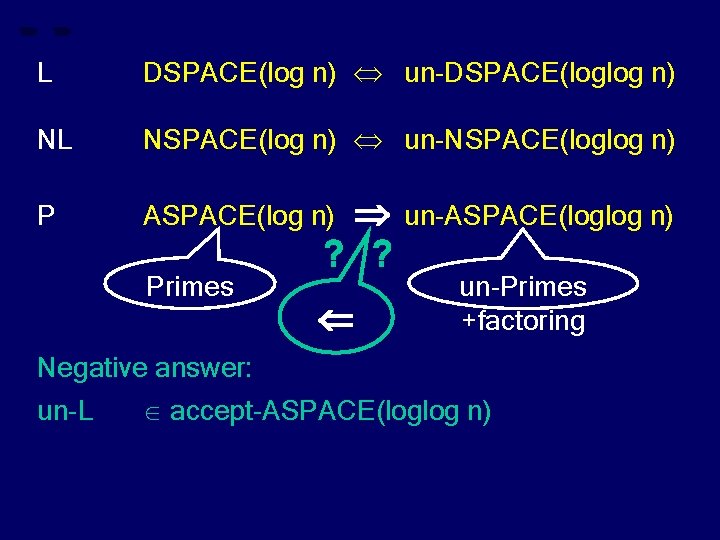
L DSPACE(log n) un-DSPACE(loglog n) NL NSPACE(log n) un-NSPACE(loglog n) P ASPACE(log n) Primes ? ? un-ASPACE(loglog n) un-Primes +factoring Negative answer: un-L accept-ASPACE(loglog n)

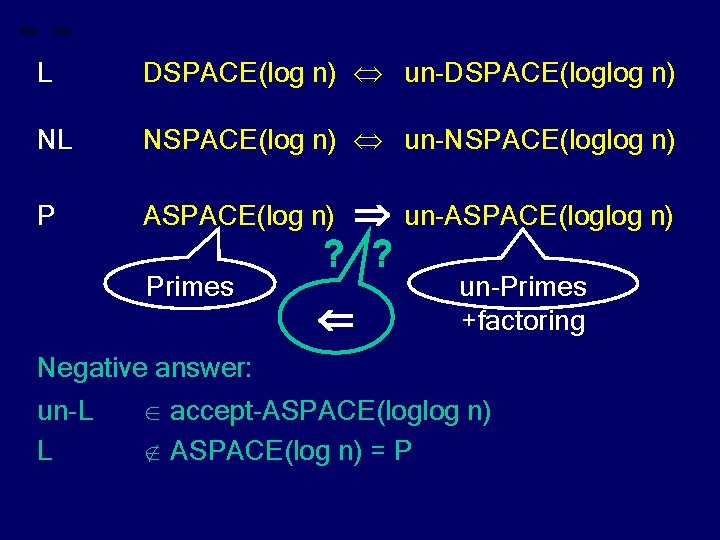
L DSPACE(log n) un-DSPACE(loglog n) NL NSPACE(log n) un-NSPACE(loglog n) P ASPACE(log n) Primes ? ? un-ASPACE(loglog n) un-Primes +factoring Negative answer: un-L L accept-ASPACE(loglog n) ASPACE(log n) = P

L DSPACE(log n) un-DSPACE(loglog n) NL NSPACE(log n) un-NSPACE(loglog n) P ASPACE(log n) Primes ? ? un-ASPACE(loglog n) un-Primes +factoring Negative answer: un-L L accept-ASPACE(loglog n) ASPACE(log n) = P NSPACE(log n)

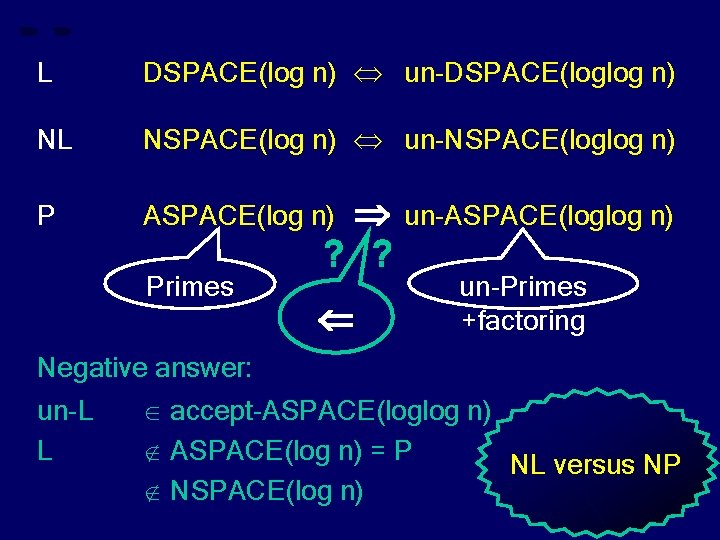
L DSPACE(log n) un-DSPACE(loglog n) NL NSPACE(log n) un-NSPACE(loglog n) P ASPACE(log n) Primes ? ? un-ASPACE(loglog n) un-Primes +factoring Negative answer: un-L L accept-ASPACE(loglog n) ASPACE(log n) = P NL versus NP NSPACE(log n)

L DSPACE(log n) un-DSPACE(loglog n) NL NSPACE(log n) un-NSPACE(loglog n) P ASPACE(log n) Primes ? ? un-ASPACE(loglog n) un-Primes +factoring Pspace DSPACE(n. O(1)) un-DSPACE(log. O(1) n) || || NSPACE(n. O(1)) un-NSPACE(log. O(1) n) Exptime ASPACE(n. O(1)) un-ASPACE(log. O(1) n)

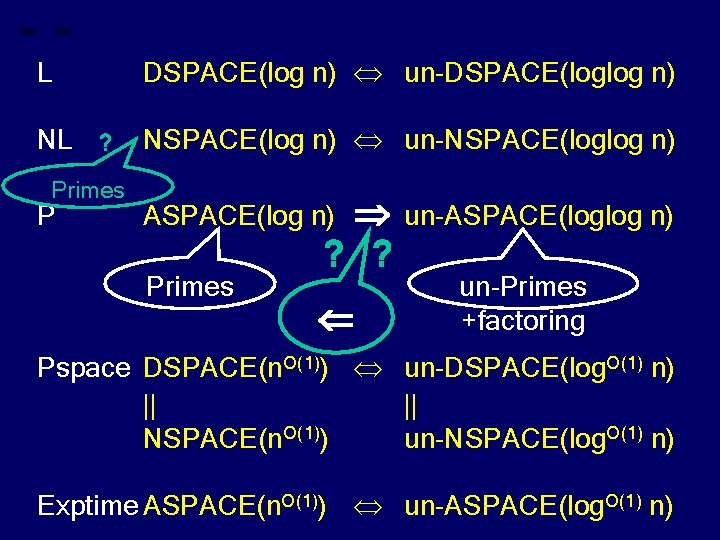
L DSPACE(log n) un-DSPACE(loglog n) NL ? NSPACE(log n) un-NSPACE(loglog n) Primes P ? ? ASPACE(log n) Primes un-ASPACE(loglog n) un-Primes +factoring Pspace DSPACE(n. O(1)) un-DSPACE(log. O(1) n) || || NSPACE(n. O(1)) un-NSPACE(log. O(1) n) Exptime ASPACE(n. O(1)) un-ASPACE(log. O(1) n)

Thank You for Your Attention

Thank You for Your Attention

Thank You for Your Attention