Factoring Using Distributive Property and Grouping Using Distributive

Factoring Using Distributive Property and Grouping

Using Distributive Property 1) Find the GCF 2) Write GCF on outside of parenthesis 3) Write remaining factors inside parenthesis

Exs of Distributive Prop 1) 12 a + 16 a 2) 18 cd + 12 c d + 9 cd

Factoring by Grouping 1) Group terms with common factors 2) Factor GCF from each group 3) Rewrite as the product of polynomials

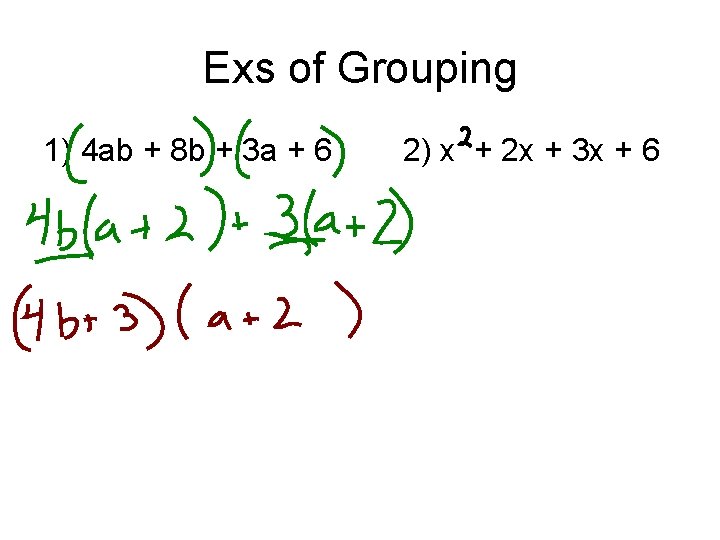
Exs of Grouping 1) 4 ab + 8 b + 3 a + 6 2) x + 2 x + 3 x + 6

Using the Additive Inverse Property • Factor by grouping and look for common terms, if no common terms are left see if the terms are additive inverses 1) 35 x – 5 xy + 3 y – 21

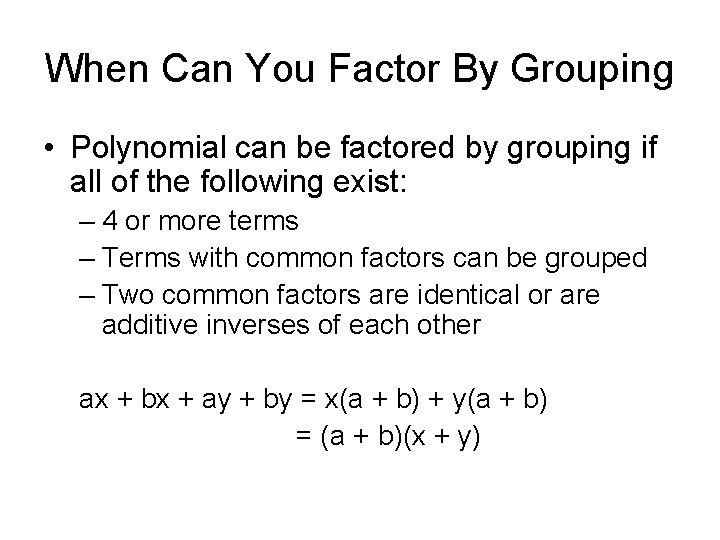
When Can You Factor By Grouping • Polynomial can be factored by grouping if all of the following exist: – 4 or more terms – Terms with common factors can be grouped – Two common factors are identical or are additive inverses of each other ax + bx + ay + by = x(a + b) + y(a + b) = (a + b)(x + y)

Zero Product Property • If the product of 2 factors is 0, then at least one of the factors must be 0. • If ab = 0, then either a = 0, b = 0, or both a and b = 0

Solve an Equation in Factored Form 1) (d – 5)(3 d + 4) = 0 • • Either d – 5 = 0 or 3 d + 4 = 0 Set each factor equal to zero and solve to find your solution set

Solve an Equation by Factoring • If an equation can be written in the form ab = 0, then the zero product property can be applied to solve the equation 1) x = 7 x