4 3 Solving Quadratic Equations by Factoring Recall

4. 3 Solving Quadratic Equations by Factoring

Recall multiplying these binomials to get the standard form for the equation of a quadratic function: (x + 3)(x + 5) = + 5 x +3 x +15 The “reverse” of this process is called factoring. Writing a trinomial as a product of two binomials is called factoring. (x + 3)(x + 5)

Factor Since the lead coefficient is 1, we need two numbers that multiply to – 28 and add to – 12. Factors of -28 -1, 28 1, -28 -2, 14 2, -14 -4, 7 4, -7 Sum of Factors -3 Therefore: 27 -27 12 -12 3

Factor the expression: = (x-3)(x+7) Cannot be factored

Factoring a Trinomial when the lead coefficient is not 1. Factor: We need a combination of factors of 3 and 10 that will give a middle term of – 17. Our approach will guess and check. Here are some possible factorizations: This is the factorization we seek.

Special Factoring Patterns you should remember: Pattern Name Difference of Two Squares Perfect Square Trinomial Pattern Example

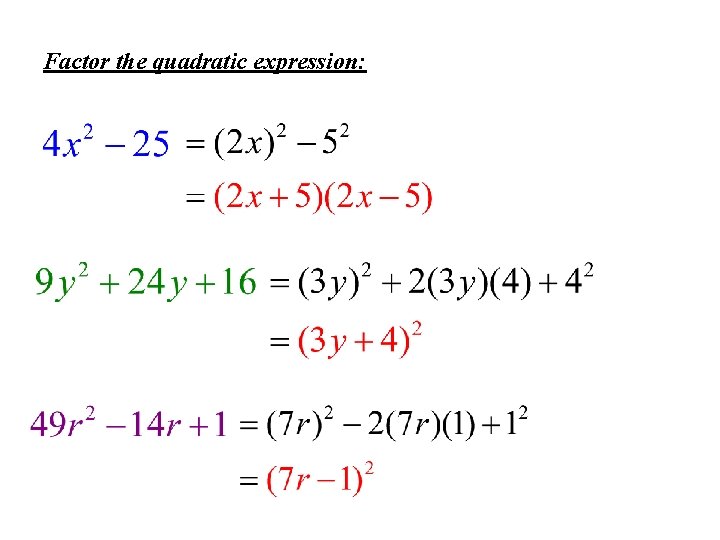
Factor the quadratic expression:

A monomial is an expression that has only one term. As a first step to factoring, you should check to see whether the terms have a common monomial factor. Factor:

You can use factoring to solve certain quadratic equation. A quadratic equation in one variable can be written in the form where This is called the standard form of the equation: If this equation can be factored then we can use this zero product property. Zero Product Property Let A and B be real number or algebraic expressions. If AB = 0 the either A=0 or B=0

Solve: So, either (x+6)=0 Or (x – 3)=0 The solutions are – 6 and 3. These solutions are also called zeros of the function Notice the zeros are the x-intercepts of the graph of the function. x = -6 x=3