Solving Equations by Factoring Definition of Quadratic Equations

Solving Equations by Factoring Definition of Quadratic Equations Zero-Factor Property Strategy for Solving Quadratics

Standard Form Quadratic Equation Quadratic equations can be written in the form ax 2 + bx + c = 0 where a, b, and c are real numbers with a 0. Standard form for a quadratic equation is in descending order equal to zero. BACK

Examples of Quadratic Equations Standard Form BACK

Zero-Factor Property If a and b are real numbers and if ab =0, then a = 0 or b = 0. BACK

Solve the equation (x + 2)(2 x - 1)=0 • By the zero factor property we know. . . • Since the product is equal to zero then one of the factors must be zero. OR BACK

Solve the equation. Check your answers. OR Solution Set BACK

Solve each equation. Check your answers. OR Solution Set BACK

Solving a Quadratic Equation by Factoring Step 1 Write the equation in standard form. Step 2 Factor completely. Step 3 Use the zero-factor property. Set each factor with a variable equal to zero. Step 4 Solve each equation produced in step 3. BACK

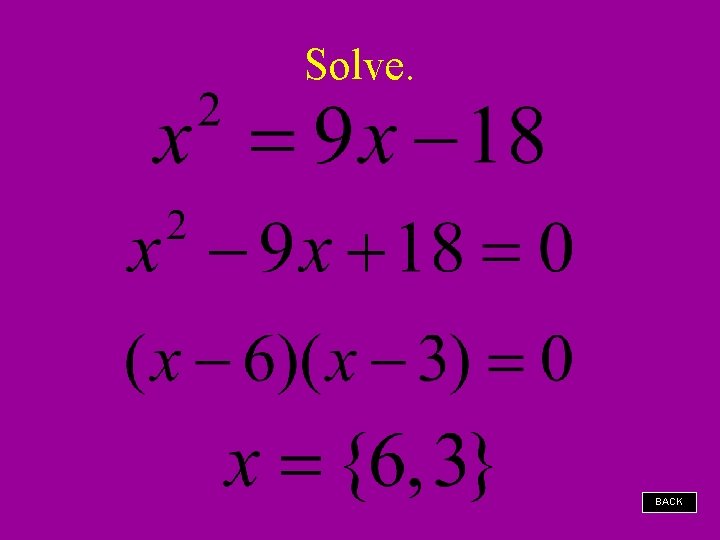
Solve. BACK

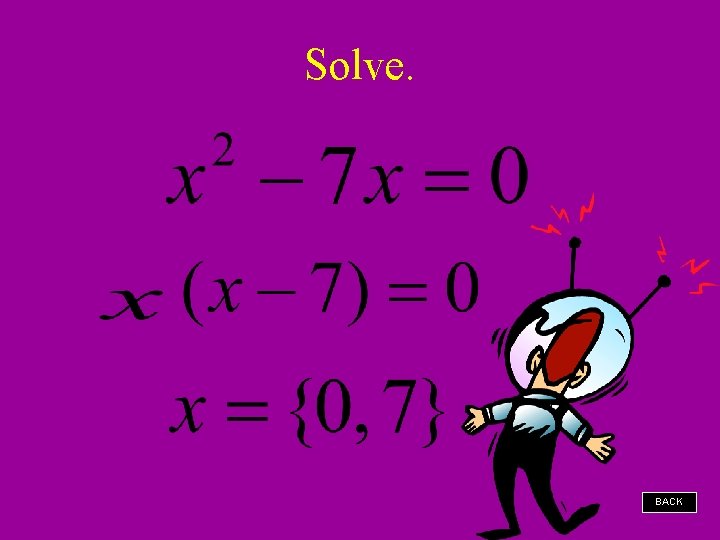
Solve. BACK

Number Of Solutions • The degree of a polynomial is equal to the number of solutions. Three solutions!!!

Example x (x + 1)(x – 3) = 0 Set each of the three factors equal to 0. x=0 x+1=0 x = -1 x– 3=0 x=3 Solve the resulting equations. Write the solution set. x = {0, -1, 3} BACK

Solve the following equations. 1. x 2 – 25 = 0 2. x 2 + 7 x – 8 = 0 3. x 2 – 12 x + 36 = 0 4. c 2 – 8 c = 0

1. Get a value of zero on one side of the equation. 2. Factor the polynomial if possible. 3. Apply the zero product property by setting each factor equal to zero. 4. Solve for the variable.

Solving Equations by Factoring Definition of Quadratic Equations Zero-Factor Property Strategy for Solving Quadratics