Software Testing Techniques STT UNIT6 logic based testing

Software Testing Techniques (STT) UNIT-6 logic based testing Sudhakar yadav Compiled with reference from: Software Testing Techniques: Boris Beizer Craft of Software Testing: Brain Marrick

CONTENTS SYNOPSIS MOTIVATIONAL OVERVIEW DECISION TABLES (HURL 83, VESS 86) PATH EXPRESSIONS AGAIN KV CHARTS SPECIFICATIONS TESTABILITY TIPS

SYNOPSIS Decision tables, which provide a useful basis for program and test design. Consistency and completeness can be analyzed by using boolean algebra, which can also be used as a basis for test design. Boolean algebra is trivialized by using karnaugh-veitch charts.

MOTIVATIONAL OVERVIEW 1. Programmers and Logic “Logic” is one of the most often used words in programmers’ vocabularies but one of their least used techniques.

MOTIVATIONAL OVERVIEW 2. Hardware Logic Testing Hardware logic test design, are intensely automated. Many test methods developed for hardware logic can be adapted to software logic testing. Hardware testing is ahead of software testing not because hardware testers are smarter than software testers but because hardware testing is easier. I say this from the perspective of a former hardware logic designer and tester who has worked in both camps and therefore has a basis for comparison.

MOTIVATIONAL OVERVIEW 3. Specification Systems and Languages (BERZ 85, CHIU 85, HAYE 85, KEMM 85, VESS 86) As programming and test techniques have improved, the bugs have shifted closer to the process front end, to requirements and their specifications. Tools incorporate methods to simplify, transform, and check specifications, and the methods are to a large extent based on boolean algebra.

MOTIVATIONAL OVERVIEW 4. Knowledge-Based Systems The knowledge-based system (also expert system, or “artificial intelligence” system) has become the programming construct of choice for many applications that were once considered very difficult (WATE 86). Knowledge-based systems incorporate knowledge from a knowledge domain such as medicine, law, or civil engineering into a database. The processing is done by a program called the inference engine

MOTIVATIONAL OVERVIEW 5. Overview Programmed tools are nice to have, most of the benefits of boolean algebra can be reaped by wholly manual means if you have the right conceptual tool: the karnaugh -veitch diagram is that conceptual tool.

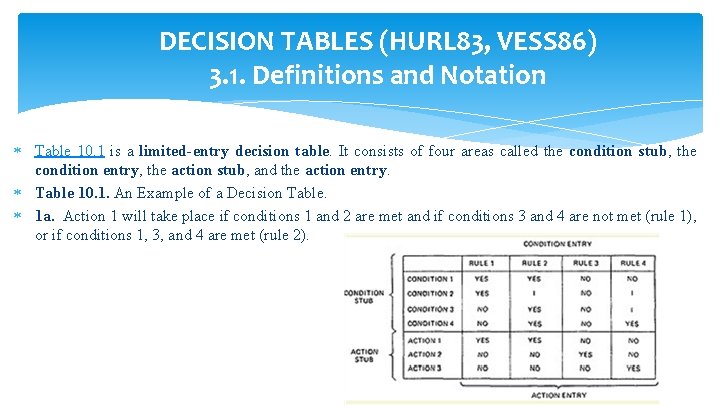
DECISION TABLES (HURL 83, VESS 86) 3. 1. Definitions and Notation Table 10. 1 is a limited-entry decision table. It consists of four areas called the condition stub, the condition entry, the action stub, and the action entry. Table 10. 1. An Example of a Decision Table. 1 a. Action 1 will take place if conditions 1 and 2 are met and if conditions 3 and 4 are not met (rule 1), or if conditions 1, 3, and 4 are met (rule 2).

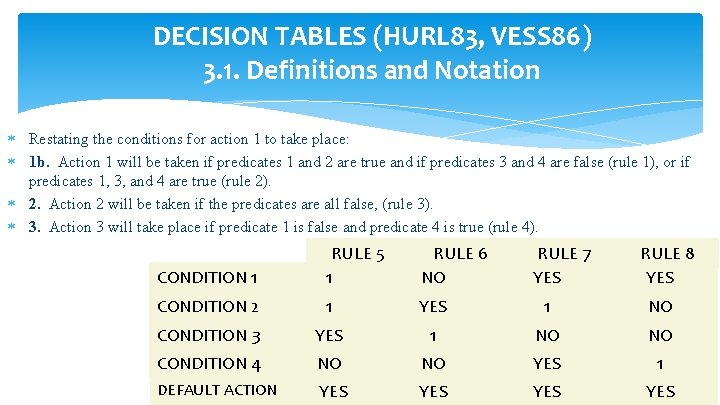
DECISION TABLES (HURL 83, VESS 86) 3. 1. Definitions and Notation Restating the conditions for action 1 to take place: 1 b. Action 1 will be taken if predicates 1 and 2 are true and if predicates 3 and 4 are false (rule 1), or if predicates 1, 3, and 4 are true (rule 2). 2. Action 2 will be taken if the predicates are all false, (rule 3). 3. Action 3 will take place if predicate 1 is false and predicate 4 is true (rule 4). CONDITION 1 RULE 5 1 RULE 6 NO RULE 7 YES RULE 8 YES CONDITION 2 1 YES 1 NO CONDITION 3 YES 1 NO CONDITION 4 NO YES 1 DEFAULT ACTION YES

DECISION TABLES (HURL 83, VESS 86) 2. Decision-Table Processors Decision tables can be automatically translated into code and, as such, are a higher-order language. The decision table’s translator checks the source decision table for consistency and completeness and fills in any required default rules. The usual processing order in the resulting object code is, first, to examine rule 1. If the rule is satisfied, the corresponding action takes place. Otherwise, rule 2 is tried. This process continues until either a satisfied rule results in an action or no rule is satisfied and the default action is taken

DECISION TABLES (HURL 83, VESS 86). 3. Decision Tables as a Basis for Test Case Design The use of a decision-table model to design tests is warranted when: 1. The specification is given as a decision table or can be easily converted into one. 2. The order in which the predicates are evaluated does not affect interpretation of the rules or the resulting action— i. e. , an arbitrary permutation of the predicate order will not, or should not, affect which action takes place. 3. The order in which the rules are evaluated does not affect the resulting action—i. e. , an arbitrary permutation of rules will not, or should not, affect which action takes place. 4. Once a rule is satisfied an action selected, no other rule need be examined. 5. If several actions can result from satisfying a rule, the order in which the actions are executed doesn’t matter.

DECISION TABLES (HURL 83, VESS 86) 4. Expansion of Immaterial Cases Immaterial entries (I) cause most decision-table contradictions. If a condition’s truth value is immaterial in a rule, satisfying the rule does not depend on the condition. It doesn’t mean that the case is impossible. For example, Rule 1: “If the persons are male and over 30, then they shall receive a 15% raise. ” Rule 2: “But if the persons are female, then they shall receive a 10% raise. ”

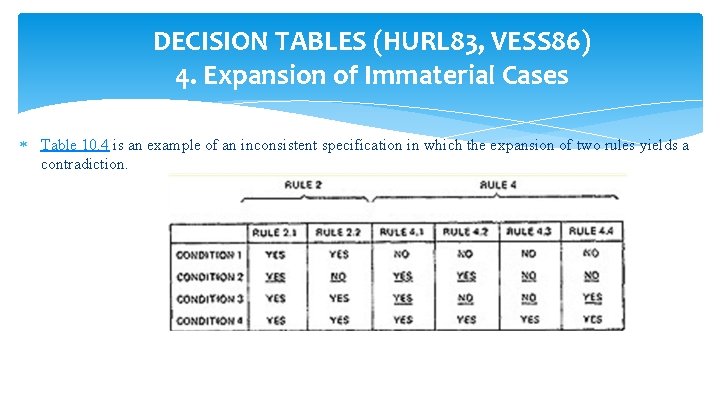
DECISION TABLES (HURL 83, VESS 86) 4. Expansion of Immaterial Cases Table 10. 4 is an example of an inconsistent specification in which the expansion of two rules yields a contradiction.

DECISION TABLES (HURL 83, VESS 86) 3. 5. Test Case Design (GOOD 75, LEWA 76, TAIA 87) If there are k rules over n binary predicates, there at least k cases to consider and at most 2 n cases. It is not usually possible to change the order in which the predicates are evaluated because that order is built into the program, *A tolerant implementation would allow these fields in any order. It is not usually possible to change the order in which the rules are evaluated because that order is built into the program, but if the implementation allows the rule evaluation order to be modified, test different orders for the rules by pairwise interchanges. Identify the places in the routine where rules are invoked or where the processors that evaluate the rules are called. Identify the places where actions are initiated.

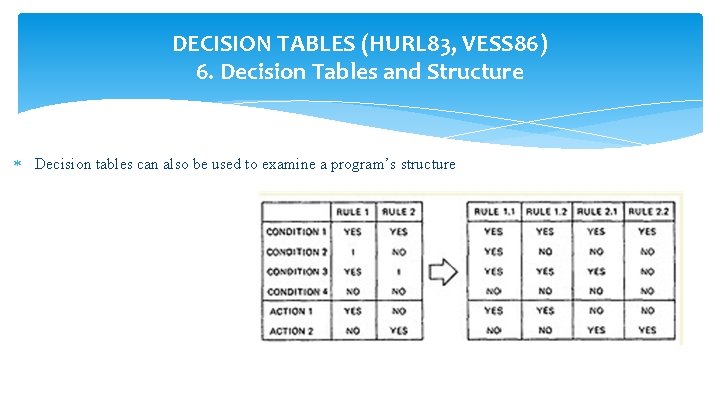
DECISION TABLES (HURL 83, VESS 86) 6. Decision Tables and Structure Decision tables can also be used to examine a program’s structure

DECISION TABLES (HURL 83, VESS 86) 6. Decision Tables and Structure Figure 10. 1. A Sample Program.

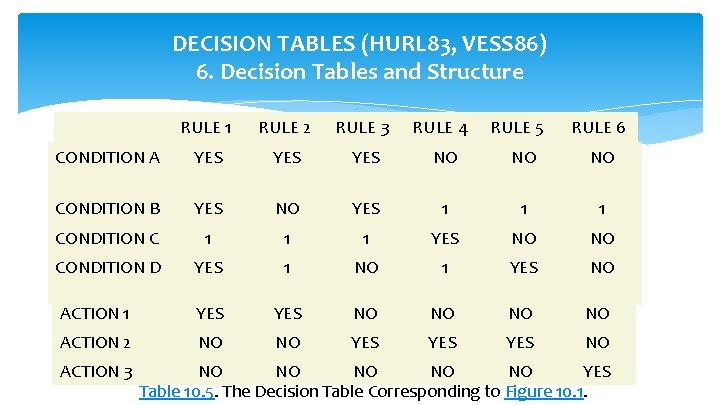
DECISION TABLES (HURL 83, VESS 86) 6. Decision Tables and Structure RULE 1 RULE 2 RULE 3 RULE 4 CONDITION A YES NO NO CONDITION B YES NO YES 1 1 1 CONDITION C 1 1 1 YES NO CONDITION D YES 1 NO 1 YES NO ACTION 1 YES NO NO ACTION 2 NO YES NO ACTION 3 RULE 5 RULE 6 NO NO NO YES Table 10. 5. The Decision Table Corresponding to Figure 10. 1.

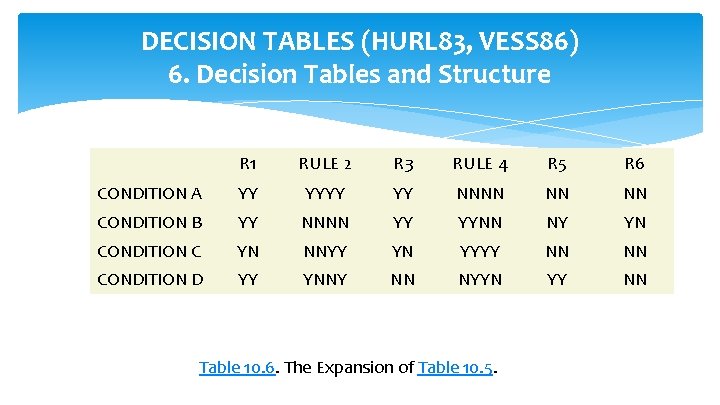
DECISION TABLES (HURL 83, VESS 86) 6. Decision Tables and Structure R 1 RULE 2 R 3 RULE 4 R 5 R 6 CONDITION A YYYY NNNN NN CONDITION B YY NNNN YYNN NY YN CONDITION C YN NNYY YN YYYY NN CONDITION D YY YNNY NN NYYN YY NN Table 10. 6. The Expansion of Table 10. 5.

DECISION TABLES (HURL 83, VESS 86) 6. Decision Tables and Structure Consider the following specification whose putative flowgraph is shown in Figure 10. 2: 1. If condition A is met, do process A 1 no matter what other actions are taken or what other conditions are met. 2. If condition B is met, do process A 2 no matter what other actions are taken or what other conditions are met. 3. If condition C is met, do process A 3 no matter what other actions are taken or what other conditions are met. 4. If none of the conditions is met, then do processes A 1, A 2, and A 3 5. When more than one process is done, process A 1 must be done first, then A 2, and then A 3. The only permissible cases are: (A 1), (A 2), (A 3), (A 1, A 3), (A 2, A 3) and (A 1, A 2, A 3)

DECISION TABLES (HURL 83, VESS 86) 6. Decision Tables and Structure Figure 10. 2. A Troublesome Program.

PATH EXPRESSIONS AGAIN 1. General 1. The Model Logic-based testing is structural testing when it’s applied to structure

PATH EXPRESSIONS AGAIN 1. General 2. Predicates and Relational Operators A predicate is implemented as a process whose outcome is a truth-functional value. Don’t restrict your notion of predicate to arithmetic relations such as >, >=, =, <, <, ≠. Predicates are based on relational operators, of which the arithmetic relational operators are merely the most common

PATH EXPRESSIONS AGAIN 1. General 3. Case Statements and Multivalued Logics Predicates need not be restricted to binary truth values (TRUE/FALSE). There are multivalued logics such as Post-algebras that can be used to analyze such predicate structures, but their use is technically difficult and semantically tricky. Three-valued logics are used routinely at the hardware interfaces between chips to reduce the number signal lines needed.

PATH EXPRESSIONS AGAIN 1. General 4. What Goes Wrong with Predicates 1. The wrong relational operator is used: e. g. , > instead of <=. 2. The predicate expression of a compound predicate is incorrect: e. g. , A + B instead of AB. 3. The wrong operands are used: e. g. , A > X instead of A > Z. 4. The processing leading to the predicate (along the predicate’s interpretation path) is faulty.

PATH EXPRESSIONS AGAIN 2. Boolean Algebra. 1. Notation 1. Label each decision with an uppercase letter that represents the truth value of the predicate. The YES or TRUE branch is labeled with a letter and the NO or FALSE branch with the same letter overscored. 2. The truth value of a path is the product of the individual labels. Concatenation or products mean “AND. ” 3. If two or more paths merge at a node, the fact is expressed by use of a plus sign (+) which means “OR. ”

PATH EXPRESSIONS AGAIN 2. Boolean algebra 2. The Rules of Boolean Algebra Boolean algebra has three operators: × meaning AND. Also called multiplication. A statement such as AB means “A and B are both true. ” This symbol is usually left out as in ordinary algebra. + meaning OR. “A + B” means “either A is true or B is true or both. ” meaning NOT. Also negation or complementation. This is read as either “not A” or “A bar

PATH EXPRESSIONS AGAIN 2. Boolean algebra 2. The Rules of Boolean Algebra laws of boolean algebra:

PATH EXPRESSIONS AGAIN 2. Boolean algebra 3. Examples similarly

PATH EXPRESSIONS AGAIN 2. Boolean algebra 4. Paths and Domains Each predicate on the path is denoted by a capital letter (either overscored or not). Design, or specification such that there is one and only one product term for each domain: call these d 1, d 2, . . . di, . . . dm. Consider any two of these product terms, di and dj. For every i not equal to j, didj must equal zero.

PATH EXPRESSIONS AGAIN 2. Boolean algebra 5. Test Case Design 1. Simplest—Use any prime implicant in the expression to the point of interest as a basis for a path. The only values that must be taken are those that appear in the prime implicant. 2. Prime Implicant Cover—Pick input values so that there is at least one path for each prime implicant at the node of interest. 3. All Terms—Test all expanded terms for that node—for example, five terms for node 6, four for node 8, and four for node 12. That is, at least one path for each term. 4. Path Dependence—Because in general, the truth value of a predicate is obtained by interpreting the predicate, its value may depend on the path taken to get there. Do every term by every path to that term.

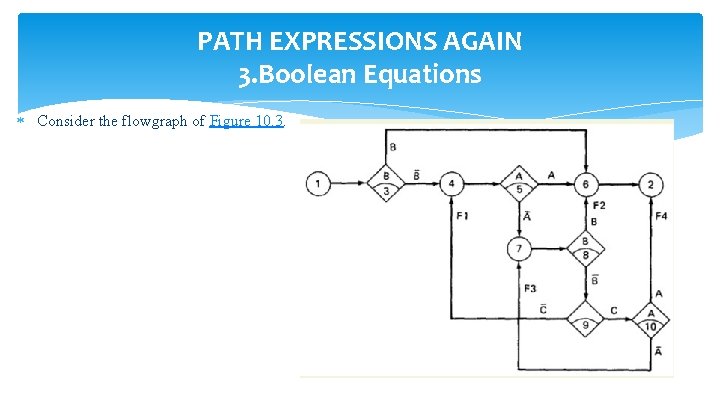
PATH EXPRESSIONS AGAIN 3. Boolean Equations Consider the flowgraph of Figure 10. 3.

PATH EXPRESSIONS AGAIN 3. Boolean Equations Equation for before flow graphs

KV CHARTS 1. The Problem If you had to deal with expressions in four, five, or six variables, you could get bogged down in the algebra and make as many errors in designing test cases as there are bugs in the routine you’re testing.

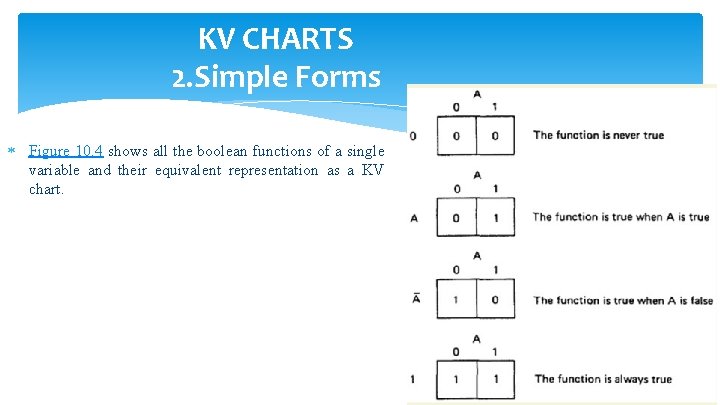
KV CHARTS 2. Simple Forms Figure 10. 4 shows all the boolean functions of a single variable and their equivalent representation as a KV chart.

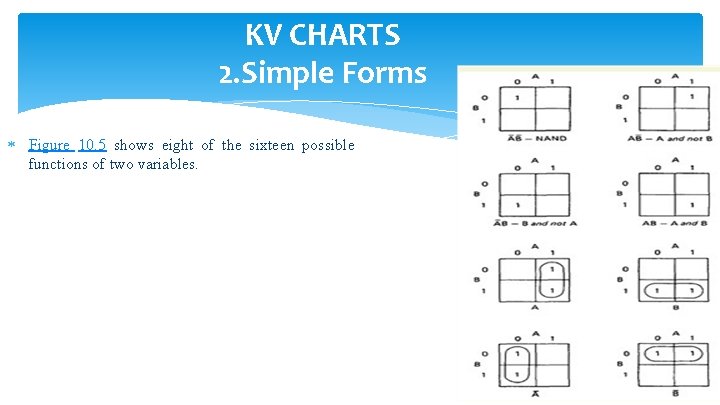
KV CHARTS 2. Simple Forms Figure 10. 5 shows eight of the sixteen possible functions of two variables.

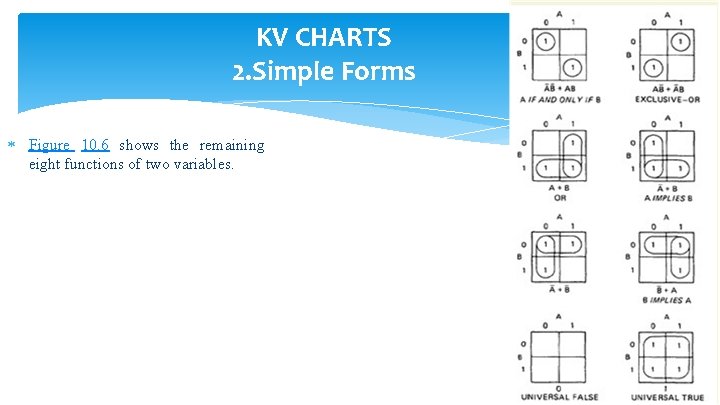
KV CHARTS 2. Simple Forms Figure 10. 6 shows the remaining eight functions of two variables.

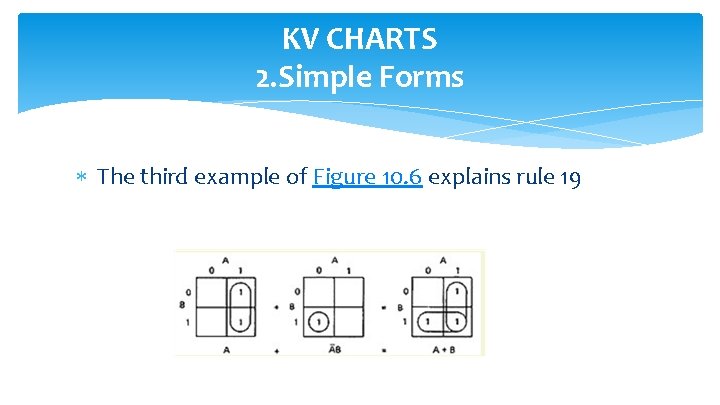
KV CHARTS 2. Simple Forms The third example of Figure 10. 6 explains rule 19

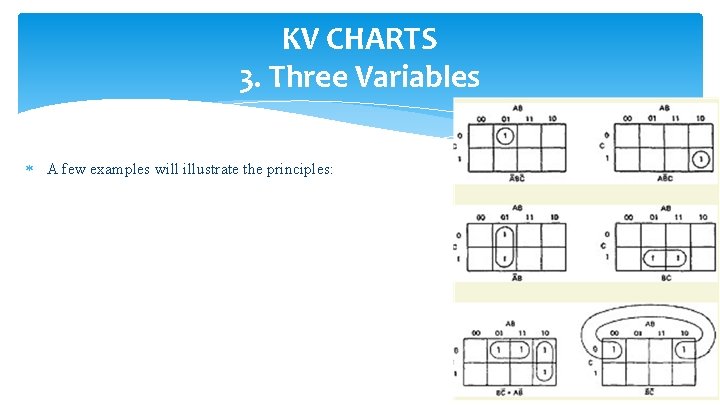
KV CHARTS 3. Three Variables A few examples will illustrate the principles:

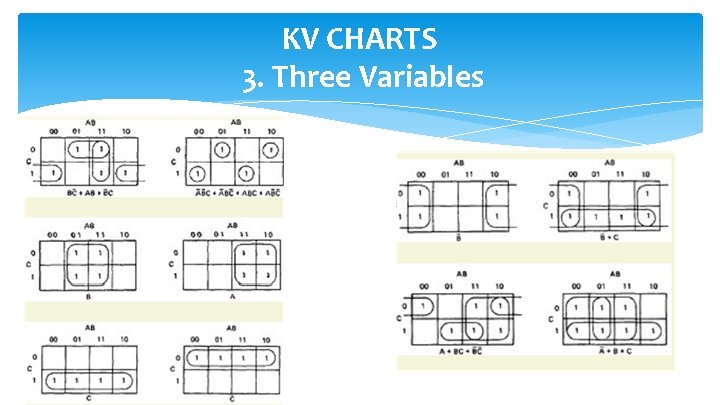
KV CHARTS 3. Three Variables

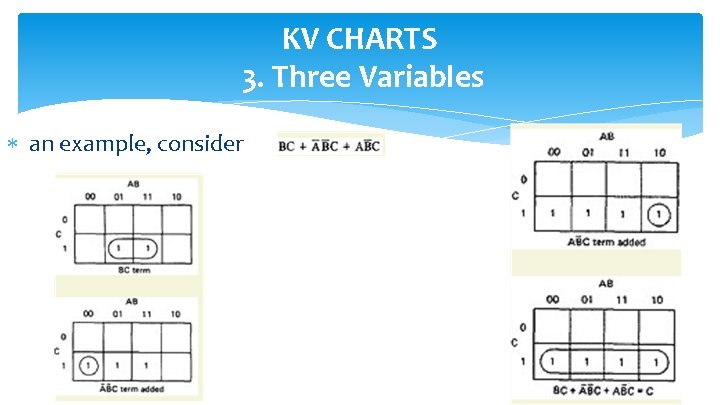
KV CHARTS 3. Three Variables an example, consider

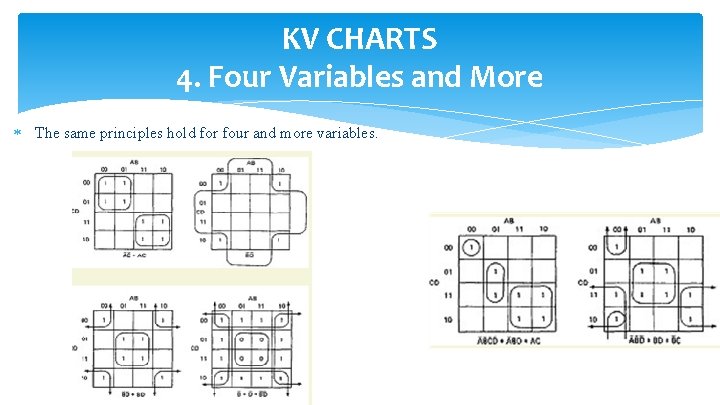
KV CHARTS 4. Four Variables and More The same principles hold for four and more variables.

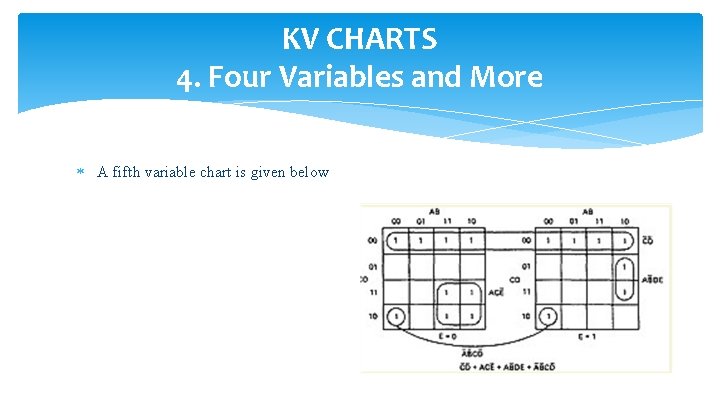
KV CHARTS 4. Four Variables and More A fifth variable chart is given below

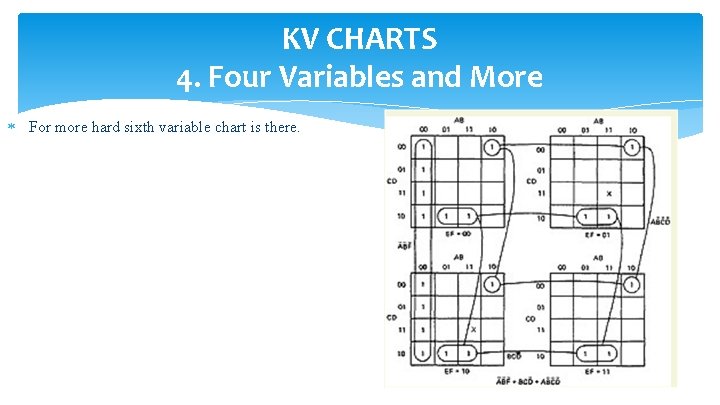
KV CHARTS 4. Four Variables and More For more hard sixth variable chart is there.

KV CHARTS 5. Even More Testing Strategies? 1. Use one prime implicant per domain. You’ll obviously miss parts of the domain not covered by the prime implicant you chose—e. g. , for disconnected domains. 2. Use the prime implicant with the fewest variables and work down to the prime implicant with the greatest number of variables 3. Overcome the obvious weaknesses of the above strategy (not all subdomains are covered) by using one test per prime implicant. 4. Every term in the product form for n variables has at most n literals but, because of simplifications made possible by adjacencies, terms may have fewer than n literals, say k. Any term with k literals can be expanded into two terms with k + 1 literals

SPECIFICATIONS 1. General The procedure for specification validation is straightforward: 1. Rewrite the specification using consistent terminology. 2. Identify the predicates on which the cases are based. Name them with suitable letters, such as A, B, C. 3. Rewrite the specification in English that uses only the logical connectives AND, OR, and NOT, however stilted it might seem. 4. Convert the rewritten specification into an equivalent set of boolean expressions.

SPECIFICATIONS 1. General 5. Identify the default action and cases, if any are specified. 6. Enter the boolean expressions in a KV chart and check for consistency. If the specifications are consistent, there will be no overlaps, except for cases that result in multiple actions. 7. Enter the default cases and check for consistency. 8. If all boxes are covered, the specification is complete. 9. If the specification is incomplete or inconsistent, translate the corresponding boxes of the KV chart back into English and get a clarification, explanation, or revision. 10. If the default cases were not specified explicitly, translate the default cases back into English and get a confirmation.

SPECIFICATIONS 2. Finding and Translating the Logic The specifications into sentences of the following form: “IF predicate THEN action. ” If—based on, based upon, because, but, if and when, only if, only when, provided that, when or if, whenever. Then—applies to, assign, consequently, do, implies that, infers that, initiate, means that, shall, should, then, will, would. And—all, and, as well as, both, but, in conjunction with, coincidental with, consisting of, comprising, either. . . or, furthermore, in addition to, including, jointly, moreover, mutually, plus, together with, total, with.

SPECIFICATIONS 2. Finding and Translating the Logic OR—and, and if . . . then, and/or, alternatively, any of, anyone of, as well as, but, case, contrast, depending upon, each, either. . . or, except if, conversely, failing that, furthermore, in addition to, nor, not only. . . but, although, other than, otherwise, or else, on the other hand, plus. NOT—but, but not, by contrast, besides, contrary, conversely, contrast, except if, excluding, excepting, fail, failing, less, neither, never, not, other than. EXCLUSIVE OR—but, by contrast, conversely, nor, on the other hand, other than, or. IMMATERIAL—independent of, irregardless, irrespective, irrelevant, regardless, but not if, whether or not.

SPECIFICATIONS 3. Ambiguities and Contradictions Spicification Is Here is the KV chart for this specification (I’ve used the numerals 1, 2, 3, and 4 to represent the actions and the default case):

SPECIFICATIONS 4. Don’t-Care and Impossible Terms There are only three things in this universe that certain are impossible: 1. Solving a provably unsolvable problem, such as creating a universal program verifier. 2. Knowing both the exact position and the exact momentum of a fundamental particle. 3. Knowing what happened before the “big bang” that started the universe. There are two kinds of so-called impossible conditions: (1) the condition cannot be created or is seemingly contradictory or improbable; (2) the condition results from our insistence on forcing a complex, continuous world into a binary, logical mold. Most program illogical conditions are of the latter kind. There are twelve cases for something, say, and we represent those cases by 4 bits.

SPECIFICATIONS 4. Don’t-Care and Impossible Terms 1. Identify all “impossible” and “illogical” cases and confirm them. 2. Document the fact that you intend to take advantage of them. 3. Fill out the KV chart with the possible cases and then fill in the impossible cases. Use the combined symbol φ, which is to be interpreted as a 0 or 1, depending on which value provides the greatest simplification of the logic. These terms are called don’t-care terms, because the case is presumed impossible, and we don’t care which value (0 or 1) is used.

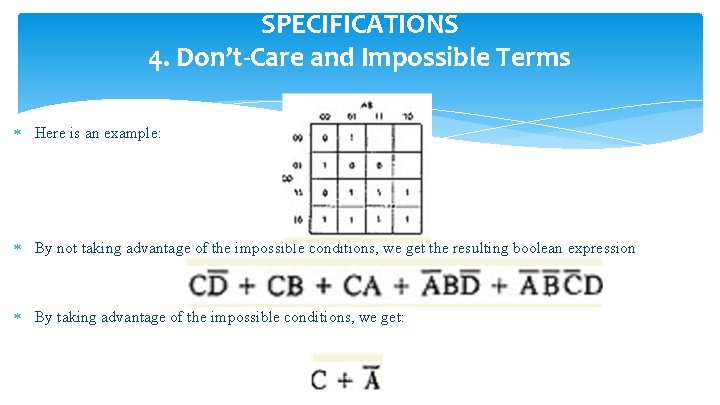
SPECIFICATIONS 4. Don’t-Care and Impossible Terms Here is an example: By not taking advantage of the impossible conditions, we get the resulting boolean expression By taking advantage of the impossible conditions, we get:

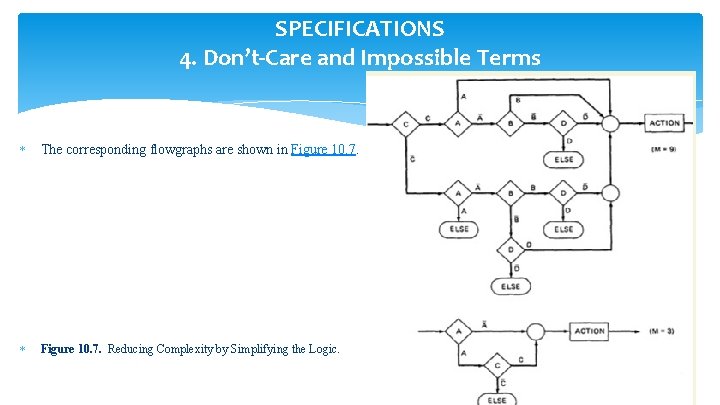
SPECIFICATIONS 4. Don’t-Care and Impossible Terms The corresponding flowgraphs are shown in Figure 10. 7. Reducing Complexity by Simplifying the Logic.

TESTABILITY TIPS The sensitization difficulties. 1. Identify your predicates (simple or compound). 2. If starting from code, get a branch covering set of path predicates. 3. Interpret the predicates so that they are expressed in terms of the input vector for the chosen path. 4. Simplify the path predicate expression for each selected path. If any expression is logically zero, the path is unachievable. Pick another path or paths to achieve branch coverage. 5. If any path predicate expression equals logical I then all other paths must be unachievable—find and fix the design bug. 6. The logical sum of the path predicate expressions must equal 1 or else there is an unsuspected loop, dangling code, or branch coverage is an inadequate test criterion.

TESTABILITY TIPS The canonical processor has three successive stages: 1. Predicate calculator. 2. Logic analyzer. 3. Domain processor.

TESTABILITY TIPS The canonical form, if it is achieved, has the following obvious advantages: 1. Branch coverage and all-paths coverage are identical. 2. All paths are achievable and easy to sensitize. 3. Separation simplifies maintenance.

Important 1. Reduce the following functions using K-Maps (16 M) ** F(A, B, C, D) = P(4, 5, 6, 7, 8, 12, 13)+d(1, 15) 2. Whether the predicates are restricted to binary truth-values or not. Explain. (10 M) 3. What are decision tables? Illustrate the applications of decision tables. How is a decision table useful in testing. Explain with an example. (16 M) ** 4. How can we determine paths in domains in Logic based testing? (8 M) 5. How the Boolean expression can be used in test case design (8 M) 6. Flow graphs are abstract representations of programs. Justify? (8 M)

Important 7. Explain prime implicant, sum of product form and product of sum form. (8 M) 8. How can we form specifications into sentences? Write down different phrases that can be used for words? (8 M) 9. Explain about the ambiguities and contradictions in specifications. ? (8 M) 10. Demonstrate by means of truth tables the validity of the following theorems of Boolean algebra: (8 M) ** i. Associative Laws ii. Demorgan's theorems for three variables iii. Distributive Law iv. Absorption Rule

To be continue……. . UNIT-7 STATES, STATE GRAPHS, AND TRANSITION TESTING