Solving Polynomial Equations PPT 5 3 2 Factor

Solving Polynomial Equations PPT 5. 3. 2

Factor Polynomial Expressions In the previous lesson, you factored various polynomial expressions. Groupi Refer to 5. 2. 2 in ng – Common Factor comm 2 to factor t Lesson he first on tw terms a review nd then owhich the last two strategy is terms. Such as: required for each question. 2 3 2 x – 2 x = x (x – 2) 3 – x 2 – 3 x + 3) 4 3 2 x(x x – 3 x + 3 x = 2(x – 1) – 3(x – 1)] x[x = Comm 2 – 3)(x – 1) on x(x Facto = r

Solving Polynomial Equations The expressions on the previous slide are now equations: y = x 3 – 2 x 2 and y = x 4 – x 3 – 3 x 2 +3 x To solve these equations, we will be solving for x when y = 0.

Solve y = x 3 – 2 x 2 0 = x 2(x – 2) Let y = 0 Common factor Separate the factors and set them equal to zero. x 2 = 0 or x – 2 = 0 x=2 Solve for x Therefore, the roots are 0 and 2.

Solve y = x 4 – x 3 – 3 x 2 + 3 x 0 = x(x 3 – x 2 – 3 x + 3) 0 =x[x 2(x – 1) – 3(x – 1)] 0 = x(x – 1)(x 2 – 3) Let y = 0 Common factor Group Separate the factors and set them equal to zero. x = 0 or x – 1 = 0 or x 2 – 3 = 0 x=1 x= Therefore, the roots are 0, 1 and ± 1. 73 Solve for x

What are you solving for? In the last two slides we solved for x when y = 0, which we call the roots. But what are roots? If you have a graphing calculator follow along with the next few slides to discover what the roots of an equation represent.

What are roots? Press the Y= button on your calculator. Type x 3 – 2 x 2

Press the GRAPH button. Look at where the graph is crossing the x-axis. The x-intercepts are 0 and 2. If you recall, when we solved for the roots of the equation y = x 3 – 2 x 2, we found them to be 0 and 2. Don’t forget, we also put 0 in for y, so it makes sense that the roots would be the x-intercepts.

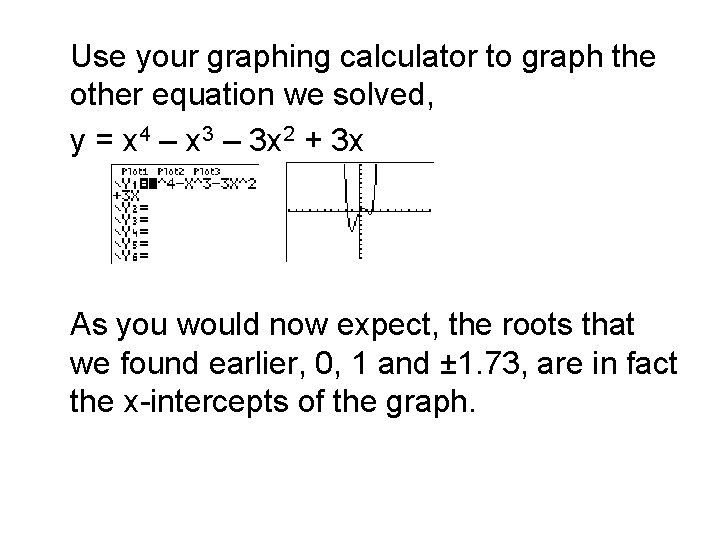
Use your graphing calculator to graph the other equation we solved, y = x 4 – x 3 – 3 x 2 + 3 x As you would now expect, the roots that we found earlier, 0, 1 and ± 1. 73, are in fact the x-intercepts of the graph.

The Quadratic Formula For equations in quadratic form: ax 2 + bx + c = 0, we can use the quadratic formula to solve for the roots of the equation. This equation is normally used when factoring is not an option.

Using the Quadratic Formula Solve the following cubic equation: Can this. We equation still need to solve for x y = x 3 + 5 x 2 – 9 x be factored? here. Can this equation be 2 0= x(xit can + 5 x– – 9) YES factored? factor. x =common 0 x 2 + 5 x – 9 = 0 No. There are nouse twothe quadratic formula. We can, however, integers that will multiply a=1 to -9 and add to 5. b=5 c = -9 Remember, the root 0 came from an earlier step. Therefore, the roots are 0, 6. 41 and -1. 41.