Solving Polynomial Equations of HIGHER Degree Factor Polynomial








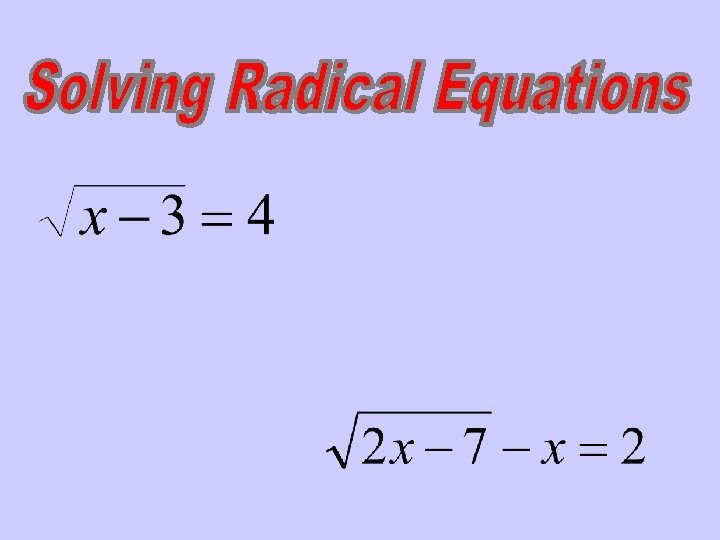
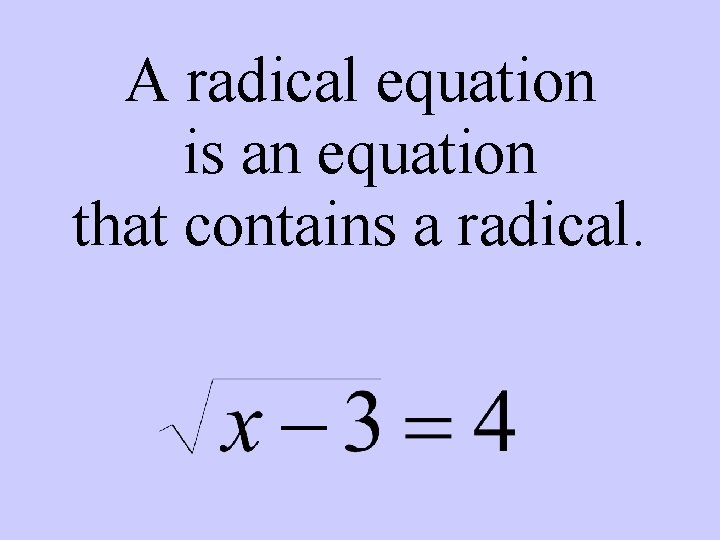
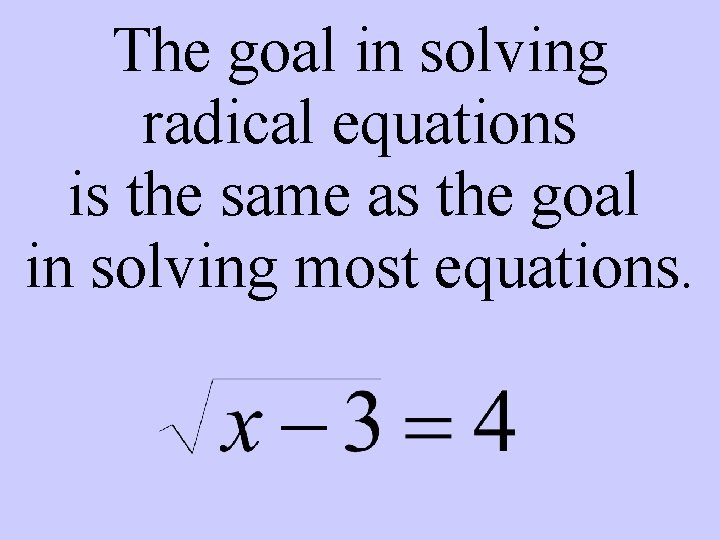
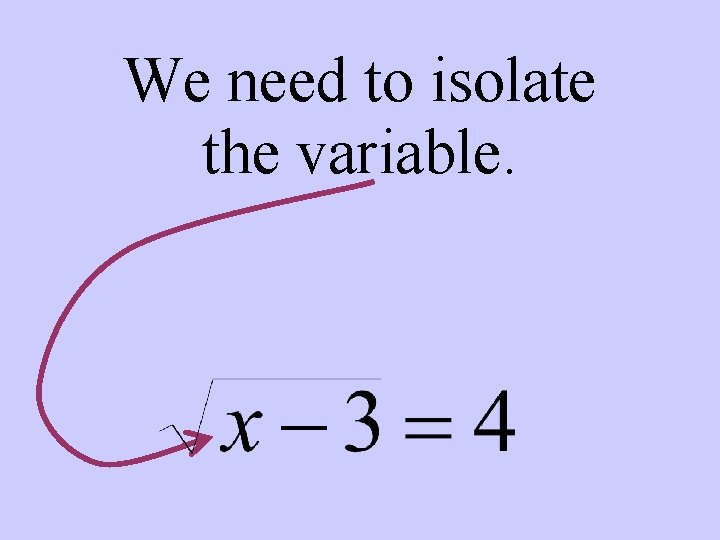

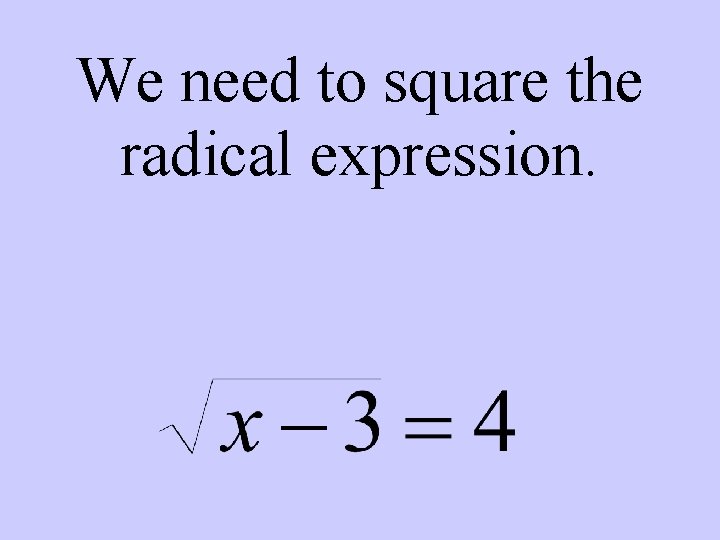
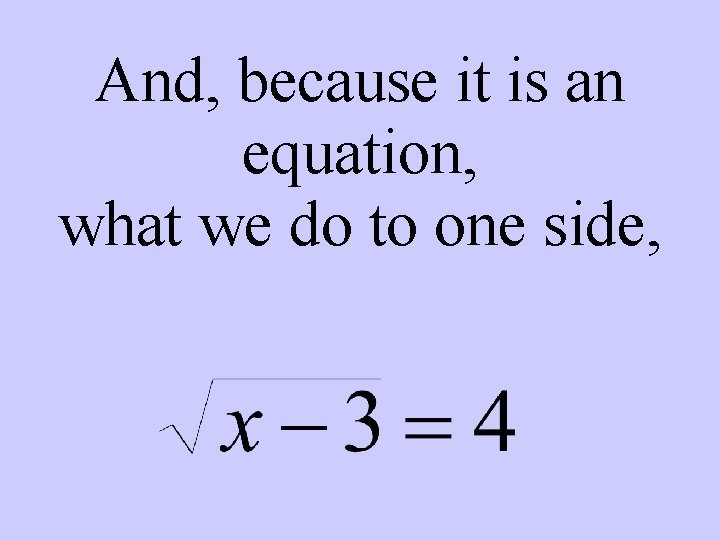
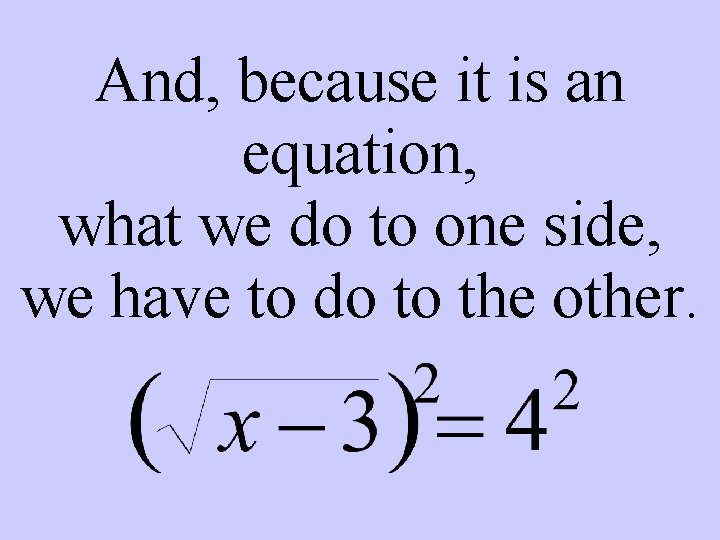
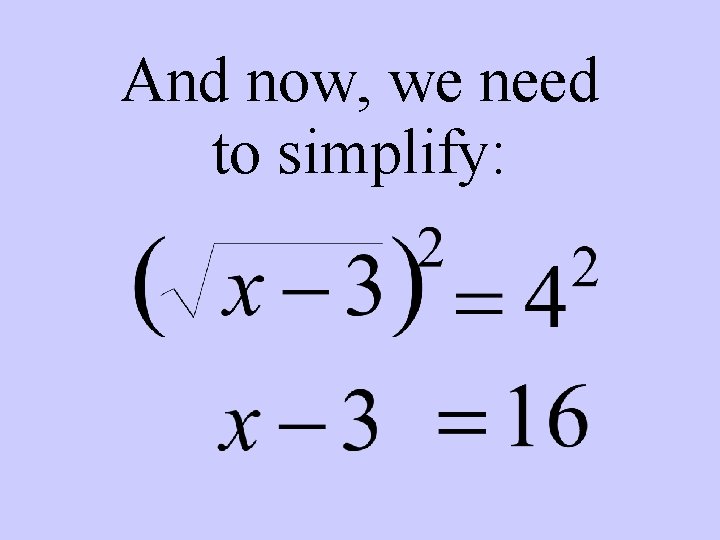
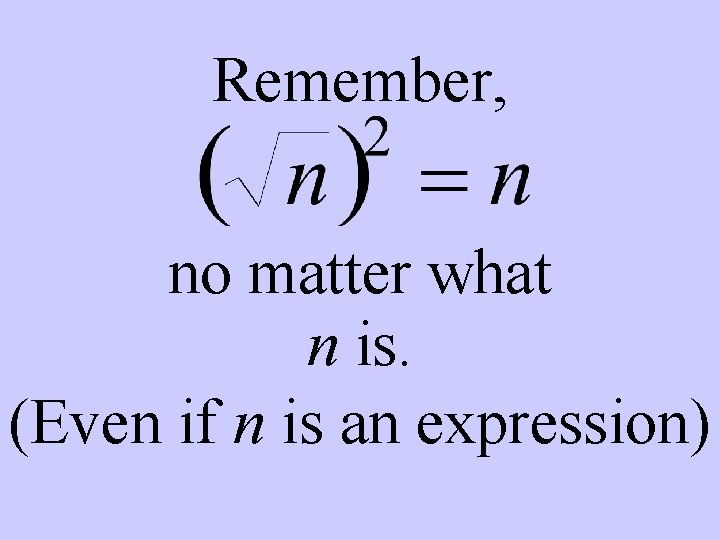
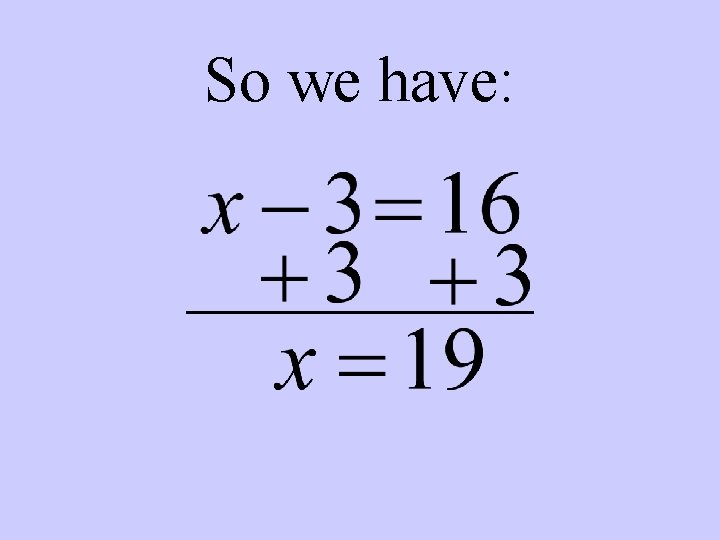

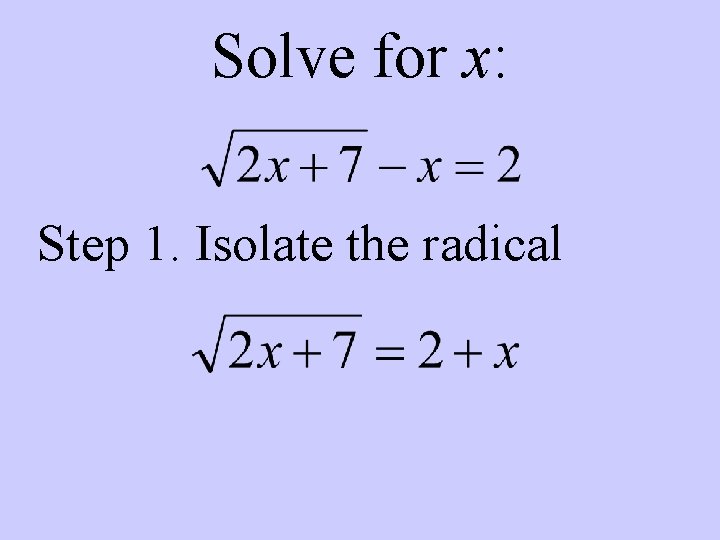
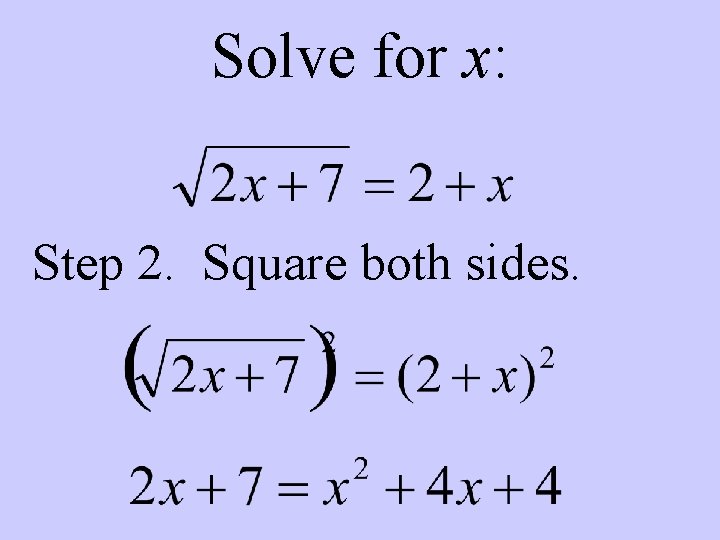
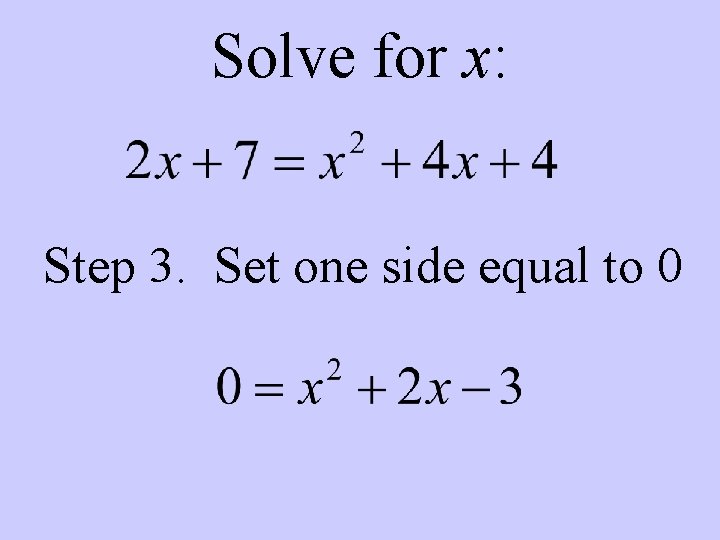
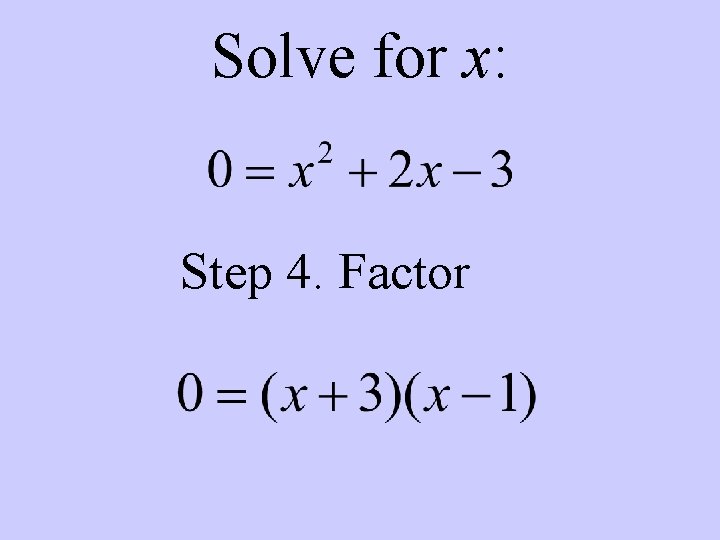
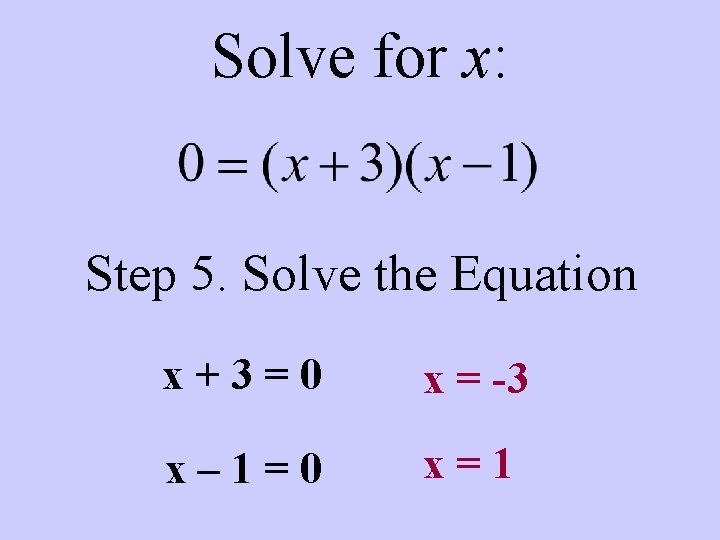


- Slides: 27


Solving Polynomial Equations of HIGHER Degree

Factor Polynomial Expressions The methods we learned can also be used to solve polynomial degree Commonequations of higher Grouping – take Factor common factor out of the first two terms and the last two terms. 2(x – 2) x – = x 4 – x 3 – 3 x 2 + 3 x = x(x 3 – x 2 – 3 x + 3) = x[x 2(x – 1) – 3(x – 1)] Comm 2 – 3)(x – 1) on x(x = Facto r x 3 2 x 2

Solving Polynomial Equations The expressions on the previous slide are now equations: y= x 3 – 2 x 2 and y= x 4 – x 3 – 3 x 2 +3 x We will be solving for x when y = 0.

Solve y = x 3 – 2 x 2 0 = x 2(x – 2) Let y = 0 Common factor Separate the factors and set them equal to zero. x 2 = 0 or x – 2 = 0 x=2 Solve for x Therefore, the solutions are 0 and 2.

Solve Let y = 0 y = x 4 – x 3 – 3 x 2 + 3 x 0 = x(x 3 – x 2 – 3 x + 3) 0 =x[x 2(x – 1) – 3(x – 1)] 0 = x(x – 1)(x 2 – 3) Common factor Group Separate the factors and set them equal to zero. Solve for x x = 0 or x – 1 = 0 or x 2 – 3 = 0 x=1 x= Therefore, the solutions are 0, 1 and ± 1. 73

Using the Quadratic Formula Solve the following cubic equation: equation still need to solve for x y = x 3 + 5 x 2 – 9 x Can this. We be factored? here. Can this equation be 2 it can – – 9) 0 YES = x(x + 5 x factored? factor. xcommon =0 x 2 + 5 x – 9 = 0 are no two We. No. can, There however, use the quadratic formula. integers that will multiply a=1 to -9 and add to 5. Remember, the solution 0 came from an earlier step. b=5 c = -9 Therefore, the solutions are 0 and -5±√ 61 2

Now… Solving Radical Expressions
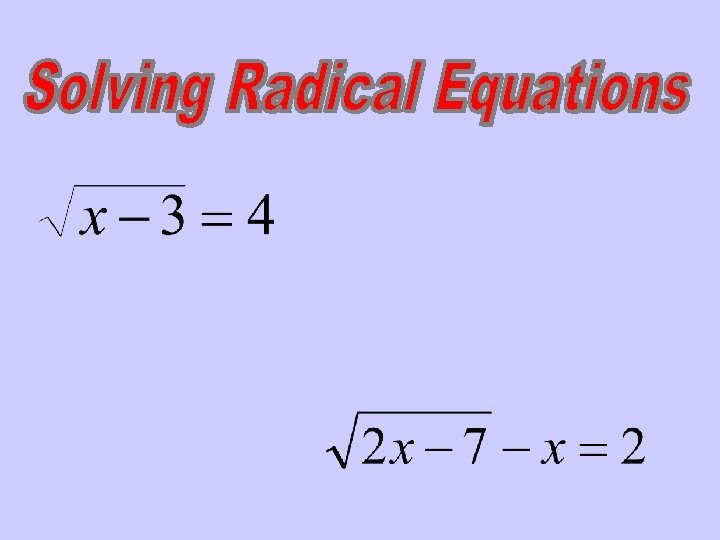
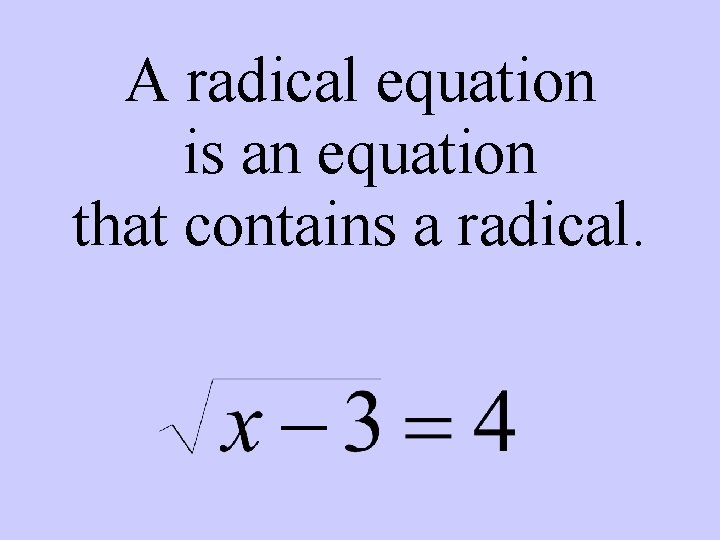
A radical equation is an equation that contains a radical.
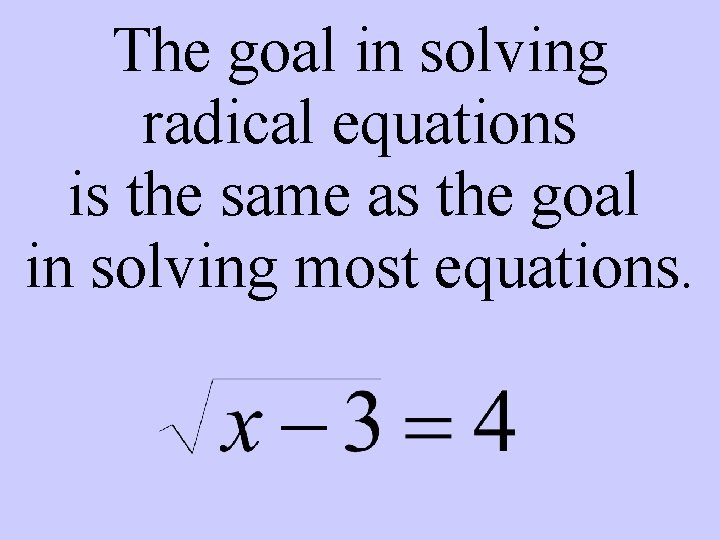
The goal in solving radical equations is the same as the goal in solving most equations.
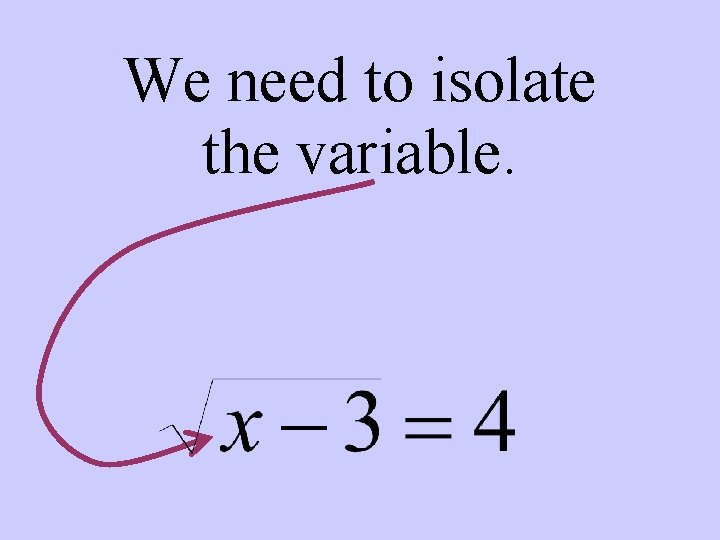
We need to isolate the variable.

But there is only one way to move the variable out from under the square root sign.
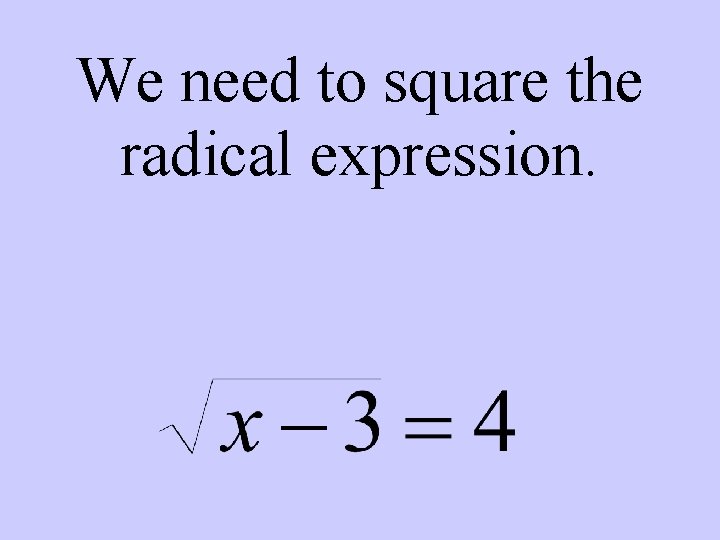
We need to square the radical expression.
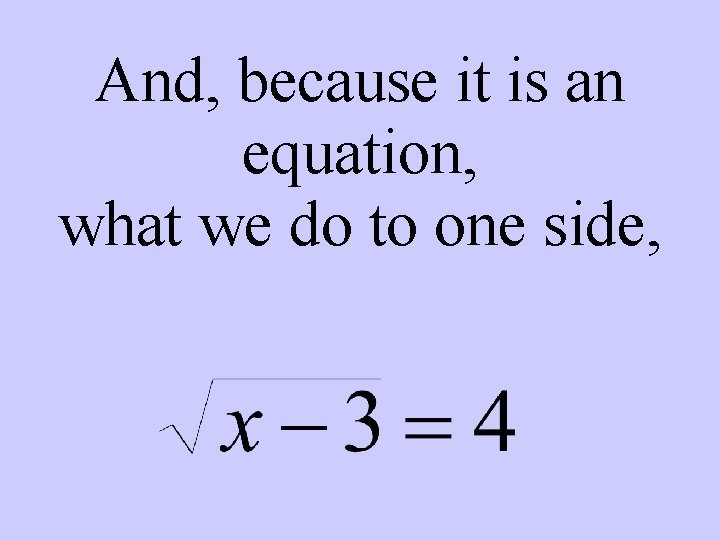
And, because it is an equation, what we do to one side,
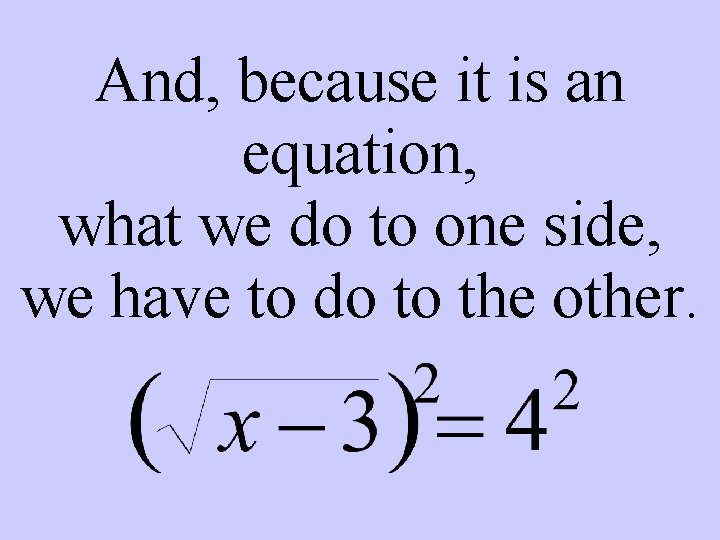
And, because it is an equation, what we do to one side, we have to do to the other.
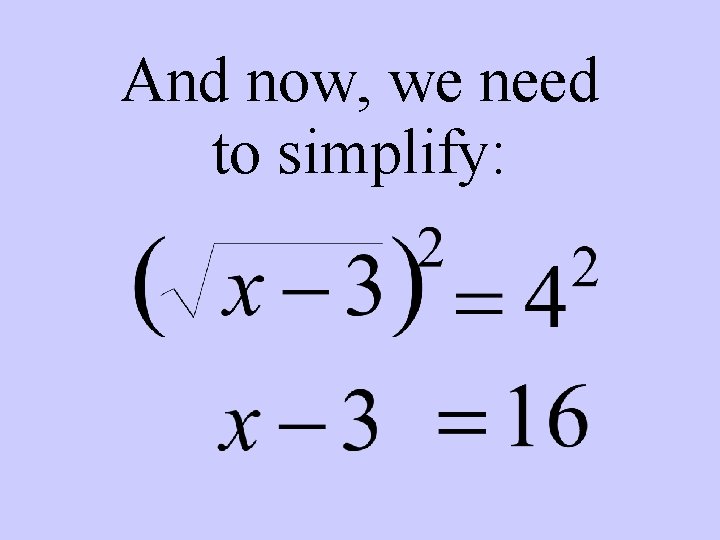
And now, we need to simplify:
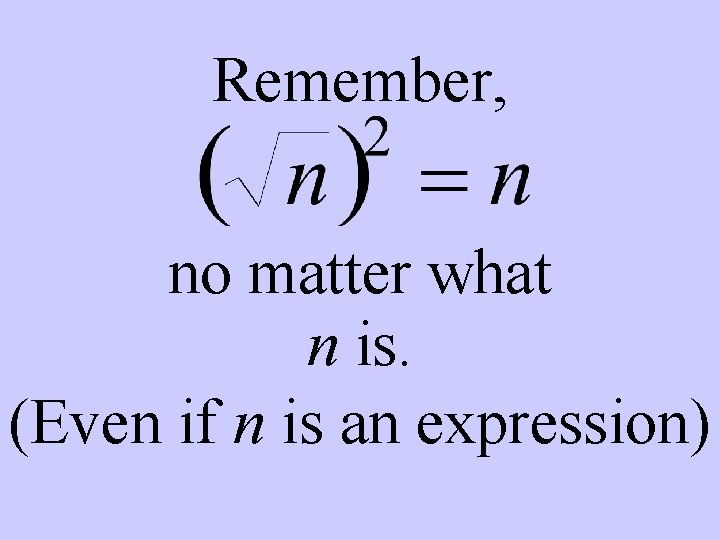
Remember, no matter what n is. (Even if n is an expression)
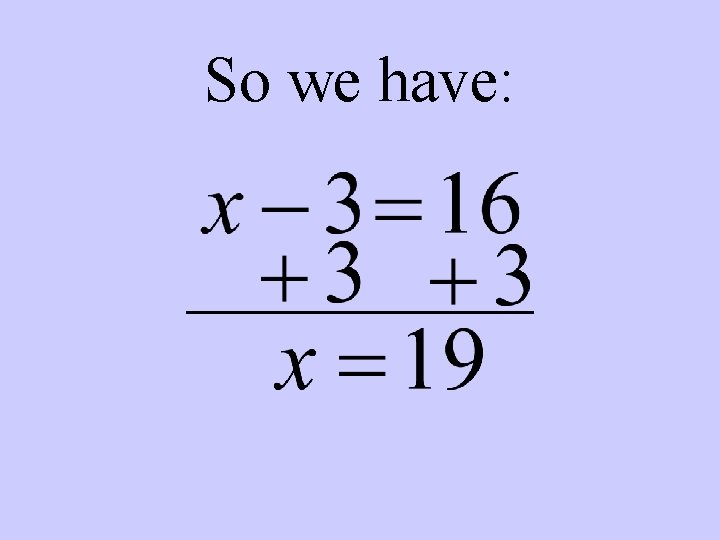
So we have:

Another Example:
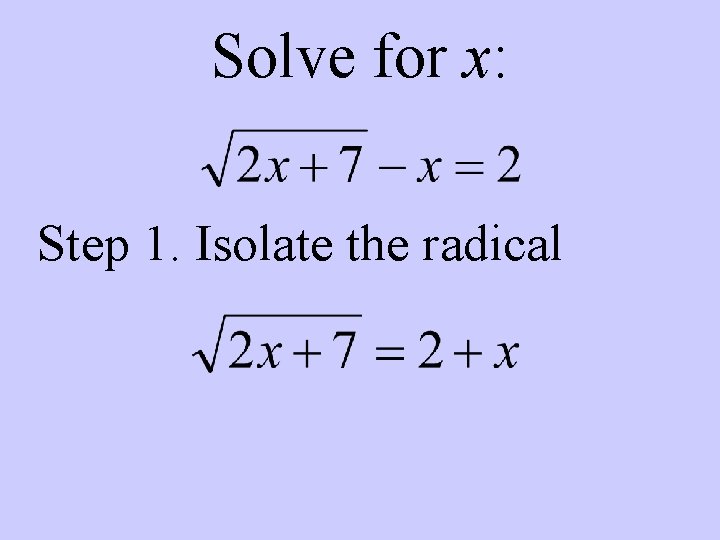
Solve for x: Step 1. Isolate the radical
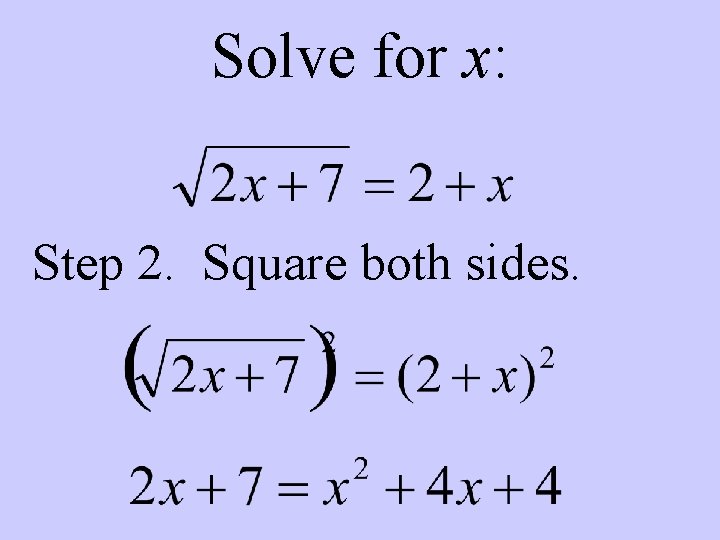
Solve for x: Step 2. Square both sides.
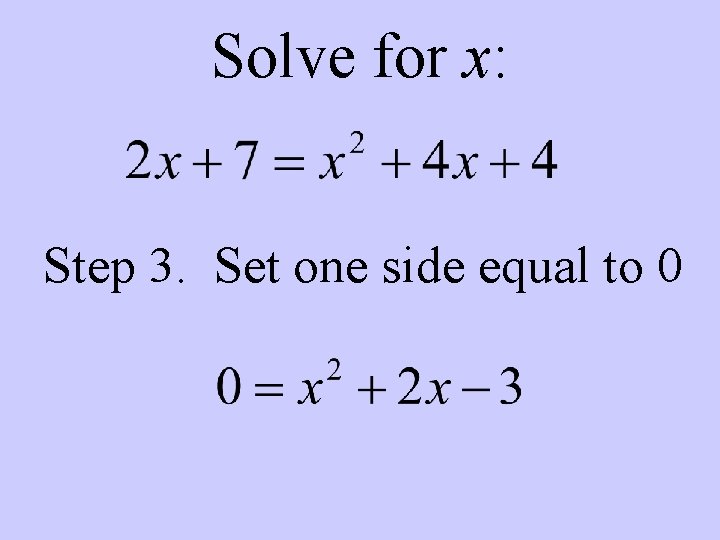
Solve for x: Step 3. Set one side equal to 0
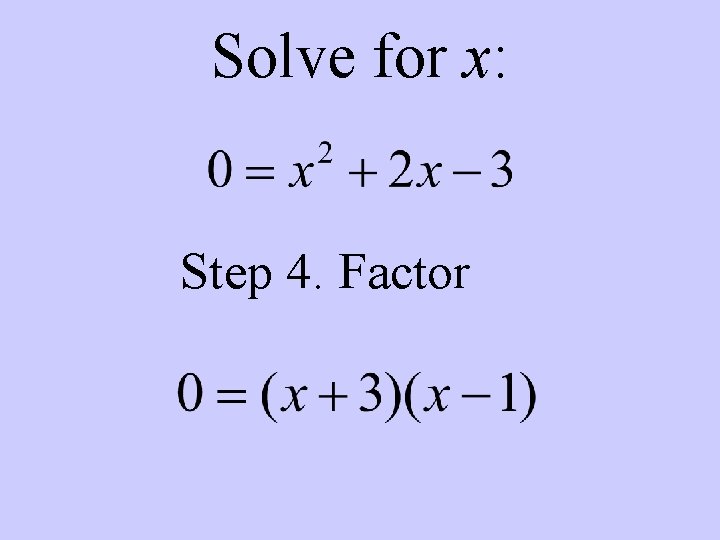
Solve for x: Step 4. Factor
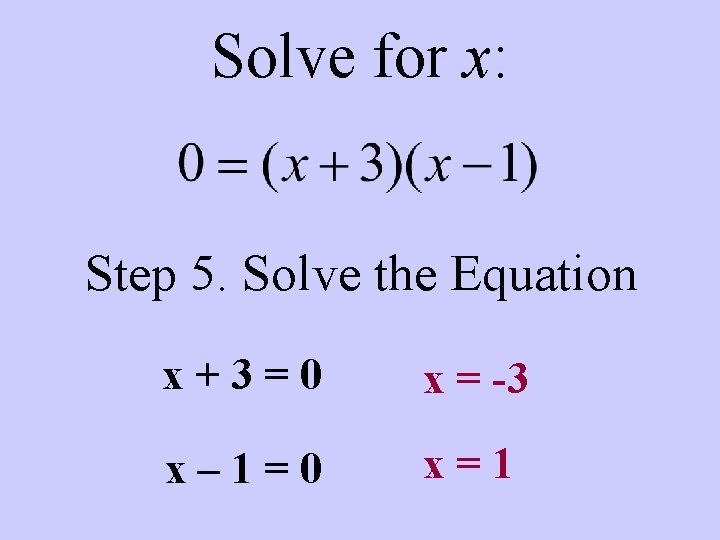
Solve for x: Step 5. Solve the Equation x+3=0 x = -3 x– 1=0 x=1

Classwork: • Punchline 13. 13 • Factoring Summary Worksheet • Sheet 28

Homework: Textbook Pg 24 – 25 Exercises: 87, 88, 89, 91, 92, 96, 97, 99, 102, 106, 109