Ch 6 4 Solving Polynomial Equations Sum and

Ch. 6. 4 Solving Polynomial Equations

Sum and Difference of Cubes

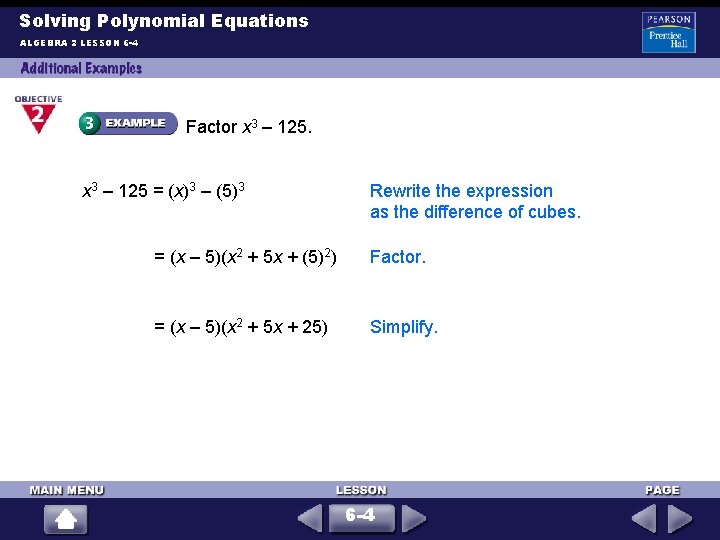
Solving Polynomial Equations ALGEBRA 2 LESSON 6 -4 Factor x 3 – 125 = (x)3 – (5)3 Rewrite the expression as the difference of cubes. = (x – 5)(x 2 + 5 x + (5)2) Factor. = (x – 5)(x 2 + 5 x + 25) Simplify. 6 -4

P. 322 Check understanding # 3

Solving Polynomial Equations ALGEBRA 2 LESSON 6 -4 Solve 8 x 3 + 125 = 0. Find all complex roots. 8 x 3 + 125 = (2 x)3 + (5)3 Rewrite the expression as the difference of cubes. = (2 x + 5)((2 x)2 – 10 x + (5)2) Factor. = (2 x + 5)(4 x 2 – 10 x + 25) Simplify. 5 2 Since 2 x + 5 is a factor, x = – is a root. The quadratic expression 4 x 2 – 10 x + 25 cannot be factored, so use the Quadratic Formula to solve the related quadratic equation 4 x 2 – 10 x + 25 = 0. 6 -4

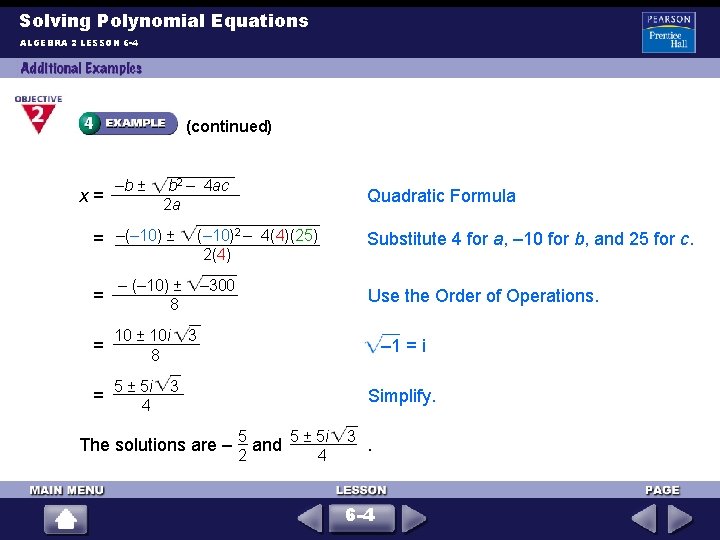
Solving Polynomial Equations ALGEBRA 2 LESSON 6 -4 (continued) –b ± b 2 – 4 ac x = 2 a Quadratic Formula = –(– 10) ± (– 10)2 – 4(4)(25) Substitute 4 for a, – 10 for b, and 25 for c. 2(4) = – (– 10) ± – 300 8 = 10 ± 10 i 3 8 = 5 ± 5 i 3 4 Use the Order of Operations. – 1 = i Simplify. 5 5 ± 5 i 3 The solutions are – and . 2 4 6 -4

P. 323 # 4 B

Solving Polynomial Equations ALGEBRA 2 LESSON 6 -4 Factor x 4 – 6 x 2 – 27. Step 1: Since x 4 – 6 x 2 – 27 has the form of a quadratic expression, you can factor it like one. Make a temporary substitution of variables. x 4 – 6 x 2 – 27 = (x 2)2 – 6(x 2) – 27 = a 2 – 6 a – 27 Rewrite in the form of a quadratic expression. Substitute a for x 2. Step 2: Factor a 2 – 6 a – 27 = (a + 3)(a – 9) Step 3: Substitute back to the original variables. (a + 3)(a – 9) = (x 2 + 3)(x 2 – 9) = (x 2 + 3)(x – 3) Substitute x 2 for a. Factor completely. The factored form of x 4 – 6 x 2 – 27 is (x 2 + 3)(x – 3). 6 -4

p. 323 Check Understanding # 5 B

Solving Polynomial Equations ALGEBRA 2 LESSON 6 -4 Solve x 4 – 4 x 2 – 45 = 0 (x 2)2 – 4(x 2) – 45 = 0 Write in the form of a quadratic expression. Think of the expression as a 2 – 4 a – 45, which factors as (a – 9)(a + 5). (x 2 – 9)(x 2 + 5) = 0 (x – 3)(x + 3)(x 2 + 5) = 0 x = 3 or x = – 3 or x 2 = – 5 Use the factor theorem. x = ± 3 or x = ± i 5 Solve for x, and simplify. 6 -4

Homework Page 324, #: 1, 2, 8, 9, 13 -31 odd