Section 5 1 Solving Polynomial Equations 1 POLYNOMIAL



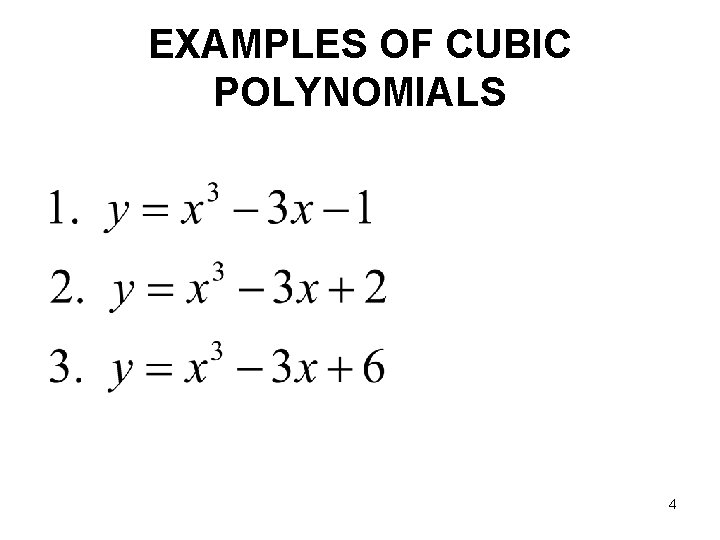



- Slides: 9

Section 5. 1 Solving Polynomial Equations 1

POLYNOMIAL EQUATIONS In Chapter 1, we solved linear (first-degree) polynomial equations. In Chapter 2, we solved quadratic (second-degree) polynomial equations. In Chapter 2, we also mentioned polynomials with higher-degree. In this section, we want to learn to solve higher-degree polynomials. We also want to see how polynomials of higherdegree can be applied to real-world situations 2

CUBIC POLYNOMIALS A cubic (third-degree) polynomial equation has the form ax 3 + bx 2 + cx + d = 0. A cubic polynomial can have as many as three real number solutions. 3
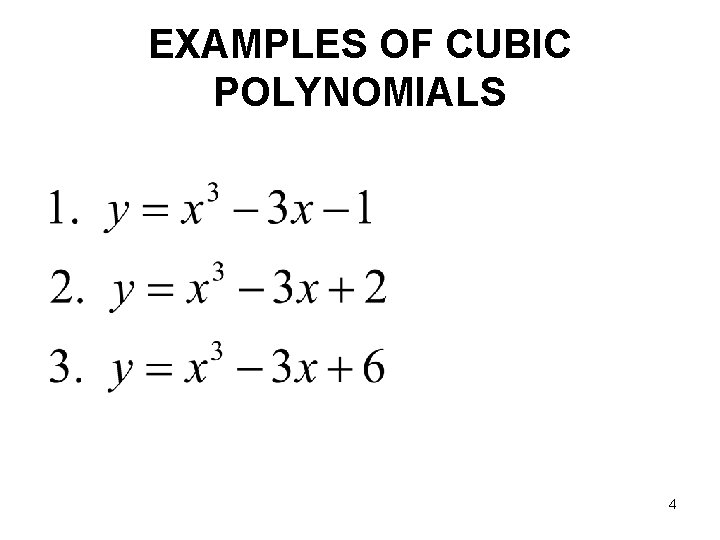
EXAMPLES OF CUBIC POLYNOMIALS 4

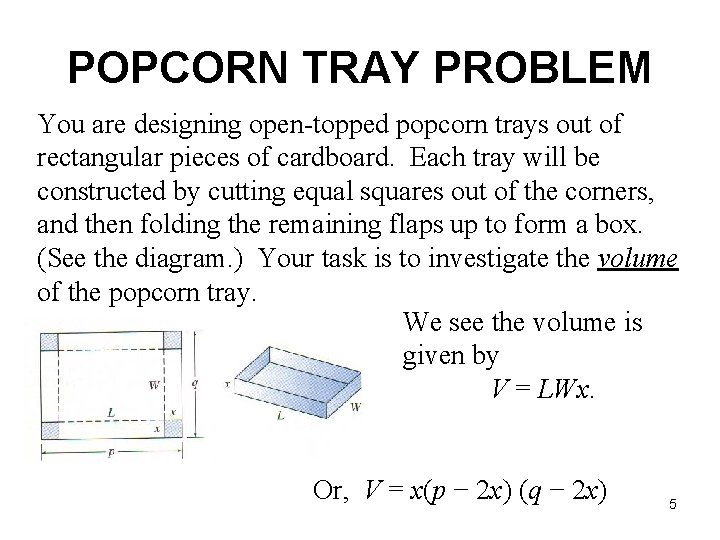
POPCORN TRAY PROBLEM You are designing open-topped popcorn trays out of rectangular pieces of cardboard. Each tray will be constructed by cutting equal squares out of the corners, and then folding the remaining flaps up to form a box. (See the diagram. ) Your task is to investigate the volume of the popcorn tray. We see the volume is given by V = LWx. Or, V = x(p − 2 x) (q − 2 x) 5

EXAMPLE Starting with a 15 cm by 35 cm sheet of cardboard, a popcorn tray is constructed. If the volume is to be precisely 450 cm 3, what are the dimensions of the popcorn tray? 6

QUARTIC POLYNOMIALS A quartic (fourth-degree) polynomial equation has the form ax 4 + bx 3 + cx 2 + dx + e = 0. A quartic equation can have as many as four real number solutions. 7

EXAMPLES OF QUARTIC POLYNOMIALS A quartic polynomial has • three or fewer bends (turning points) • four or fewer real-number zeros. 8

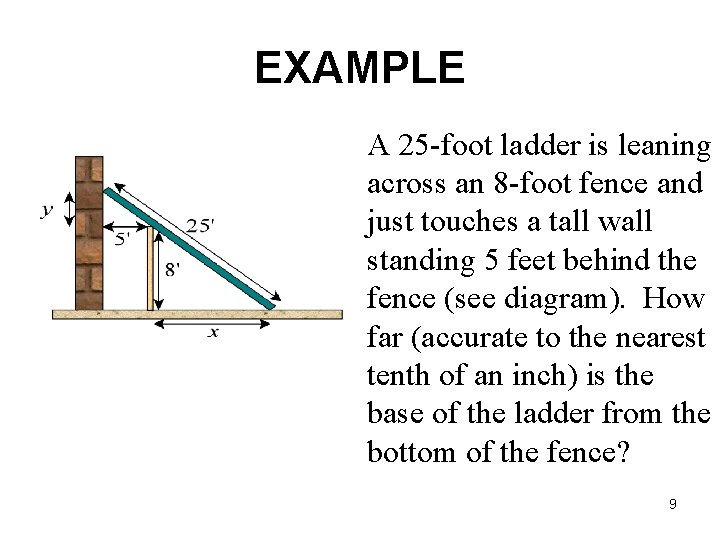
EXAMPLE A 25 -foot ladder is leaning across an 8 -foot fence and just touches a tall wall standing 5 feet behind the fence (see diagram). How far (accurate to the nearest tenth of an inch) is the base of the ladder from the bottom of the fence? 9