Multiples factors and primes 1 of 53 Boardworks

Multiples, factors and primes 1 of 53 © Boardworks Ltd 2004

Contents N 3 Multiples, factors and primes N 3. 1 Divisibility N 3. 2 Multiples and factors N 3. 3 Prime numbers N 3. 4 Prime factor decomposition N 3. 5 HCF and LCM 2 of 53 © Boardworks Ltd 2004

Divisibility by 2 Is 367 908 divisible by 2? 367 908 is divisible by 2 if 2 divides into it exactly without leaving any remainders. We can tell if a number is divisible by 2 by looking at the last digit in the number. A number is divisible by 2 if the last digit is 0, 2, 4, 6 or 8. Yes, 367 908 is divisible by 2. It is an even number. 3 of 53 © Boardworks Ltd 2004

Divisibility by 3 Is 35 841 divisible by 3? We can tell if a number is divisible by 3 by adding together its digits. This is called finding the digit sum. A number is divisible by 3 if the digit sum is divisible by 3. The digit sum of 35 841 is 3 + 5 + 8 + 4 + 1 = 21 21 is divisible by 3. Yes, 35 841 is divisible by 3. 4 of 53 © Boardworks Ltd 2004

Divisibility by 4 Is 1 934 274 divisible by 4? We can tell if a number is divisible by 4 by looking at the last two digits in the number. A number is divisible by 4 if the last two digits are divisible by 4. A two-digit number is divisible by 4: if it ends in 0, 4 or 8 and the first digit is even if it ends in 2 or 6 and the first digit is odd. No, 1 934 274 is not divisible by 4. 5 of 53 © Boardworks Ltd 2004

Divisibility by 5 Is 231 030 divisible by 5? We can tell if a number is divisible by 5 by looking at the last digit in the number. A number is divisible by 5 if the last digit is 0 or 5. Yes, 231 030 is divisible by 5. 6 of 53 © Boardworks Ltd 2004

Divisibility by 6 Is 53 702 divisible by 6? We can tell if a number is divisible by 6 by looking at its last digit and finding its digit sum. A number is divisible by 6 if it is divisible by both 2 and 3. The last digit in 53 702 is a 2 and so it is divisible by 2. The digit sum of 53 702 is 5 + 3 + 7 + 0 + 2 = 17 17 is not divisible by 3 and so 53 702 is not divisible by 3. 53 703 No, 53 702 is divisible is not divisible by 6 only byif 6. it is divisible by both 2 and 3. 7 of 53 © Boardworks Ltd 2004

Divisibility by 8 Is 63 072 divisible by 8? We can tell if a number is divisible by 8 by halving it and checking for divisibility by 4. A number is divisible by 8 if half of it is divisible by 4. Half of 63 072 is 31 536 Look at the last two digits. 36 is divisible by 4. Yes, 63 072 is divisible by 8. 8 of 53 © Boardworks Ltd 2004

Divisibility by 9 Is 6 874 275 divisible by 9? We can tell if a number is divisible by 9 by finding its digit sum. A number is divisible by 9 if its digit sum is divisible by 9. The digit sum of 6 873 975 is 6 + 8 + 7 + 3 + 9 + 7 + 5 = 45 45 is divisible by 9. Yes, 6 873 975 is divisible by 9. 9 of 53 © Boardworks Ltd 2004

Divisibility by 10 Is 6 311 289 divisible by 10? We can tell if a number is divisible by 10 by looking at the last digit in the number. A number is divisible by 10 if the last digit is 0. No, 6 311 289 is not divisible by 10. 10 of 53 © Boardworks Ltd 2004

Divisibility by larger numbers Is 214 875 divisible by 15? We test for divisibility by some larger numbers by using two simpler tests. A number is divisible by 15 if it is divisible by both 3 and 5. The digit sum of 214 875 is 2 + 1 + 4 + 8 + 7 + 5 = 27 27 is divisible by 3 and so 214 875 is divisible by 3. The last digit in 214 875 is a 5 and so it is also divisible by 5. Yes, 214 875 is divisible by 15. 11 of 53 © Boardworks Ltd 2004

Divisibility by larger numbers We can check for divisibility by other larger numbers by testing for divisibility by factors of the number. For example, A number is divisible by 12 if it is divisible by both 3 and 4. A number is divisible by 15 if it is divisible by both 3 and 5. A number is divisible by 18 if it is divisible by both 2 and 9. A number is divisible by 20 if it is divisible by both 4 and 5. A number is divisible by 24 if it is divisible by both 3 and 8. A number is divisible by 30 if it is divisible by both 3 and 10. 12 of 53 © Boardworks Ltd 2004

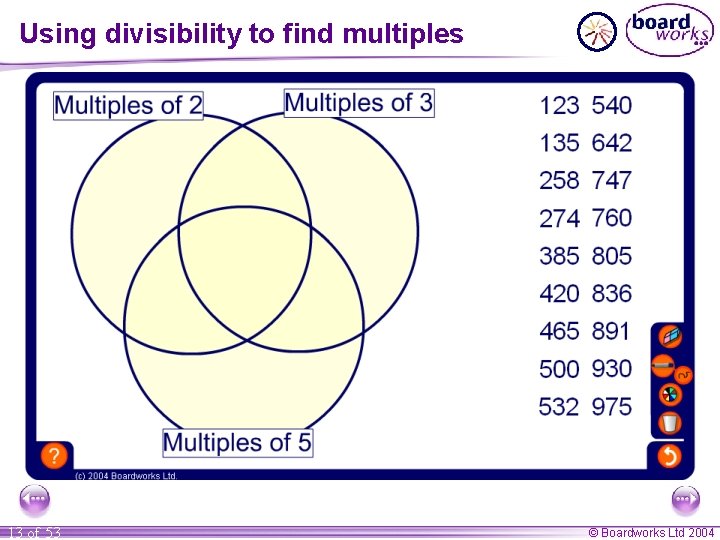
Using divisibility to find multiples 13 of 53 © Boardworks Ltd 2004

Contents N 3 Multiples, factors and primes N 3. 1 Divisibility N 3. 2 Multiples and factors N 3. 3 Prime numbers N 3. 4 Prime factor decomposition N 3. 5 HCF and LCM 14 of 53 © Boardworks Ltd 2004

Multiples A multiple of a number is found by multiplying the number by any whole number. What are the first six multiples of 4? To find the first six multiples of 4 multiply 4 by 1, 2, 3, 4, 5 and 6 in turn to get: 4, 8, 12, 16, 20 and 24. Any given number has infinitely many multiples. 15 of 53 © Boardworks Ltd 2004

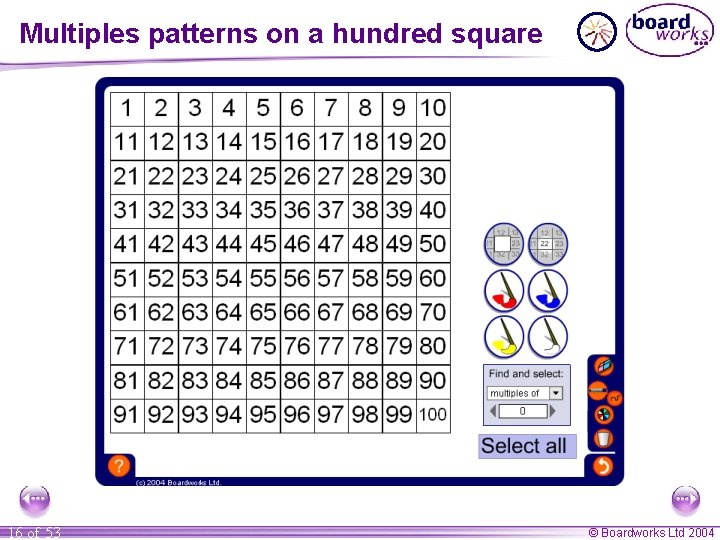
Multiples patterns on a hundred square 16 of 53 © Boardworks Ltd 2004

Rectangular arrangements 17 of 53 © Boardworks Ltd 2004

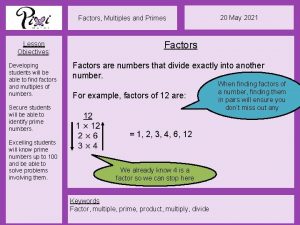
Finding factors A factor of a number is a whole number that divides exactly into a given number. Factors come in pairs. For example, what are the factors of 30? 1 and 30, 2 and 15, 3 and 10, 5 and 6. So, in order, the factors of 30 are: 1, 2, 3, 5, 6, 10, 15 and 30. 18 of 53 © Boardworks Ltd 2004

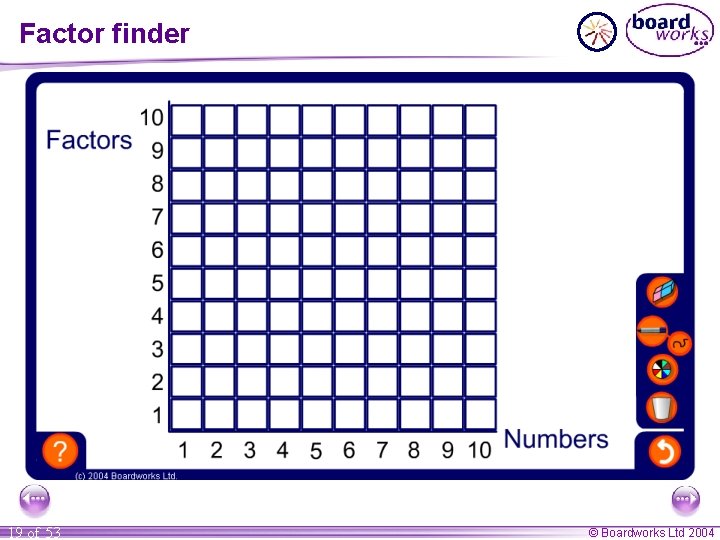
Factor finder 19 of 53 © Boardworks Ltd 2004

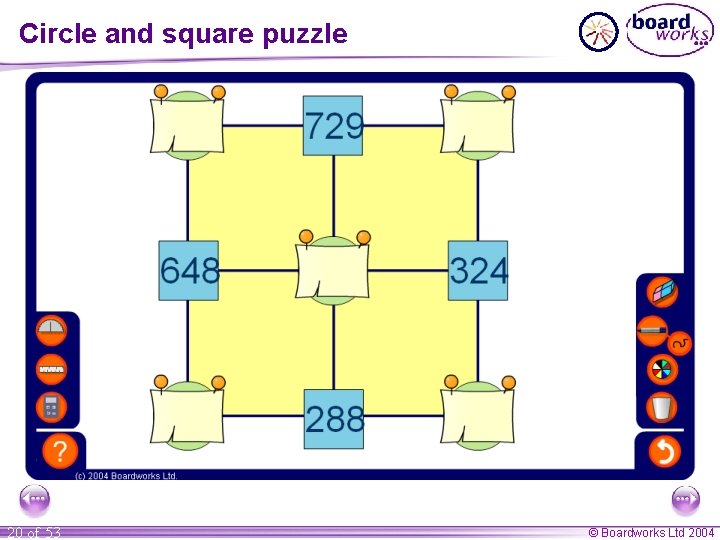
Circle and square puzzle 20 of 53 © Boardworks Ltd 2004

Contents N 3 Multiples, factors and primes N 3. 1 Divisibility N 3. 2 Multiples and factors N 3. 3 Prime numbers N 3. 4 Prime factor decomposition N 3. 5 HCF and LCM 21 of 53 © Boardworks Ltd 2004

Sieve of Eratosthenes 22 of 53 © Boardworks Ltd 2004

Prime numbers If a whole number has two, and only two, factors it is called a prime number. For example, the number 17 has only two factors, 1 and 17. Therefore, 17 is a prime number. The number 1 has only one factor, 1. Therefore, 1 is not a prime number. There is only one even prime number. What is it? 2 is the only even prime number. 23 of 53 © Boardworks Ltd 2004

Prime numbers The first 10 prime numbers are: 2 24 of 53 3 5 7 11 13 17 19 23 29 © Boardworks Ltd 2004

Testing for prime numbers Is 107 a prime number? We can check whether or not a number is prime by testing for divisibility by successive numbers. Is 107 divisible by 2? The last digit is a 7 so, no. Is 107 divisible by 3? The digit sum is 8 so, no. We don’t need to check for divisibility by 4 because if 2 doesn’t divide into 107, then no multiple of 2 can divide into it. Is 107 divisible by 5? The last digit is a 7 so, no. We don’t need to check for divisibility by 6 because if 2 doesn’t divide into 107, then no multiple of 2 can divide into it. 25 of 53 © Boardworks Ltd 2004

Testing for prime numbers Is 107 a prime number? We can check whether or not a number is prime by testing for divisibility by successive numbers. Is 107 divisible by 7? Dividing by 7 leaves a remainder so no. We don’t need to check for divisibility by 8 because if 2 doesn’t divide into 107, then no multiple of 2 can divide into it. We don’t need to check for divisibility by 9 because if 3 doesn’t divide into 107, then no multiple of 2 can divide into it. We don’t need to check for divisibility by 10 because if 2 doesn’t divide into 107, then no multiple of 2 can divide into it. 26 of 53 © Boardworks Ltd 2004

Testing for prime numbers Is 107 a prime number? We can check whether or not a number is prime by testing for divisibility by successive prime numbers. We don’t Why don’tneed we need to check for divisibility by 11 bybecause 11? we have found that no number below 10 divides into 107. That means that any number that multiplied 11 would have to be bigger than 10. Since, 10 × 11 is bigger than 107 we can stop here. 107 is a prime number. 27 of 53 © Boardworks Ltd 2004

Testing for prime numbers When we are testing whether or not a number is prime, we only have to test for divisibility by prime numbers. We don’t need to check for divisibility by any number bigger than the square root of the number. A number is prime if no prime number less than the square root of the number divides into it. Also, all prime numbers greater than 5 must end in a 1, 3, 7 or 9. 28 of 53 © Boardworks Ltd 2004

An amazing fact 29 of 53 © Boardworks Ltd 2004

Contents N 3 Multiples, factors and primes N 3. 1 Divisibility N 3. 2 Multiples and factors N 3. 3 Prime numbers N 3. 4 Prime factor decomposition N 3. 5 HCF and LCM 30 of 53 © Boardworks Ltd 2004

Prime factors A prime factor is a factor that is a prime number. For example, What are the factors of 30? The factors of 30 are: 1 2 3 5 6 10 15 30 The prime factors of 30 are 2, 3, and 5. 31 of 53 © Boardworks Ltd 2004

Products of prime factors 2 × 3 × 5 = 30 2 × 2 × 7 = 56 This can be written as 23 × 7 = 56 3 × 11 = 99 This can be written as 32 × 11 = 99 Every whole number greater than 1 is either a prime number or can be written as a product of two or more prime numbers. 32 of 53 © Boardworks Ltd 2004

The prime factor decomposition When we write a number as a product of prime factors it is called the prime factor decomposition. For example, The prime factor decomposition of 100 is: 100 = 2 × 5 × 5 = 2 2 × 52 There are 2 methods of finding the prime factor decomposition of a number. 33 of 53 © Boardworks Ltd 2004

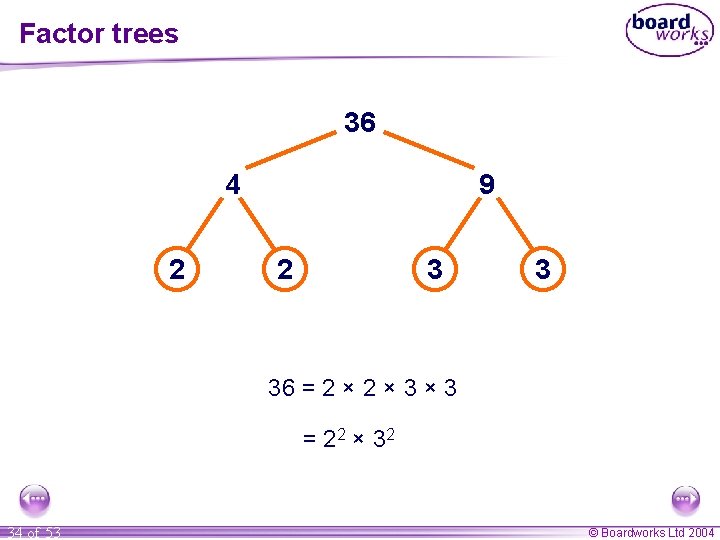
Factor trees 36 4 2 9 2 3 3 36 = 2 × 3 × 3 = 2 2 × 32 34 of 53 © Boardworks Ltd 2004

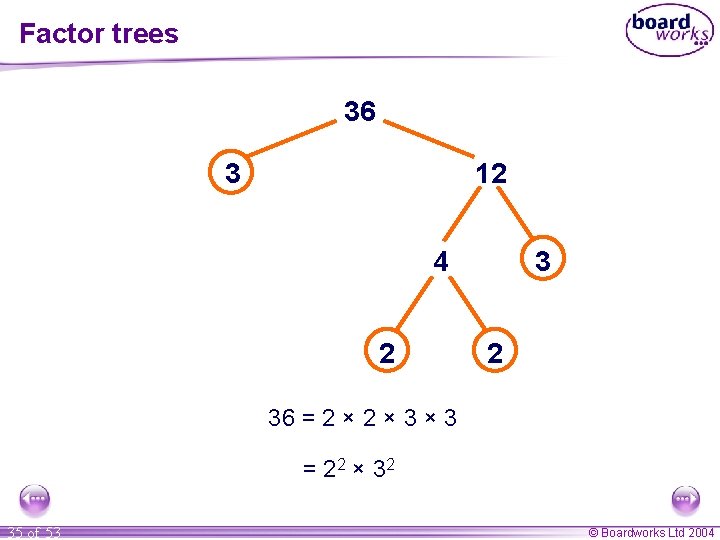
Factor trees 36 3 12 4 2 36 = 2 × 3 × 3 = 2 2 × 32 35 of 53 © Boardworks Ltd 2004

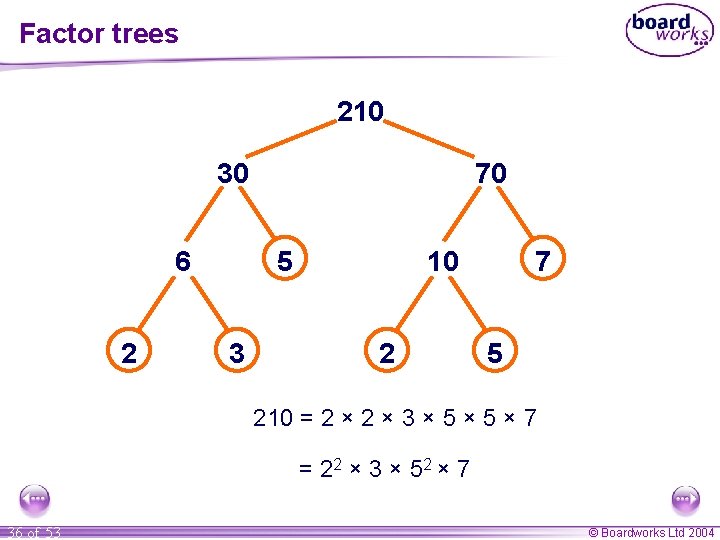
Factor trees 210 30 6 2 70 5 3 10 2 7 5 210 = 2 × 3 × 5 × 7 = 2 2 × 3 × 52 × 7 36 of 53 © Boardworks Ltd 2004

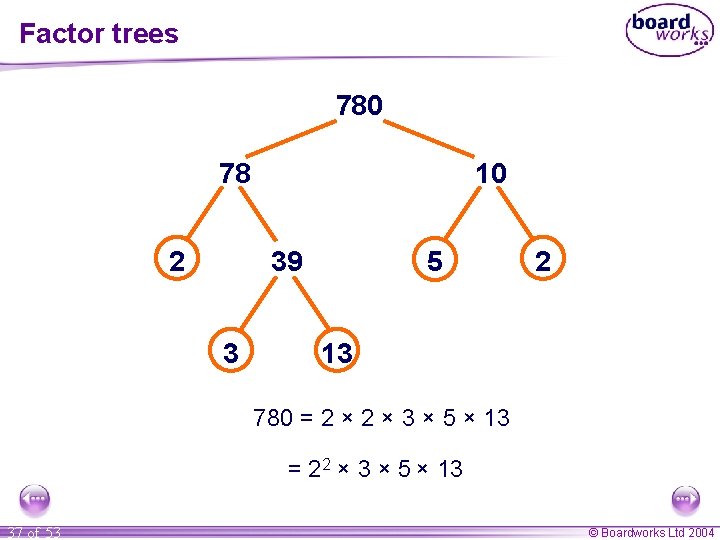
Factor trees 780 78 2 10 39 3 5 2 13 780 = 2 × 3 × 5 × 13 = 22 × 3 × 5 × 13 37 of 53 © Boardworks Ltd 2004

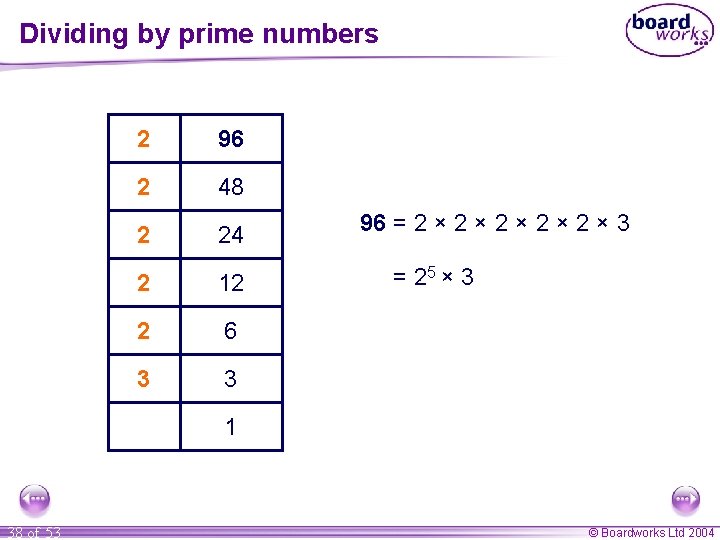
Dividing by prime numbers 2 96 2 48 2 24 2 12 2 6 3 3 96 = 2 × 2 × 2 × 3 = 25 × 3 1 38 of 53 © Boardworks Ltd 2004

Dividing by prime numbers 3 315 3 105 315 = 3 × 5 × 7 5 35 = 32 × 5 × 7 7 7 1 39 of 53 © Boardworks Ltd 2004

Dividing by prime numbers 2 702 3 351 3 117 3 39 13 13 702 = 2 × 3 × 3 × 13 = 2 × 33 × 13 1 40 of 53 © Boardworks Ltd 2004

Contents N 3 Multiples, factors and primes N 3. 1 Divisibility N 3. 2 Multiples and factors N 3. 3 Prime numbers N 3. 4 Prime factor decomposition N 3. 5 HCF and LCM 41 of 53 © Boardworks Ltd 2004

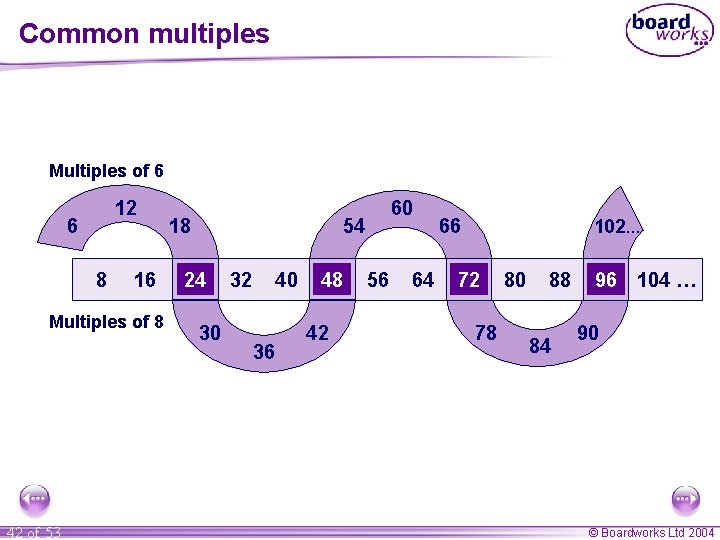
Common multiples Multiples of 6 12 6 8 16 Multiples of 8 42 of 53 18 60 54 24 30 32 40 36 48 42 56 64 66 102… 72 78 80 88 84 96 104 … 90 © Boardworks Ltd 2004

Multiples on a hundred grid 43 of 53 © Boardworks Ltd 2004

The lowest common multiple (or LCM) of two numbers is the smallest number that is a multiple of both the numbers. We can find this by writing down the first few multiples for both numbers until we find a number that is in both lists. For example, Multiples of 20 are : 20, 40, 60, 80, 100, Multiples of 25 are : 25, 50, 75, 100, 125, . . . 120, . . . The LCM of 20 and 25 is 100. 44 of 53 © Boardworks Ltd 2004

The lowest common multiple What is the lowest common multiple (LCM) of 8 and 10? The first ten multiples of 8 are: 8 16 24 32 40 48 56 64 70 80 72 80 … 100 … The first ten multiples of 10 are: 10 20 30 40 50 60 90 The lowest common multiple (LCM) of 8 and 10 is 40 The lowest common multiple (LCM) of two numbers is the smallest number that is a multiple of both. 45 of 53 © Boardworks Ltd 2004

The lowest common multiple We use the lowest common multiple when adding and subtracting fractions. For example, Add together 4 9 and 5 12 The LCM of 9 and 12 is 36. 4 9 + × 4 × 3 5 16 12 × 4 46 of 53 = 36 + 15 36 = 31 36 × 3 © Boardworks Ltd 2004

Common factor diagram 47 of 53 © Boardworks Ltd 2004

The highest common factor (or HCF) of two numbers is the highest number that is a factor of both numbers. We can find the highest common factor of two numbers by writing down all their factors and finding the largest factor in both lists. For example, Factors of 36 are : 1, 2, 3, 4, 6, Factors of 45 are : 1, 3, 5, 9, 12, 18, 36. 45. The HCF of 36 and 45 is 9. 48 of 53 © Boardworks Ltd 2004

The highest common factor What is the highest common factor (HCF) of 24 and 30? The factors of 24 are: 1 2 3 4 6 8 12 24 10 15 30 The factors of 30 are: 1 2 3 5 6 The highest common factor (HCF) of 24 and 30 is 6 The highest common factor (HCF) of two numbers is the highest whole number which divides into both. 49 of 53 © Boardworks Ltd 2004

The highest common factor We use the highest common factor when cancelling fractions. For example, Cancel the fraction 36 48 The HCF of 36 and 48 is 12, so we need to divide the numerator and the denominator by 12. ÷ 12 36 48 = 3 4 ÷ 12 50 of 53 © Boardworks Ltd 2004

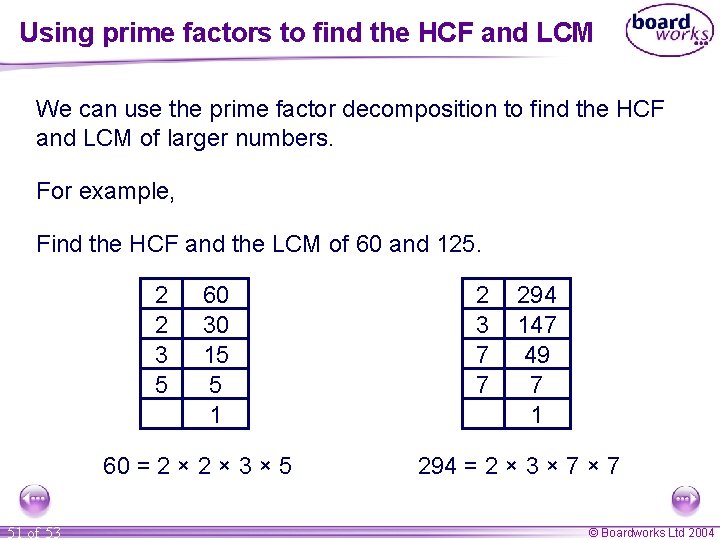
Using prime factors to find the HCF and LCM We can use the prime factor decomposition to find the HCF and LCM of larger numbers. For example, Find the HCF and the LCM of 60 and 125. 2 2 3 5 60 30 15 5 1 60 = 2 × 3 × 5 51 of 53 2 3 7 7 294 147 49 7 1 294 = 2 × 3 × 7 © Boardworks Ltd 2004

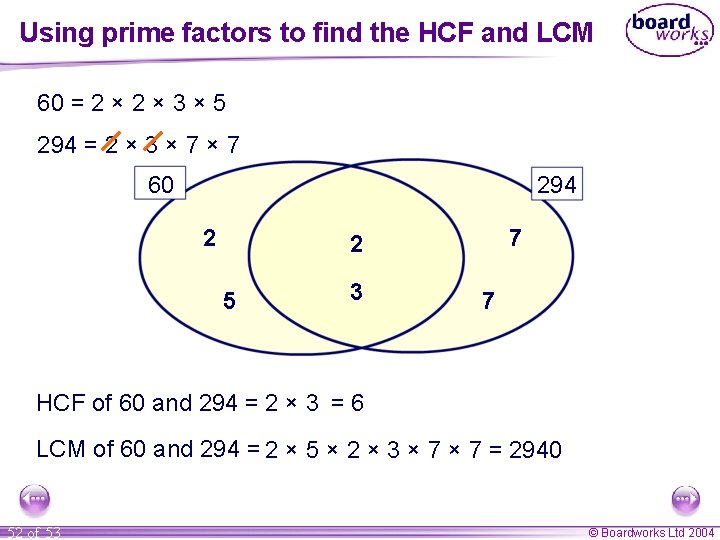
Using prime factors to find the HCF and LCM 60 = 2 × 3 × 5 294 = 2 × 3 × 7 60 294 2 7 2 5 3 7 HCF of 60 and 294 = 2 × 3 = 6 LCM of 60 and 294 = 2 × 5 × 2 × 3 × 7 = 2940 52 of 53 © Boardworks Ltd 2004

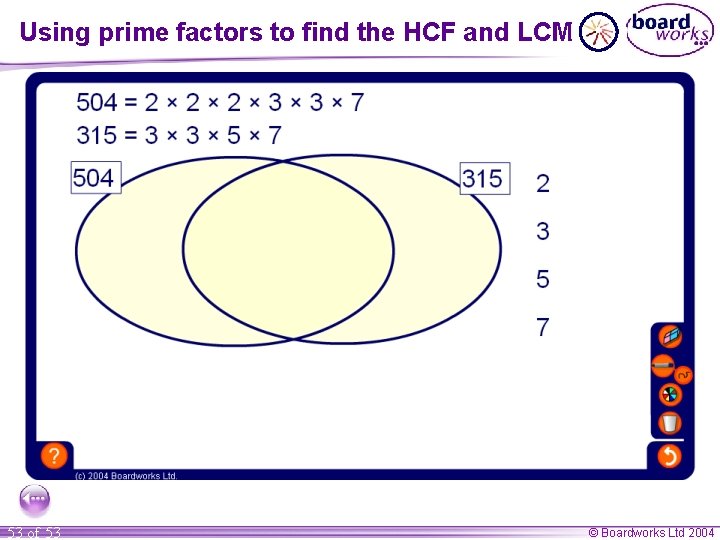
Using prime factors to find the HCF and LCM 53 of 53 © Boardworks Ltd 2004