MULTIPLES AND FACTORS LESSON 1 WHAT ARE MULTIPLES












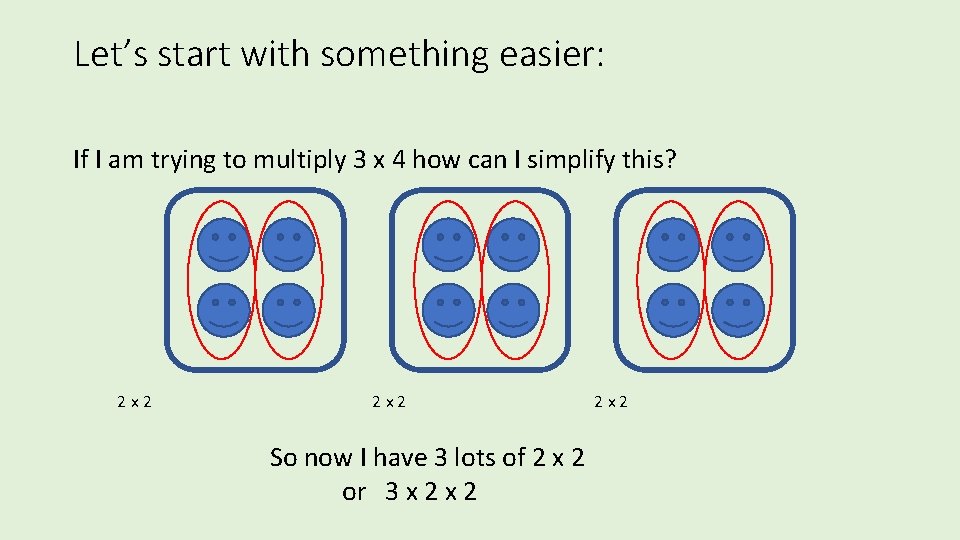









- Slides: 30

MULTIPLES AND FACTORS LESSON 1

WHAT ARE MULTIPLES? Multiples are numbers that a number can be multiplied into by a whole number. In other words, they are the answers to the times tables for a number.

Multiples can be depicted in diagrams: 1 group of 2 1 x 2 = 2 2 and 4 are multiples of 2 2 groups of 2 2 x 2 = 4

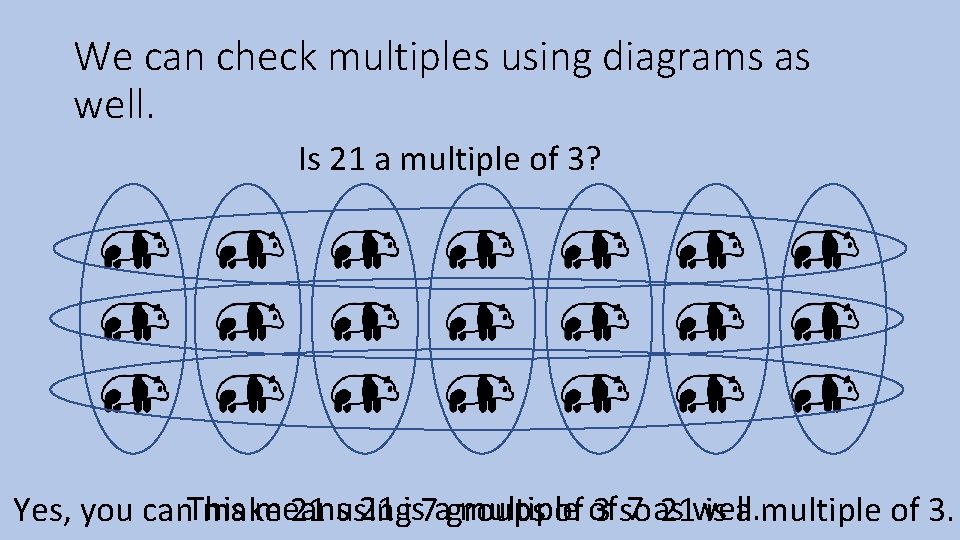
We can check multiples using diagrams as well. Is 21 a multiple of 3? This means 21 is a multiple of 7 as well. Yes, you can make 21 using 7 groups of 3 so 21 is a multiple of 3.

Multiples of 2 First I want to count in 2 s to find the multiples of 2. Yes, definitely a pattern. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 I’ve spotted a pattern but I’ll keep going until I finish my 2 times-tables. These are all the multiples of 2 up to 100. I notice they are all even numbers.

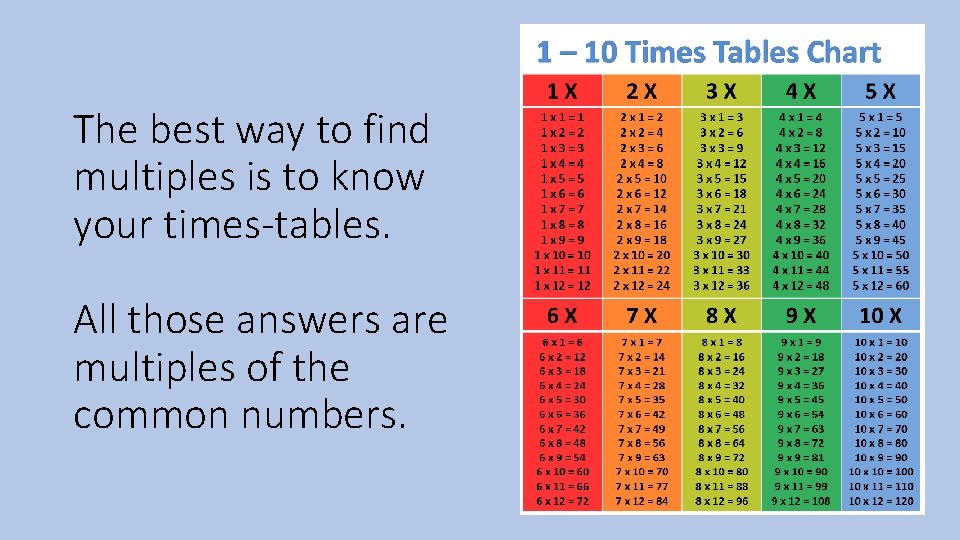
The best way to find multiples is to know your times-tables. All those answers are multiples of the common numbers.

What are factors? Factors are the opposite to multiples. A factor is what you get when you divide a larger number by a whole number. In other words, a umber that will fit into a larger number by an exact amount. So 5 is a factor of 10 because 5 x 2 = 10. 2 is also a factor of 10 because 2 x 5 = 10. Can you think of other factors of 10? 1 x 10 = 10 so 1 and 10 are factors of 10

Factors normally work in pairs Arrays are a great way of finding factor pairs, where the height and width of the array are both factors of a number. Lets look for factors of 12: 12 1 Factor pairs of 12 6 2 4 3 1 and 12 are factors of 12 1 12 2 6 3 4 2 and 6 are factors of 12 3 and 4 are factors of 12

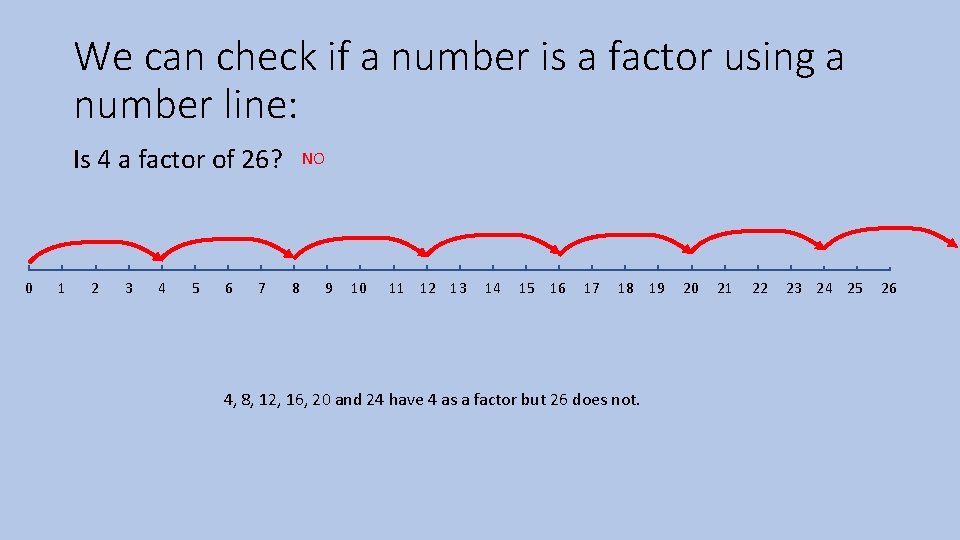
We can check if a number is a factor using a number line: Is 4 a factor of 26? NO 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 4, 8, 12, 16, 20 and 24 have 4 as a factor but 26 does not.

The best way to find factors is to know your times-tables. All those multiplications are factors of the answers.

PRIME NUMBERS AND USING FACTORS LESSON 2

WHAT IS A PRIME NUMBER? A prime number is a number what only has itself and 1 as factors. For example 3: 3 1 Factors of 3 are 1 and 3 but no other number can be made a factor of 3. 3 is a PRIME NUMBER.

Lowest Prime Number 1 is not a prime number because a Prime Number MUST have 2 factors; 1 and itself. 1 only has the factor “ 1”. So the lowest Prime Number is… 2 2 1

How can we prove if a number is prime? First, how can we eliminate half of all the numbers? 4, 6, 8, 10, 12, 14, 16, 18, 20 All these numbers are even and are, therefore, multiples of 2 so not prime. What other times tables rules could we check? 5. a r o a 0 h t i w d en ays w l a of 5 es ipl t l u M All multip les of 10 e nd in a 0. If you add u p the digits of the num and it equa ber ls 9 it is a m ultiple of 9 e. g. 36 … 3. +6 = 9 so 3 6 is a multip le of 9 Multiples of 11 repeat a number. E. g. 3 x 11 = 33 or 66 = 11 x 6

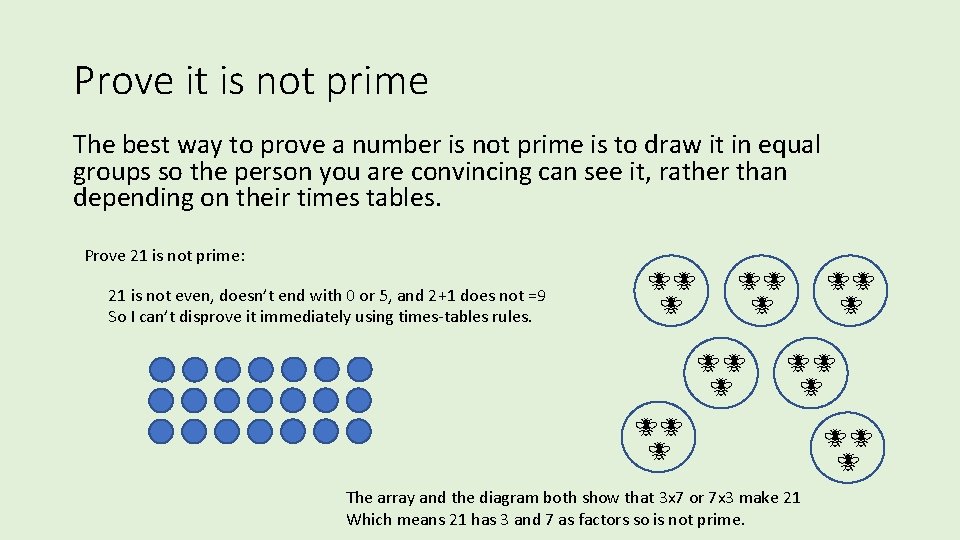
Prove it is not prime The best way to prove a number is not prime is to draw it in equal groups so the person you are convincing can see it, rather than depending on their times tables. Prove 21 is not prime: 21 is not even, doesn’t end with 0 or 5, and 2+1 does not =9 So I can’t disprove it immediately using times-tables rules. The array and the diagram both show that 3 x 7 or 7 x 3 make 21 Which means 21 has 3 and 7 as factors so is not prime.

Using Factors We can use factors to help with larger multiplications. 3 x 18 = ?
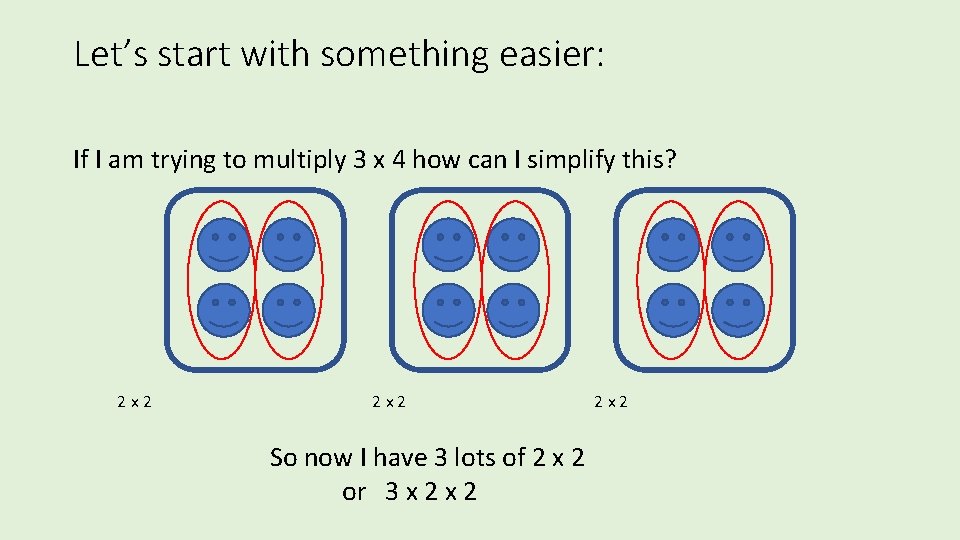
Let’s start with something easier: If I am trying to multiply 3 x 4 how can I simplify this? 2 x 2 So now I have 3 lots of 2 x 2 or 3 x 2 2 x 2

15 x 3 = ? First I want to try and convert the numbers into factors I feel more confident working with. 15 5 x 3 So now I have: 5 x 3 I can do 3 x 3 first because multiplying by 5 is easier. 3 x 3 = 9 so now I have 5 x 9 15 x 3 = 5 x 9 = 45 ? 45

Prime Factors are factors which are prime numbers. Prime Factor Trees We can split a number down to its prime factors to help with our calculations: Let’s find the prime factors of: 50 As 50 is even, let’s start by halving it: 50 = 2 x 5 2 x 25 As 25 ends in 5, we know it has 5 as a factor: 5 x 5

SQUARES AND CUBES LESSON 3

Squares and Square numbers that have a factor that Squares have all equal sides which we can use to calculate area. multiplies by itself to make the number. 3 cm 3 3 3 cm 3 x 3 = 9 9 is a square number.

Square numbers 2 x 2 3 x 3 4 x 4 5 x 5 6 x 6 7 x 7 etc All of these answers are square numbers, because the arrays would be in square shapes. 2 x 2 3 x 3 4 x 4 5 x 5 Istead of writing the full calculation, we can use the quick method using the 2 symbol.

42 is not the same as 4 x 2 The 2 symbol means a number is being multiplied by itself. So the number appears twice in the multiplication. 42 = 4 x 4 So what calculation would 52 represent? 2 5 = 5 x 5

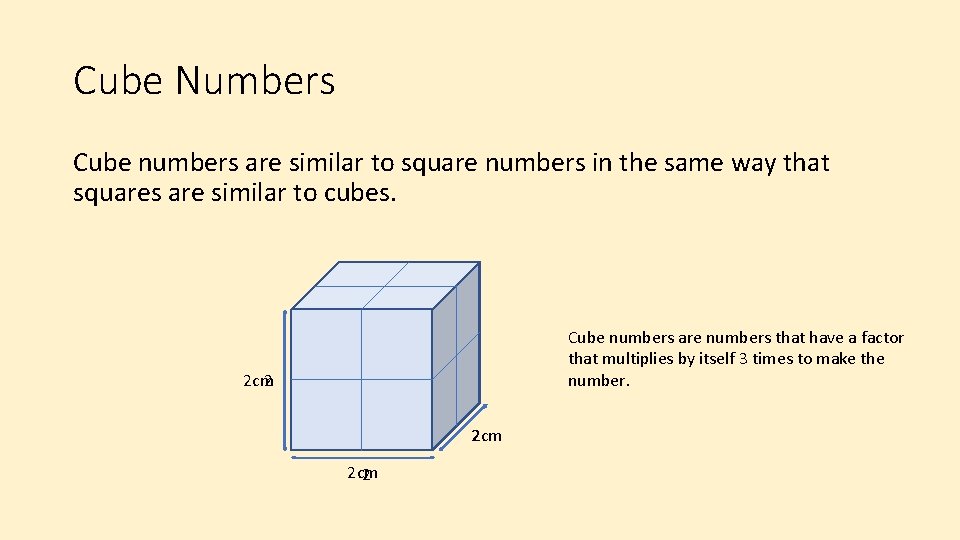
Cube Numbers Cube numbers are similar to square numbers in the same way that squares are similar to cubes. Cube numbers are numbers that have a factor that multiplies by itself 3 times to make the number. 2 cm 2 22 cm 2

23 is not 2 x 3 We use the symbol 3 to show a number is multiplying by itself 3 times. So the number appears 3 times in the multiplication. 23 = 2 x 2 So what calculation would 43 represent? 43 = 4 x 4

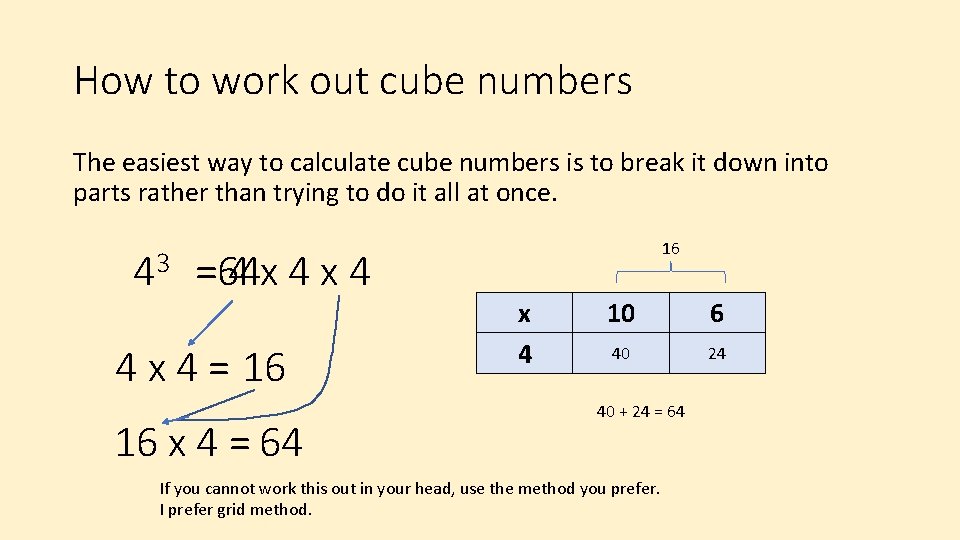
How to work out cube numbers The easiest way to calculate cube numbers is to break it down into parts rather than trying to do it all at once. =4 x 4 x 4 43 =64 4 x 4 = 16 16 x 4 = 64 16 x 4 10 6 40 24 40 + 24 = 64 If you cannot work this out in your head, use the method you prefer. I prefer grid method.

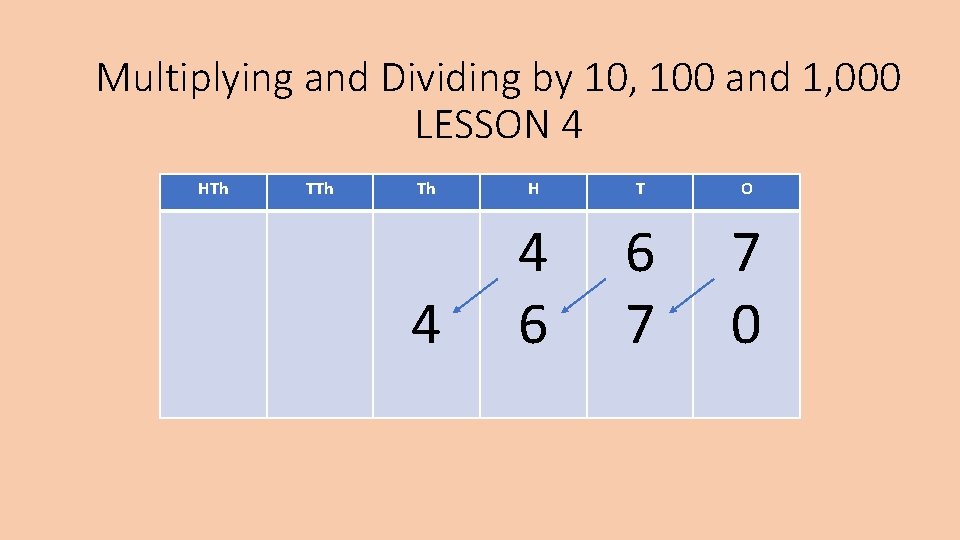
Multiplying and Dividing by 10, 100 and 1, 000 LESSON 4 HTh Th H T O 4 4 6 6 7 7 0

Multiplying by 10 When multiplying by 10 we must remember that each digit is being multiplied and we should think about place value. Let’s try with a bigger number: We can use a place Value Grid to show this. So 10 x 3 10 x 1 = 10 Ones = 1 Ten = 30 So 10 x 3 = 10 Ones x 3= 1 Ten x 3 = 3 Tens 473 x 10 = 4730 1 HTh 1 11 1 TTh 1 11 1 1 Th 1 1 1 When multiplying by 10 we slide the digits up one 1 1 column 11 1 H 1 1 4 T 7 3 1 When multiplying 1 by 10 we slide the digits up one column 1 1 4 7 1 1 1 O 3 = 0 10 10 10 We use a 0 to hold any place value We use a 0 to hold columns that do not any place value have a digit in. 10 columns that do not have a digit in.

Multiply by 100 or 1, 000 When multiplying by 1000 we must remember that 1000 = 100 x 10 = 10 x 10. When multiplying by 100 we must remember that 100 = 10 x 10. So we are repeating the process again but this time sliding 3 columns. . So we are repeating the process we have just seen but twice. 1, 000 x 302 = 302, 000 100 x 2 = Lets try something higher: 100 x 322 = 32200 HTh HTh TTh Th H H H TTT O O O 3 02 02 0 When we multiply by 1000 When we multiply by 100 we slide the digit up three we slide the digit up two columns 3 03 2 We put 0 s in place to hold place value columns

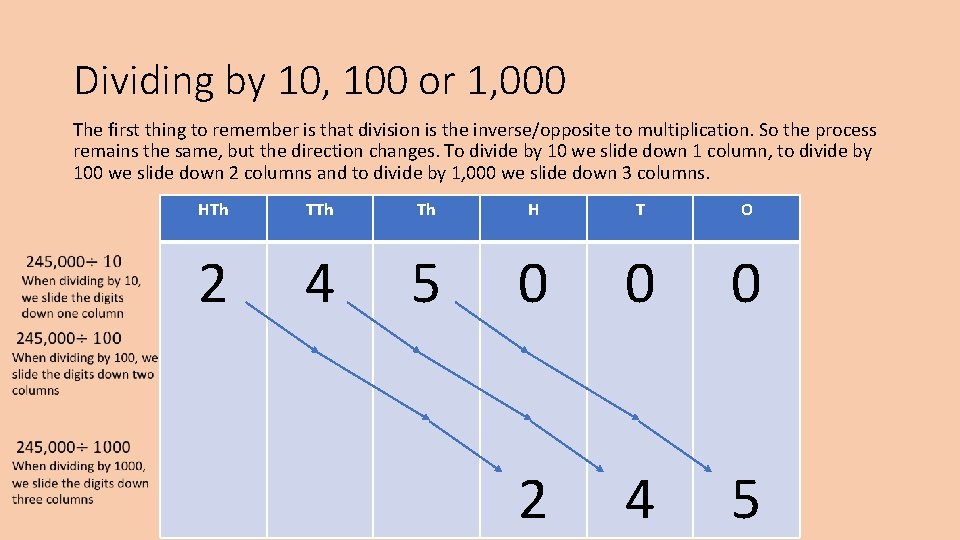
Dividing by 10, 100 or 1, 000 The first thing to remember is that division is the inverse/opposite to multiplication. So the process remains the same, but the direction changes. To divide by 10 we slide down 1 column, to divide by 100 we slide down 2 columns and to divide by 1, 000 we slide down 3 columns. HTh Th H T O 2 4 2 5 4 2 0 0 5 4 0 0 0 5