KS 4 Forces Speed and Acceleration Boardworks Ltd

KS 4 Forces – Speed and Acceleration © Boardworks Ltd 2003
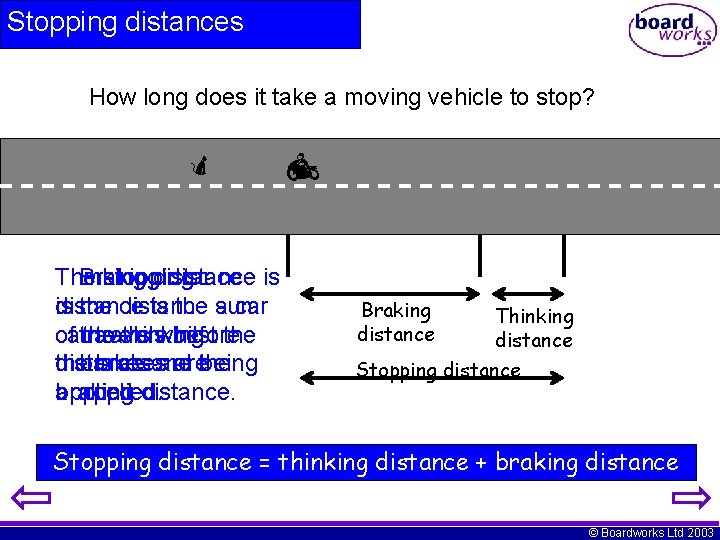
Stopping distances How long does it take a moving vehicle to stop? The Thinking Braking stopping distance is is the distance is the sum a cartravels of the travels thinking whilst before thebrakes distance brakes and arethe being applied. braking applied. distance. Braking distance Thinking distance Stopping distance = thinking distance + braking distance © Boardworks Ltd 2003
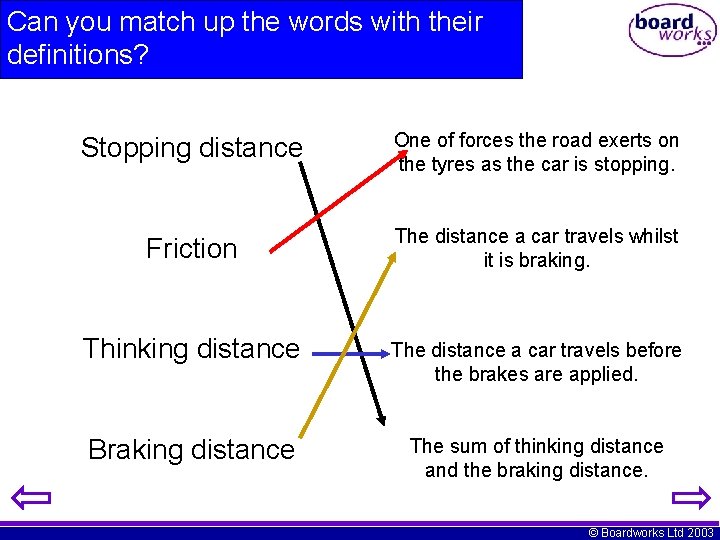
Can you match up the words with their definitions? Stopping distance One of forces the road exerts on the tyres as the car is stopping. Friction The distance a car travels whilst it is braking. Thinking distance The distance a car travels before the brakes are applied. Braking distance The sum of thinking distance and the braking distance. © Boardworks Ltd 2003
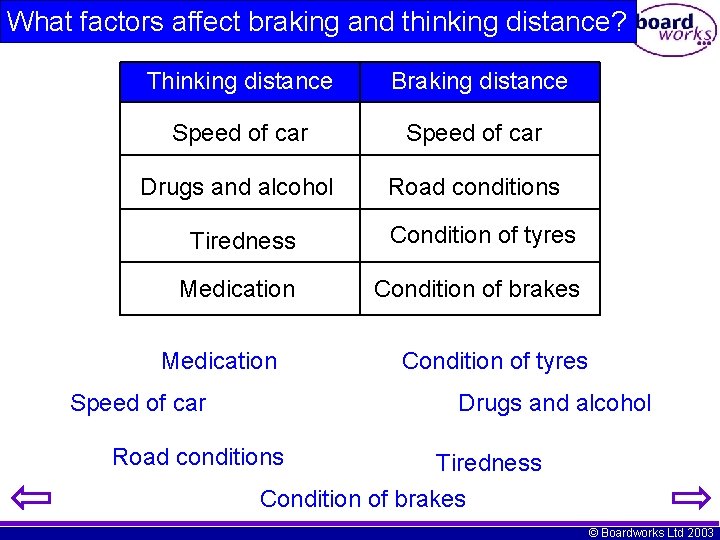
What factors affect braking and thinking distance? Thinking distance Braking distance Speed of car Drugs and alcohol Road conditions Tiredness Condition of tyres Medication Condition of brakes Medication Speed of car Condition of tyres Drugs and alcohol Road conditions Tiredness Condition of brakes © Boardworks Ltd 2003

Braking car question: A car is moving along an open road. Suddenly, a sheep walks into the road. a) What do we call the distance the car travels before the driver puts their foot on the brakes? Thinking distance b) Name one factor that could increase the distance the car travels in this time. Medication, drugs/alcohol, speed of car, tiredness c) The braking distance is 35 m for the car. If the stopping distance is 50 m, how far did the car travel before the driver put their foot on the brakes? Thinking distance = Stopping distance – braking distance = 50 m – 35 m = 15 m © Boardworks Ltd 2003

Car Graphing Activity This graphing experiment shows a movie of a car travelling along a straight road. Copy the results table shown on the next slide and complete it as the movie is played. Record the distance the car has travelled every five seconds. Then graph your results. Note that there are teacher’s notes, in “Notes View” on this slide. See teacher’s notes © Boardworks Ltd 2003
Results table for Distance / Time Graph Time/Seconds 0 5 10 Distance/Metres 15 20 25 30 35 40 45 50 55 © Boardworks Ltd 2003

© Boardworks Ltd 2003
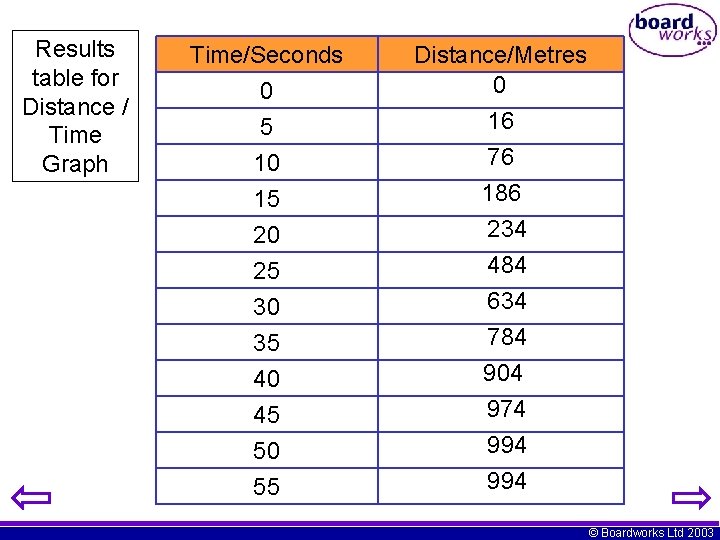
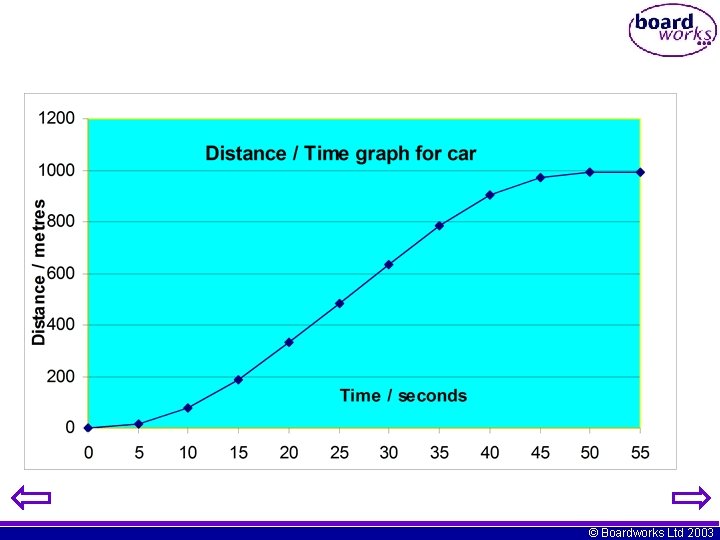
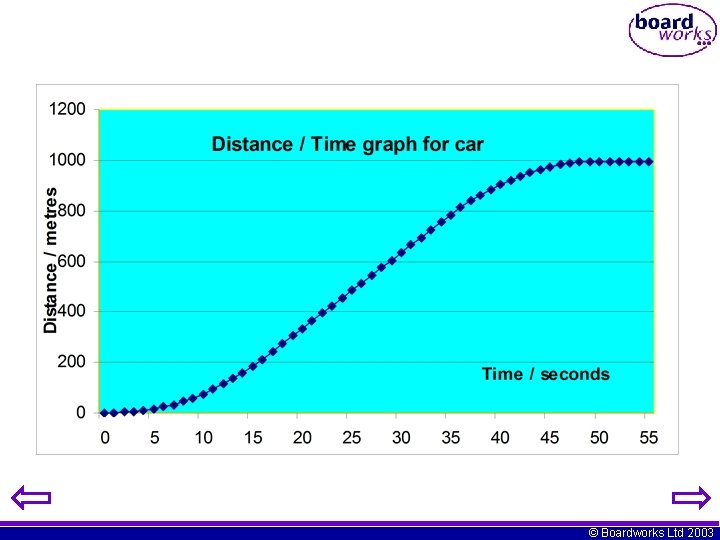
Results table for Distance / Time Graph Time/Seconds 0 5 10 15 20 25 30 35 40 45 50 55 Distance/Metres 0 16 76 186 234 484 634 784 904 974 994 © Boardworks Ltd 2003
© Boardworks Ltd 2003
© Boardworks Ltd 2003
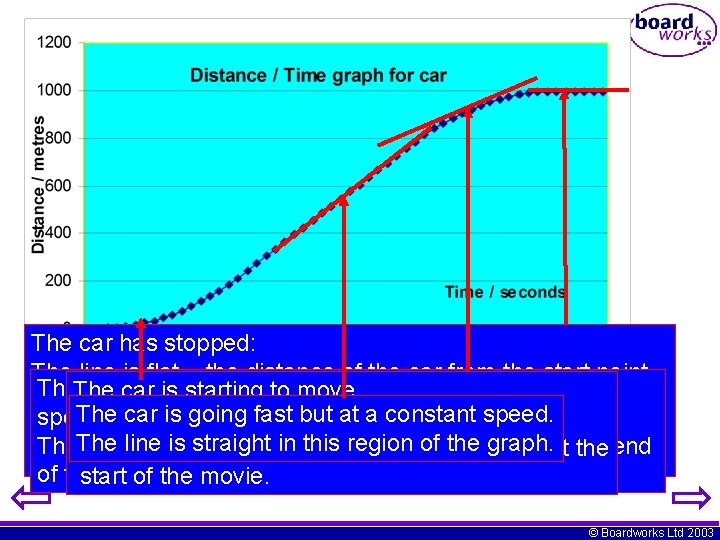
The car has stopped: The line is flat – the distance of the car from the start point The linecar on is thestarting graph to is not straight, so we know the move. is not changing. Theofcurve car going fast but atspeed a constant speed theiscar is changing. The shows that the is changing. The line is straight – meaning that there is no CHANGE in The lineisisdownwards straight in as this region of the down graph. at The curve the car slows curve is upwards as the car accelerates at the end speed. of the movie. start of the movie. © Boardworks Ltd 2003

Gradient of a Distance / Time Graph The speed of the car can be calculated by looking at the gradient of the Distance / Time graph. Speed is “Distance Travelled divided by Time Taken” Both these values can be read off the Distance / Time graph, and this is the same as the gradient of the line. © Boardworks Ltd 2003
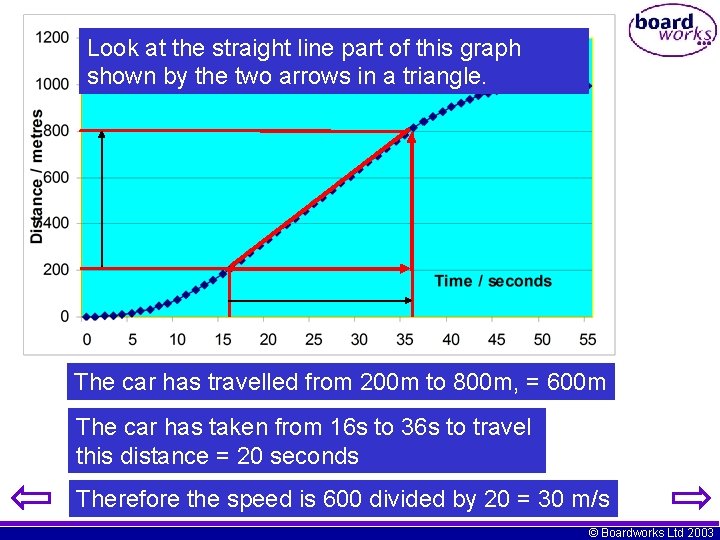
Look at the straight line part of this graph shown by the two arrows in a triangle. The car has travelled from 200 m to 800 m, = 600 m The car has taken from 16 s to 36 s to travel this distance = 20 seconds Therefore the speed is 600 divided by 20 = 30 m/s © Boardworks Ltd 2003

Plotting the Speed / Time Graph Having looked at the distance-time graph, plot the speed-time graph. Copy the results table shown on the next slide and complete it as the movie is played. Record the speed of the car at five second intervals. Then graph your results. © Boardworks Ltd 2003
Results table for Speed / Time Graph Time/Seconds 0 5 10 Speed/m/s 15 20 25 30 35 40 45 50 55 © Boardworks Ltd 2003
© Boardworks Ltd 2003
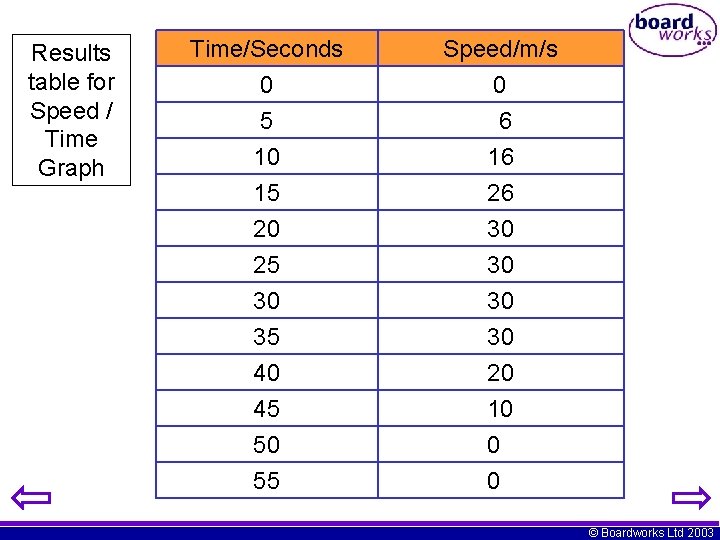
Results table for Speed / Time Graph Time/Seconds 0 5 10 15 20 25 30 35 40 45 50 55 Speed/m/s 0 6 16 26 30 30 20 10 0 0 © Boardworks Ltd 2003
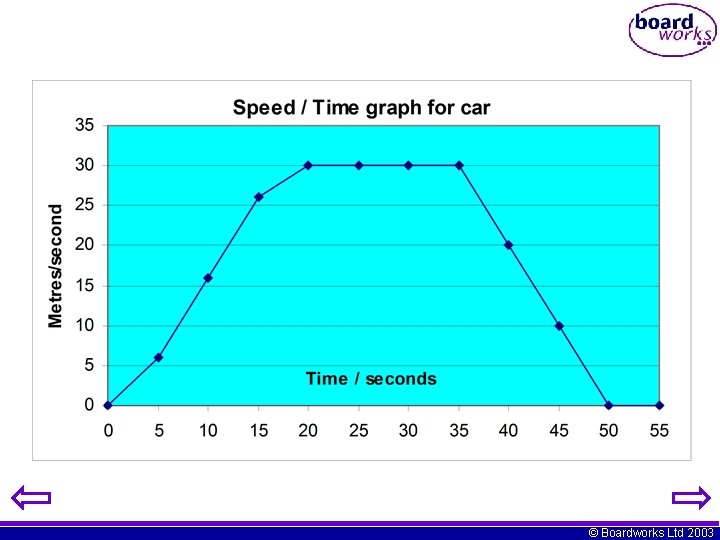
© Boardworks Ltd 2003
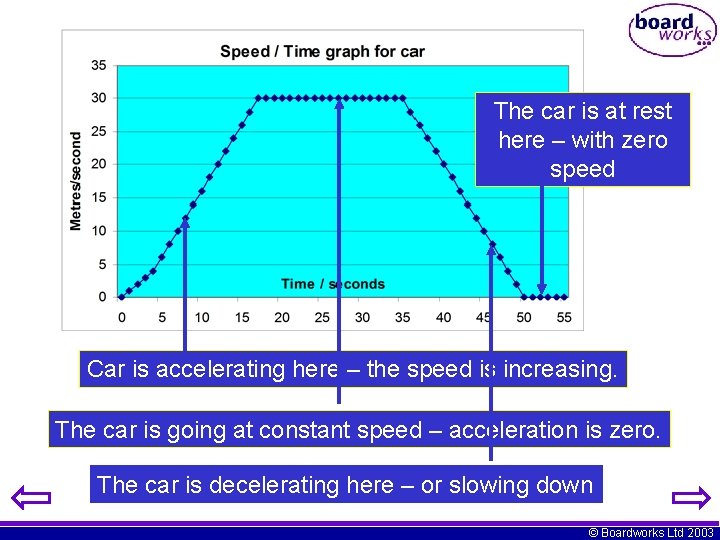
The car is at rest here – with zero speed Car is accelerating here – the speed is increasing. The car is going at constant speed – acceleration is zero. The car is decelerating here – or slowing down © Boardworks Ltd 2003
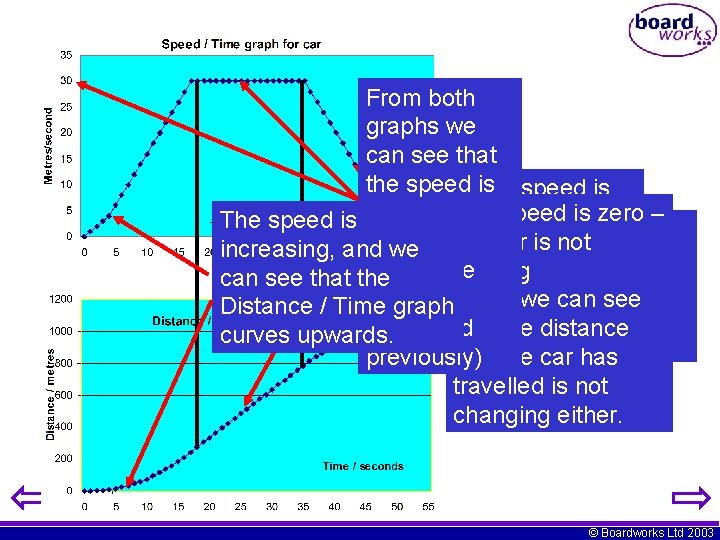
From both graphs we can see that the speed The is speed is and zero – decreasing The speed is 30 m/s. The Now compare the car is not the curve is increasing, and we Speed / Time graph (Using the moving downwards can see that the with the earlier value and we can see Distance / Time graph–Distance / Time calculated that the distance curves upwards. graph previously) that the car has travelled is not changing either. © Boardworks Ltd 2003

S=d/t We can express the speed formula using the equation: Speed = Distance ÷ Time S =d/t Speed measured in metres per second (m/s) Distance measured in metres (m) Time measured in seconds (s) © Boardworks Ltd 2003
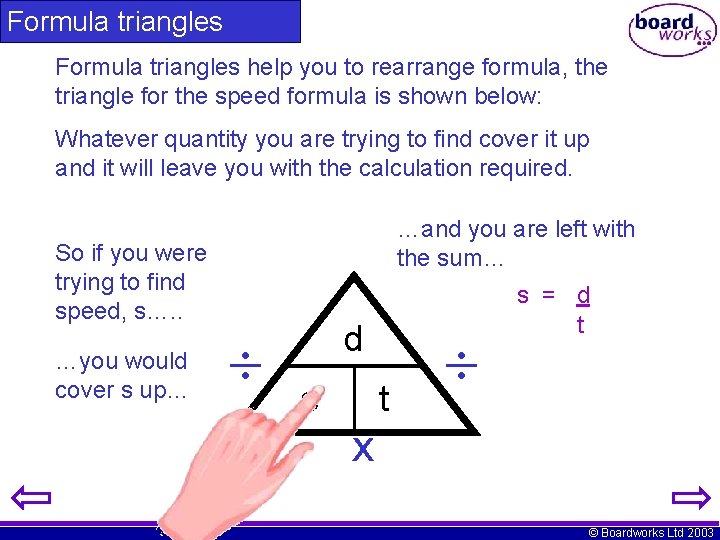
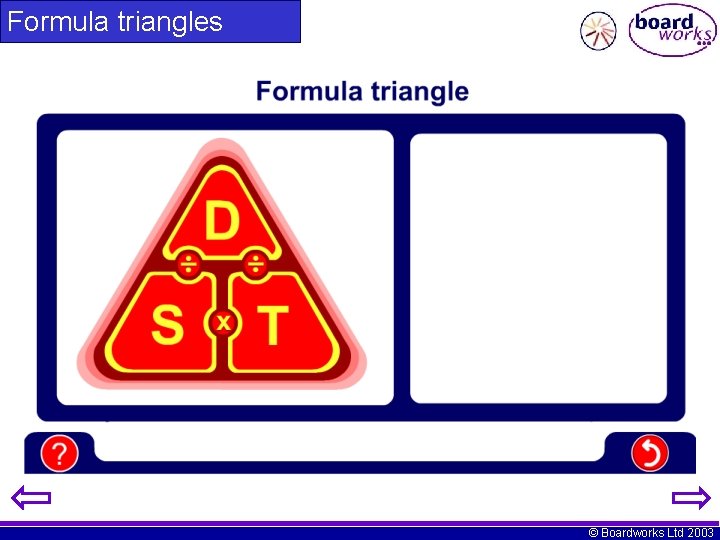
Formula triangles help you to rearrange formula, the triangle for the speed formula is shown below: Whatever quantity you are trying to find cover it up and it will leave you with the calculation required. So if you were trying to find speed, s…. . …you would cover s up… …and you are left with the sum… d s t s = d t x © Boardworks Ltd 2003
Formula triangles © Boardworks Ltd 2003
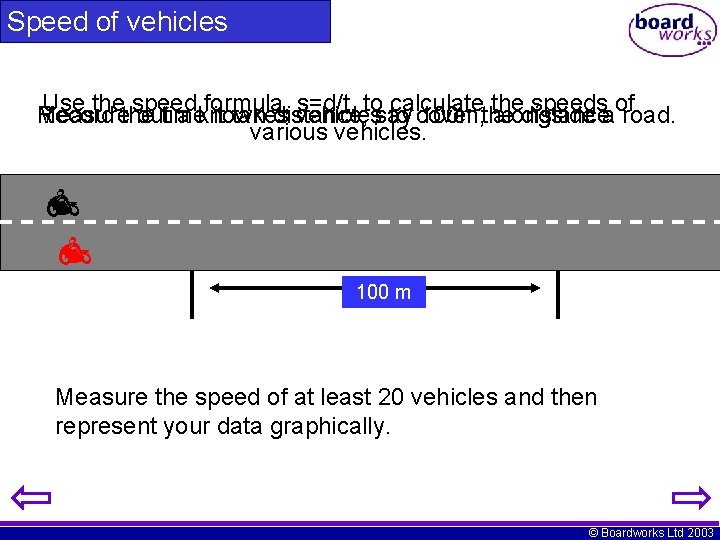
Speed of vehicles Use thethe speed formula, s=d/t, tosay calculate the speedsaof Measure Record outtime a known it takes distance, vehicles to cover 100 m, the alongside distance. road. various vehicles. 100 m Measure the speed of at least 20 vehicles and then represent your data graphically. © Boardworks Ltd 2003
- Slides: 25