Review of Factoring Techniques Factoring Factoring is a










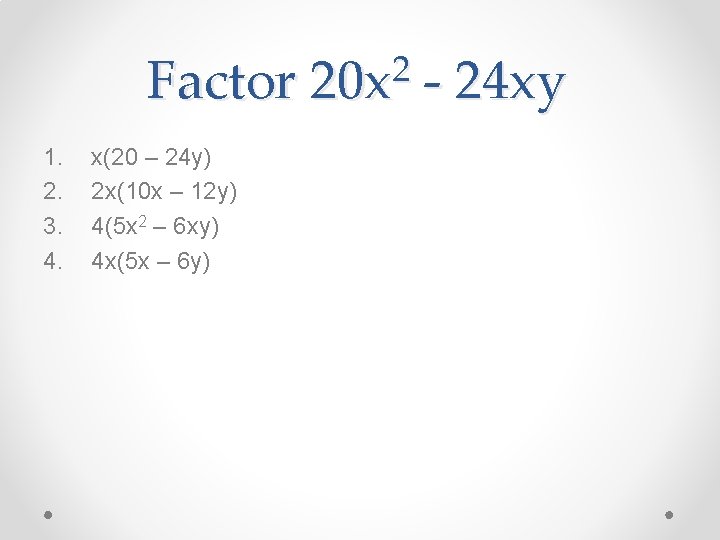

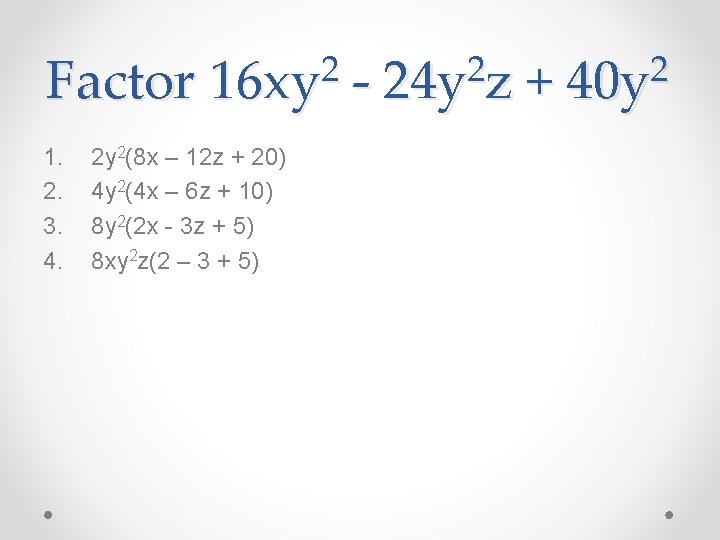




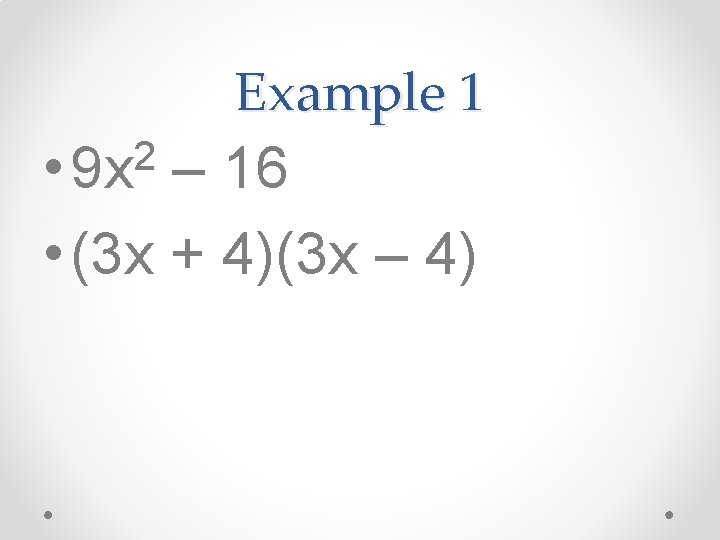

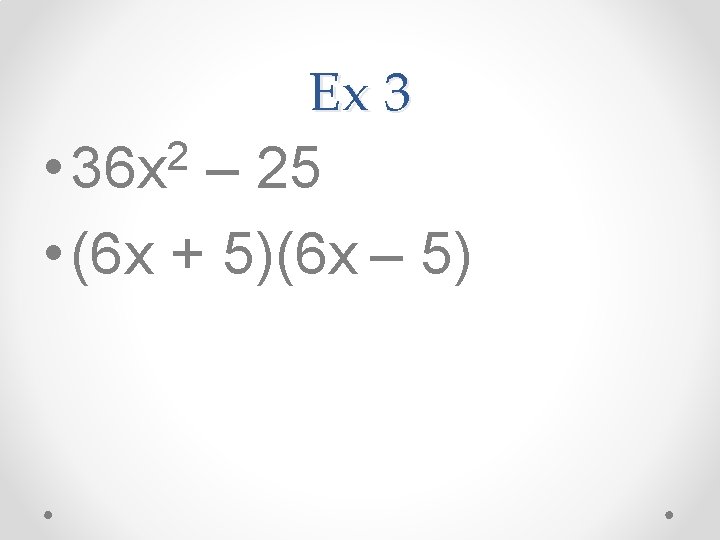
















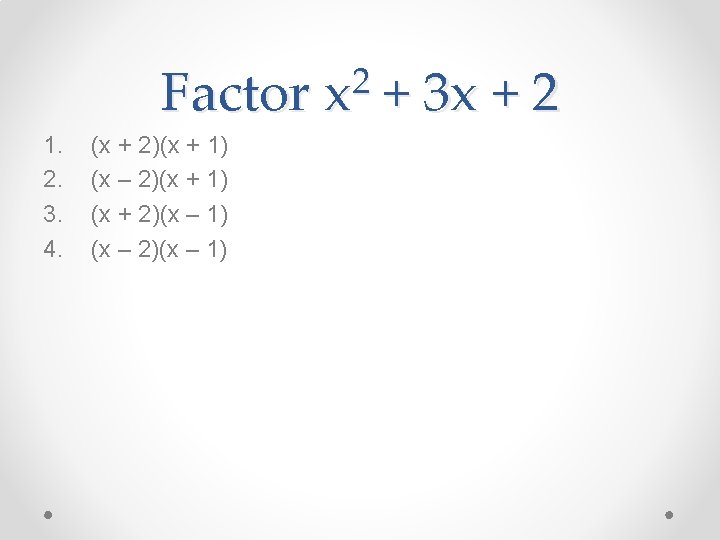


- Slides: 39

Review of Factoring Techniques

Factoring? • Factoring is a method to find the basic numbers and variables that made up a product. • (Factor) x (Factor) = Product • Some numbers are Prime, meaning they are only divisible by themselves and 1 and not factorable.

When factoring trinomials, we always try GCF method first!!!! Number of terms Factoring Technique 2 Difference of 2 Squares 3 Sum and Product Method 4 or 6 Grouping

GCF Method

Warm-UP - Distribute each problem:

GCF Method is just distributing backwards!!

Greatest Common Factors aka GCF’s Factor out the GCF for each polynomial: Factor out means you need the GCF times the remaining parts. a) b) c) d) e) 2 x + 4 y 5 a – 5 b 18 x – 6 y 2 m + 6 mn 5 x 2 y – 10 xy 2(x + 2 y) 5(a – b) How can you check? 6(3 x – y) 2 m(1 + 3 n) 5 xy(x - 2)

Review: What is the GCF of 25 a 2 and 15 a? 5 a Let’s go one step further… 1) FACTOR 25 a 2 + 15 a. Find the GCF and divide each term 25 a 2 + 15 a = 5 a( ___ + ___ ) 5 a 3 Check your answer by distributing.

2) Factor 2 18 x - 3 12 x. Find the GCF 6 x 2 Divide each term by the GCF 18 x 2 - 12 x 3 = 6 x 2( ___ ) 3 2 x Check your answer by distributing.

3) Factor 2 28 a b + 2 56 abc. GCF = 28 ab Divide each term by the GCF 28 a 2 b + 56 abc 2 = 28 ab ( ___ + ___ )2 a 2 c Check your answer by distributing. 28 ab(a + 2 c 2)
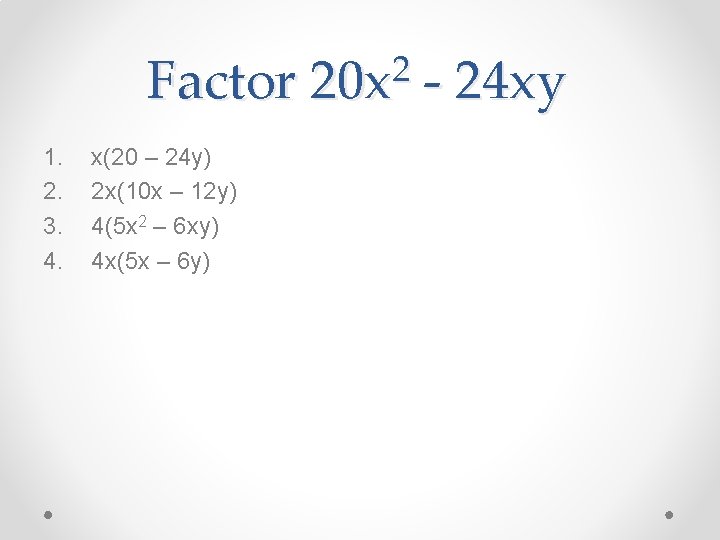
Factor 1. 2. 3. 4. x(20 – 24 y) 2 x(10 x – 12 y) 4(5 x 2 – 6 xy) 4 x(5 x – 6 y) 2 20 x - 24 xy

5) Factor 2 28 a + 21 b - 2 2 35 b c GCF = 7 Divide each term by the GCF 4 a 2 + ___ 3 b - ____ 5 b 2 c 2 ) 28 a 2 + 21 b - 35 b 2 c 2 = 7 ( ___ Check your answer by distributing. 7(4 a 2 + 3 b – 5 b 2 c 2)
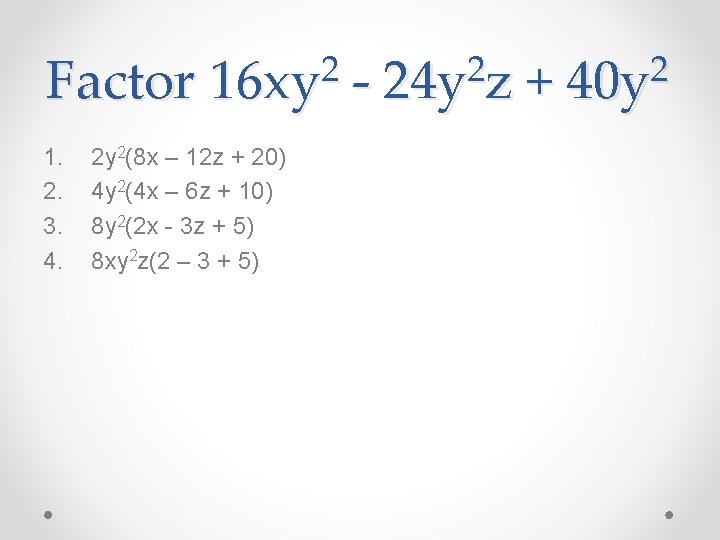
Factor 1. 2. 3. 4. 2 16 xy 2 y 2(8 x – 12 z + 20) 4 y 2(4 x – 6 z + 10) 8 y 2(2 x - 3 z + 5) 8 xy 2 z(2 – 3 + 5) - 2 24 y z + 2 40 y

Method #2 • Difference of Two Squares 2 2 • a – b = (a + b)(a - b)

What is a Perfect Square • Any term you can take the square root evenly (No decimal) • 25 • 36 • 1 • x 2 • y 4

Difference of Perfect Squares 2 x – 4 = the answer will look like this: ( )( take the square root of each part: ( x 2)(x 2) Make 1 a plus and 1 a minus: (x + 2)(x - 2 ) )

FACTORING Difference of Perfect Squares EX: x 2 – 64 How: Solution: Take the square root of (x – 8)(x + 8) each part. One gets a + and one gets a -. Check answer by FOIL.
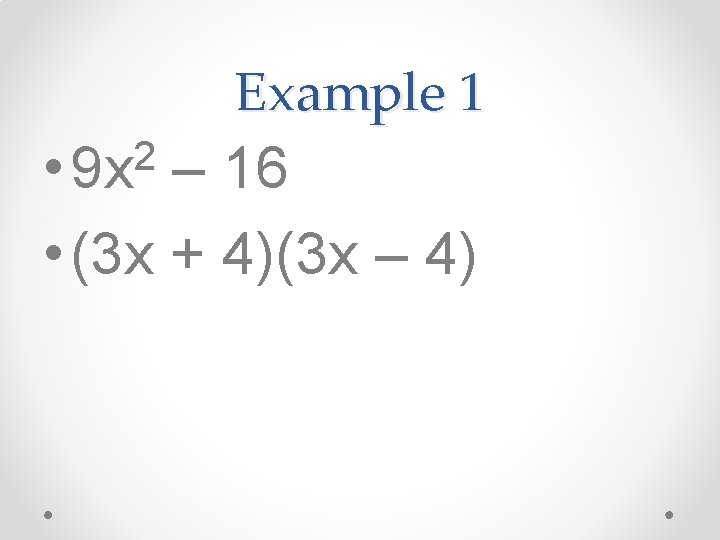
Example 1 2 • 9 x – 16 • (3 x + 4)(3 x – 4)

Example 2 2 • x – 16 • (x + 4)(x – 4)
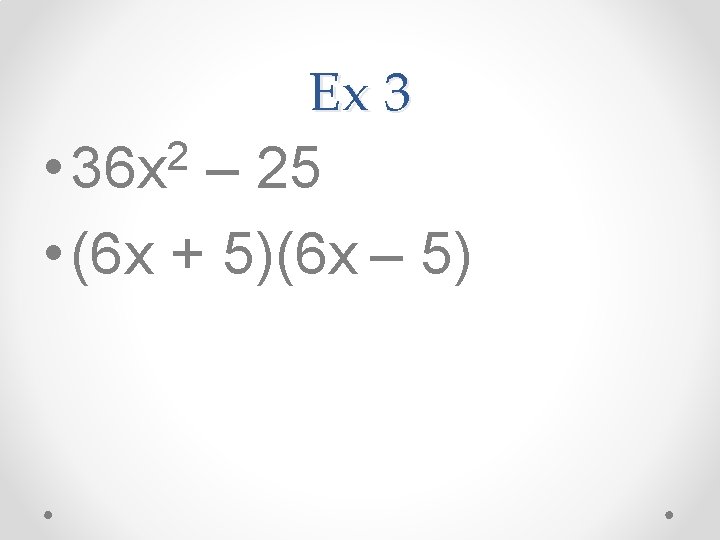
Ex 3 2 • 36 x – 25 • (6 x + 5)(6 x – 5)

More than ONE Method • It is very possible to use more than one factoring method in a problem • Remember: • ALWAYS use GCF first

Example 1 • – 50 x • GCF = 2 x 2 • 2 x(b – 25) • 2 nd term is the diff of 2 squares • 2 x(b + 5)(b - 5) 2 2 b x

Example 2 • • • 32 x 3 – 2 x GCF = 2 x 2 x(16 x 2 – 1) 2 nd term is the diff of 2 squares 2 x(4 x + 1)(4 x - 1)

ax 2 + bx + c

Example 1: x 2 + 11 x + 24 When factoring these trinomials the factors will be two binomials: (x + ) We know that the first terms of each binomial must be x because the first term of the trinomial is x 2 and x x = x 2. The challenge is to find the last term of each binomial. They must be chosen so that they will cause the coefficient of the middle term and the last term of the trinomial to work out. (That’s 11 and 24 in this case. ) Their sum equals the middle term of the trinomial. + = 11 Their product of those same numbers equals the last term of the trinomial. = 24

Example 1: x 2 + 11 x + 24 List the factors of 24: 1 24 SUM = 25 2 12 SUM = 14 3 8 SUM = 11 4 6 SUM = 10 It is the factors 3 and 8 that produce a sum of 11 AND a product of 24 so they must be the last terms of each binomial. (x + 3)(x + 8)

If we multiply these factors using FOIL, we get the polynomial that we started with. (x)(x) = x 2 (x + 3)(x + 8) = x 2 + 8 x + 3 x + 24 (x)(8) = 8 x (3)(x) = 3 x (3)(8) = 24 As we look at the 4 terms above, it becomes apparent why the sum of the last terms in each binomial must be equal to the middle term of the trinomial. (x + 3)(x + 8) = x 2 + 8 x + 3 x + 24 = x 2 + 11 x + 24

Example 2: a 2 + 16 a + 28 Factors of 28: 1 28 2 14 4 7 SUM = 16 a a = a 2 so they are the first terms of each binomial and the factors 2 and 14 make a sum of 16 so the are the last terms of each binomial. = (a + 2)(a + 14)

Example 3: y 2 + 2 y + 1 = (y + 1) Factors of 1: 1 1 SUM = 2 Sometimes there is only 1 pair of factors to consider. Factors of 1: Example 4: m 2 + 3 m + 1 SUM = 3 1 1 In this example the factors available do not make a sum of 3 which means that the Factors of 120: trinomial can’t be factored. 1 120 Example 5: p 2 + 23 p + 120 In this example there are many pairs of factors to consider. Most examples will have fewer than these. The trick is in being able to quickly find all of the factors of c. p 2 + 23 p + 120 = (p + 8)(p + 15) 2 60 3 40 4 30 5 24 6 20 8 15 10 12 SUM = 23

Example 6: x 2 + 5 x + 6 = (x + 2)(x + 3) Factors of 6: 1 6 2 3 SUM = 5 In each of the preceding examples the signs of the terms in the trinomials were always positive. Now we will observe examples where the signs can be negative. Example 7: x 2 + 5 x - 6 = (x - 1)(x + 6) Factors of -6: -1 +6 -2 +3 SUM = 5 When looking for the factors of a negative number, one must be positive and the other negative. If at the same time their sum is positive, then the factor that is bigger must be the positive one.

REVIEW OF RULES FOR SIGNS ADDITION MULTIPLICATION (+)(+) = (+) + (+) = (+)(-) = (-) (+) + (-) = Sign of bigger number (-)(+) = (-) + (+) = (-)(-) = (+) (-) + (-) = (-) ( ) Example 8: x 2 - 5 x - 6 = (x + 1)(x - 6) Factors of -6: When both the product and sum are negative, the factors have opposite signs but this time the bigger factor will be negative. +1 -6 +2 -3 SUM = -5

Example 9: x 2 - 5 x + 6 = (x - 2)(x - 3) Factors of 6: -1 -6 -2 -3 SUM = -5 When looking for factors of a positive number when the sum is negative, both factors will be negative. Example 10: x 2 - 5 x - 36 = (x + 4)(x - 9) Factors of -36: 1 -36 2 -18 3 -12 4 -9 6 -6 SUM = -5

Here we go! 1) Factor y 2 + 6 y + 8 Use your factoring chart. Do we have a GCF? Nope! Is it a Diff. of Squares problem? No way! 3 terms! Now we will learn Trinomials! You will set up a table with the following information. Product of the first and last coefficients Middle coefficient The goal is to find two factors in the first column that add up to the middle term in the second column. We’ll work it out in the next few slides.

Here are some hints to help you choose your factors. 1) When the last term is positive, the factors will have the same sign as the middle term. 2) When the last term is negative, the factors will have different signs.

2) Factor 5 x 2 - 17 x + 14 Create your table. Product of the first and last coefficients Signs need to be the same as the middle sign since the product is positive. Multiply +70 -1, -70 -2, -35 -7, -10 Add -17 -71 -37 -17 Replace the middle term. 5 x 2 – 7 x – 10 x + 14 Group the terms. Middle coefficient

(5 x 2 – 7 x) (– 10 x + 14) Factor out the GCF x(5 x – 7) -2(5 x – 7) The parentheses are the same! (x – 2)(5 x – 7) Hopefully, these will continue to get easier the more you do them.
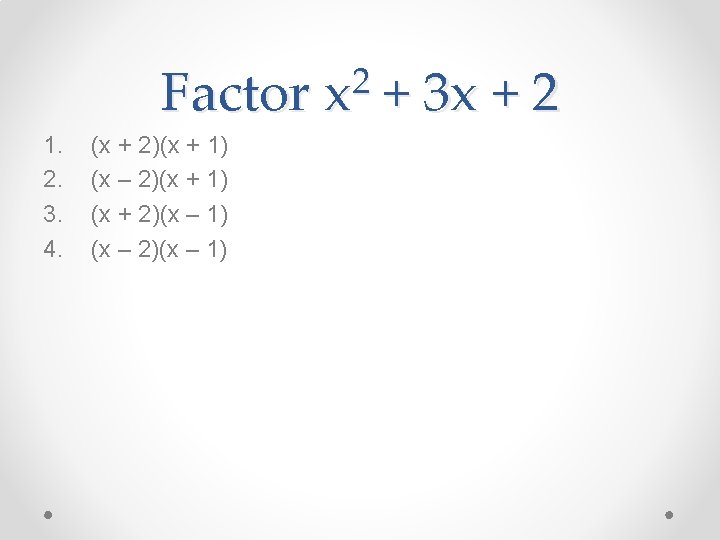

Factor 1. 2. 3. 4. (2 x + 10)(x + 1) (2 x + 5)(x + 2) (2 x + 2)(x + 5) (2 x + 1)(x + 10) 2 2 x + 9 x + 10

Factor 1. 2. 3. 4. 2 6 y (6 y 2 – 15 y)(+2 y – 5) (2 y – 1)(3 y – 5) (2 y + 1)(3 y – 5) (2 y – 5)(3 y + 1) – 13 y – 5
 Review of factoring techniques
Review of factoring techniques Criss cross method factoring
Criss cross method factoring Fonction technique scooter
Fonction technique scooter Bottoms up method factoring trinomials
Bottoms up method factoring trinomials Factor by gcf
Factor by gcf Persuasive devices quiz
Persuasive devices quiz Unit 9 factoring review answers
Unit 9 factoring review answers Review packet section 1 factoring
Review packet section 1 factoring Ch 13 factoring review worksheet
Ch 13 factoring review worksheet Factoring review
Factoring review Factoring quadratics review
Factoring quadratics review Chapter review motion part a vocabulary review answer key
Chapter review motion part a vocabulary review answer key Ap gov final review
Ap gov final review Nader amin-salehi
Nader amin-salehi Search strategy example
Search strategy example Narrative review vs systematic review
Narrative review vs systematic review Algebraic techniques year 8
Algebraic techniques year 8 Acoastmap techniques
Acoastmap techniques Bandwagon poster
Bandwagon poster Ww2 propaganda techniques
Ww2 propaganda techniques Incongruity satire definition
Incongruity satire definition Atrumatic care
Atrumatic care Wet chemical techniques
Wet chemical techniques Weaving terms
Weaving terms Wb
Wb 5 basic skills in volleyball
5 basic skills in volleyball Visual techniques in images
Visual techniques in images What are visual techniques
What are visual techniques Virtualization techniques in cloud computing
Virtualization techniques in cloud computing Taxonomy of virtualization techniques
Taxonomy of virtualization techniques Virtual memory management techniques
Virtual memory management techniques Questioning and discussion techniques
Questioning and discussion techniques Narrative devices
Narrative devices Quotation techniques
Quotation techniques Language learning software
Language learning software Fmea in tqm
Fmea in tqm Common modeling techniques of deployment diagram
Common modeling techniques of deployment diagram Total quality management tools and techniques
Total quality management tools and techniques Data input in gis
Data input in gis Satirical techniques
Satirical techniques