SEARCH TECHNIQUES SEARCH TECHNIQUES Search techniques Blind Depth

SEARCH TECHNIQUES

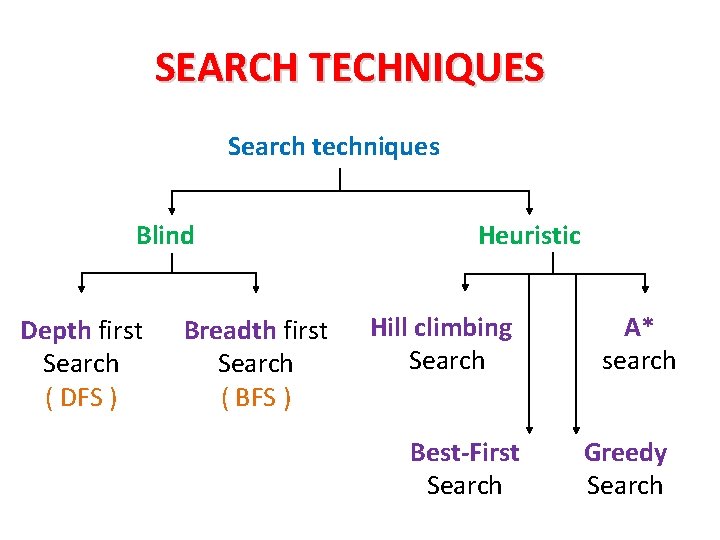
SEARCH TECHNIQUES Search techniques Blind Depth first Search ( DFS ) Breadth first Search ( BFS ) Heuristic Hill climbing Search Best-First Search A* search Greedy Search

BLIND SEARCH ALGORITHM 1. Depth First Search ( DFS ) : The algorithm : open : = [ start ]; closed : = [ ]; while open != [ ] do remove leftmost state from open, call it X; if X is a goal then return success; else begin generate children of X ; put X on closed; eliminate children of X if already in open or closed; put other children in order on left end of open; end while return failure;

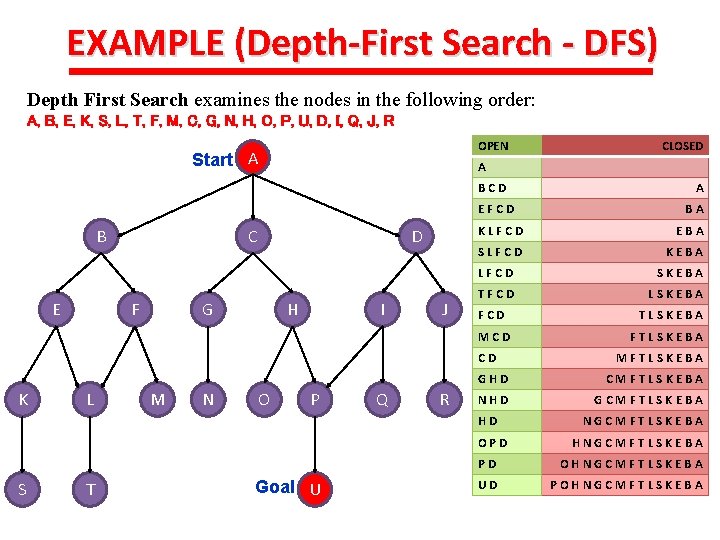
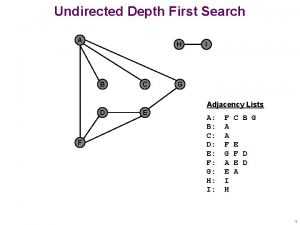
EXAMPLE (Depth-First Search - DFS) Depth First Search examines the nodes in the following order: A, B, E, K, S, L, T, F, M, C, G, N, H, O, P, U, D, I, Q, J, R OPEN Start A A BCD EFCD B E C F D G H I J M N O P Q R SLFCD KEBA LFCD SKEBA TFCD LSKEBA FCD Goal U FTLSKEBA MFTLSKEBA CMFTLSKEBA NHD GCMFTLSKEBA OPD T TLSKEBA GHD HD S BA EBA CD L A KLFCD MCD K CLOSED NGCMFTLSKEBA HNGCMFTLSKEBA PD OHNGCMFTLSKEBA UD POHNGCMFTLSKEBA

Depth-First Search (DFS) A go(X, X, [X]). go(X, Y, [X|T]): link(X, Z), go(Z, Y, T). | ? - go(a, c, X). X = [a, e, f, c] ? ; X = [a, b, c] ? ; no E D B F F C C C • This simple search algorithm uses Prolog’s unification routine to find the first link from the current node then follows it. • It always follows the left-most branch of the search tree first; following it down until it either finds the goal state or hits a deadend. It will then backtrack to find another branch to follow. = depth-first search.

BLIND SEARCH ALGORITHM 2. Breadth First Search ( BFS ) : The algorithm : open : = [ start ]; closed : = [ ]; while open != [ ] do remove leftmost state from open, call it X; if X is a goal then return success; else begin generate children of X ; put X on closed; eliminate children of X if already in open or closed; put other children in order on right end of open; end while return failure;

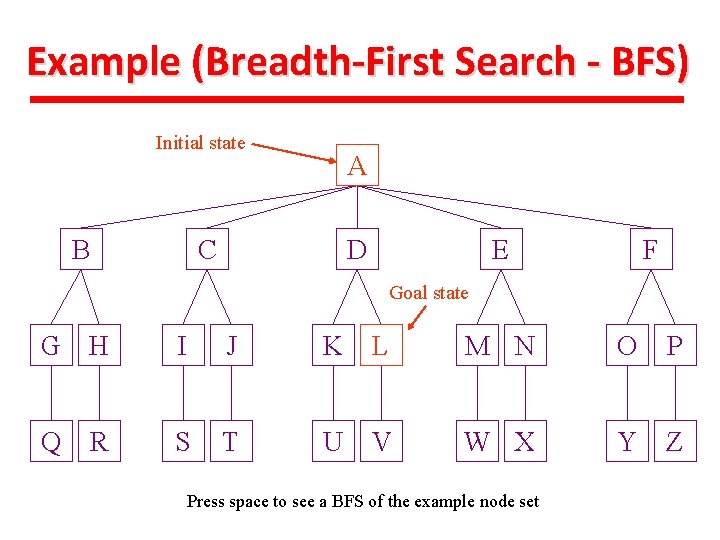
Example (Breadth-First Search - BFS) Initial state B A C D E F Goal state G H I J K L M N O P Q S T U V W X Y Z R Press space to see a BFS of the example node set

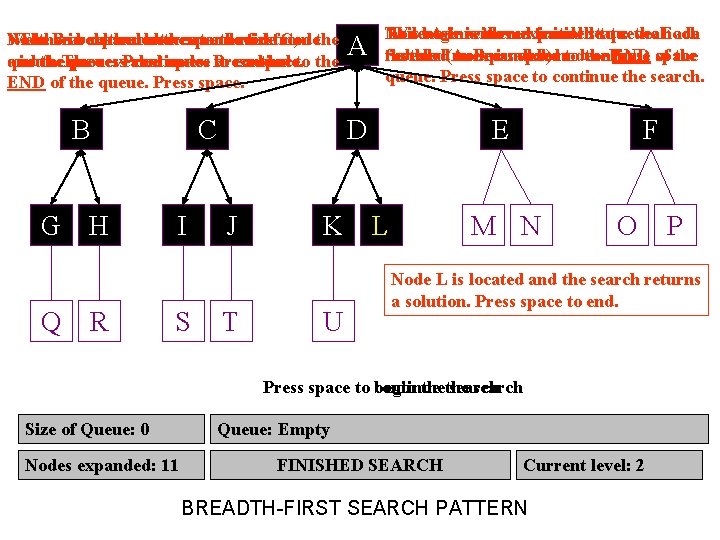
Node B isbacktrack expanded then removed We The then search then moves to expand to thenode firstfrom C, nodethe queue. revealed nodes arecontinue. added and in the. The queue. process Press continues. space Press to spaceto the END of the queue. Press space. B G H Q R C I S A Node A is removed from This We begin node is with then our expanded initialthe state: toqueue. reveal the Each node revealed node is added to the END space of the further labeled(unexpanded) A. Press spacenodes. continue Press queue. Press space to continue the search. D J T K U E L F M N O P Node L is located and the search returns a solution. Press space to end. Press space to begin continue thethe search Size of Queue: 010 987651 Queue: Empty A J, B, C, D, E, F, G, H, I, J, K, L, K, G, C, F, M, D, E, H, K, I, L, J, G, L, H, D, F, M, E, I, N, L, K, J, M, G, H, E, F, I, O, N, M, K, L, J, G, H, F I, N, P, O, K, M, J, L, N, H I, O, Q, P, K, L, M, JO, N, P, R, Q, LP, M, O, N, Q, S, R, Q, N O, P, R, T, S, R Q PU ST Nodes expanded: 11 9876543210 10 Current. FINISHED Action: Backtracking Expanding SEARCH Current level: 210 n/a BREADTH-FIRST SEARCH PATTERN

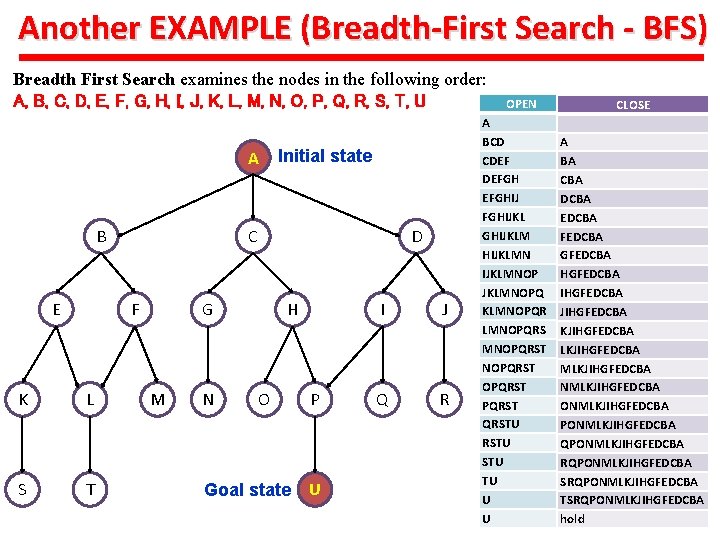
Another EXAMPLE (Breadth-First Search - BFS) Breadth First Search examines the nodes in the following order: A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U A B E C F K L S T Initial state D G M N H O Goal state P U I J Q R OPEN A BCD CDEF DEFGHIJ FGHIJKLM HIJKLMNOP JKLMNOPQR LMNOPQRST OPQRSTU STU TU U U CLOSE A BA CBA DCBA EDCBA FEDCBA GFEDCBA HGFEDCBA IHGFEDCBA JIHGFEDCBA KJIHGFEDCBA LKJIHGFEDCBA MLKJIHGFEDCBA NMLKJIHGFEDCBA ONMLKJIHGFEDCBA PONMLKJIHGFEDCBA QPONMLKJIHGFEDCBA RQPONMLKJIHGFEDCBA SRQPONMLKJIHGFEDCBA TSRQPONMLKJIHGFEDCBA hold

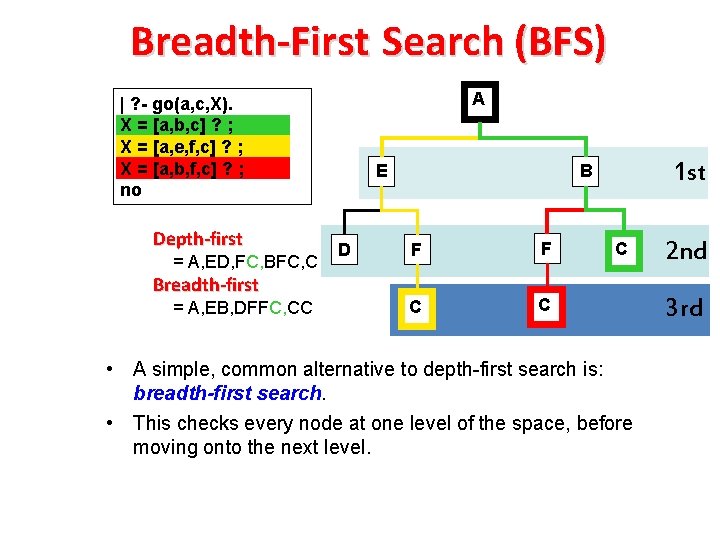
Breadth-First Search (BFS) A | ? - go(a, c, X). X = [a, b, c] ? ; X = [a, e, f, c] ? ; X = [a, b, f, c] ? ; no Depth-first = A, ED, FC, BFC, C Breadth-first = A, EB, DFFC, CC E D 1 st B F F C C C • A simple, common alternative to depth-first search is: breadth-first search. • This checks every node at one level of the space, before moving onto the next level. 2 nd 3 rd

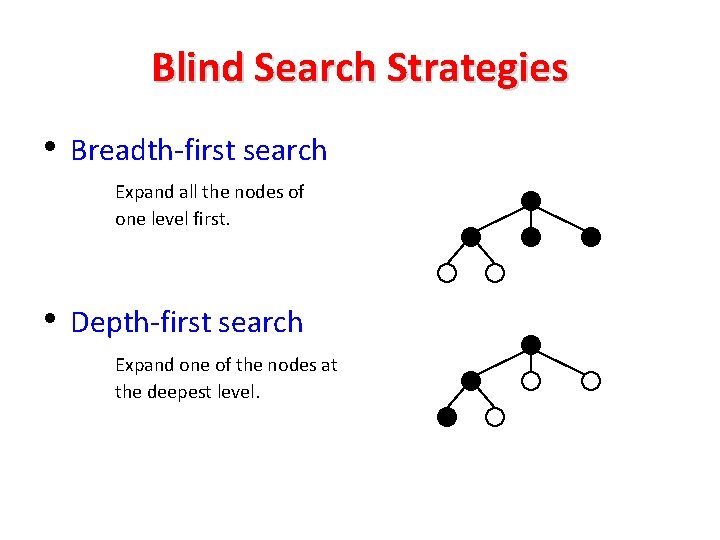
Blind Search Strategies • Breadth-first search Expand all the nodes of one level first. • Depth-first search Expand one of the nodes at the deepest level.

What is the Complexity of Breadth-First Search? • Time Complexity – assume (worst case) that there is 1 goal leaf at the RHS – so BFS will expand all nodes d=0 d=1 = 1 + b 2+ = O (bd) . . + bd d=2 G • Space Complexity – how many nodes can be in the queue (worst-case)? – at depth d-1 there are bd unexpanded nodes in the Q = O (bd) d=0 d=1 d=2 G

Examples of Time and Memory Requirements for Breadth-First Search Depth of Solution Nodes Expanded. Time 0 1 1 millisecond 100 bytes 2 111 0. 1 seconds 11 kbytes 4 11, 111 11 seconds 1 megabyte 8 108 31 hours 11 giabytes 12 1012 35 years 111 terabytes Memory Assuming b=10, 1000 nodes/sec, 100 bytes/node

What is the Complexity of Depth-First Search? • Time Complexity – assume (worst case) that there is 1 goal leaf at the RHS – so DFS will expand all nodes =1 + b 2+. . + bd = O (bd) = O (bm) • Space Complexity – how many nodes can be in the queue (worst-case)? – at depth l < d (max) we have b-1 nodes So we have (d-1)*(b-1) nodes – at max. depth d we have b nodes – total = (d-1)*(b-1) + b = O(bd) = O(bm) d=0 d=1 d=2 G d=0 d=1 d=2 d=3 d=4

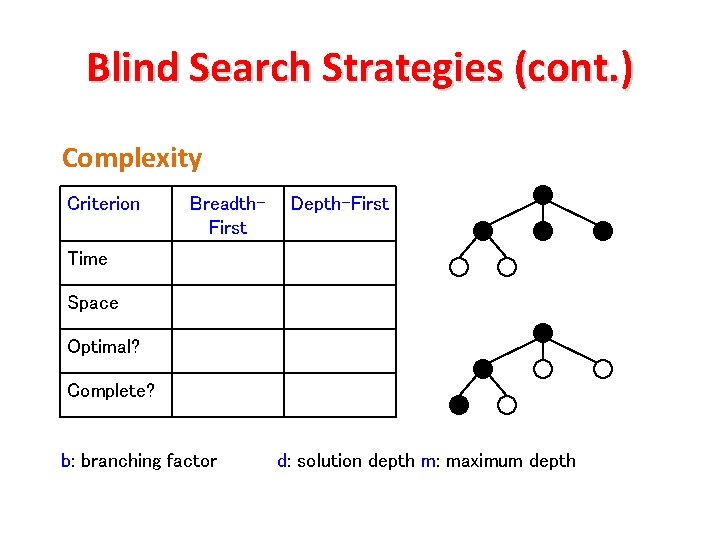
Blind Search Strategies (cont. ) Complexity Criterion Breadth. First Depth-First Time Space Optimal? Complete? b: branching factor d: solution depth m: maximum depth

Blind Search Strategies (cont. ) Complexity Criterion Breadth-First Depth-First Time bd bm Space bd bm Optimal? Yes No if we guarantee that deeper solutions are less optimal, e. g. step-cost=1 It may find a nonoptimal goal first Yes No Complete? it always reaches goal (if b is finite) b: branching factor Fails in infinitedepth spaces d: solution depth m: maximum depth

Depth-first vs. Breadth-first Advantages of depth-first: Advantages of breadth-first: • Simple to implement; • Needs relatively small memory for storing the state-space. • Guaranteed to find a solution (if one exists) - complete; • Depending on the problem, can be guaranteed to find an optimal solution. Disadvantages of depth-first: Disadvantages of breadth-first: • Sometimes fail to find a solution (may be get stuck in an infinite long branch) - not complete; • More complex to implement; • Needs a lot of memory for storing the state space if the search space has a high branching factor. • Not guaranteed to find an optimal solution (may not find the shortest path solution); • Can take a lot longer to find a solution.

Depth-first vs. Breadth-first Would you use breadth-first or depth-first search for each of the following problems? What would you base your choice on: (a) A medical diagnostic program. Usually done depth-first. This allows the program to follow a line of reasoning and only change to a new goal or hypothesis when a previous one is confirmed or denied. (b) A program to determine the best sequence of manufacturing steps to go from raw materials to a finished product. It should have breadth-first. (because it is optimal and complete)

HEURISTIC SEARCH ALGORITHM Heuristic : we use heuristic function or knowledge in order to explore the most promising state first. [Heuristics are formalized as rules for choosing those branches in a state space that are most likely to lead to an acceptable solution] This may lead to sub-optimal solution or fail to find any solution. (i. e. , heuristics do not guarantee best solution or even a solution) AI problem-solver employ heuristic into basic situations : 1. Problem may not have an exact solution because of inherent ambiguities in a problem statement or available data (Examples: medical diagnosis, vision). 2. Inefficient exact method to solve the problem (not feasible to examine every state ( e. g. theorem proving and chess game).

EXAMPLE Heuristic function for 8 -tile puzzle 1. The number of states out of place. [the state that has fewest tiles out of place is probably closer to the desired goal and would be best to examine next] 2. The summation distance between each tile and it’s correct position in the goal state.

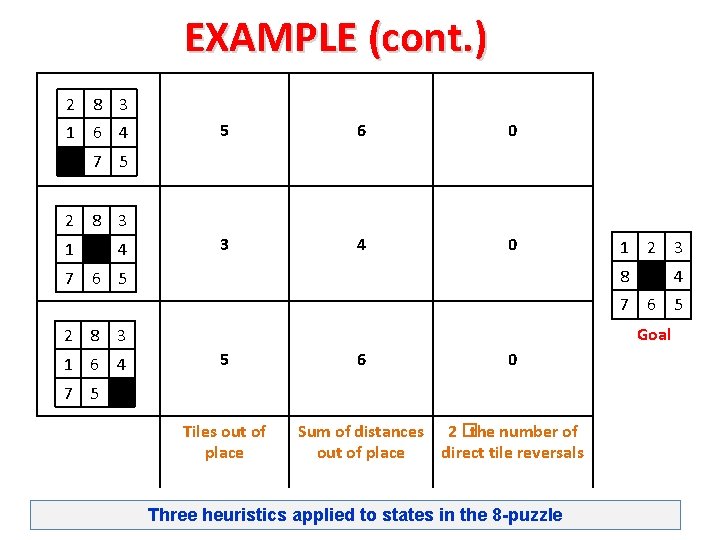
EXAMPLE (cont. ) 2 8 3 1 6 4 5 6 0 3 4 0 7 5 2 8 3 1 4 1 2 3 8 7 6 5 4 7 6 5 Goal 2 8 3 1 6 4 5 6 0 7 5 Tiles out of place Sum of distances 2 �the number of out of place direct tile reversals Three heuristics applied to states in the 8 -puzzle

HILL-CLIMBING SEARCH - Expand the current state in the search and evaluate it’s children. - The best child is selected for further expansion. - neither it sibling nor its parent are retained. - Search halts when it reaches a state that is better than any of its children. (i. e. The process ends when all operators have been applied and none of the resulting states are better than the current state) - Ve : 1. Local maximum. 2. Flat area. 3. Cant backtrack. (WHY? ) + Ve : Low memory requirement.

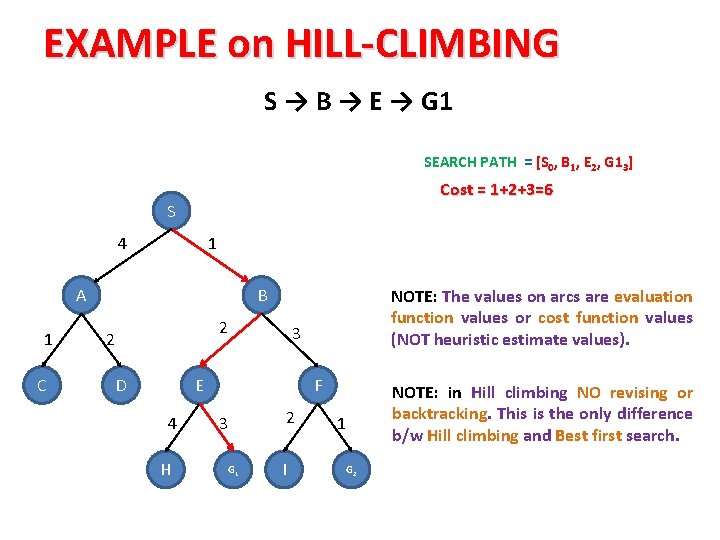
EXAMPLE on HILL-CLIMBING S → B → E → G 1 SEARCH PATH = [S 0, B 1, E 2, G 13] Cost = 1+2+3=6 S 4 1 A 1 C B 2 2 D 3 E 4 H NOTE: The values on arcs are evaluation function values or cost function values (NOT heuristic estimate values). F 2 3 G 1 I NOTE: in Hill climbing NO revising or backtracking. This is the only difference b/w Hill climbing and Best first search. 1 G 2

HILL-CLIMBING SEARCH (cont. ) • Hill climbing is an optimization technique which belongs to the family of local search. It is best used in problems with “the property that the state description itself contains all the information needed for a solution” The algorithm is memory efficient since it does not maintain a search tree: It looks only at the current state and immediate future states. • Hill climbing attempts to iteratively improve the current state by means of an evaluation function. “Consider all the [possible] states laid out on the surface of a landscape. The height of any point on the landscape corresponds to the evaluation function of the state at that point”.

HILL-CLIMBING SEARCH (cont. ) • In contrast with other iterative improvement algorithms, hill-climbing always attempts to make changes that improve the current state. In other words, hill-climbing can only advance if there is a higher point in the adjacent landscape. For example, hill climbing can be applied to the travelling salesman problem. It is easy to find an initial solution that visits all the cities but will be very poor compared to the optimal solution. The algorithm starts with such a solution and makes small improvements to it, such as switching the order in which two cities are visited. Eventually, a much shorter route is likely to be obtained.

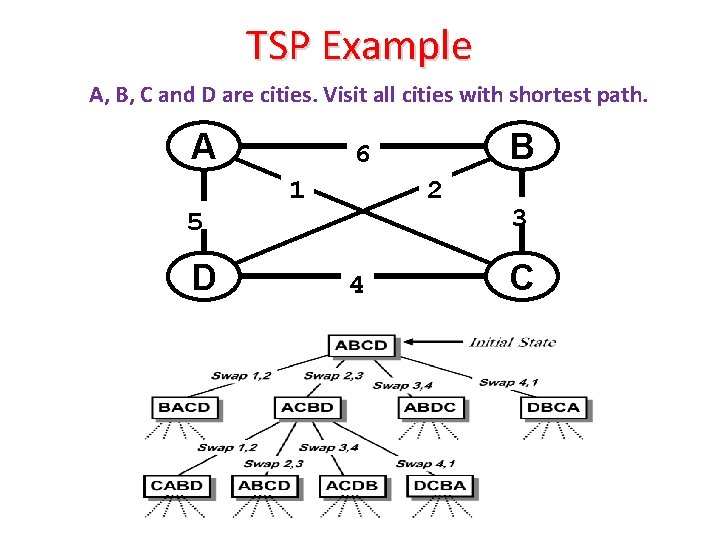
TSP Example A, B, C and D are cities. Visit all cities with shortest path. A 5 D B 6 1 2 4 3 C

HILL-CLIMBING SEARCH (cont. ) • Hill Climbing can get stuck at local maxima. Consider the following tree. a is an initial state and h and k are final states. The numbers near the states are the heuristic values. • When hill climbing is run on the tree, we get a -> f -> g and here we get stuck at local maxima g. Hill climbing can't go back and make a new choice (for example j or e) because it keeps no history. So how to avoid this stuck in order to get global maxima.

HILL-CLIMBING SEARCH (cont. ) • A common way to avoid getting stuck in local maxima with Hill Climbing is to use random restarts. In our example, if g is a local maxima, the algorithm would stop there and then pick another random node to restart from. So if j or c were picked (or possibly a, b, or d) you would find the global maxima in h or k. If once again you get stuck at some local maxima you have to restart again with some other random node. Generally there is a limit on the no. of times you can re-do this process of finding the optimal solution. After you reach this limit, you select the least amongst all the local maxima you reached during the process. Clean and repeat enough times (iterative) and you'll find the global maxima or something close. • Hill Climbing is NOT complete and can NOT guarantee to find the global maxima. The benefit is that it requires a fraction of the resources; it's a very effective solution (optimization).

BEST FIRST SEARCH Definition • Is another more informed heuristic algorithm. • Best-first search in its most general form is a simple heuristic search algorithm. • “Heuristic” here refers to a general problem-solving rule or set of rules that do not guarantee the best solution or even any solution, but serves as a useful guide for problem-solving. • Best-first search is a graph-based search algorithm, meaning that the search space can be represented as a series of nodes connected by paths.

BEST FIRST SEARCH (cont. ) How it works • The name “best-first” refers to the method of exploring the node with the best “score” first. • An evaluation function is used to assign a score to each candidate node. • The algorithm maintains two lists, one containing a list of candidates yet to explore (OPEN), and one containing a list of already visited nodes (CLOSED). States in OPEN are ordered according to some heuristic estimate of their “closeness” to a goal. This ordered OPEN list is referred to as priority queue. • Since all unvisited successor nodes of every visited node are included in the OPEN list, the algorithm is not restricted to only exploring successor nodes of the most recently visited node. In other words, the algorithm always chooses the best of all unvisited nodes that have been graphed, rather than being restricted to only a small subset, such as immediate neighbors. Other search strategies, such as depth-first and breadthfirst, have this restriction. • The advantage of this strategy is that if the algorithm reaches a deadend node, it will continue to try other nodes. `

BEST FIRST SEARCH (cont. ) Algorithm Best-first search in its most basic form consists of the following algorithm : 1. The 1 st step is to define the OPEN list with a single node, the starting node. 2. The 2 nd step is to check whether or not OPEN is empty. If it is empty, then the algorithm returns failure and exits. 3. The 3 rd step is to remove the node with the best score, n, from OPEN and place it in CLOSED. 4. The 4 th step “expands” the node n, where expansion is the identification of successor nodes of n. 5. The 5 th step then checks each of the successor nodes to see whether or not one of them is the goal node. If any successor is the goal node, the algorithm returns success and the solution, which consists of a path traced backwards from the goal to the start node. Otherwise, proceeds to the sixth step. 6. In 6 th step, for every successor node, the algorithm applies the evaluation function, f, to it, then checks to see if the node has been in either OPEN or CLOSED. If the node has not been in either, it gets added to OPEN. 7. Finally, the 7 th step establishes a looping structure by sending the algorithm back to the 2 nd step. This loop will only be broken if the algorithm returns success in step 5 or failure in step 2.

BEST FIRST SEARCH (cont. ) Algorithm (con. ) The algorithm is represented here in pseudo-code: 1. Define a list, OPEN, consisting solely of a single node, the start node, s. 2. IF the list is empty, return failure. 3. Remove from the list the node n with the best score (the node where f is the minimum), and move it to a list, CLOSED. 4. Expand node n. 5. IF any successor to n is the goal node, return success and the solution (by tracing the path from the goal node to s). 6. FOR each successor node: a) apply the evaluation function, f, to the node. b) IF the node has not been in either list, add it to OPEN. 7. Looping structure by sending the algorithm back to the 2 nd step.

EXAMPLE on Best-First Search NOTE: similar to Hill climbing but open=[S 0]; closed=[ ] WITH revising or backtracking open=[B 1 , A 4]; closed=[S 0] (keeping track of visited nodes). open=[E 3 , A 4, F 4 ]; closed=[S 0 , B 1] open=[A 4 , F 4 , G 16 , , H 7]; closed=[S 0 , B 1 , E 3] open=[F 4 , C 5 , G 16, D 6 , H 7]; closed=[S 0 , B 1 , E 3 , A 4] open=[C 5 , G 25 , G 16 , I 6 , D 6 , H 7]; closed=[S 0 , B 1 , E 3 , A 4 , F 4] open=[G 25 , G 16 , I 6 , D 6 , H 7]; closed=[S 0 , B 1 , E 3 , A 4 , F 4 , C 5] S 4 SEARCH PATH = [S 0 , B 1 , E 3 , A 4 , F 4 , C 5 , G 25] 1 A 1 C B Cost = 1+3+1=5 2 2 D 3 E 4 H F 2 3 G 1 I 1 G 2

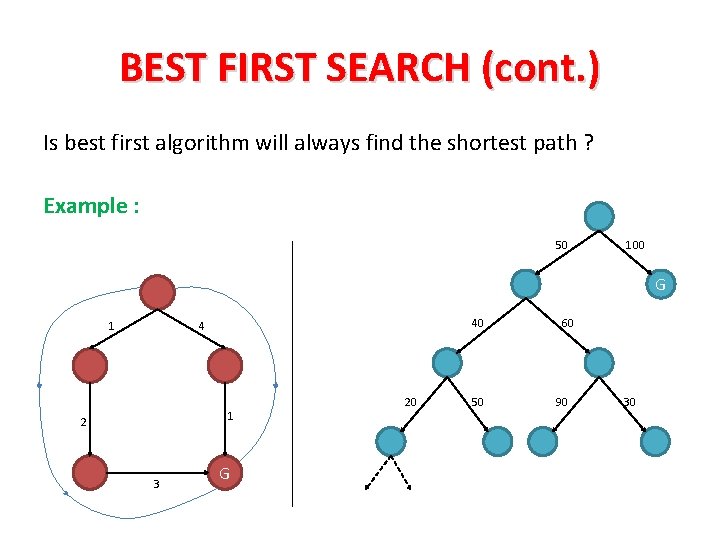
BEST FIRST SEARCH (cont. ) Is best first algorithm will always find the shortest path ? Example : 50 100 G 1 40 4 1 2 3 G 20 50 60 90 30

BEST FIRST SEARCH (cont. ) 1. It may get stuck in an infinite branch that doesn’t contain the goal. 2. It’s not guarantee to find the shortest path solution. Memory requirement : In best case : as depth first search. In average case : between depth and breadth. In worst case : as breadth first search.

GREEDY BEST FIRST SEARCH Ø Greedy best-first search is a best first search but uses heuristic estimate h(n) rather than cost function. Ø Both follow the same process but Greedy uses heuristic function whereas best first uses cost function. Ø EXAMPLE: S: Initial state, G 1, G 2: goal. Table shows the heuristic estimates: node h(n) A B C 11 5 9 D E F S NOTE: similar to Best first search but uses heuristic values. 8 4 2 H I C A B D E F 7 3 H G 1 I G 2

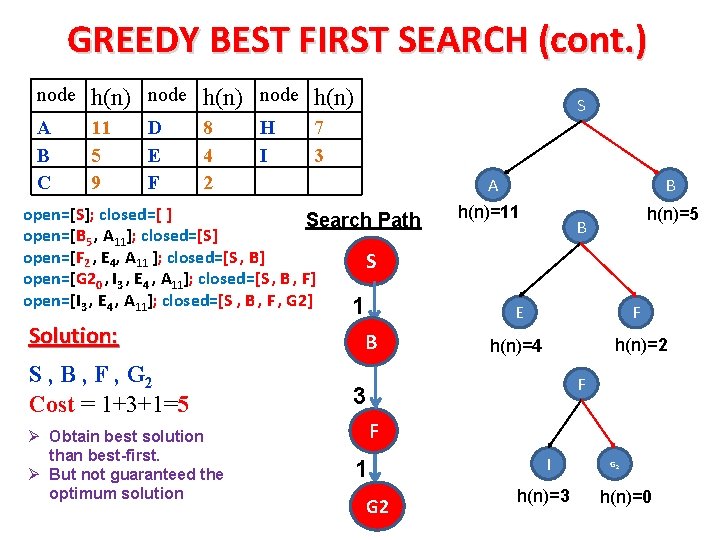
GREEDY BEST FIRST SEARCH (cont. ) node h(n) A B C 11 5 9 D E F 8 4 2 H I S 7 3 A open=[S]; closed=[ ] Search Path open=[B 5 , A 11]; closed=[S] open=[F 2 , E 4, A 11 ]; closed=[S , B] S open=[G 20 , I 3 , E 4 , A 11]; closed=[S , B , F] open=[I 3 , E 4 , A 11]; closed=[S , B , F , G 2] 1 Solution: S , B , F , G 2 Cost = 1+3+1=5 Ø Obtain best solution than best-first. Ø But not guaranteed the optimum solution B B h(n)=11 h(n)=5 B E F h(n)=2 h(n)=4 F 3 F 1 G 2 I h(n)=3 G 2 h(n)=0

SOLUTIONS AND A ALGORITHM Solution for the worst case : we will use the n-beam search algorithm , that keep just the best states in the memory. Solution for the not finding the goal or shortest path : Is to use heuristic function that takes into consider how far a state from initial state , so that for any state : f(n)=g(n)+h(n) A algorithm Where : g ( n ) : measures the distance between the initial state and state of n. [actual length of the path start - n] h ( n ) : is a heuristic estimate of the distance from state n to a goal.

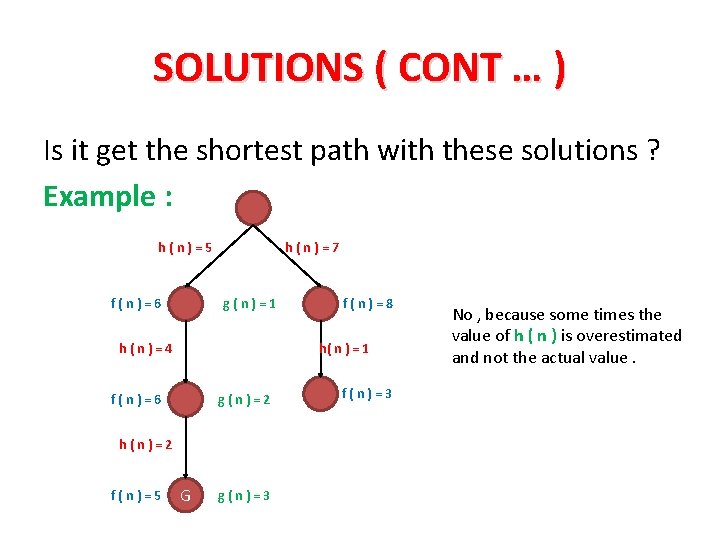
SOLUTIONS ( CONT … ) Is it get the shortest path with these solutions ? Example : h(n)=5 f(n)=6 h(n)=7 g(n)=1 h(n)=4 h( n ) = 1 f(n)=6 g(n)=2 h(n)=2 f(n)=5 f(n)=8 G g(n)=3 f(n)=3 No , because some times the value of h ( n ) is overestimated and not the actual value.

A AND A* ALGORITHM F ( n ) is used to avoid getting stuck in an infinite long branch. When the best first search algorithm use the format : f ( n ) = h ( n ) + g ( n ) , then it will be called A algorithm But A algorithm doesn’t always give us the shortest path , because of overestimate for h ( n ) Example : in the last graph , h ( n ) = 7 that’s mean we need to 7 movement to reach the goal.

A* ALGORITHM Ø If we guarantee that there is no overestimate for h(n), we will guarantee that f(n) = h(n) + g(n) give us the shortest path, If h(n) <= h*(n) for all n. Ø If h(n) <= h*(n) then h(n) is called Admissible heuristic where : h(n) is the heuristic value. h*(n) is the actual value. This algorithm called A* algorithm. A* Algorithm f(n) = h(n) + g(n)

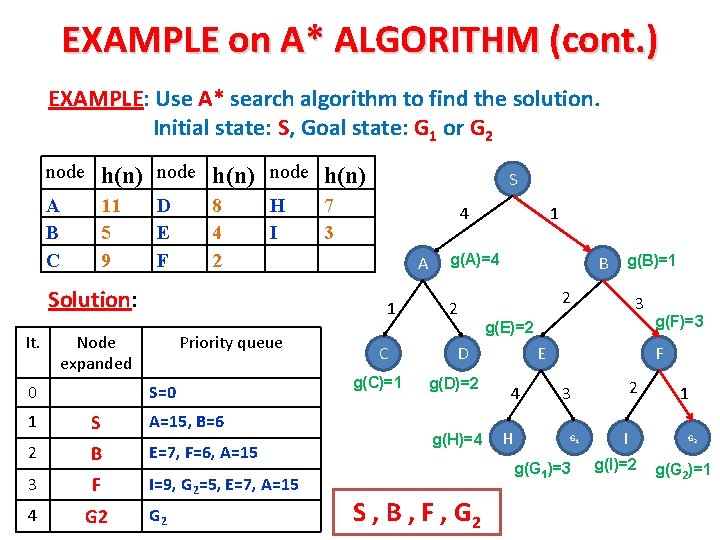
EXAMPLE on A* ALGORITHM (cont. ) EXAMPLE: Use A* search algorithm to find the solution. Initial state: S, Goal state: G 1 or G 2 node h(n) A B C 11 5 9 D E F 8 4 2 H I Solution: It. 7 3 4 A 1 Node expanded 0 S Priority queue S=0 1 S A=15, B=6 2 B E=7, F=6, A=15 3 F I=9, G 2=5, E=7, A=15 4 G 2 C g(C)=1 1 g(A)=4 2 B 2 g(H)=4 E 4 H g(F)=3 F 2 3 G 1 g(G 1)=3 S , B , F , G 2 3 g(E)=2 D g(D)=2 g(B)=1 I g(I)=2 1 G 2 g(G 2)=1

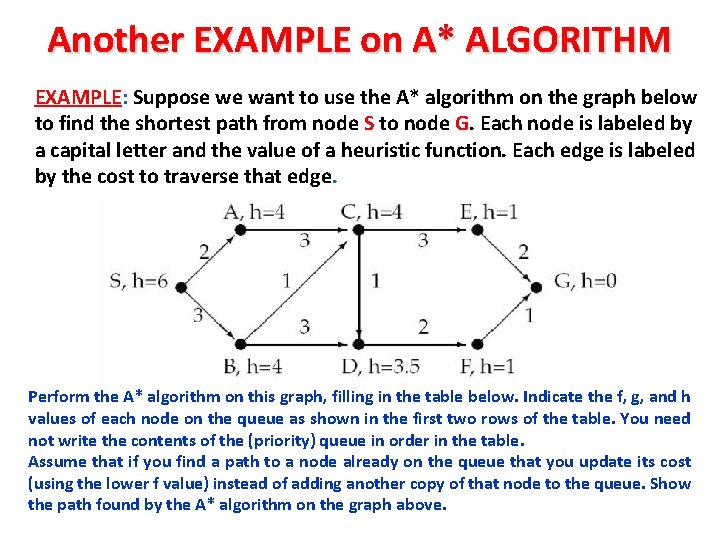
Another EXAMPLE on A* ALGORITHM EXAMPLE: Suppose we want to use the A* algorithm on the graph below to find the shortest path from node S to node G. Each node is labeled by a capital letter and the value of a heuristic function. Each edge is labeled by the cost to traverse that edge. Perform the A* algorithm on this graph, filling in the table below. Indicate the f, g, and h values of each node on the queue as shown in the first two rows of the table. You need not write the contents of the (priority) queue in order in the table. Assume that if you find a path to a node already on the queue that you update its cost (using the lower f value) instead of adding another copy of that node to the queue. Show the path found by the A* algorithm on the graph above.

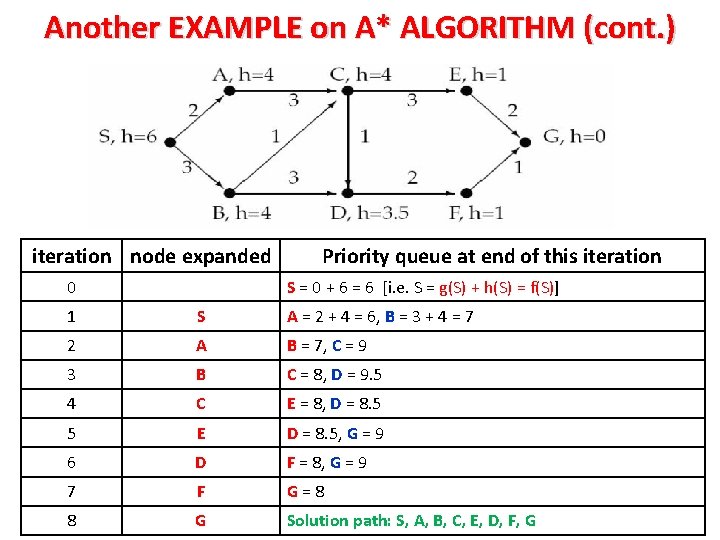
Another EXAMPLE on A* ALGORITHM (cont. ) iteration node expanded 0 Priority queue at end of this iteration S = 0 + 6 = 6 [i. e. S = g(S) + h(S) = f(S)] 1 S A = 2 + 4 = 6, B = 3 + 4 = 7 2 A B = 7, C = 9 3 B C = 8, D = 9. 5 4 C E = 8, D = 8. 5 5 E D = 8. 5, G = 9 6 D F = 8, G = 9 7 F G=8 8 G Solution path: S, A, B, C, E, D, F, G