Review Factoring Techniques for the Final Exam Factoring









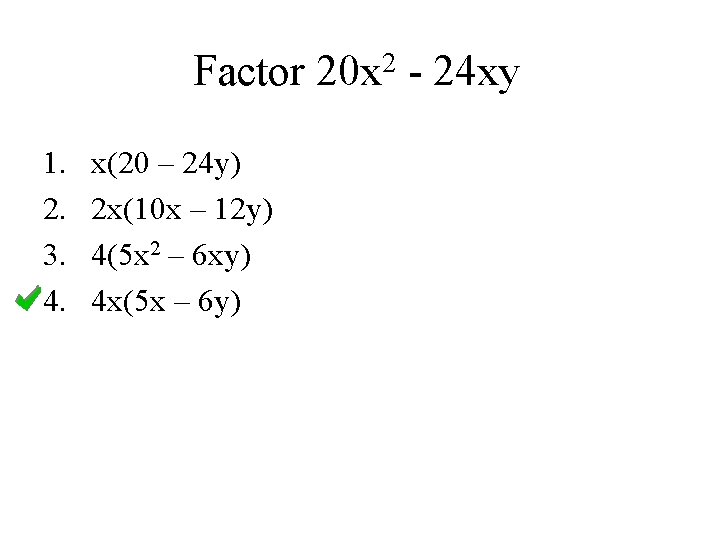

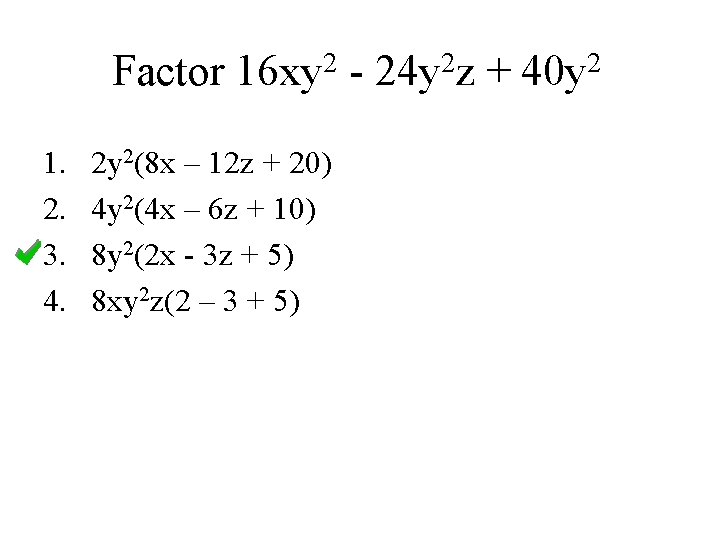

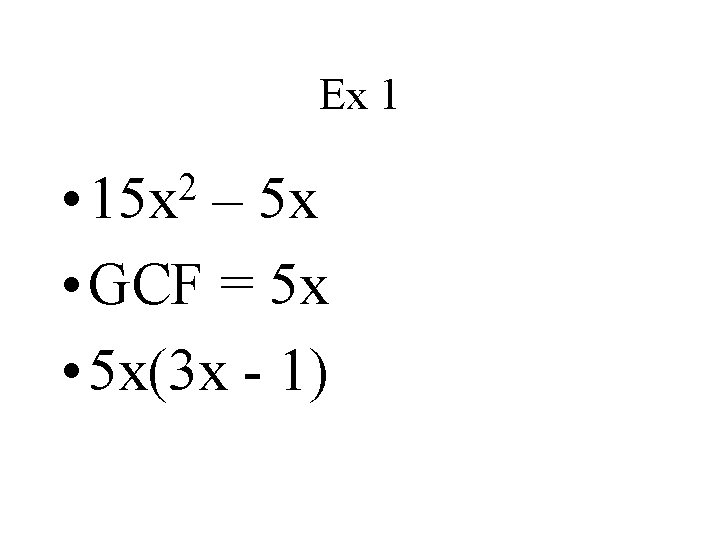
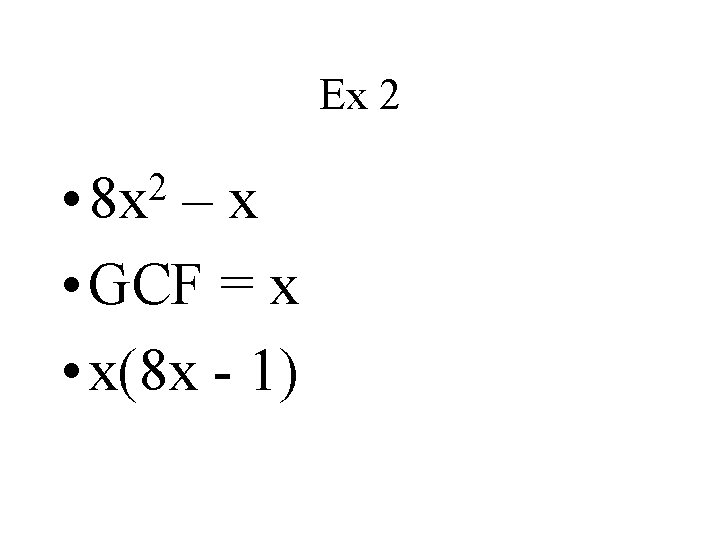
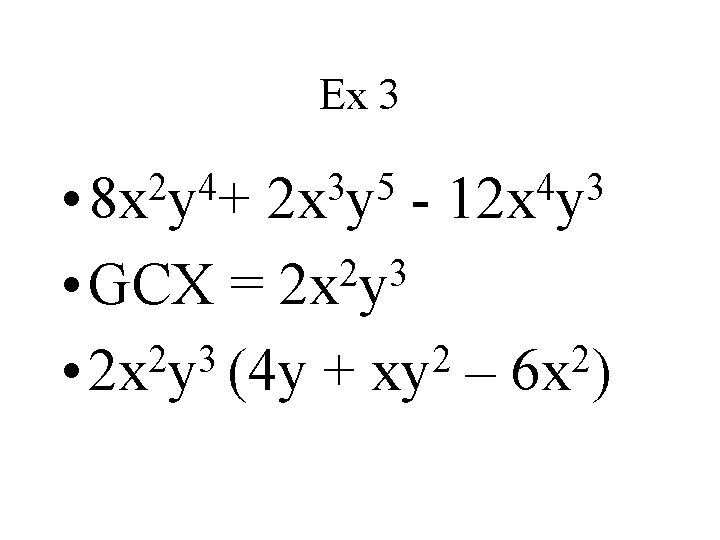




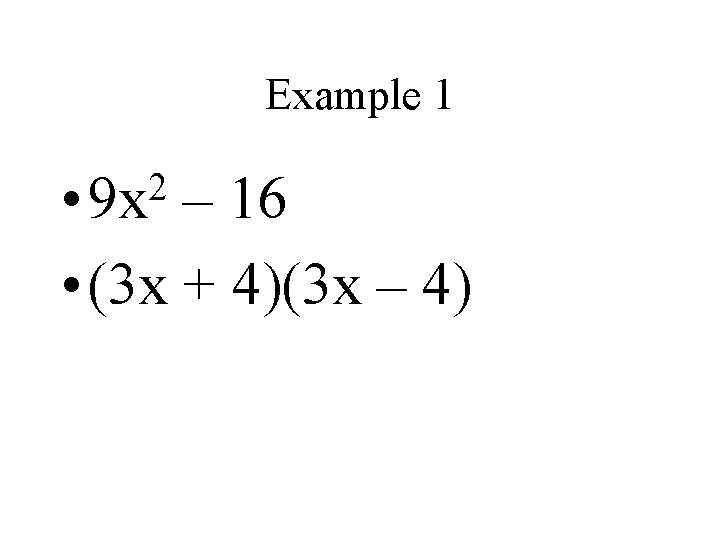
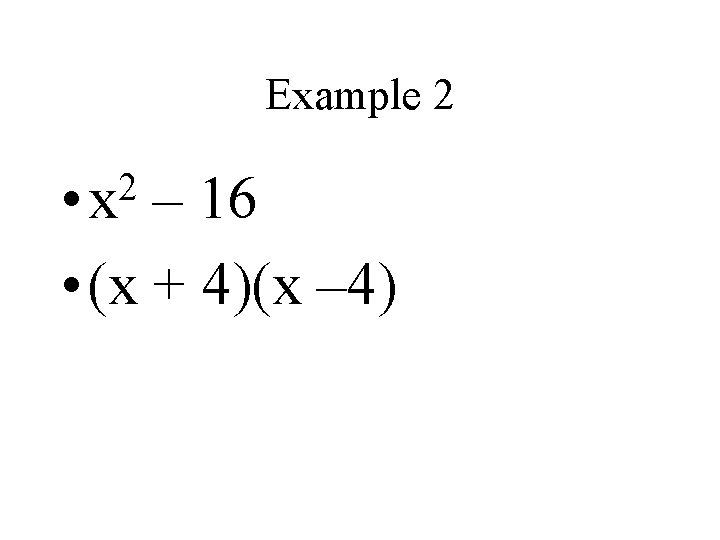
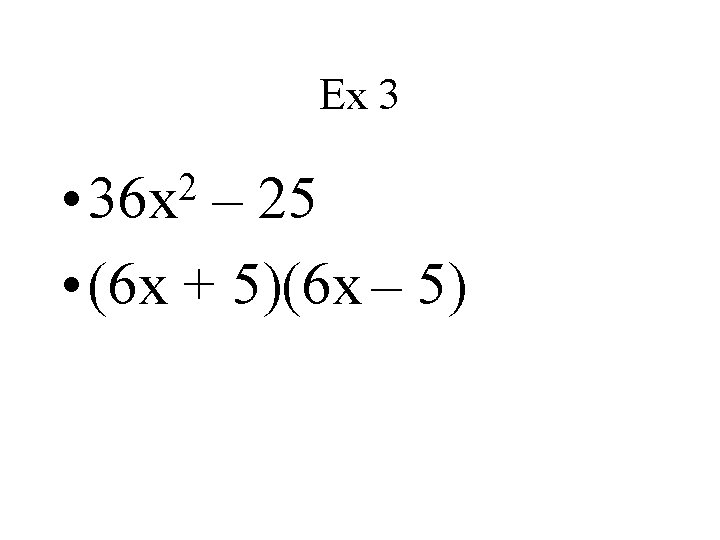

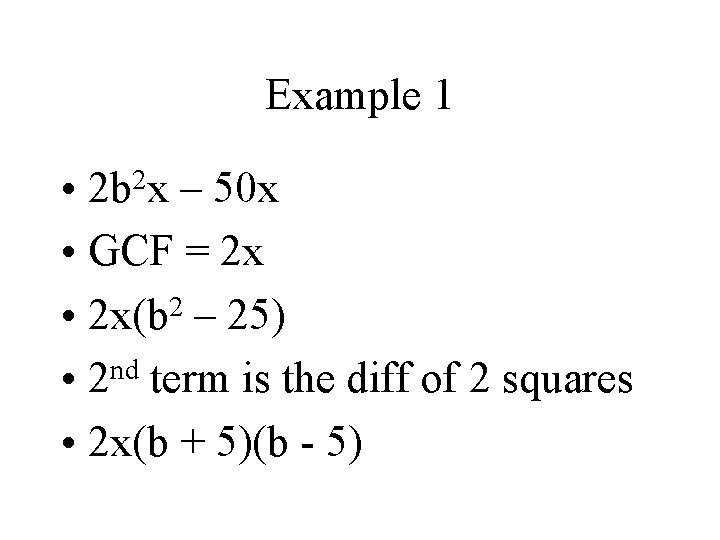


















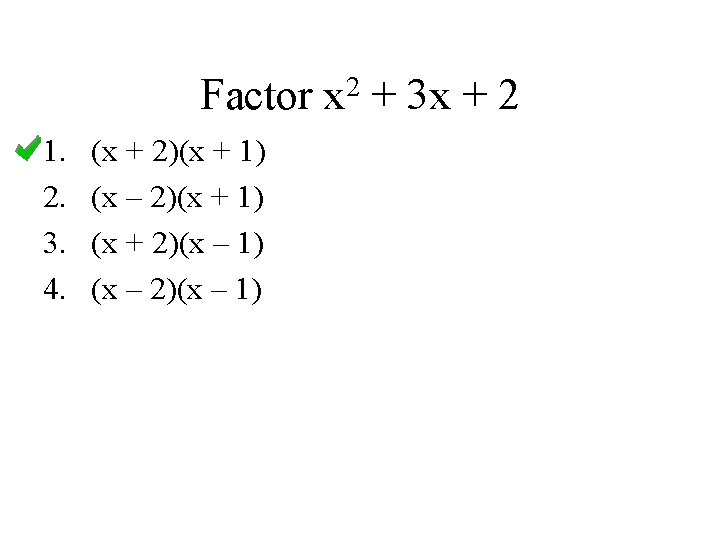
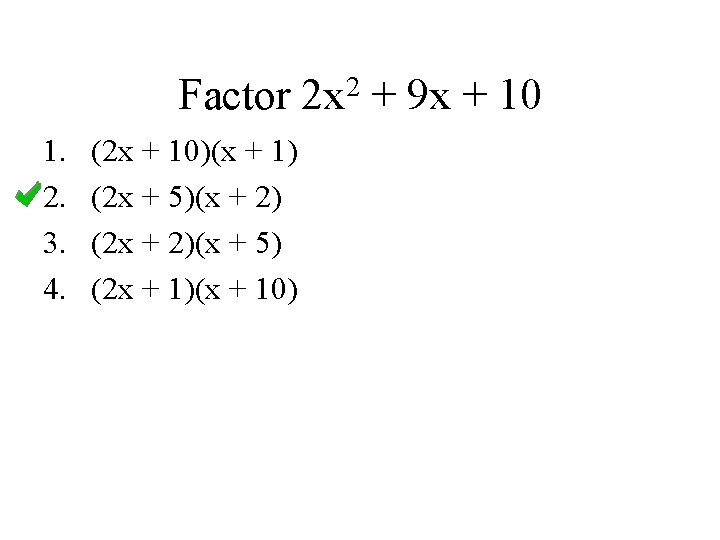
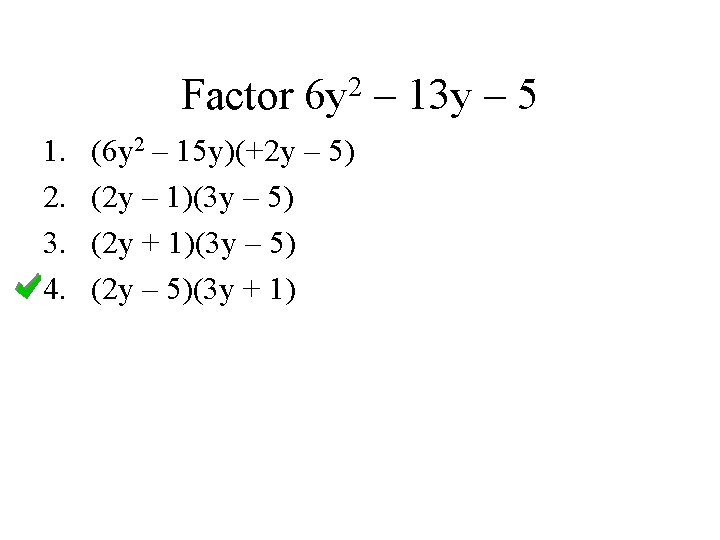

![2[(x 2 – x)(– 6 x + 6)] Factor out the GCF 2[x(x – 2[(x 2 – x)(– 6 x + 6)] Factor out the GCF 2[x(x –](https://slidetodoc.com/presentation_image_h2/8f0e1fe752b2c41a5723f103a281d100/image-51.jpg)
- Slides: 51

Review Factoring Techniques for the Final Exam

Factoring? • Factoring is a method to find the basic numbers and variables that made up a product. • (Factor) x (Factor) = Product • Some numbers are Prime, meaning they are only divisible by themselves and 1 and not factorable.

When factoring trinomials, we always try GCF method first!!!! Number of terms Factoring Technique 2 Difference of 2 Squares 3 Sum and Product Method 4 or 6 Grouping

GCF Method

Warm-UP - Distribute each problem:

GCF Method is just distributing backwards!!

Review: What is the GCF of 25 a 2 and 15 a? 5 a Let’s go one step further… 1) FACTOR 25 a 2 + 15 a. Find the GCF and divide each term 25 a 2 + 15 a = 5 a( ___ 5 a + ___ 3 ) Check your answer by distributing.

2) Factor 18 x 2 - 12 x 3. Find the GCF 6 x 2 Divide each term by the GCF 18 x 2 - 12 x 3 = 6 x 2( ___ 3 - ___ 2 x ) Check your answer by distributing.

3) Factor 2 28 a b + 2 56 abc. GCF = 28 ab Divide each term by the GCF 2 2 2 a 2 c 28 a b + 56 abc = 28 ab ( ___ + ___ ) Check your answer by distributing. 28 ab(a + 2 c 2)
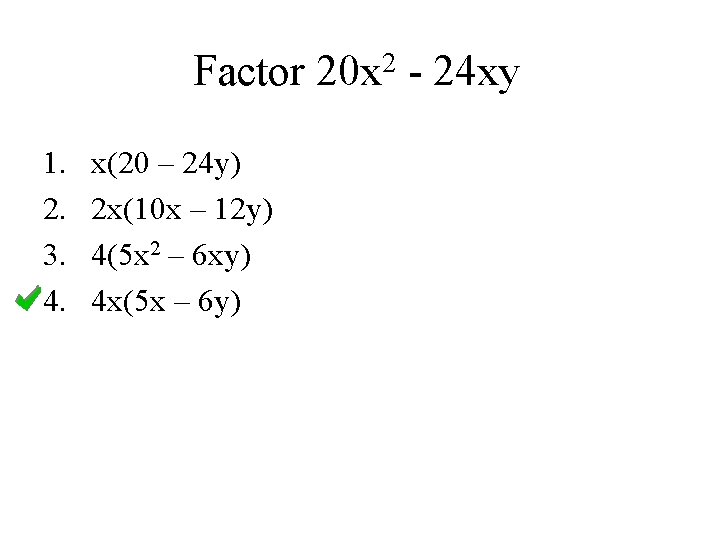
Factor 1. 2. 3. 4. x(20 – 24 y) 2 x(10 x – 12 y) 4(5 x 2 – 6 xy) 4 x(5 x – 6 y) 2 20 x - 24 xy

5) Factor 28 a 2 + 21 b - 35 b 2 c 2 GCF = 7 Divide each term by the GCF 4 a 2 + ___ 3 b - ____ 5 b 2 c 2 ) 28 a 2 + 21 b - 35 b 2 c 2 = 7 ( ___ Check your answer by distributing. 7(4 a 2 + 3 b – 5 b 2 c 2)
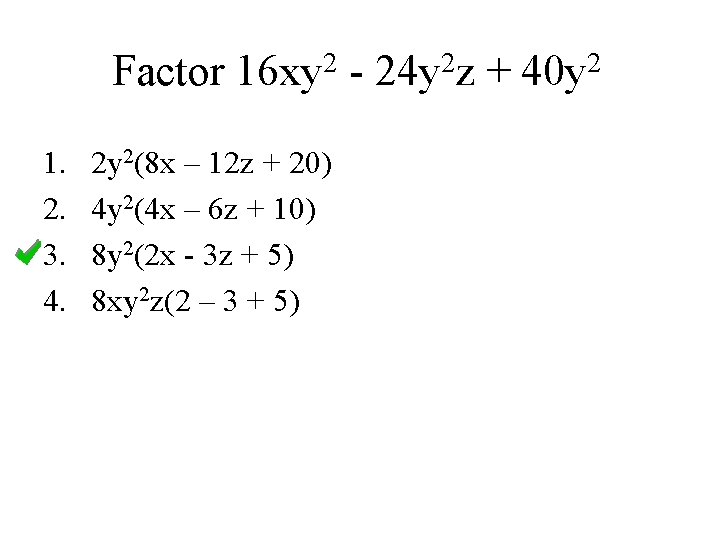
Factor 1. 2. 3. 4. 2 16 xy 2 y 2(8 x – 12 z + 20) 4 y 2(4 x – 6 z + 10) 8 y 2(2 x - 3 z + 5) 8 xy 2 z(2 – 3 + 5) - 2 24 y z + 2 40 y

Greatest Common Factors aka GCF’s Factor out the GCF for each polynomial: Factor out means you need the GCF times the remaining parts. a) b) c) d) e) 2 x + 4 y 5 a – 5 b 18 x – 6 y 2 m + 6 mn 5 x 2 y – 10 xy 2(x + 2 y) 5(a – b) How can you check? 6(3 x – y) 2 m(1 + 3 n) 5 xy(x - 2)
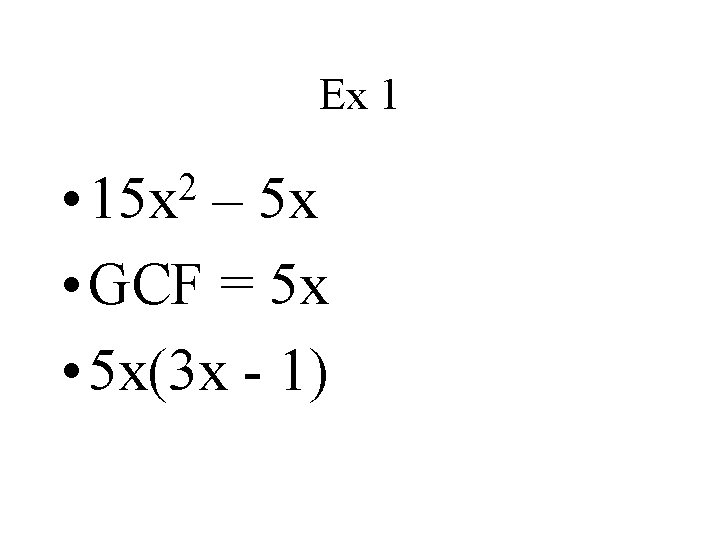
Ex 1 2 • 15 x – 5 x • GCF = 5 x • 5 x(3 x - 1)
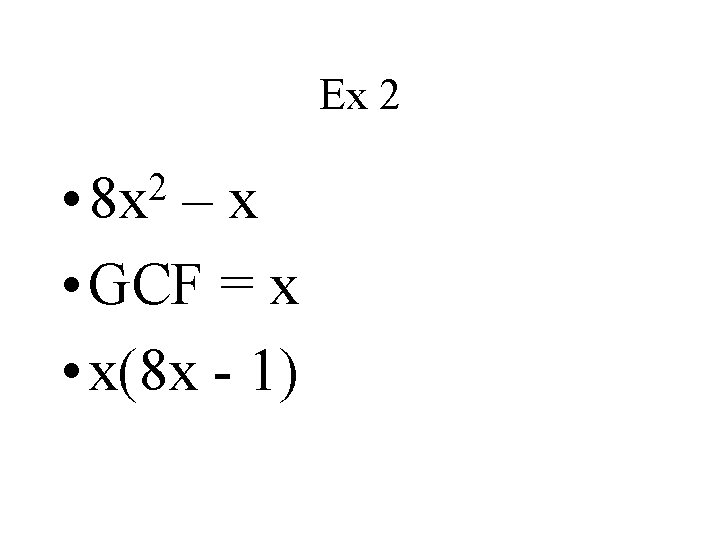
Ex 2 2 • 8 x –x • GCF = x • x(8 x - 1)
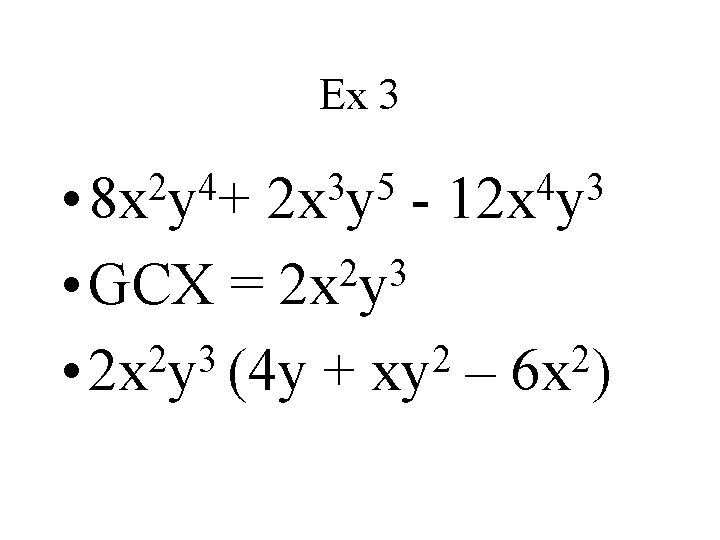
Ex 3 2 4 • 8 x y + 3 5 2 x y - 4 3 12 x y • GCX = 2 3 2 2 • 2 x y (4 y + xy – 6 x ) 2 3 2 x y

Method #2 • Difference of Two Squares 2 2 • a – b = (a + b)(a - b)

What is a Perfect Square • Any term you can take the square root evenly (No decimal) • 25 • 36 • 1 • x 2 • y 4

Difference of Perfect Squares x 2 – 4 the answer will look like this: ( = )( take the square root of each part: ( x 2)(x 2) Make 1 a plus and 1 a minus: (x + 2)(x - 2 ) )

FACTORING Difference of Perfect Squares EX: x 2 – 64 How: Solution: Take the square root of (x – 8)(x + 8) each part. One gets a + and one gets a -. Check answer by FOIL.
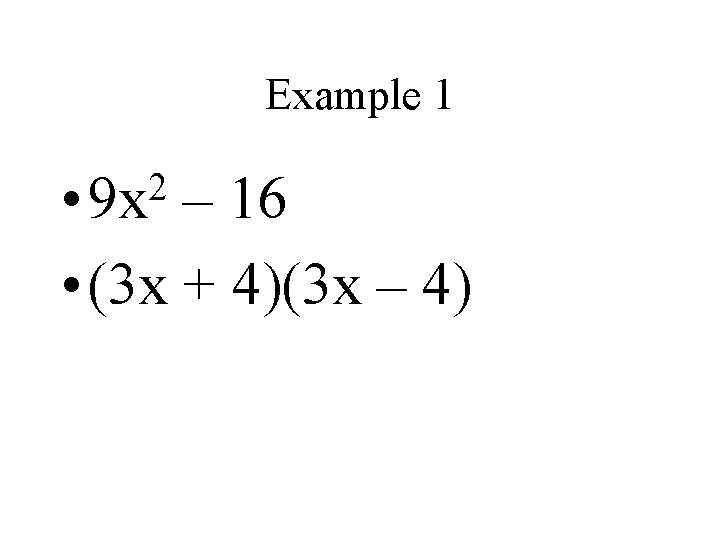
Example 1 2 • 9 x – 16 • (3 x + 4)(3 x – 4)
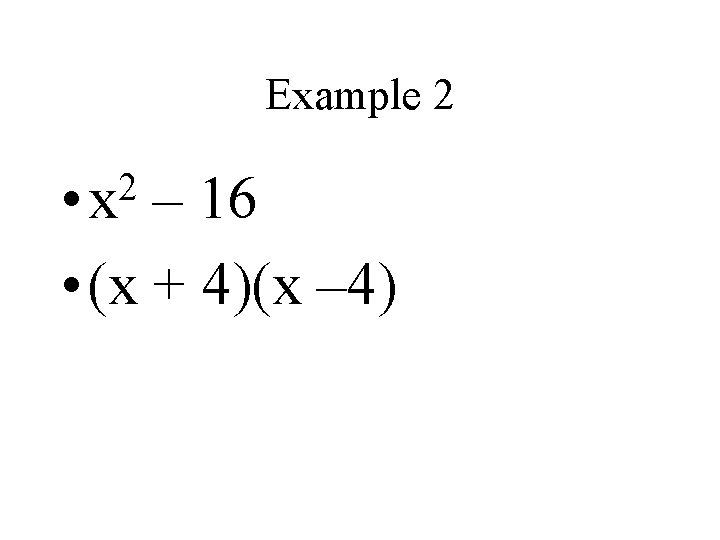
Example 2 2 • x – 16 • (x + 4)(x – 4)
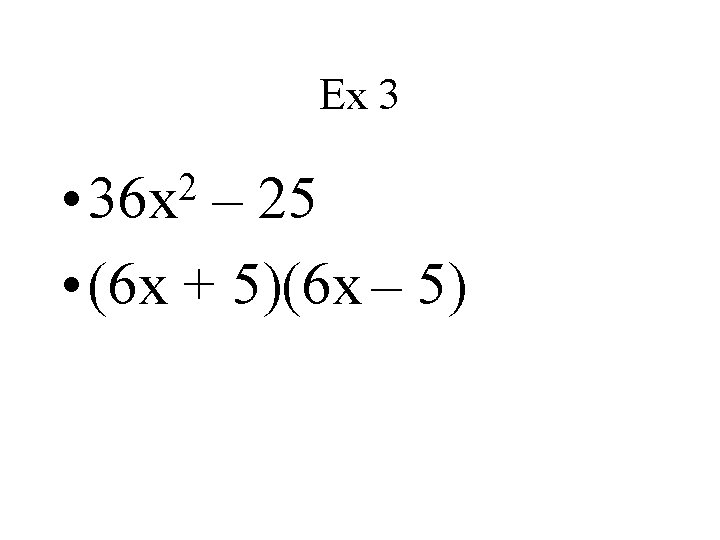
Ex 3 2 • 36 x – 25 • (6 x + 5)(6 x – 5)

More than ONE Method • It is very possible to use more than one factoring method in a problem • Remember: • ALWAYS use GCF first
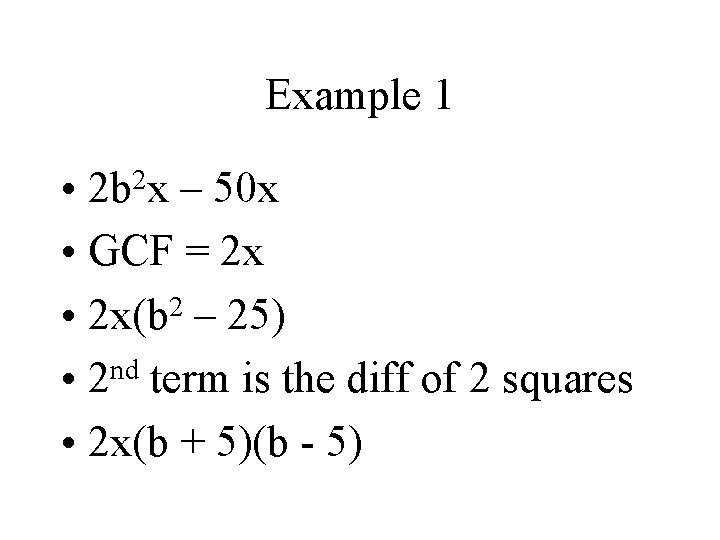
Example 1 • 2 b 2 x – 50 x • GCF = 2 x 2 • 2 x(b – 25) nd • 2 term is the diff of 2 squares • 2 x(b + 5)(b - 5)

Example 2 • • • 32 x 3 – 2 x GCF = 2 x 2 x(16 x 2 – 1) 2 nd term is the diff of 2 squares 2 x(4 x + 1)(4 x - 1)

ax 2 + bx + c

Example 1: x 2 + 11 x + 24 When factoring these trinomials the factors will be two binomials: (x + ) We know that the first terms of each binomial must be x because the first term of the trinomial is x 2 and x x = x 2. The challenge is to find the last term of each binomial. They must be chosen so that they will cause the coefficient of the middle term and the last term of the trinomial to work out. (That’s 11 and 24 in this case. ) Their sum equals the middle term of the trinomial. + = 11 Their product of those same numbers equals the last term of the trinomial. = 24

Example 1: x 2 + 11 x + 24 List the factors of 24: 1 24 SUM = 25 2 12 SUM = 14 3 8 SUM = 11 4 6 SUM = 10 It is the factors 3 and 8 that produce a sum of 11 AND a product of 24 so they must be the last terms of each binomial. (x + 3)(x + 8)

If we multiply these factors using FOIL, we get the polynomial that we started with. (x)(x) = x 2 (x + 3)(x + 8) = x 2 + 8 x + 3 x + 24 (x)(8) = 8 x (3)(x) = 3 x (3)(8) = 24 As we look at the 4 terms above, it becomes apparent why the sum of the last terms in each binomial must be equal to the middle term of the trinomial. (x + 3)(x + 8) = x 2 + 8 x + 3 x + 24 = x 2 + 11 x + 24

Example 2: a 2 + 16 a + 28 Factors of 28: 1 28 2 14 4 7 SUM = 16 a a = a 2 so they are the first terms of each binomial and the factors 2 and 14 make a sum of 16 so the are the last terms of each binomial. = (a + 2)(a + 14)

Example 3: y 2 + 2 y + 1 = (y + 1) Factors of 1: 1 1 SUM = 2 Sometimes there is only 1 pair of factors to consider. Factors of 1: Example 4: m 2 + 3 m + 1 1 1 SUM = 3 In this example the factors available do not make a sum of 3 which means that the Factors of 120: trinomial can’t be factored. 1 120 Example 5: p 2 + 23 p + 120 In this example there are many pairs of factors to consider. Most examples will have fewer than these. The trick is in being able to quickly find all of the factors of c. p 2 + 23 p + 120 = (p + 8)(p + 15) 2 60 3 40 4 30 5 24 6 20 8 15 10 12 SUM = 23

Example 6: x 2 + 5 x + 6 = (x + 2)(x + 3) Factors of 6: 1 6 2 3 SUM = 5 In each of the preceding examples the signs of the terms in the trinomials were always positive. Now we will observe examples where the signs can be negative. Example 7: x 2 + 5 x - 6 = (x - 1)(x + 6) Factors of -6: -1 +6 -2 +3 SUM = 5 When looking for the factors of a negative number, one must be positive and the other negative. If at the same time their sum is positive, then the factor that is bigger must be the positive one.

REVIEW OF RULES FOR SIGNS ADDITION MULTIPLICATION (+)(+) = (+) + (+) = (+)(-) = (-) (+) + (-) = Sign of bigger number (-)(+) = (-) + (+) = (-)(-) = (+) (-) + (-) = (-) ( ) Example 8: x 2 - 5 x - 6 = (x + 1)(x - 6) Factors of -6: When both the product and sum are negative, the factors have opposite signs but this time the bigger factor will be negative. +1 -6 +2 -3 SUM = -5

Example 9: x 2 - 5 x + 6 = (x - 2)(x - 3) Factors of 6: -1 -6 -2 -3 SUM = -5 When looking for factors of a positive number when the sum is negative, both factors will be negative. Example 10: x 2 - 5 x - 36 = (x + 4)(x - 9) Factors of -36: 1 -36 2 -18 3 -12 4 -9 6 -6 SUM = -5

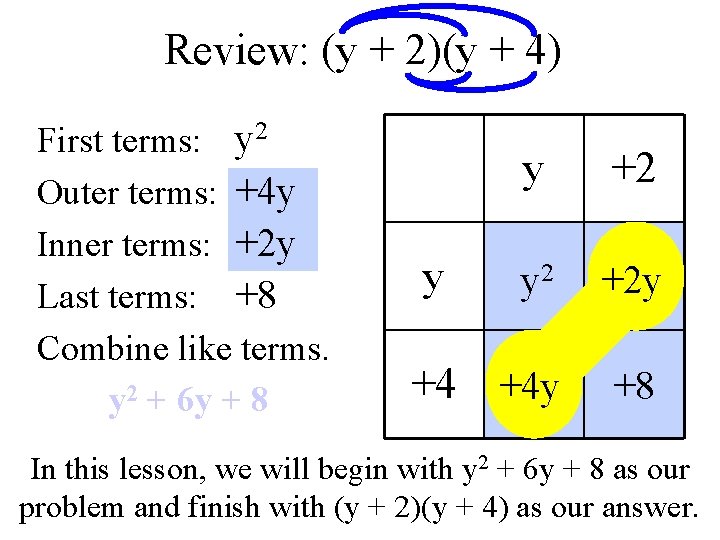
Review: (y + 2)(y + 4) y 2 +4 y +2 y +8 First terms: Outer terms: Inner terms: Last terms: Combine like terms. y 2 + 6 y + 8 y +2 y 2 +2 y +4 +4 y +8 y In this lesson, we will begin with y 2 + 6 y + 8 as our problem and finish with (y + 2)(y + 4) as our answer.

Here we go! 1) Factor y 2 + 6 y + 8 Use your factoring chart. Do we have a GCF? Nope! Is it a Diff. of Squares problem? No way! 3 terms! Now we will learn Trinomials! You will set up a table with the following information. Product of the first and last coefficients Middle coefficient The goal is to find two factors in the first column that add up to the middle term in the second column. We’ll work it out in the next few slides.

1) Factor 2 y M A + 6 y + 8 Create your MAMA table. Product of the first and last coefficients Multiply +8 Add +6 Middle coefficient Here’s your task… What numbers multiply to +8 and add to +6? If you cannot figure it out right away, write the combinations.

1) Factor 2 y + 6 y + 8 Place the factors in the table. Multiply +8 Which has a sum of +6? +1, +8 -1, -8 +2, +4 -2, -4 Add +6 +9, NO -9, NO +6, YES!! -6, NO We are going to use these numbers in the next step!

1) Factor y 2 + 6 y + 8 Multiply +8 Add +6 +2, +4 +6, YES!! Hang with me now! Replace the middle number of the trinomial with our working numbers from the MAMA table y 2 + 6 y + 8 y 2 + 2 y + 4 y + 8 Now, group the first two terms and the last two terms.

We have two groups! (y 2 + 2 y)(+4 y + 8) Almost done! Find the GCF of each group and factor it out. If things are done right, the parentheses y(y + 2) +4(y + 2) should be the same. Factor out the GCF’s. Write them in their own group. (y + 4)(y + 2) Tadaaa! There’s your answer…(y + 4)(y + 2) You can check it by multiplying. Piece of cake, huh? There is a shortcut for some problems too! (I’m not showing you that yet…)

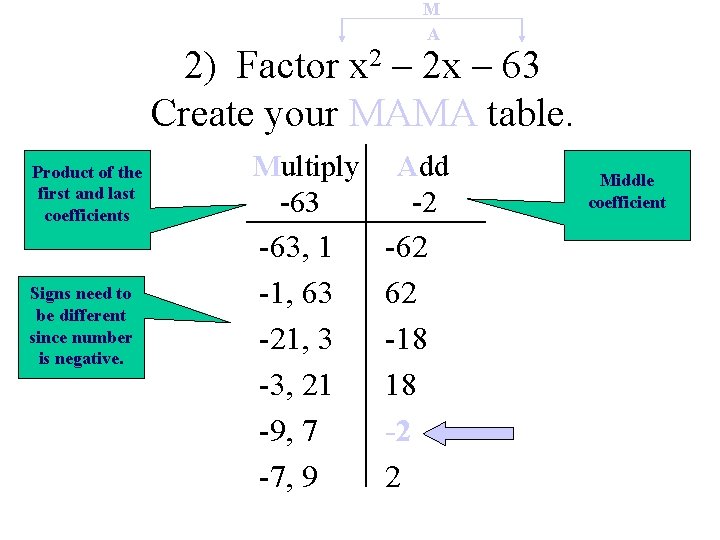
M A 2) Factor x 2 – 2 x – 63 Create your MAMA table. Product of the first and last coefficients Signs need to be different since number is negative. Multiply -63, 1 -1, 63 -21, 3 -3, 21 -9, 7 -7, 9 Add -2 -62 62 -18 18 -2 2 Middle coefficient

Replace the middle term with our working numbers. x 2 – 2 x – 63 x 2 – 9 x + 7 x – 63 Group the terms. (x 2 – 9 x) (+ 7 x – 63) Factor out the GCF x(x – 9) +7(x – 9) The parentheses are the same! Weeedoggie! (x + 7)(x – 9)

Here are some hints to help you choose your factors in the MAMA table. 1) When the last term is positive, the factors will have the same sign as the middle term. 2) When the last term is negative, the factors will have different signs.

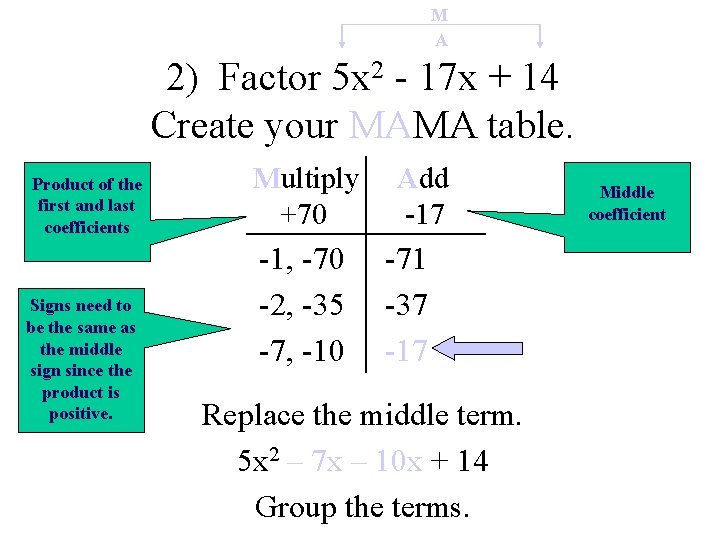
M A 2) Factor 5 x 2 - 17 x + 14 Create your MAMA table. Product of the first and last coefficients Signs need to be the same as the middle sign since the product is positive. Multiply +70 -1, -70 -2, -35 -7, -10 Add -17 -71 -37 -17 Replace the middle term. 5 x 2 – 7 x – 10 x + 14 Group the terms. Middle coefficient

(5 x 2 – 7 x) (– 10 x + 14) Factor out the GCF x(5 x – 7) -2(5 x – 7) The parentheses are the same! Weeedoggie! (x – 2)(5 x – 7) Hopefully, these will continue to get easier the more you do them.
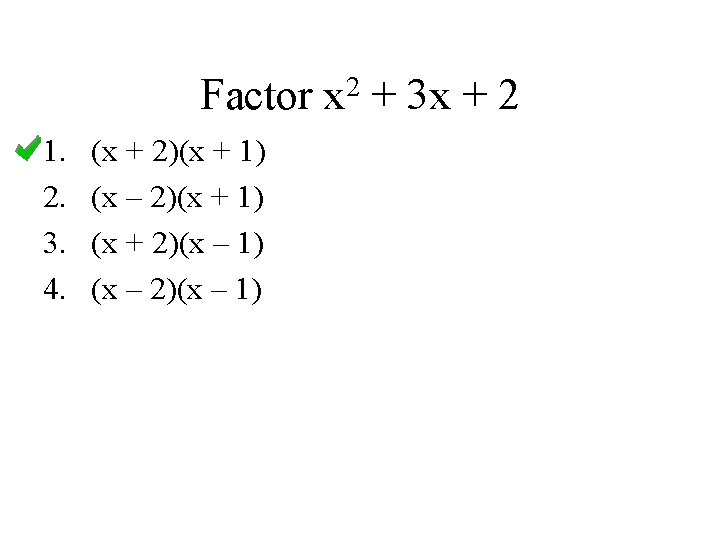
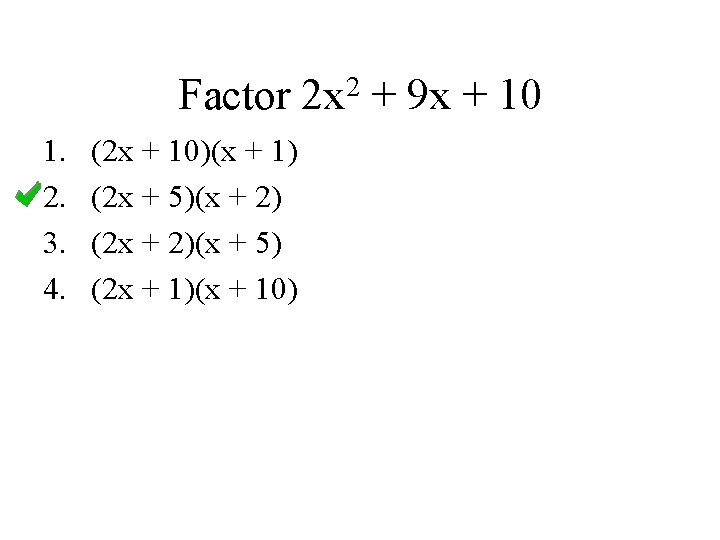
Factor 1. 2. 3. 4. (2 x + 10)(x + 1) (2 x + 5)(x + 2) (2 x + 2)(x + 5) (2 x + 1)(x + 10) 2 2 x + 9 x + 10
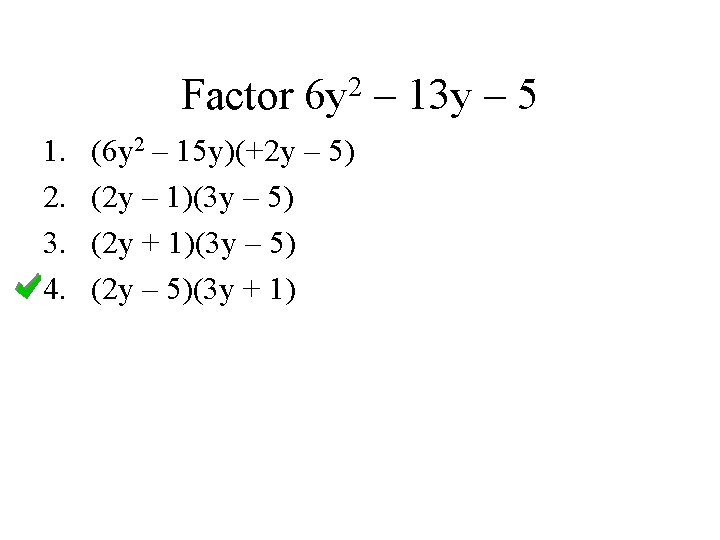
Factor 1. 2. 3. 4. 2 6 y (6 y 2 – 15 y)(+2 y – 5) (2 y – 1)(3 y – 5) (2 y + 1)(3 y – 5) (2 y – 5)(3 y + 1) – 13 y – 5

2) Factor 2 x 2 - 14 x + 12 Find the GCF! 2(x 2 – 7 x + 6) Now do the MAMA table! Signs need to be the same as the middle sign since the product is positive. Multiply +6 Add -7 -1, -6 -7 -2, -3 -5 Replace the middle term. 2[x 2 – x – 6 x + 6] Group the terms.
![2x 2 x 6 x 6 Factor out the GCF 2xx 2[(x 2 – x)(– 6 x + 6)] Factor out the GCF 2[x(x –](https://slidetodoc.com/presentation_image_h2/8f0e1fe752b2c41a5723f103a281d100/image-51.jpg)
2[(x 2 – x)(– 6 x + 6)] Factor out the GCF 2[x(x – 1) -6(x – 1)] The parentheses are the same! Weeedoggie! 2(x – 6)(x – 1) Don’t forget to follow your factoring chart when doing these problems. Always look for a GCF first!!