Elementrn funkce Zkladnmi elementrnmi funkcemi se nazvaj funkce

Elementární funkce • Základními elementárními funkcemi se nazývají funkce mocninné exponenciální logaritmické goniometrické cyklometrické • Elementárními funkcemi se nazývají funkce, které jsou vytvořeny ze základních elementárních funkcí pomocí konečného počtu základních algebraických operací (sčítání, odčítání, násobení, dělení, skládání). V rámci projektu „Cesta k vědě“ (veda. gymjs. net) vytvořil V. Pospíšil (vladimir. pospisil@fjfi. cvut. cz). Modifikace a šíření dokumentu podléhá licenci GNU ( www. gnu. org).

Rovnice • Rovnicí nazveme výraz (podmínku) ve tvaru. Všechna čísla x z definičního oboru funkce f, která podmínce vyhovují, nazveme řešením rovnice nebo kořeny funkce f. • Rovnici lze zapsat i ve tvaru. Na výchozí tvar ji lze převést odečtením g(x) od obou stran rovnosti : . Výraz nalevo je nová funkce. • Rovnice může mít obecně jedno nebo více řešení, popřípadě žádné či nekonečně mnoho – to záleží na tvaru funkce f(x). • Například rovnice má jedno řešení x = 1/2 má dvě řešení x = 2, x = -2 má nekonečně řešení x = 2 kπ, k Z nemá žádné řešení (v reálných číslech)

Polynomické funkce • Polynom n-tého stupně nazveme funkci ve tvaru kde koeficienty ai jsou obecně komplexní čísla, n přirozené číslo. • Pro některá n nazýváme polynomy konstantní, lineární, kvadratická a kubická funkce.

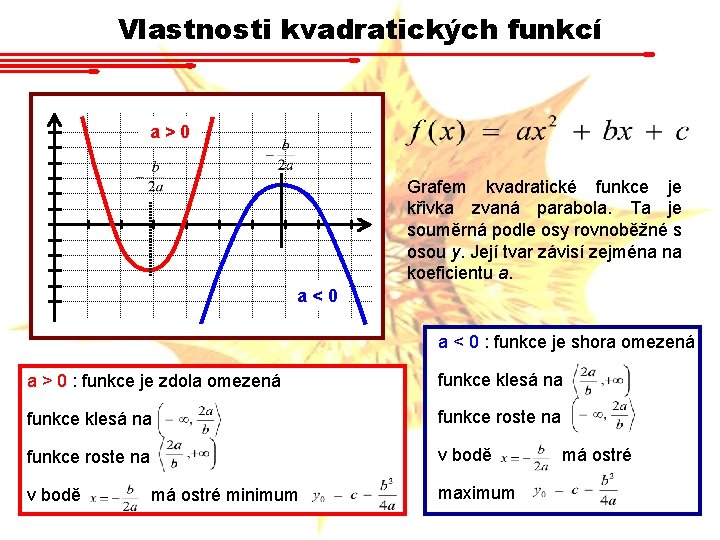
Vlastnosti kvadratických funkcí a>0 Grafem kvadratické funkce je křivka zvaná parabola. Ta je souměrná podle osy rovnoběžné s osou y. Její tvar závisí zejména na koeficientu a. a<0 a < 0 : funkce je shora omezená a > 0 : funkce je zdola omezená funkce klesá na funkce roste na v bodě má ostré minimum maximum má ostré

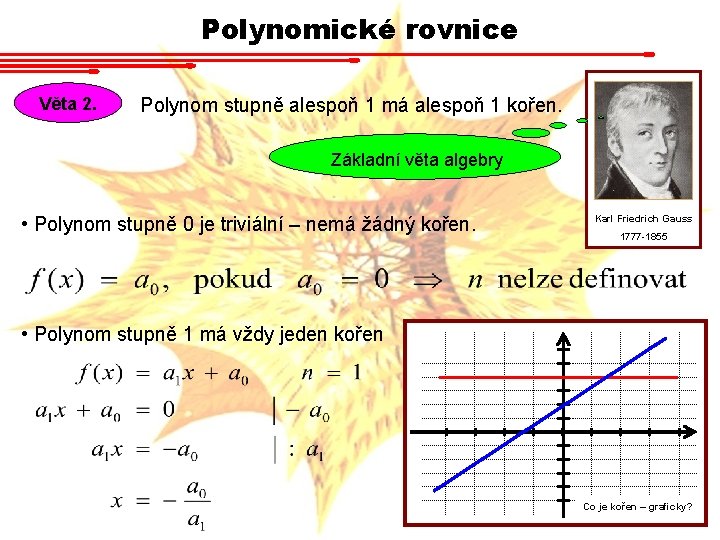
Polynomické rovnice Věta 2. Polynom stupně alespoň 1 má alespoň 1 kořen. Základní věta algebry • Polynom stupně 0 je triviální – nemá žádný kořen. Karl Friedrich Gauss 1777 -1855 • Polynom stupně 1 má vždy jeden kořen Co je kořen – graficky?

Polynomické rovnice • Polynom stupně 2 – musí mít alespoň jeden kořen? Má tento polynom alespoň jeden kořen? Ano, má dva : Základní věta algebry platí pouze v oboru komplexních čísel. V oboru reálných platit nemusí. Reálné kořeny rovnic jsou ale důležité. Jak spočítat obecně reálné kořeny kvadratické rovnice – či jak zjistit, že žádné nemá? Tuto rovnici lze řešit tzv. doplněním na úplný čtverec, tj. za využití vzorce

Řešení kvadratické rovnice Substituce p = b/a , q = c/a další výpočet zpřehlední. Nyní je nutné upravit výraz napravo tak, aby v něm bylo pouze jediné x. Využijeme předchozího vzorce jestliže vhodným doplněním členů získáme

Řešení kvadratické rovnice Přepsali jsme rovnici na tvar, ve kterém je již elementárními úpravami snadno k vyřešení: Nyní dosadíme zpět za p, q :

Řešení kvadratické rovnice Vzhledem k ± zde není nutné vkládat absolutní hodnotu.

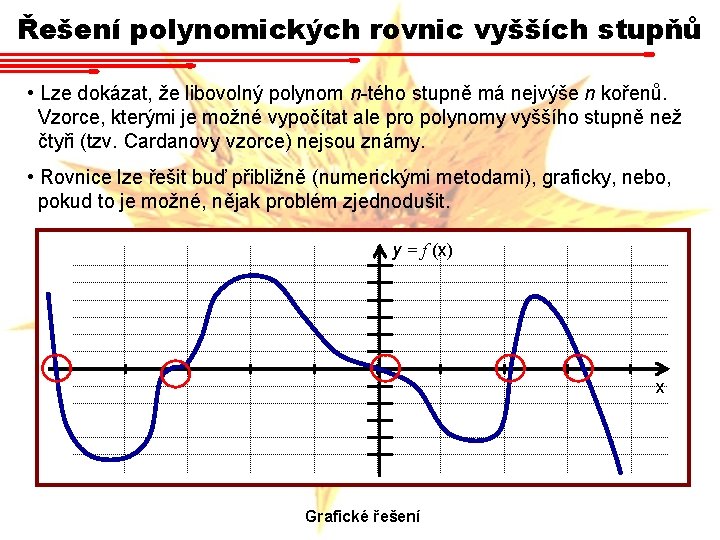
Řešení kvadratické rovnice • Tento vzorec ukazuje, že každý polynom druhého stupně má nejvýše dvě řešení. V reálném oboru lze o počtu kořenů rozhodnout z výrazu. Pokud , řešení je právě jedno. Je-li tento výraz záporný, rovnice reálné řešení nemá. Jinak má dvě. • Výraz D = b 2 - 4 ac nazýváme diskriminant. • Lze dokázat, že libovolný polynom n-tého stupně má nejvýše n kořenů. Vzorce, kterými je možné vypočítat ale pro polynomy vyššího stupně než čtyři (tzv. Cardanovy vzorce) nejsou známy. • Lze dokázat, že každý polynom lichého stupně s reálnými koeficienty má minimálně jeden reálný kořen.

Řešení polynomických rovnic vyšších stupňů • Lze dokázat, že libovolný polynom n-tého stupně má nejvýše n kořenů. Vzorce, kterými je možné vypočítat ale pro polynomy vyššího stupně než čtyři (tzv. Cardanovy vzorce) nejsou známy. • Rovnice lze řešit buď přibližně (numerickými metodami), graficky, nebo, pokud to je možné, nějak problém zjednodušit. y = f (x) x Grafické řešení

Řešení polynomických rovnic vyšších stupňů Příklad Vyřešte rovnici Řešení je triviální. Povšimneme si, že rovnici řeší x = 0. Předpokládáme-li, že x ≠ 0, pak můžeme celou rovnici x vydělit, zbude a dle dříve uvedeného vzorce pak x = 1, x = 2. Rovnice má tedy tři kořeny. • Obecně lze říci, že každý polynom lze zapsat jakoČísla k určují tzv. i násobnost kořenu. kde x 1 – xm jsou kořeny a ki přirozená čísla, pro která platí k 1 + k 2 +…+ km= n. Uhodneme-li nějakým způsobem jeden kořen, můžeme ho z polynomu „vytknout“ a celou rovnici vydělit příslušnou závorkou. Tím získáme polynomickou rovnici nižšího stupně.

Řešení polynomických rovnic vyšších stupňů Příklad Vyřešte rovnici Všimneme-li si například, že rovnici řeší x = 3, pak snadno dospějeme k následujícímu: Rovnice má tedy dva kořeny, x = 3, x = 1. Druhý z kořenů má násobnost 2.

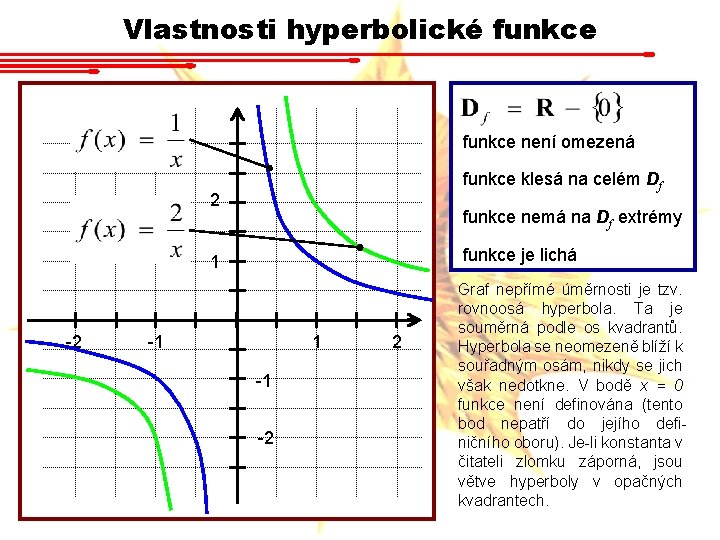
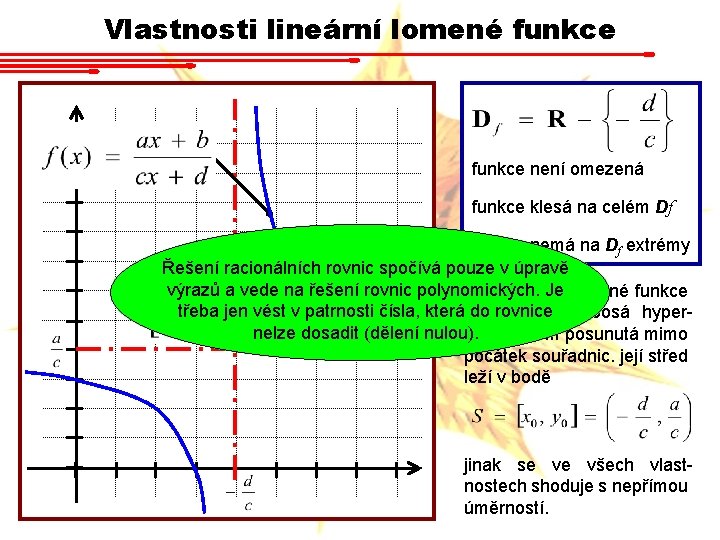
Racionální funkce • Racionální nazveme funkci ve tvaru kde koeficienty pi, qj jsou obecně komplexní čísla, n a m přirozená čísla. Jedná se zjevně o podíl dvou polynomů. • Ve speciálních případech nazýváme funkce hyperbolická (nepřímá úměrnost) a lineární lomená funkce. Podmínky u druhé z funkcí zajišťují, aby se z výrazu nestala funkce lineární či dokonce konstantní.

Vlastnosti hyperbolické funkce není omezená funkce klesá na celém Df 2 funkce nemá na Df extrémy funkce je lichá 1 -2 -1 1 -1 -2 2 Graf nepřímé úměrnosti je tzv. rovnoosá hyperbola. Ta je souměrná podle os kvadrantů. Hyperbola se neomezeně blíží k souřadným osám, nikdy se jich však nedotkne. V bodě x = 0 funkce není definována (tento bod nepatří do jejího definičního oboru). Je-li konstanta v čitateli zlomku záporná, jsou větve hyperboly v opačných kvadrantech.

Vlastnosti lineární lomené funkce není omezená funkce klesá na celém Df funkce nemá na Df extrémy Řešení racionálních rovnic spočívá pouze v úpravě výrazů a vede na řešení rovnic polynomických. Je lomené funkce Graf lineární třeba jen vést v patrnosti čísla, kterájedorovněž rovnice rovnoosá hypernelze dosadit (dělení nulou). bola, ovšem posunutá mimo počátek souřadnic. její střed leží v bodě jinak se ve všech vlastnostech shoduje s nepřímou úměrností.

Exponenciální funkce • Exponenciální funkcí o základu a nazveme funkci Podmínky jsou nutné, neboť reálná mocnina je definována pouze pro kladná čísla a v případě, že a = 1, není funkce exponenciální, nýbrž polynomická 0. stupně. • Pro vědeckou praxi jsou důležité exponenciální funkce se základy dekadická exp. funkce přirozená exp. funkce Iracionální číslo e se nazývá eulerovo, nebo základ přirozeného logaritmu. Dostaneme se k němu v rámci úvodu do matematické analýzy.

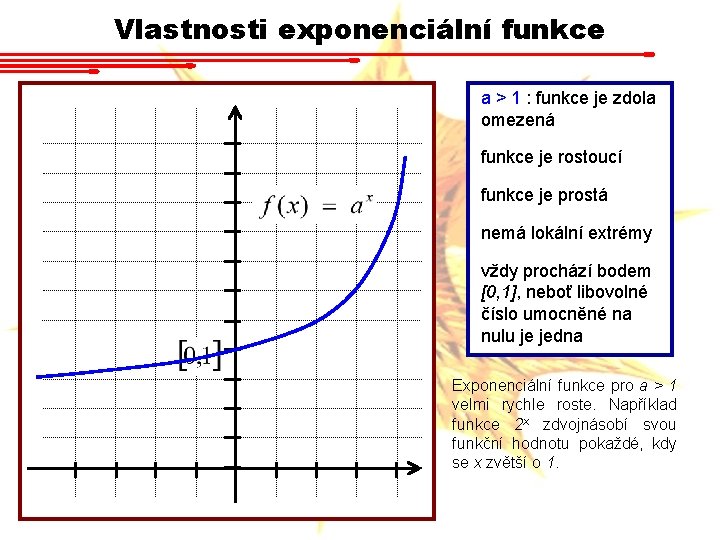
Vlastnosti exponenciální funkce a > 1 : funkce je zdola omezená funkce je rostoucí funkce je prostá nemá lokální extrémy vždy prochází bodem [0, 1], neboť libovolné číslo umocněné na nulu je jedna Exponenciální funkce pro a > 1 velmi rychle roste. Například funkce 2 x zdvojnásobí svou funkční hodnotu pokaždé, kdy se x zvětší o 1.

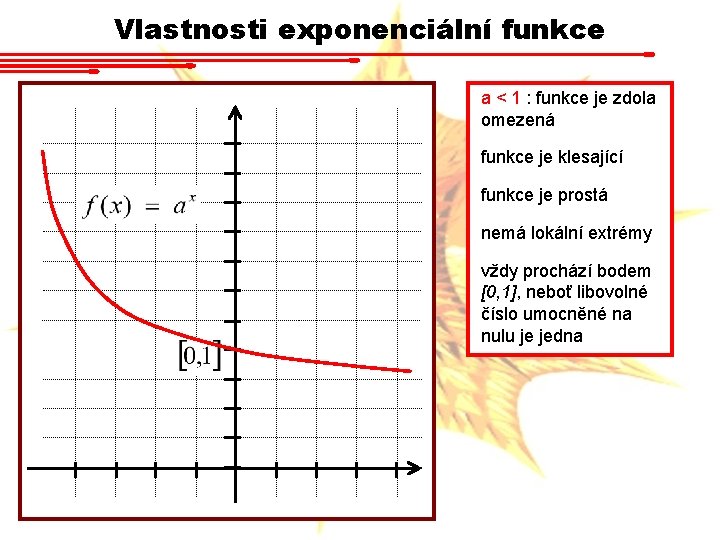
Vlastnosti exponenciální funkce a < 1 : funkce je zdola omezená funkce je klesající funkce je prostá nemá lokální extrémy vždy prochází bodem [0, 1], neboť libovolné číslo umocněné na nulu je jedna

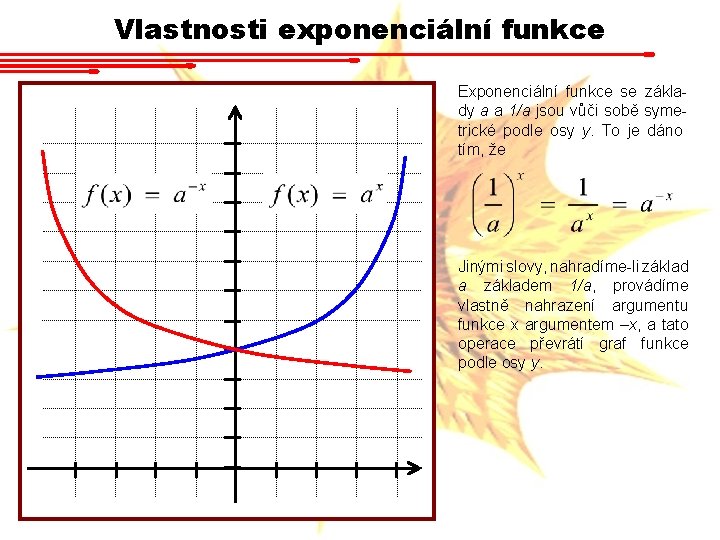
Vlastnosti exponenciální funkce Exponenciální funkce se základy a a 1/a jsou vůči sobě symetrické podle osy y. To je dáno tím, že Jinými slovy, nahradíme-li základ a základem 1/a, provádíme vlastně nahrazení argumentu funkce x argumentem –x, a tato operace převrátí graf funkce podle osy y.

Logaritmické funkce • Logaritmickou funkcí o základu a nazveme funkci inverzní k zapisujeme • Jelikož exponenciální funkce je prostá v celém svém definičním oboru, je možné k ní utvořit funkci inverzní na celém oboru hodnot. Obor hodnot exponenciální funkce je ovšem interval (0, +∞), proto je tento interval zároveň definičním oborem logaritmu. Dle definice platí • Pro zjednodušení se zavádí zápisy

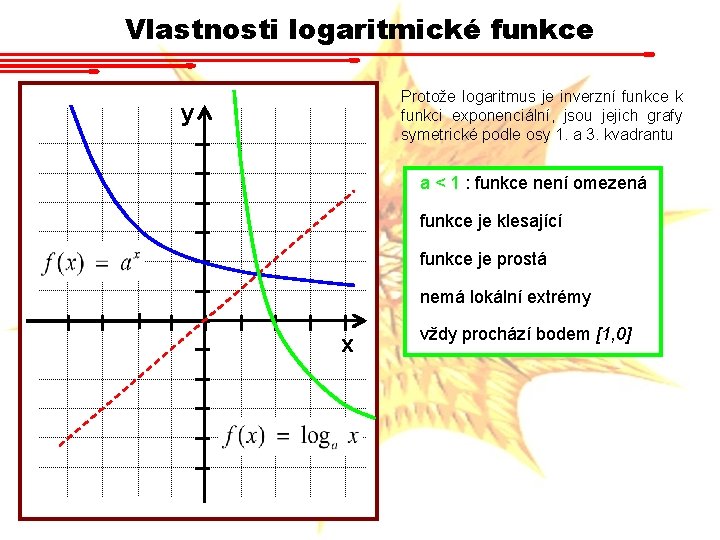
Vlastnosti logaritmické funkce Protože logaritmus je inverzní funkce k funkci exponenciální, jsou jejich grafy symetrické podle osy 1. a 3. kvadrantu y a > 1 : funkce není omezená funkce je rostoucí funkce je prostá nemá lokální extrémy x vždy prochází bodem [1, 0]

Vlastnosti logaritmické funkce Protože logaritmus je inverzní funkce k funkci exponenciální, jsou jejich grafy symetrické podle osy 1. a 3. kvadrantu y a < 1 : funkce není omezená funkce je klesající funkce je prostá nemá lokální extrémy x vždy prochází bodem [1, 0]

Vlastnosti exponentů a logaritmů Tato identita plyne přímo z definice. Logaritmus a exponenciála jsou k sobě navzájem inverzní. Zapíšeme-li tedy exponenciálu jako inverzní funkci k logaritmu a neprohodíme x a y, získáme Z definice rovněž plyne

Vlastnosti exponentů a logaritmů Dále platí pro libovolná x 1, x 2 > 0, a ≠ 1 : Rovnosti vycházejí z vlastnosti exponenciál Poslední rovnost je splněna pouze v tom případě, že se rovnají výrazy v exponentu.

Vlastnosti exponentů a logaritmů Předchozí rovnosti lze rozšířit na Dále platí pro libovolná x > 0, a ≠ 1, r reálná a n přirozená : Což by šlo dokázat stejně jako předchozí identity. Odsud také rovnou plyne

Vlastnosti exponentů a logaritmů Poslední důležitý vztah pro logaritmy je To vyplývá z následujících jednoduchých úprav: celá rovnost zlogaritmována při základu b Speciálně pak

Příklady na počítání s logaritmy

Příklady na počítání s logaritmy Pomocí logaritmů lze převést řadu násobení a dělení na sčítání a odčítání. Dříve se tohoto faktu hojně využívalo při výpočtech za pomoci logaritmického pravítka. logaritmické stupnice

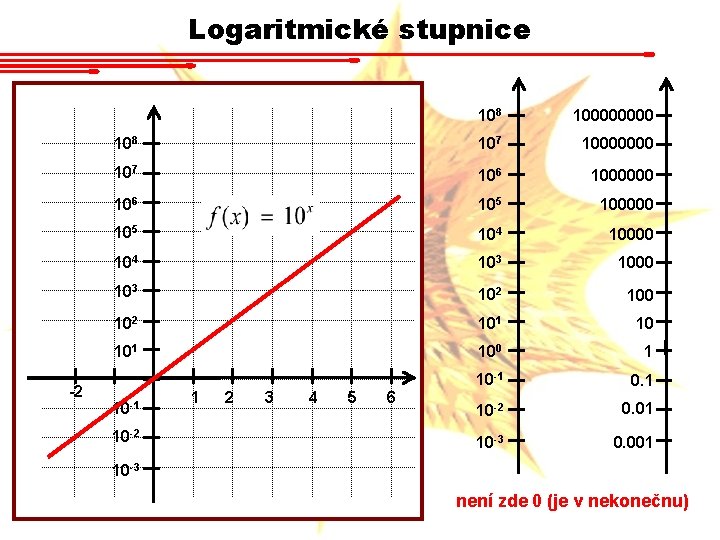
Logaritmické stupnice -2 108 10000 108 107 10000000 107 106 1000000 106 105 100000 105 104 10000 104 103 1000 103 102 100 102 101 100 1 10 -1 0. 1 10 -2 0. 01 10 -3 0. 001 10 -2 1 2 3 4 5 6 10 -3 není zde 0 (je v nekonečnu)

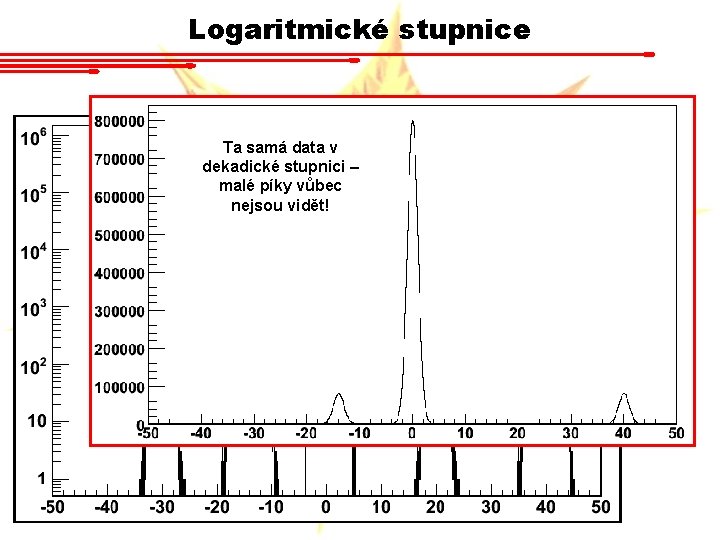
Logaritmické stupnice Ta samá data v dekadické stupnici – malé píky vůbec nejsou vidět!

Logaritmické stupnice

Exponenciální a logaritmické rovnice • Exponenciální rovnicí nazveme každou rovnost, ve které se neznámá vyskytuje v exponentu. Základní tvar takové rovnice lze zapsat jako kde f(x) a g(x) jsou nějaké jednodušší funkce (např. racionální). Z tohoto tvaru lze rovnici převést na racionální zlogaritmováním s libovolným základem, např. 10: Výrazy log a a log b jsou pro danou rovnici konstanty a lze je najít v tabulkách či spočítat na kalkulačce.

Exponenciální a logaritmické rovnice Příklad Vyřešte rovnici Protože platí, že lze rovnici upravit na K řešení jsme využili faktu, že po elementární úpravě byly obě funkce v exponentu stejné. Nebylo tedy nutné celou rovnici zlogaritmovat.

Exponenciální a logaritmické rovnice Příklad Vyřešte rovnici Rovnici upravíme : a zlogaritmujeme:

Exponenciální a logaritmické rovnice Příklad Vyřešte rovnici Součty nelze zlogaritmovat a mocniny mají různé základy. Je třeba rovnici nejprve nějak upravit:

Exponenciální a logaritmické rovnice Příklad Vyřešte rovnici

Exponenciální a logaritmické rovnice • Logaritmickou rovnicí nazveme každou rovnost, ve které se neznámá vyskytuje argumentu logaritmu. Základní tvar takové rovnice lze zapsat jako kde f(x) a g(x) jsou nějaké jednodušší funkce (např. racionální). Z tohoto tvaru lze rovnici převést na racionální převodem na společný základ a odlogaritmováním: Většinou se ovšem setkáváme z jednoduššími rovnicemi, u kterých je základní tvar

Exponenciální a logaritmické rovnice Příklad Vyřešte rovnici

Exponenciální a logaritmické rovnice Příklad Vyřešte rovnici Je třeba mít na pamětí, že argumenty logaritmů musí být kladné a tedy x > -3 a zároveň x > 2, tedy dohromady x > 2. Vyjde-li nám jiný výsledek, musíme jej zahodit.

Shrnutí • Elementární funkce • Rovnice, kořeny rovnice • Polynomy, polynomické rovnice, základní věta algebry • Kvadratická funkce a rovnice • Řešení polynomických rovnic vyšších stupňů • Racionální funkce • Nepřímá úměrnost, lineární lomená funkce • Exponenciální a logaritmické funkce • Vlastnosti exponenciál a logaritmů, logaritmická stupnice • Exponenciální a logaritmické rovnice