Dynamic Programming Introduction Quy hoch ng l Thng

Dynamic Programming

Introduction Quy hoạch động: l Thường dùng để giải các bài toán tối ưu; l Phân rã bài toán thành các bài toán con; hình thành lời giải từ các bài toán con; l Lưu trữ lời giải các bài toán con trong một bảng dữ liệu thay cho giải lại các bài toán con (đệ quy). Đặc điểm của phương pháp chia để trị: • Thường phát sinh các bài toán con “mới” • Lời giải các bài toán con thường được sử dụng nhiều lần (“phủ chồng”). 2021 -03 -06 Dao Thanh Tinh 2

Introduction (2) Ví dụ 1: Tính số Fibonacci thứ n với f 0=0 và f 1 = 1 Theo công thức: Dùng mảng: f[0] = 0; f[1]=1; for (i=2; i n; i++) f[i] = f[i-1] + f[i-2]; output f[n]; 2021 -03 -06 Đệ quy: long f(int m) { if (n==0) return 0; else if (n==1) return 1; else return f(n-1) + f(n); } Ví dụ, để tính f(n) phải tính f(2) n-1 lần! Tiết kiệm bộ nhớ: f 0 = 0; f 1=1; for (i=2; i n; i++) { tg = f 1 + f 0; f 0 = f 1; f 1 = tg; } output f 1; Dao Thanh Tinh 3

Introduction (3) Số Fibonacci thứ n n=50 F(n) Phương pháp đệ quy Các phương pháp khác 2021 -03 -06 =12, 586, 269, 025 650 800 s 1 s Dao Thanh Tinh 4

Introduction (4) Tiếp cận theo hướng bottom-up 2021 -03 -06 1. Xuất phát từ những bài toán cơ sở có lời giải (cách giải đơn giản hoặc có sẵn) 2. Từ tập lời giải các bài toán con tìm lời giải của bài toán lớn hơn. Dao Thanh Tinh 5

Introduction (5) PRINCIPLE OF OPTIMALITY “An optimal policy has the property that whatever the initial state and initial decisions are, the remaining decisions must constitute an optimal policy with regard to the state resulting from the first decisions. ” Richard Bellman “The Theory of Dynamic Programming”, Bulletin of the American Mathematical Society, Vol. 60, No. 6, 1954 (503 -515). 2021 -03 -06 Dao Thanh Tinh 6

Introduction (6) Một chiến lược tối ưu có đặc trưng: với mọi trạng thái khởi tạo và quyết định ban đầu, các quyết định tiếp theo phải thiết lập được chiến lược tối ưu đối với trạng thái được hình thành từ các quyết định trước đó. Chiến lược tối ưu: có thể trong một số bước đầu tiên lựa chọn dường như không tốt nhưng tổng hợp cả quá trình phải tốt nhất. 2021 -03 -06 Dao Thanh Tinh 7

Introduction (7) Kỹ thuật giải bài toán bằng phương pháp QHĐ: 2021 -03 -06 Dao Thanh Tinh 8

Introduction (8) Ví dụ 2: Xét bài toán: Cho túi T có sức chứa 10 kg và 3 đồ vật: 1) 5 kg, trị giá 4$ 2) 4 kg, trị giá 10$ 3) 6 kg, trị giá 3$ Xếp những đồ vật nào vào túi để có giá trị lớn nhất? 2021 -03 -06 Dao Thanh Tinh 9

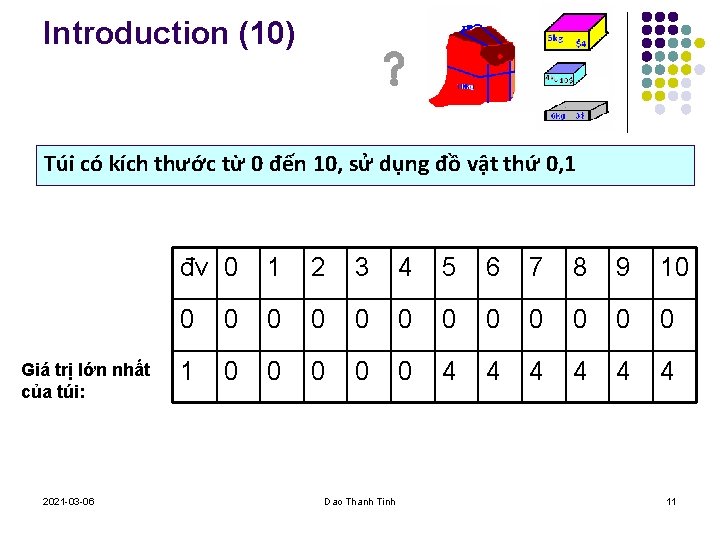
Introduction (9) Túi có kích thước từ 0 đến 10, sử dụng đồ vật thứ 0!!!! Giá trị lớn nhất của túi: 2021 -03 -06 đv 0 1 2 3 4 5 6 7 8 9 10 0 0 0 Dao Thanh Tinh 10

Introduction (10) Túi có kích thước từ 0 đến 10, sử dụng đồ vật thứ 0, 1 Giá trị lớn nhất của túi: 2021 -03 -06 đv 0 1 2 3 4 5 6 7 8 9 10 0 0 0 1 0 0 0 4 4 4 Dao Thanh Tinh 11

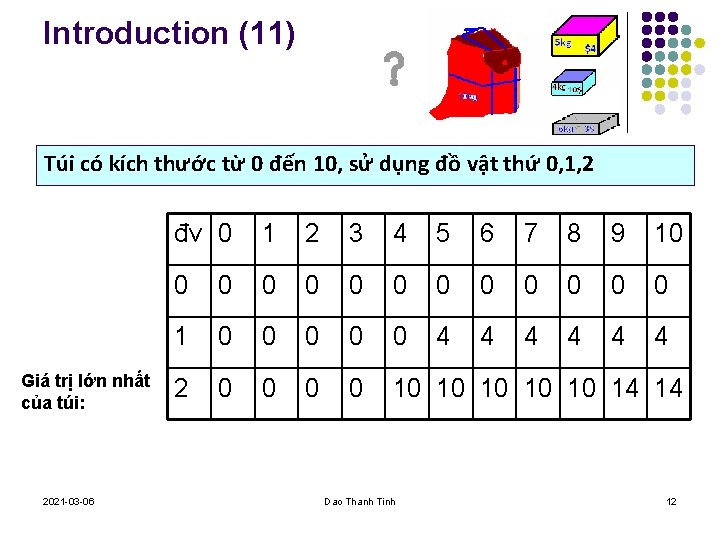
Introduction (11) Túi có kích thước từ 0 đến 10, sử dụng đồ vật thứ 0, 1, 2 Giá trị lớn nhất của túi: 2021 -03 -06 đv 0 1 2 3 4 5 6 7 8 9 10 0 0 0 1 0 0 0 4 4 4 2 0 0 10 10 10 14 14 Dao Thanh Tinh 12

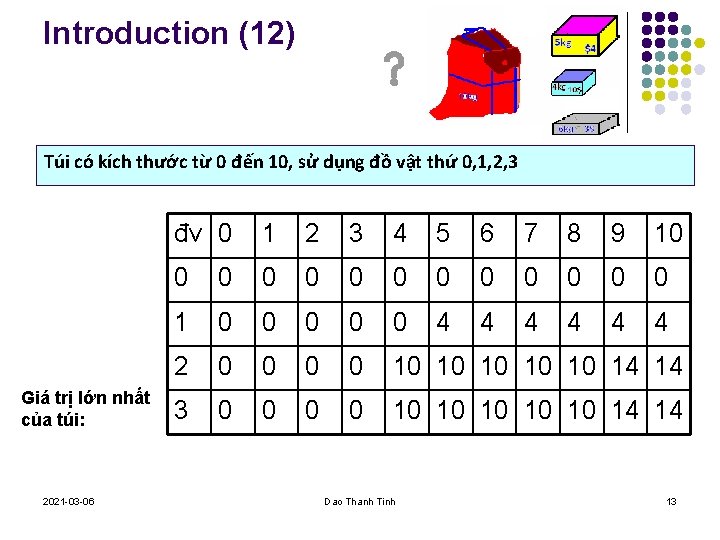
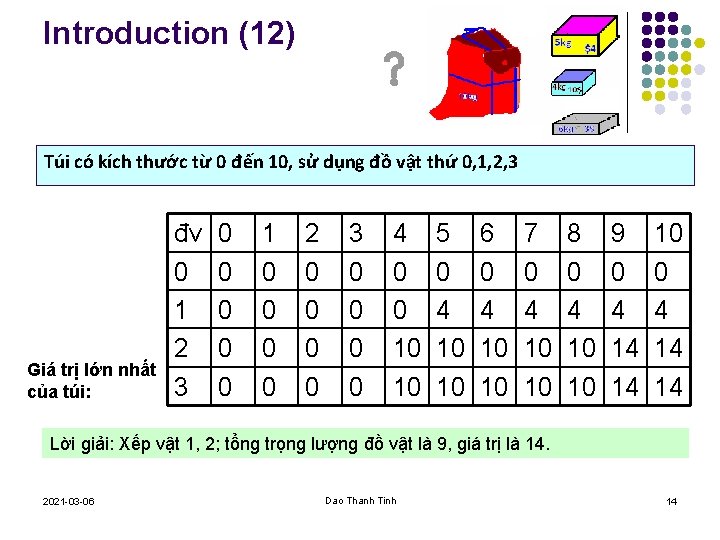
Introduction (12) Túi có kích thước từ 0 đến 10, sử dụng đồ vật thứ 0, 1, 2, 3 Giá trị lớn nhất của túi: 2021 -03 -06 đv 0 1 2 3 4 5 6 7 8 9 10 0 0 0 1 0 0 0 4 4 4 2 0 0 10 10 10 14 14 3 0 0 10 10 10 14 14 Dao Thanh Tinh 13

Introduction (12) Túi có kích thước từ 0 đến 10, sử dụng đồ vật thứ 0, 1, 2, 3 Giá trị lớn nhất của túi: đv 0 1 2 3 0 0 0 1 0 0 2 0 0 3 0 0 4 0 0 10 10 5 0 4 10 10 6 0 4 10 10 7 0 4 10 10 8 0 4 10 10 9 0 4 14 14 10 0 4 14 14 Lời giải: Xếp vật 1, 2; tổng trọng lượng đồ vật là 9, giá trị là 14. 2021 -03 -06 Dao Thanh Tinh 14

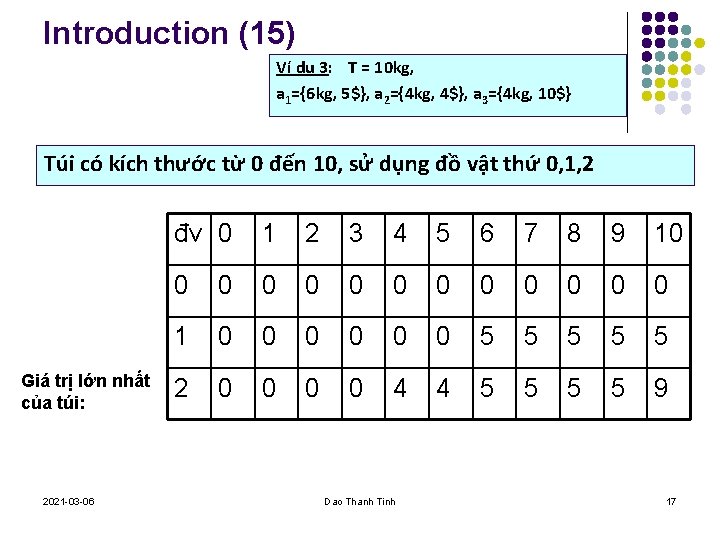
Introduction (13) Ví dụ 3: T = 10 kg, a 1={6 kg, 5$}, a 2={4 kg, 4$}, a 3={4 kg, 10$} Túi có kích thước từ 0 đến 10, sử dụng đồ vật thứ 0!!!! Giá trị lớn nhất của túi: 2021 -03 -06 đv 0 1 2 3 4 5 6 7 8 9 10 0 0 0 Dao Thanh Tinh 15

Introduction (14) Ví dụ 3: T = 10 kg, a 1={6 kg, 5$}, a 2={4 kg, 4$}, a 3={4 kg, 10$} Túi có kích thước từ 0 đến 10, sử dụng đồ vật thứ 0, 1 Giá trị lớn nhất của túi: 2021 -03 -06 đv 0 1 2 3 4 5 6 7 8 9 10 0 0 0 1 0 0 0 5 5 5 Dao Thanh Tinh 16

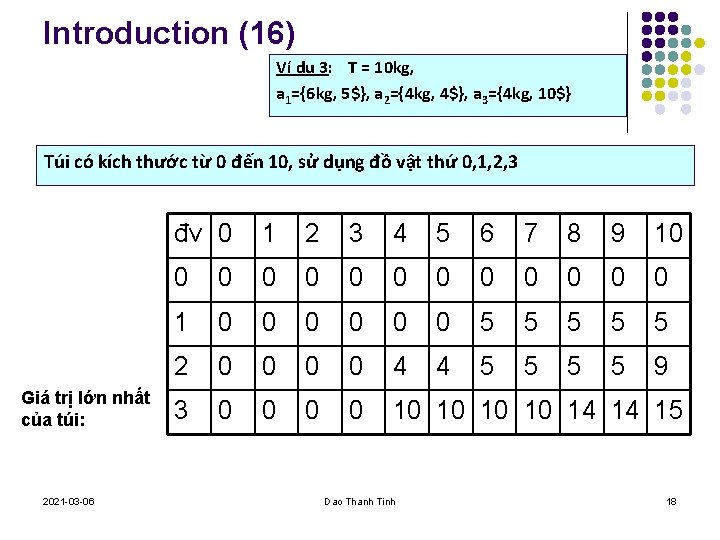
Introduction (15) Ví dụ 3: T = 10 kg, a 1={6 kg, 5$}, a 2={4 kg, 4$}, a 3={4 kg, 10$} Túi có kích thước từ 0 đến 10, sử dụng đồ vật thứ 0, 1, 2 Giá trị lớn nhất của túi: 2021 -03 -06 đv 0 1 2 3 4 5 6 7 8 9 10 0 0 0 1 0 0 0 5 5 5 2 0 0 4 4 5 5 9 Dao Thanh Tinh 17

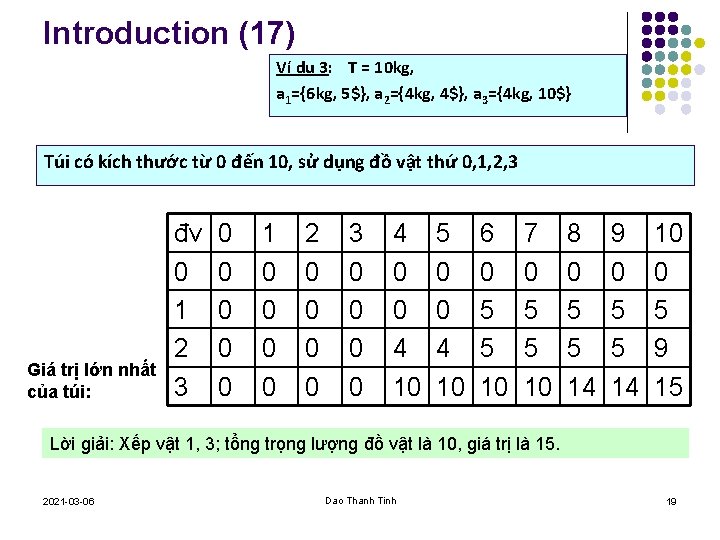
Introduction (16) Ví dụ 3: T = 10 kg, a 1={6 kg, 5$}, a 2={4 kg, 4$}, a 3={4 kg, 10$} Túi có kích thước từ 0 đến 10, sử dụng đồ vật thứ 0, 1, 2, 3 Giá trị lớn nhất của túi: 2021 -03 -06 đv 0 1 2 3 4 5 6 7 8 9 10 0 0 0 1 0 0 0 5 5 5 2 0 0 4 4 5 5 9 3 0 0 10 10 14 14 15 Dao Thanh Tinh 18

Introduction (17) Ví dụ 3: T = 10 kg, a 1={6 kg, 5$}, a 2={4 kg, 4$}, a 3={4 kg, 10$} Túi có kích thước từ 0 đến 10, sử dụng đồ vật thứ 0, 1, 2, 3 Giá trị lớn nhất của túi: đv 0 1 2 3 0 0 0 1 0 0 2 0 0 3 0 0 4 10 5 0 0 4 10 6 0 5 5 10 7 0 5 5 10 8 0 5 5 14 9 0 5 5 14 10 0 5 9 15 Lời giải: Xếp vật 1, 3; tổng trọng lượng đồ vật là 10, giá trị là 15. 2021 -03 -06 Dao Thanh Tinh 19

Introduction (18) Example 1. An Allocation Problem. Giả thiết x>0 là giá trị đầu tư ở thời điểm ban đầu. Chia x thành 2 phần: y 0 và x-y 0 Khai thác: phần thứ nhất mang lại g(y), giá trị còn lại là ay, 0<a<1; phần thứ hai mang lại h(x-y), giá trị còn lại là b(x-y), 0<b<1; Quá trình khai thác tiếp tục với ay+b(x-y) cho đến khi có thể kết thúc. Hỏi, ở mỗi bước cần phân chia như thế nào để đạt giá trị lớn nhất. Kí hiệu f(x) là giá trị thu được khi khai thác tốt nhất lượng đầu tư x ban đầu f(x) = sup {g(y) + h(x - y) + f (ay + b(x - y)) }, 0 y x, f(0) = 0 2021 -03 -06 Dao Thanh Tinh 20

Introduction (19) Example 2. Stochastic Gold Mining Giả thiết: 2 mỏ vàng A, B và một máy khai thác vàng rất nhạy: Nếu khai thác ở mỏ A: xác suất p là khai phá được r% lượng quặng máy vẫn chưa hỏng, xác suất (1 -p) là không được gì và máy hỏng. Sử dụng ở mỏ B: s% với xác suất q và máy không bị hỏng, xác suất (1 -q) không tìm được vàng và hỏng máy. Ở mỗi giai đoạn, chừng nào máy chưa hỏng có thể chọn khai thác ở mỏ A hay B. Cho trước lượng quặng x và y ở mỏ A và B tương ứng. Chọn trình tự khai thác tối ưu. Ký hiệu f(x, y) là lượng quặng đào được tối đa trước khi máy bị hỏng. Hiệu quả khai thác ở mỏ A: p(rx + f((1 r)x, y)) Hiệu quả khai thác ở mỏ B: q(sy + f(x, (1 s)y)) f(x, y) = rx + f((1 r)x, y), if p[rx + f((1 r)x, y)] q[sy + f(x, (1 s)y)] =sy + f(x, (1 s)y), othewise 2021 -03 -06 Dao Thanh Tinh 21

Matrix Multiplication Problem Suppose given matrices A 1, A 2, . . . , An, where the dimensions of Ai is di-1 di How should compute A 1 A 2. . . An What is the minimum number of element-wise multiplications? 2021 -03 -06 Dao Thanh Tinh 22

Matrix Multiplication (2) Cho A kích thước B kích thước C = A B Tính m n n p C(i, j) = A(i, 1)*B(1, j) + A(I, 2)*B(2, j) +…+ A(I, n)*B(n, j) i = 1, . . m, j = 1, . . p Số phép nhân: m n p A B C Example 1 40 1 1 40 40 10 A(BC) 40 1 1 10 40. 1. 10 + 1. 40. 10 = 800 (AB)C 40 40 40 10 40. 1. 40 + 40. 10 = 32, 000 2021 -03 -06 Dao Thanh Tinh 23

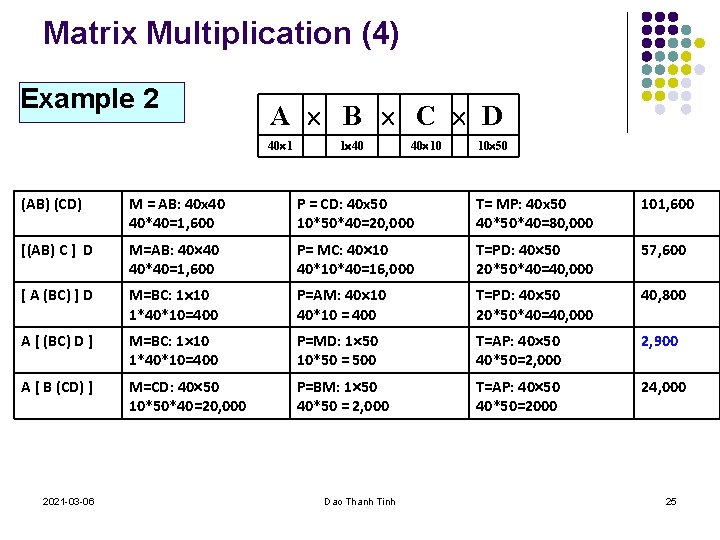
Matrix Multiplication (3) Example 2 A B C D 40 1 1 40 40 10 10 50 (AB) (CD) [(AB) C] D [A (BC)] D A [(BC) D] A [B (CD)] 2021 -03 -06 Dao Thanh Tinh 24

Matrix Multiplication (4) Example 2 A B C D 40 1 1 40 40 10 10 50 (AB) (CD) M = AB: 40 x 40 40*40=1, 600 P = CD: 40 x 50 10*50*40=20, 000 T= MP: 40 x 50 40*50*40=80, 000 101, 600 [(AB) C ] D M=AB: 40 40 40*40=1, 600 P= MC: 40 10 40*10*40=16, 000 T=PD: 40 50 20*50*40=40, 000 57, 600 [ A (BC) ] D M=BC: 1 10 1*40*10=400 P=AM: 40 10 40*10 = 400 T=PD: 40 50 20*50*40=40, 000 40, 800 A [ (BC) D ] M=BC: 1 10 1*40*10=400 P=MD: 1 50 10*50 = 500 T=AP: 40 50 40*50=2, 000 2, 900 A [ B (CD) ] M=CD: 40 50 10*50*40=20, 000 P=BM: 1 50 40*50 = 2, 000 T=AP: 40 50 40*50=2000 24, 000 2021 -03 -06 Dao Thanh Tinh 25

Matrix Multiplication (5) Ký hiệu Mij = Ai Ai+1 . . . Aj-1 Aj , i j B[i, j] = số ít nhất phép nhân để tính Mij B[1, n] - số ít nhất phép nhân để tính 2021 -03 -06 Dao Thanh Tinh A 1 A 2. . . An 26

Matrix Multiplication (6) Suppose Mij = (Ai Ai+1. . . Ak) (Ak+1. . . Aj-1 Aj) B[i, j]k = B[i, k] + di-1 dkdj + B[k+1, j] B[i, j] = min { B[i, j]k: i k < j } = 2021 -03 -06 min { B[i, k] + di-1 dkdj + B[k+1, j] } Dao Thanh Tinh 27

Matrix Multiplication (7) Mij = (Ai Ai+1. . . Ak) (Ak+1. . . Aj-1 Aj) B[i, j] = min { B[i, k] + di-1 dkdj + B[k+1, j] } d 0 d 1 d 2 d 3 d 4 40 10 50 0 1600 800 2900 0 400 900 0 20, 000 0 B[i, i] =0, i =1, . . , 4; B[1, 2] = min {B[1, 1] + B[2, 2] + d 0 d 1 d 2} = 1600 B[2, 3] = min {B[2, 2] + B[3, 3]+ d 1 d 2 d 3} = 400 B[3, 4] = min {B[3, 3] + B[4, 4]+ d 2 d 3 d 4} = 20, 000 B[1, 3]=min{B[1, 1]+B[2, 3]+d 0 d 1 d 3, B[1, 2]+B[3, 3]+d 1 d 2 d 3=min{800, 2000} = 8000 B[2, 4]=min{B[2, 2]+B[3, 4]+d 1 d 2 d 4, B[2, 3]+B[4, 4]+d 1 d 3 d 4=min{22, 000, 900} = 900 B[1, 4] =min{B[1, 1]+B[2, 4]+d 0 d 1 d 4, B[1, 2]+B[3, 4]+d 0 d 2 d 4, B[1, 3]+B[4, 4]+d 0 d 3 d 4} =min{2900, 41600, 20400} = 2900 2021 -03 -06 Dao Thanh Tinh 28

Matrix Multiplication (8) 1. for i = 1 to n do B[[i, i] = 0; 2. for t = 1 to n-1 do for i =1 to n-t do B[i, i+t] { = min B[i, k]+B[k+1, i+t] +di-1 dkdi+t: i k i+t -1 } DC[i, i+t] = chỉ số k mà tại đó tìm được B[i, i+t]; 3. output B[1, n]; Complexity: 2021 -03 -06 Dao Thanh Tinh O(n 3) 29

Matrix Multiplication (9) void Viết biểu thức(i, j : Chỉ số); if (i=j) Viết( ‘A’, i) else k : = DC[i, j]; Viết(‘(‘); Viết biểu thức(i, k); Viết(‘*’); Viết biểu thức(k+1, j ); Viết(‘)‘); 2021 -03 -06 Dao Thanh Tinh 30

Longest Monotonous Subsequence Problem: Cho dãy có n số S={X(1), X(2), . . . , X(n)}. Hãy tìm dãy con đơn điệu không giảm dài nhất S* S S* = {X(p 1), X(p 2), . . . , X(pk)}, nghĩa là X(p 1) X(p 2) . . . X(pk), với p 1 < p 2 <. . . < pk, k max 2021 -03 -06 Dao Thanh Tinh 31

Longest Monotonous Subsequence (2) Algorithm: L[i] = số phần tử trong dãy con đơn điệu dài nhất của dãy Si = { X(1), X(2), . . . , X(i) } có X(i) đứng sau cùng Ví dụ, dãy X có n=5: 12, 16, 5, 9, 6 L= 1, 2, 2 The length of longest monotonous subsequence k = max { L[1], . . , L[n] } 2021 -03 -06 Dao Thanh Tinh 32

Longest Monotonous Subsequence (3) Algorithm: Kí hiệu L[i] là số phần tử trong dãy con đơn điệu dài nhất của dãy Si = { X(1), X(2), . . . , X(i) } có X(i) đứng sau cùng L[1] = 1 L[i] = max { L[j]: X(j) X(i), j<i } + 1; nếu X(j)>X(i), 1 j<i: đặt L[i] = 1; 2021 -03 -06 Dao Thanh Tinh 33

Longest Monotonous Subsequence (4) Algorithm: Đặt X(0) = ; L[0] = 0; Kí hiệu L[i] là số phần tử trong dãy con đơn điệu dài nhất của dãy Si = { X(0), X(1), X(2), . . . , X(i) } có X(i) đứng sau cùng L[1] = 1 L[i] 2021 -03 -06 = max { L[j]: X(j) X(i), 0 j<i } + 1; Dao Thanh Tinh 34

Longest Monotonous Subsequence (5) CS 1 2 3 4 5 6 7 8 9 X= 12 16 5 9 6 4 7 11 5 L= 1 2 2 1 3 4 2 7/3 8/4 d/k 3/1 5/2 L[p] = max{L[i]: i=1, 2, . . , n} = 4, p =8 d 3 = ? d 3 = max { j<d 4=8: L[j] = 3, X[j] X[8] } d 2 = ? d 2 = max { j<d 3=7: L[j] = 2, X[j] X[7] } d 1 = ? d 1 = max { j<d 2=5: L[j] = 2, X[j] X[5] } 2021 -03 -06 Dao Thanh Tinh d 4= 8 d 3 = 7 d 2 = 5 d 1 = 3 35

Longest Monotonous Subsequence (6) CS 1 2 3 4 5 6 7 8 9 X= 12 16 5 9 6 4 7 11 5 L= 1 2 2 1 3 4 2 7/3 8/4 d/k 3/1 5/2 L[p] = max{L[i]: i=1, 2, . . , n} = 4, p =8 d 4= 8 d 3 = ? d 3 = max { j<d 4=8: L[j] = 3, X[j] X[8] } d 3 = 7 d 2 = ? d 2 = max { j<d 3=7: L[j] = 2, X[j] X[7] } d 2 = 5 d 1 = ? d 1 = max { j<d 2=5: L[j] = 2, X[j] X[5] } d 1 = 3 Xác định dãy Ký hiệu L[p] = max { L[i]: i=1, 2, . . . , n} d. L[p] = p; for k= L[p] 1 downto 1 do dk =max {j: L[j]=k, j<dk+1, X(j)<X(dk+1)} output X(d 1), X(d 2), . . . , X(d. L[p]) 2021 -03 -06 Dao Thanh Tinh 36

Longest Common Subsequence Given a sequence X = {x 1, x 2, . . . , xn}. Sequence S = {s 1, s 2, . . . , sk} is a subsequence of X if there exists a strictly increasing sequence i 1, i 2, . . . , ik of indices of X such that for all j = 1, 2, . . . , k: xij = sj. For example, S = {B, C, D, B} is a subsequence of X = {A, B, C, B, D, A, B} with corresponding index sequence i = 2, 3, 5, 7 2021 -03 -06 Dao Thanh Tinh 37

Longest Common Subsequence (2) Given two sequences X and Y, a sequence S is a common subsequence of X and Y if Z is a subsequence of both X and Y. Example: X = { A, B, C, B, D, A, B } and Y = { B, D, C, A, B, A } S={ B, C, B, A } is common to both X and Y, has length 4. S={ B, C, B, A } is an LCS of X and Y 2021 -03 -06 Dao Thanh Tinh 38

Longest Common Subsequence (3) Problem: Given two sequences X = { x 1, x 2, . . . , xm } and Y = { y 1, y 2, . . . , yn } find a maximum-length common subsequence S of X and Y 2021 -03 -06 Dao Thanh Tinh 39

Longest Common Subsequence (4) Characteristics: Given two sequences X(m) = { x 1, x 2, . . . , xm } and Y(n) = { y 1, y 2, . . . , yn } S = S(k) = {s 1, s 2, . . . , sk } be any LCS of X and Y. 1) sk= xm = yn S(k-1) = {s 1, s 2, . . . , sk-1} is LCS of X(m-1) and Y(n-1). 2) xm yn, zk xm S is an LCS of X(m-1) and Y 3) xm yn, zk yn S is an LCS of X and Y(n-1) 2021 -03 -06 Dao Thanh Tinh 40

Longest Common Subsequence (5) Remark: Given X(m) = { x 1, x 2, . . . , xm } and Y(n) = { y 1, y 2, . . . , yn } define S = S(k) = LCS { X(m), Y(n) } if xm = yn if xm yn, 2021 -03 -06 append xm to S(k-1) where S(k-1) is LCS of X(m-1) and Y(n-1). S’ = LCS{ X(m-1), Y} S” = LCS{X, Y(n-1) } if |S’| > |S”| then S = S’ else S = S” Dao Thanh Tinh 41

Longest Common Subsequence (6) Computing the length of an LCS: Given X(m) = { x 1, x 2, . . . , xm } and Y(n) = { y 1, y 2, . . . , yn } define S = S(k) = LCS { X(m), Y(n) }, B[i, j] = lenght( LCS{X(i), Y(j)} ) formula: i>0, j>0: if xi = yj, B[i, j] = B[i-1, j-1] + 1 if xi yj, B[i, j] = max { B[i-1, j], B[i, j-1] } i=0 j=0 B[i, j] = 0 2021 -03 -06 Dao Thanh Tinh 42

Longest Common Subsequence (7) Computing the length of an LCS: Given X(m) = { x 1, x 2, . . . , xm } and Y(n) = { y 1, y 2, . . . , yn } define S = S(k) = LCS { X(m), Y(n) }, B[i, j] = lenght( LCS{X(i), Y(j)} ) Algorithm: for (j=1; j n; j++) B[0, j] = 0; for (i=1; i m; i++) B[i, 0] = 0; for (i=1; i m; i++) for (j=1; j n; j++) if (xi yj) B[i, j] = max { B[i-1, j], B[i, j-1] } else B[i, j] = B[i-1, j-1] + 1; 2021 -03 -06 Dao Thanh Tinh 43

Longest Common Subsequence (8) Constructing an LCS: X = { A, B, C, B, D, A, B } and Y = { B, D, C, A, B, A } j= i 0 S = { B, C, B, A } 1 2 3 4 5 6 7 2021 -03 -06 xi A B C B D A B Dao Thanh Tinh 0 1 2 3 4 5 6 yj B D C A B A 0 0 0 1 1 1 1 2 2 0 1 1 2 2 3 3 0 1 2 2 3 3 4 0 1 2 2 3 4 4 44

Longest Common Subsequence (9) 1. k = B[m, n]; i=m; j=n; 2. while (i>1)& (j>1) 1) if (X[i]=Y[j]) S[k]=X[i]; i=i-1; j=j-1; else if(B[i, j-1]>B[i-1, j]) j=j-1; else i=i-1; 2) k = k – 1; j= i 0 1 2 3 4 5 6 Complexity of Algorithm is O(mn) 2021 -03 -06 7 Dao Thanh Tinh xi A B C B D A B 0 1 2 3 4 5 6 yj B D C A B A 0 0 0 1 1 1 1 2 2 0 1 1 2 2 3 3 0 1 2 2 3 3 4 0 1 2 2 3 4 4 45

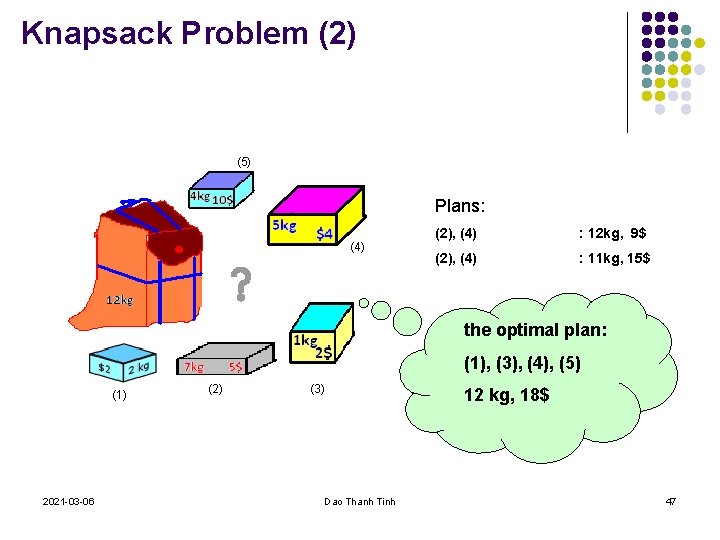
Knapsack Problem Cho túi có sức chứa W, W – số nguyên dương, tập S có n đồ vật trọng lượng: w 1, w 2, . . . , wn giá trị v 1, v 2, . . . , vn. Xếp như những đồ vật nào vào túi để tổng giá trị các đồ vật trong túi là lớn nhất? 2021 -03 -06 Dao Thanh Tinh 46

Knapsack Problem (2) (5) Plans: (4) (2), (4) : 12 kg, 9$ (2), (4) : 11 kg, 15$ the optimal plan: (1), (3), (4), (5) (1) 2021 -03 -06 (2) (3) Dao Thanh Tinh 12 kg, 18$ 47

Knapsack Problem (3) 0 -1 Knapsack Problem 2021 -03 -06 Dao Thanh Tinh 48

Knapsack Problem (4) B[i, j] giá trị lớn nhất có được với túi có sức chứa j và xem xét các đồ vật 1, 2, . . . , i i = 0, 1, . . . , n j = 0, 1, . . . , W Giá trị chứa trong túi bằng 0 khi: • Không sử dụng đồ vật nào, • hoặc sức chứa của túi bằng 0 j = 0, . . . , W i = 0, . . , n 2021 -03 -06 B[0, j] = 0, B[i, 0] = 0, Dao Thanh Tinh 49

Knapsack Problem (5) B[i, j] j = 0, . . . , W i = 0, . . , n B[0, j] = 0, B[i, 0] = 0, giá trị lớn nhất có được với túi có sức chứa j và xem xét các đồ vật 1, 2, . . . , i i = 0, 1, . . . , n j = 0, 1, . . . , W Tính B[i, j]: 1) Không thể sử dụng đồ vật i, do j<wi: B[i, j] = B[i-1, j] 2) Không sử dụng đồ vật i vì không lợi: B[i, j-wi] + vi < B[i-1, j] c) Sử dụng đồ vật i vì có lợi: B[i-1, j-wi] + vi ≥ B[i-1, j] B[n, T] – giá trị lớn nhất của đồ vật được xếp vào túi. 2021 -03 -06 Dao Thanh Tinh 50

Knapsack Problem (6) B[i, j] giá trị lớn nhất có được với túi có sức chứa j và xem xét các đồ vật 1, 2, . . . , i i = 0, 1, . . . , n j = 0, 1, . . . , W j = 0, . . . , W i = 0, . . , n B[0, j] = 0, B[i, 0] = 0, j<Wi: B[i, j] = B[i-1, j] j≥Wi: B[i, j] = max { B[i-1, j], B[i-1, j-wi]+vi} B[n, T] – giá trị lớn nhất của đồ vật được xếp vào túi. 2021 -03 -06 Dao Thanh Tinh 51

Knapsack Problem (7) (5) B[i+1, j] = max { B[i, j], B[i, j-wi+1]+vi+1} B[0, j] = 0, j=0, . . . , W B[i, 0] = 0, i=0, . . n j = 0, . . . , w 1 -1 j = w 1, . . . , W (4) B[1, j] = 0, B[1, j] = v 1 (2) (1) i 2021 -03 -06 j= (3) 0 1 2 3 4 5 6 7 8 9 10 11 12 0 0 0 0 1 0 0 2 2 2 0 0 2 2 2 5 5 7 7 3 0 2 2 4 4 5 7 7 9 9 9 4 0 2 2 4 4 4 6 6 8 8 9 9 9 5 0 2 2 4 10 12 12 14 14 14 18 Dao Thanh Tinh 52

Knapsack Problem (8) for (i=0; i≤n; i++) B[i, 0] = 0; for (j=0; j≤W; j++) B[0, j] = 0; for (i=1; i≤n; i++) for (j=1; j≤W; j++) if (wi<j) B[i, j] = B[i-1, j]; else B[i, j] = max { B[i-1, j], B[i-1, j-wi+1]+vi+1}; Complexity 2021 -03 -06 The method described does not tell which subset gives the optimal solution. O(n. W) Dao Thanh Tinh 53

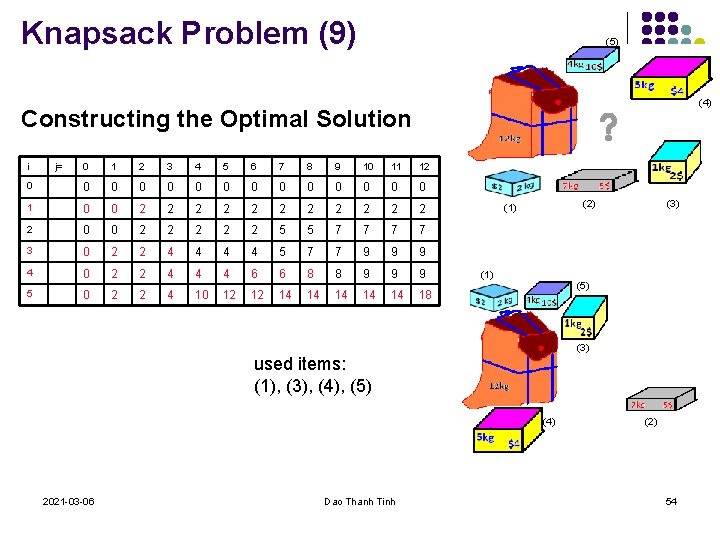
Knapsack Problem (9) (5) (4) Constructing the Optimal Solution i j= 0 1 2 3 4 5 6 7 8 9 10 11 12 0 0 0 0 1 0 0 2 2 2 0 0 2 2 2 5 5 7 7 3 0 2 2 4 4 5 7 7 9 9 9 4 0 2 2 4 4 4 6 6 8 8 9 9 9 5 0 2 2 4 10 12 12 14 14 14 18 (2) (1) (3) (1) (5) (3) used items: (1), (3), (4), (5) (4) 2021 -03 -06 Dao Thanh Tinh (2) 54

Knapsack Problem (10) Constructing the Optimal Solution i j= 0 1 2 3 4 5 6 7 8 9 10 11 12 0 0 0 0 1 0 0 2 2 2 0 0 2 2 2 5 5 7 7 3 0 2 2 4 4 5 7 7 9 9 9 4 0 2 2 4 4 4 6 6 8 8 9 9 9 5 0 2 2 4 10 12 12 14 14 14 18 remark: if B[i, j] > B[i-1, j] if B[i, j] = 0 2021 -03 -06 item ith is used in optimal solution: items 1, 2, . . , i are not used capacity amount j is not used Dao Thanh Tinh 55

Knapsack Problem (11) Constructing the Optimal Solution j = W; i = n; k = 0; while (B[i, j]>0) { while (B[i, j] = B[i 1, j]) i = i 1; k = k + 1; cs[k] = i; j = j a[i]; i = i 1; } Output cs[k], cs[k-1], . . . , cs[1] – chỉ số các đồ vật được dùng 2021 -03 -06 Dao Thanh Tinh 56

Knapsack Problem (12) Bounded Knapsack Problem 2021 -03 -06 Dao Thanh Tinh 57

Knapsack Problem (13) Bounded Knapsack Problem for (i=0; i≤n; i++) B[i, 0] = 0; for (j=0; j≤W; j++) B[0, j] = 0; for (i=1; i≤n; i++) for (j=1; j≤W; j++) if (wi<j) B[i, j] = B[i-1, j]; else B[i, j] = max { B[i-1, j-kwi]+kvi, k= 0, 1, 2, . . . , ci, j-kwi>0}; 2021 -03 -06 Dao Thanh Tinh 58

Knapsack Problem (14) Unbounded Knapsack Problem 2021 -03 -06 Dao Thanh Tinh 59

Knapsack Problem (15) Unbounded Knapsack Problem for (i=0; i≤n; i++) B[i, 0] = 0; for (j=0; j≤W; j++) B[0, j] = 0; for (i=1; i≤n; i++) for (j=1; j≤W; j++) if (wi<j) B[i, j] = B[i-1, j]; else B[i, j] = max { B[i-1, j-kwi]+kvi, k= 0, 1, 2, . . . , j-kwi>0}; 2021 -03 -06 Dao Thanh Tinh 60

Knapsack Problem (16) Ví dụ 4: Cho tập S có n đồ vật với giá trị a 1, a 2, . . . , an. Chia S thành 2 phần sao cho độ lệch tổng giá trị các đồ vật giữa hai phần là ít nhất. 2021 -03 -06 Dao Thanh Tinh 61

Knapsack Problem (17) Lời giải: Kí hiệu M = a 1 + a 2 +. . . + an và T = [M/2]. Giải bài toán cái túi với sức chứa của túi là T, khối lượng các đồ vật {a 1, a 2, . . . , an}, giá trị các đồ vật {a 1, a 2, . . , an}. Kí hiệu S 1 là tập các đồ vật đưa vào túi và S 2 = SS 1. Hai phần {S 1, S 2} là lời giải của bài toán trong ví dụ 4. Chứng minh: Kí hiệu T 1 là tổng các đồ vật thuộc S 1, T 2 là tổng các đồ vật thuộc S 2: T 1 T T 2, T 1+T 2 = M Giả sử có phương án tốt hơn chia đồ vật thành 2 phần V 1, V 2: 0 V 2 – V 1 < T 2 – T 1 Cộng 2 vế các BĐT: V 1 – V 2 0 và V 1 + V 2 = 2 T, suy ra V 1 T (*). Cộng 2 vế các BĐT: T 1– T 2 < V 1 – V 2 và T 1+ T 2 = V 1 + V 2, suy ra T 1 < V 1 Nghĩa là: T 1< V 1 T. Điều này vô lý vì T 1 là tổng con lớn nhất không quá T! 2021 -03 -06 Dao Thanh Tinh 62

Knapsack Problem (18) Chứng minh: Kí hiệu T 1 là tổng các đồ vật thuộc S 1, T 2 là tổng các đồ vật thuộc S 2: T 1 T T 2, T 1+T 2 = M Giả sử có phương án tốt hơn chia đồ vật thành 2 phần V 1, V 2: 0 V 2 – V 1 < T 2 – T 1 Cộng 2 vế các BĐT: V 1 – V 2 0 và V 1 + V 2 = 2 T, suy ra V 1 T (*). Cộng 2 vế các BĐT: T 1– T 2 < V 1 – V 2 và T 1+ T 2 = V 1 + V 2, suy ra T 1 < V 1 Nghĩa là: T 1< V 1 T. Điều này vô lý vì T 1 là tổng con lớn nhất không quá T! 2021 -03 -06 Dao Thanh Tinh 63

Bài tập Bài toán: Giả thiết A = {A 1, A 2, . . . , An} là tập hợp giá trị các đồng xu, Ai Z+, i {1, 2, . . . , n}. Có thể giả thiết A 1 < A 2 <. . . < An và mỗi loại giá trị có số đồng xu không hạn chế. Cho số nguyên dương T, hãy xây dựng công thức tính số ít nhất các đồng xu cần lấy để đạt giá trị T. (Có thể xét hai trường hợp: A 1=1 và A 1>1) 2021 -03 -06 Dao Thanh Tinh 64

Bài tập (2) Xét trường hợp A 1 = 1. Kí hiệu: F (j) là số đồng xu ít nhất phải dùng để có tổng j, F(j) j. Để có thể dùng được loại đồng xu thứ i: Ai j và chỉ dùng khi: F( j-Ai) + 1 < F( j ) Dùng đến loại đồng xu thứ i và dùng k đồng xu loại thứ i k*Ai j và Khi này: F( j-k*Ai) + k < F( j ) F(j) : = F(j-k*Ai) + k D(j) : = i; Ghi nhớ là thực sự dùng đến loại thứ i 2021 -03 -06 Dao Thanh Tinh 65

Bài tập (3) Do vậy có công thức: F(j) = min { F( j-k*Ai) + k : k = 0, . . . , j/Ai }: i=1, . . . , n} 2021 -03 -06 Dao Thanh Tinh 66

Bài tập (4) Truy ngược: For i: =1 to n SL[i] : = 0 j: = T While j > 0 i : = D(j) While (j>0) & ( F(j) = F(j – Ai) SL[i] = SL[i] + 1 j = j – Ai Output SL[1], . . . , SL[n]; 2021 -03 -06 Dao Thanh Tinh 67

Bài tập (5) Xét trường hợp A 1 > 1? 2021 -03 -06 Dao Thanh Tinh 68

Bài tập (6) Cho dãy biểu thức f = A 1 * A 2 *. . . * An-1 * An trong đó, Aj là số nguyên dương, j = 1, 2, . . . , n. Hãy thay phép toán “*” bằng phép “+” hoặc “ ” để f có giá trị không âm nhỏ nhất. 2021 -03 -06 Dao Thanh Tinh 69