Dynamic Programming Dynamic Programming Dynamic programming is a

Dynamic Programming

Dynamic Programming • Dynamic programming is a quantitative analysis technique that has been applied to large, complex problems that have sequences of decisions to be made. (Dynamic programming is a method for solving optimization problems) • Dynamic programming divides problems into a number of decision stages; the outcome of a decision at one stage affects the decision at each of the next stages (the idea: Compute the solutions to the subproblems once and store the solutions in a table, so that they can be reused (repeatedly) later).

Applications • The technique is useful in a large number of multiperiod business problems, such as smoothing production employment, allocating capital funds, allocating salespeople to marketing areas, and evaluating investment opportunities.

Dynamic programming differs from linear programming in two ways: First, there is no algorithm (like the simplex method) that can be programmed to solve all problems. Dynamic programming is, instead, a technique that allows us to break up difficult problems into a sequence of easier subproblems, which are then evaluated by stages. Second, linear programming is a method that gives single-stage (one time period) solutions. Dynamic programming has the power to determine the optimal solution over a one-year time horizon by breaking the problem into 12 smaller one-month horizon problems and to solve each of these optimally. it uses a multistage approach.

Four Steps of Dynamic Programming 1. Divide the original problem into subproblems called stages. 2. Solve the last stage of the problem for all possible conditions or states. 3. Working backward from the last stage, solve each intermediate stage. This is done by determining optimal policies from that stage to the end of the problem (last stage). 4. Obtain the optimal solution for the original problem by solving all stages sequentially.

Two types of DP problems v. In this lecture we show to solve two types of dynamic programming problems: network and nonnetwork. 1. The shortest-route problem is a network problem that can be solved by dynamic programming. 2. The knapsack problem is an example of a nonnetwork problem that can be solved using dynamic programming.

The Knapsack Problem

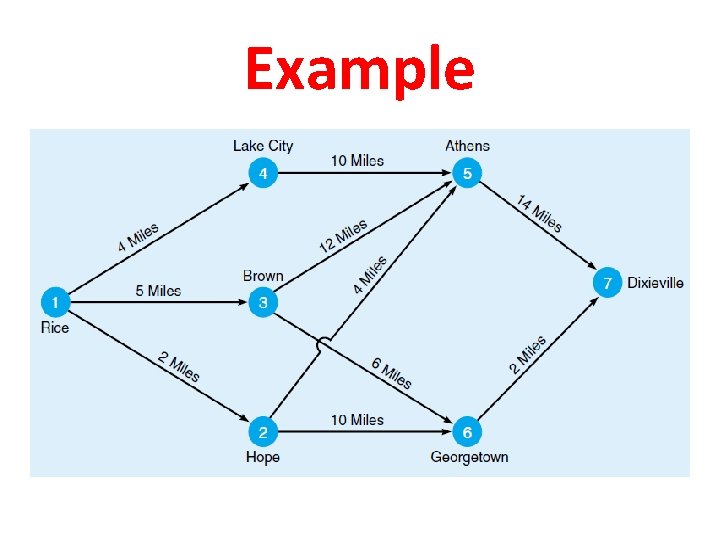
SHORTEST-ROUTE PROBLEM SOLVED BY DYNAMIC PROGRAMMING • Our goal : • We want to make a trip from city (1), to city(7). & • We would like to find the shortest route. • Note that: • The circles on the map, called nodes, represent cities • The arrows, called arcs, represent highways between the cities • The distance in miles is indicated along each arc

Example

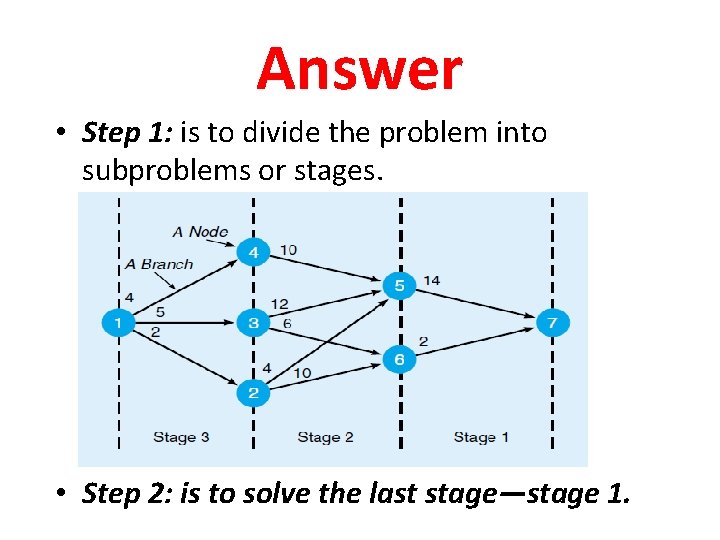
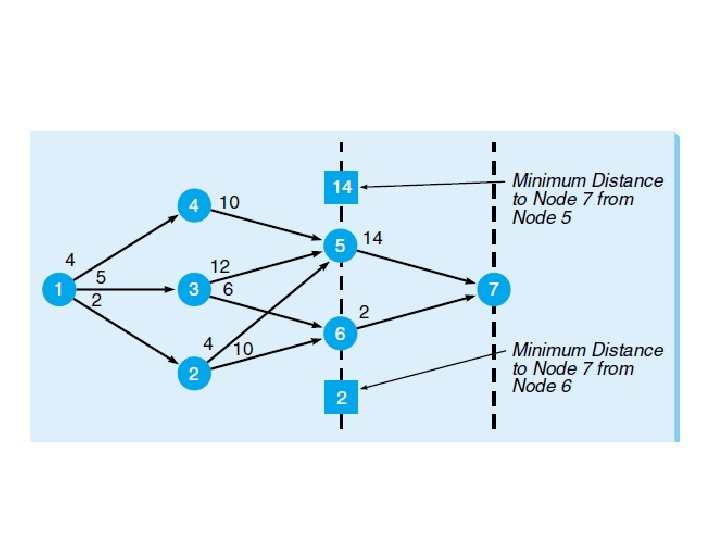
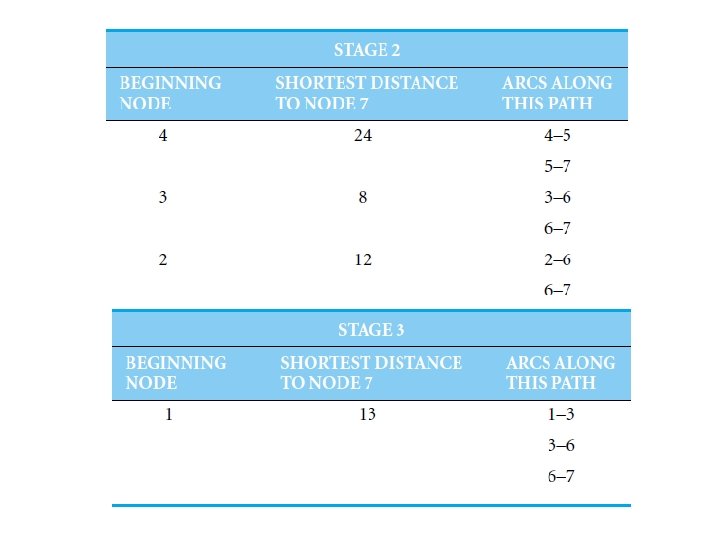
Answer • Step 1: is to divide the problem into subproblems or stages. • Step 2: is to solve the last stage—stage 1.

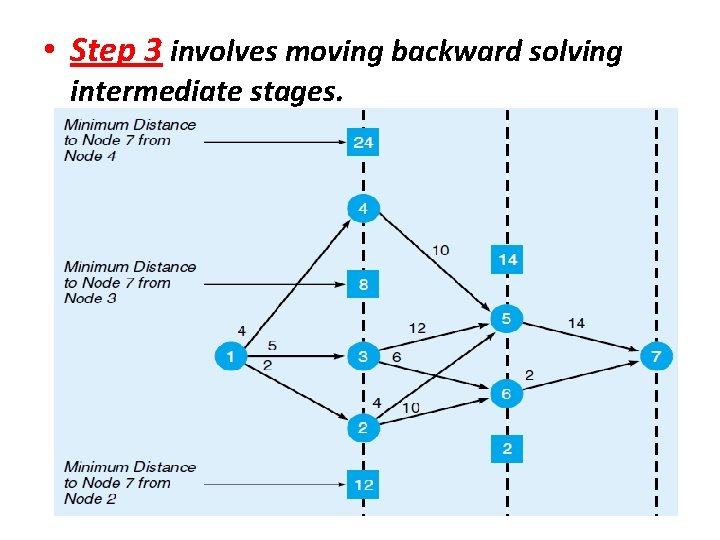
• Step 3 involves moving backward solving intermediate stages.

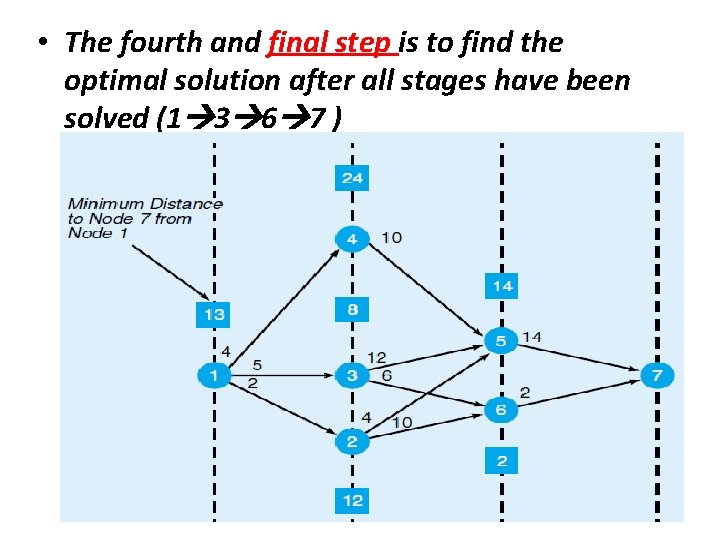
• The fourth and final step is to find the optimal solution after all stages have been solved (1 3 6 7 )

DYNAMIC PROGRAMMING TERMINOLOGY 1. Stage: a period or a logical subproblem. 2. State variables: variables possible beginning situations or conditions of a stage. These have also been called the input variables. 3. Decision variables: variables alternatives or possible decisions that exist at each stage. 4. Decision criterion: criterion a statement concerning the objective of the problem. 5. Optimal policy: a set of decision rules, developed as a result of the decision criteria, that gives optimal decisions for any entering condition at any stage. 6. Transformation: normally, an algebraic statement that reveals the relationship between stages.

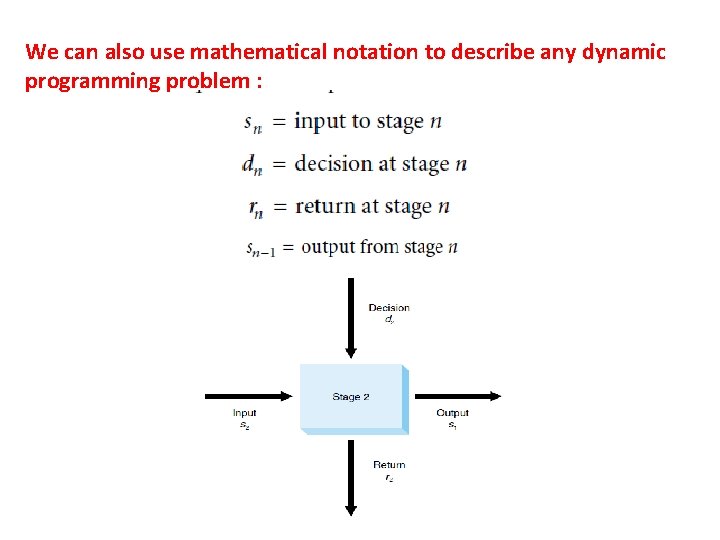
We can also use mathematical notation to describe any dynamic programming problem :

Transformation Function The transformation function allows us to go from one stage to another. The transformation function for stage 2, t 2, converts the input to stage 2, s 2, and the decision made at stage 2, d 2, to the output from stage 2, s 1. Because the transformation function depends on the input and decision at any stage, it can be represented as t 2 (s 2, d 2).

KNAPSACK PROBLEM • The “knapsack problem” involves the maximization or the minimization of a value, such as profits or costs • We can place different types of items in the knapsack. Our objective is to place items in the knapsack to maximize total value without breaking the knapsack because of too much weight or a similar restriction

Types of Knapsack Problems There are many kinds of problems that can be classified as knapsack problems. • Choosing items to place in the cargo compartment of an airplane and Selecting which payloads to put on the next NASA Space Shuttle are examples. The restriction can be volume, weight, or both. • Some scheduling problems are also knapsack problems. For example, we may want to determine which jobs to complete in the next two weeks. The two-week period is the knapsack, and we want to load it with jobs in such a way as to maximize profits or minimize costs. The restriction is the number of days or hours during the two-week period. ( Hw#1 solve one example for this type)

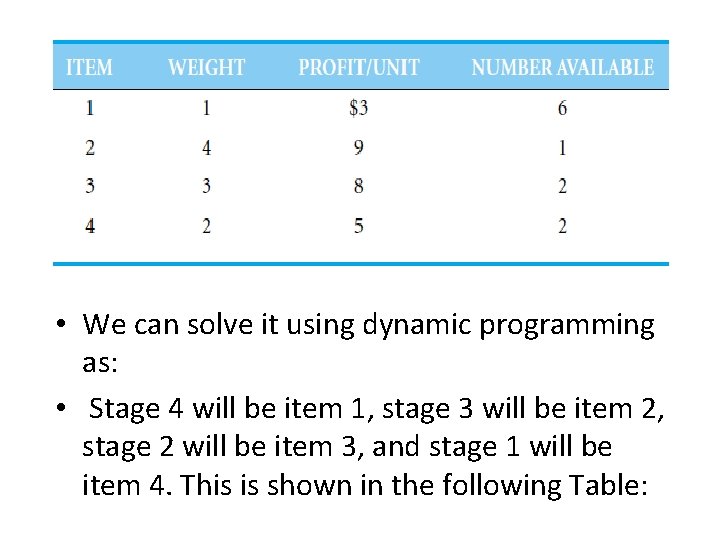
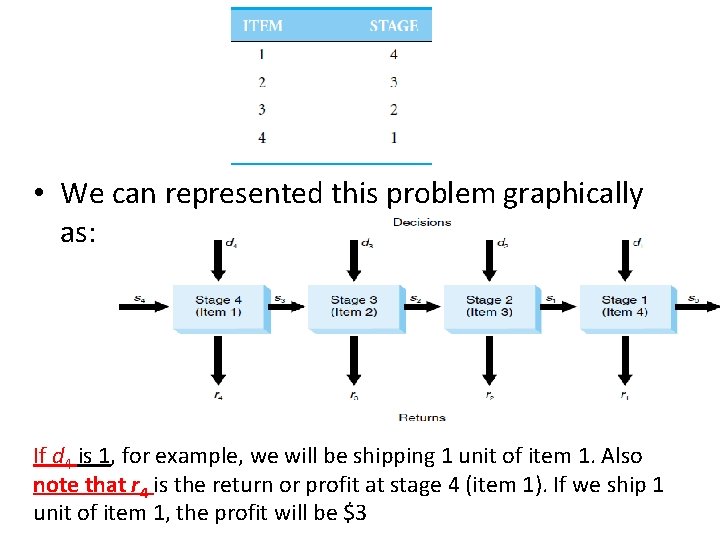
Example Rob Roller owns and operates Roller’s Air Transport Service, which ships cargo by plane to most large cities in the United States and Canada. The remaining capacity for one of the flights from Seattle to Vancouver is 10 tons. There are four different items that Rob can ship between Seattle and Vancouver. Each item has a weight in tons, a net profit in thousands of dollars, and a total number of that item that is available for shipping. This information is presented in the following Table :

• We can solve it using dynamic programming as: • Stage 4 will be item 1, stage 3 will be item 2, stage 2 will be item 3, and stage 1 will be item 4. This is shown in the following Table:

• We can represented this problem graphically as: If d 4 is 1, for example, we will be shipping 1 unit of item 1. Also note that r 4 is the return or profit at stage 4 (item 1). If we ship 1 unit of item 1, the profit will be $3

• The Transformation Functions : The general transformation function for knapsack problems follows: Note that an, bn, and cn are coefficients for the problem and that dn represents the decision at stage n. This is the number of units to ship at stage

Sn-1 =Sn – ( weight )dn Note that : s 4 is 10, the total weight that can be shipped. Because s 4 represents the first item, all 10 tons can be utilized. The transformation equations for the four stages are as follows:

Sn-1 =Sn – ( weight )dn • Consider stage 3. Equation: The number of tons still available after stage 3, s 2, is equal to the number of tons available before stage 3, s 3, minus the number of tons shipped at stage 3, 4 d 3. In this equation, 4 d 3 means that each item at stage 3 weighs 4 tons

Return Function The Return Functions Next, we will look at the return function for each stage. This is the general form for the return function: rn= profit/per unit × dn Then the actual return functions are:

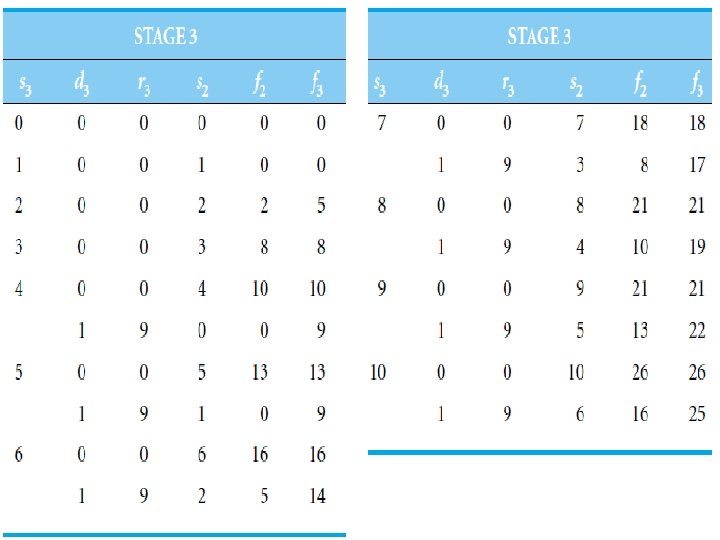
Stage-by-Stage Solution • we can solve this problem by starting with stage 1 (item 4). • The following table shows the solution for the first stage:

Note That • Because we don’t know how many tons will be available at stage 1, we must consider all possibilities. Thus the number of tons available at stage 1, s 1, can vary from 1 to 10. • The number of units that we ship at stage 1, d 1, can vary from 0 to 2. We can’t go over 2 because the number available is only 2. For any decision we compute the return at stage 1, r 1, by multiplying the number of items shipped by 5, the profit per item. The profit at this stage will be 0, 5, or 10, depending on whether 0, 1 or 2 items are shipped

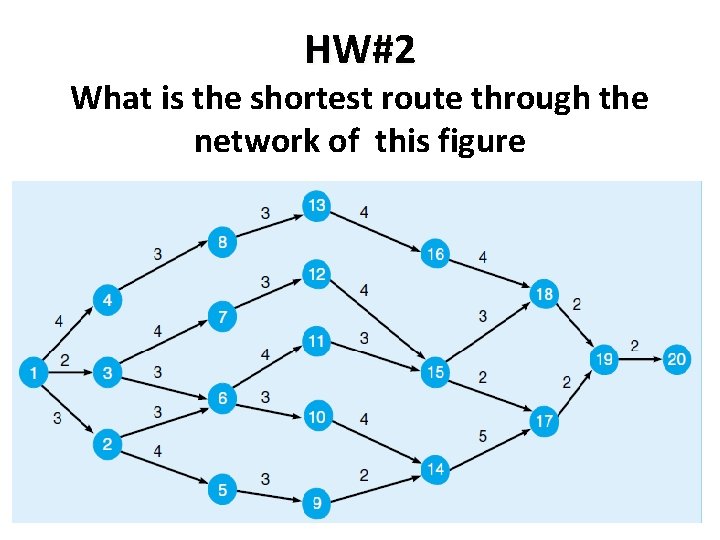
HW#2 What is the shortest route through the network of this figure

HW#3 Paige Schwartz is planning to go camping in Big Bend National Park. She will carry a backpack with food and other items, and she wants to carry no more than 18 pounds of food. The four possible food items she is considering each have certain nutritional ingredients. These items and their weights are as follows: • How many of each item should Paige carry if she wishes to maximize the total nutritional units?

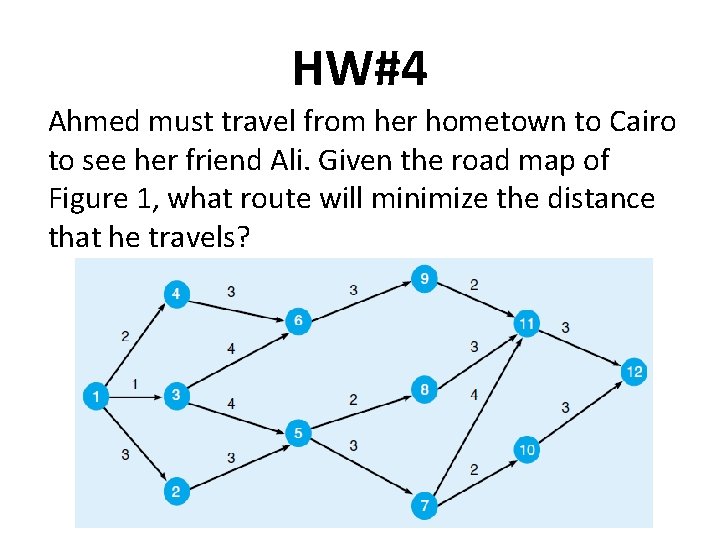
HW#4 Ahmed must travel from her hometown to Cairo to see her friend Ali. Given the road map of Figure 1, what route will minimize the distance that he travels?