CS 5243 Algorithms Dynamic Programming Dynamic Programming is

CS 5243: Algorithms Dynamic Programming

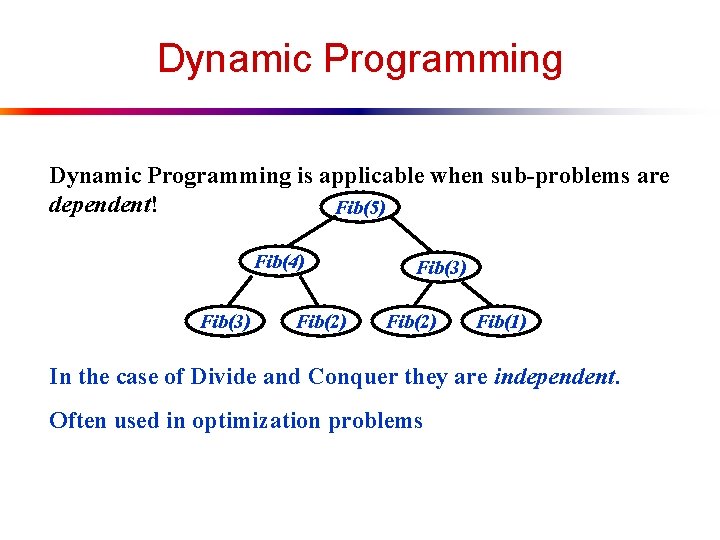
Dynamic Programming is applicable when sub-problems are dependent! Fib(5) Fib(4) Fib(3) Fib(2) Fib(1) In the case of Divide and Conquer they are independent. Often used in optimization problems

Development of a DP algorithm 1. Characterize the structure of an optimal solution 2. Recursively define the value of an optimal solution 3. Computer the value of an optimal solution 4. Construct an optimal solution from computed information Note: Dynamic programming works bottom up while a technique called Memoization is very similar but is a recursive top down method.

Memoization l. Memoization is one way to deal with overlapping subproblems n. After computing the solution to a subproblem, store in a table n. Subsequent calls just do a table lookup l. Can modify recursive alg to use memoziation: Lets do this for the Fibonacci sequence Fib(n) = Fib( n-1) + Fib( n-2) Fib(2) = Fib(1) = 1

Fibonacci Memoization Lets write a recursive algorithm to calculate Fib(n) and create an array to store subprogram results in order that they will not need to be recalculated. In memoization we recurse down and fill the array bottom up. int fib. Array[]={0, 1, 1, 0, 0, 0, 0, 0, 0} int Fib(int n){ if (fib. Array[n]>0)return( fib. Array[n]) else return (Fib(n-1)+Fib(n-2)) }

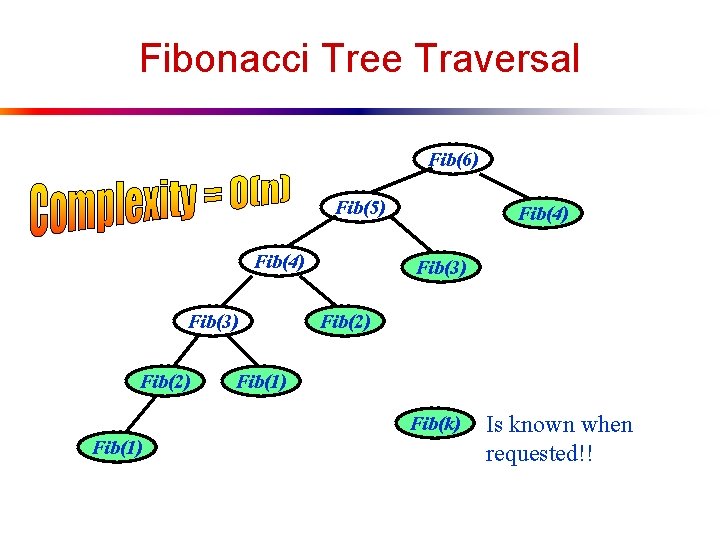
Fibonacci Tree Traversal Fib(6) Fib(5) Fib(4) Fib(3) Fib(2) Fib(1) Fib(k) Fib(1) Is known when requested!!

The DP solution to Fibonacci int Fib(int n) { // Note that this is not recursive int fib. Array[]={0, 1, 1, 0, 0, 0, 0, , 0}; for (i=3, i <= n; i++) fib. Array[i] = fib. Array[i-1]+fib. Array[i-2]; return fib. Array[n]; }

Next Problem: Matrix Multiplication Matrix-Multiply(A, B) 1. if columns[A] != rows[B] 2. then error “ incompatible dimensions” 3. else for i = 1 to rows[A] 4. 5. 6. 7. 8. return C A B do for j = 1 to columns[B] do C[i, j] = 0 for k=1 to columns[A] do C[i, j] = C[i, j]+A[i, k]*B[k, j]

Matrix-chain Multiplication problem Problem: Given a chain <A 1, A 2, A 3, . . . , An> of n matrices, where for i= 1, 2, . . . , n, matrix Ai has dimension p i-1 x p i, fully parenthesize the product A 1 A 2. . . An in a way that minimizes the number of scalar multiplications. Example: Suppose we have the following size arrays 10 x 20 * 20 x 40 * 40 x 5 then ((10 x 20 20 x 40) 40 x 5) yields then (10 x 20 (20 x 40 40 x 5)) yields 10*20*40+10*40*5=10, 000 mults 20*40*5+10*20*5=5, 000 mults Clearly parenthesizing makes a big difference!

How many parens are there? Exhaustively checking all possible parenthesizations is inefficient! Let P(n) denote the number of alternative parenthesizations of a sequence of n matrices. Hence P(1)=1 otherwise if n>2 we have The complexity of P(n) in this case is (2 n)

Optimal Parenthesization Major Observation: An optimal solution to an instance of the matrix chain multiplication problem contains within it optimal solutions to subproblems. Suppose that an optimal parenthesization of Ai. . . Aj splits the product between Ak and Ak+1. Then the parenthesization of the prefix subchain Ai. . Ak must also be optimal! The same is true for the postfix subchain. Why is this true? (A 1, A 2, A 3, . Ak)(A k+1. . , An) Optimal Cost(A 1. . An) = Cost(A 1. . Ak) + Cost(A k+1. . An) + Cost of final product

Intermediate Storage in Table As usual in DP we will store intermediate results in a table say in this case M. Let M[i, j] be the minimum # of scalar multiplications needed to computer A i. . j If the optimal soln splits A i. . j at k then M[i, j] = M[i, k] + M[k, j] + pi-1 pkpj where Ai has dim pi-1 pj Since we really do not know the value of k we need to check the j -i possible values of k. Hence

Finding the Optimal Solution Each time we find the above minimum k lets store it in an array s[i, j]. Hence s[i, j] is the value of k at which we can split the product A 1 Ai+1. . . Aj to obtain an optimal parenthesization.

The Algorithm Matrix-Chain-Order(p) n length[p]-1 for i 1 to n do m[i, j] 0 for p 2 to n // p is the chain length do for i 1 to n - p + 1 do j i + p - 1 m[i, k] for k i to j - 1 do q m[i, k] + m[k+1, j] + pi-1 pkpj if q < m[i, j] then m[i, j] q; s[i, j] k return m and s

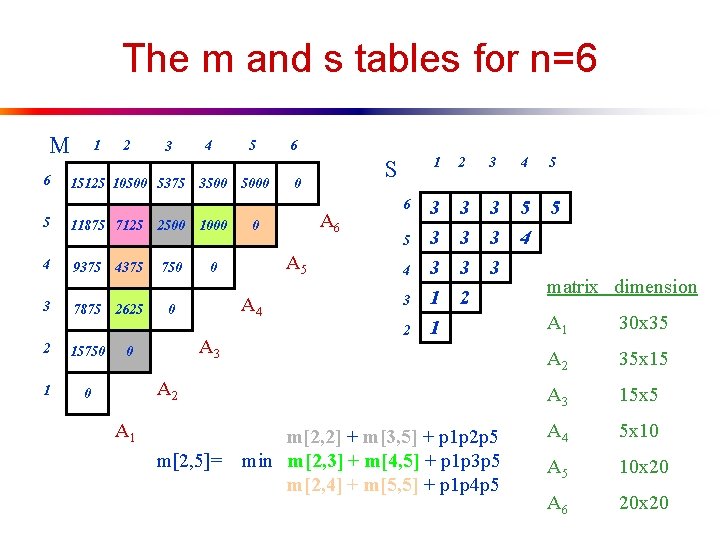
The m and s tables for n=6 M 6 5 4 3 1 2 3 15125 10500 5375 4 3500 11875 7125 2500 1000 9375 750 0 7875 2 15750 1 0 4375 2625 5000 A 3 6 S 0 A 6 0 A 5 A 4 0 0 5 6 5 4 3 2 1 2 3 4 5 3 3 3 1 1 3 3 3 2 3 3 3 5 4 5 A 2 A 1 m[2, 5]= m[2, 2] + m[3, 5] + p 1 p 2 p 5 min m[2, 3] + m[4, 5] + p 1 p 3 p 5 m[2, 4] + m[5, 5] + p 1 p 4 p 5 matrix dimension A 1 30 x 35 A 2 35 x 15 A 3 15 x 5 A 4 5 x 10 A 5 10 x 20 A 6 20 x 20

Observations 1 2 3 4 5 6 0 6 15125 10500 5375 3500 5000 5 11875 7125 2500 1000 0 4 9375 750 0 4375 3 7875 2625 2 15750 0 1 0 A 1 A 4 0 A 3 A 2 A 5 Note that we build this array from bottom up. Once a cell is filled we never recalculate it. Complexity is (n 3) Why? What is the space complexity?

Printing the Parenthezation Print. Optimal. Parens(s, i, j) The call Print. Optimal. Parens(s, 1, 6) if i = j prints the solution then print “A”; else print “(“ ((A 1( A 2, A 3))((A 4 A 5) A 6)) Print. Optimal. Parens(s, i, s[i, j]) Print. Optimal. Parens(s, s[i, j]+1, j) print “)”

Optimal Binary Search Trees The next problem is a another optimization problem. You are required to find a BST that optimizes accesses to the tree given probability of access for each item in the tree. Here are examples assume equal probabilities of 1/7. 1 1 while 2 if 2 1 if 2 do while 3 2 do 3 3 cost=15/7 2 cost=13/7 2 2 2

More Examples Cost=2. 05 1 Cost=2. 65 while Cost=1. 9 while 1 if 2 do 1 2 if do 3 2 if 3 3 while 2 do 3 2 2 3 Assuming that probabilities of access are p(do)=. 5, p(if)=. 1, p(while)=. 05 and q(0)=. 15, q(1)=. 1, q(2)=. 05, q(3)=. 05 q(0) : do : q(1) : if : q(2) : while : q(3) Cost(third tree)= 1(. 1)+2(. 5)+2(. 05)+2(. 1)+2(. 05) = 1. 9 2

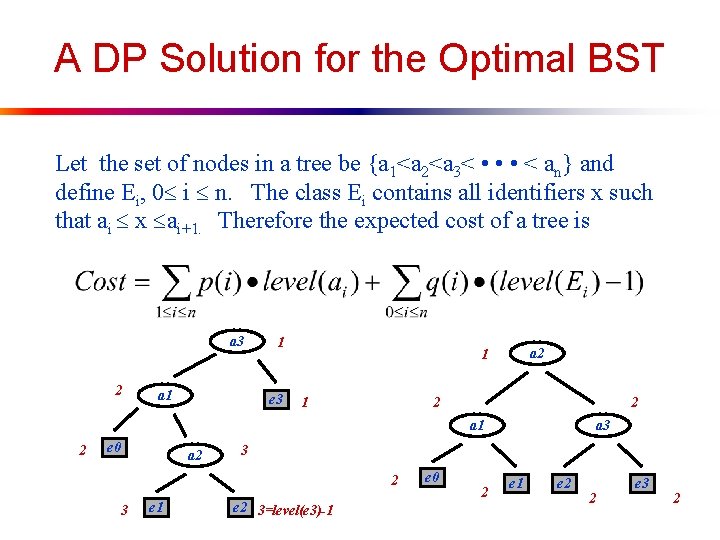
A DP Solution for the Optimal BST Let the set of nodes in a tree be {a 1<a 2<a 3< • • • < an} and define Ei, 0 i n. The class Ei contains all identifiers x such that ai x ai+1. Therefore the expected cost of a tree is a 3 2 a 1 1 e 3 a 2 1 1 2 2 a 1 2 e 0 a 2 3 e 1 a 3 e 2 3=level(e 3)-1 e 0 2 e 1 e 2 2 e 3 2

Optimal Subproblems! if Optimal Left tree Optimal Right tree This problem exhibits optimal substructure. For if the above tree is optimal then the left and right subtrees most be optimal! Optimal Substructure often implies a Dynamic Programming solution The following algorithm is based on this observation.

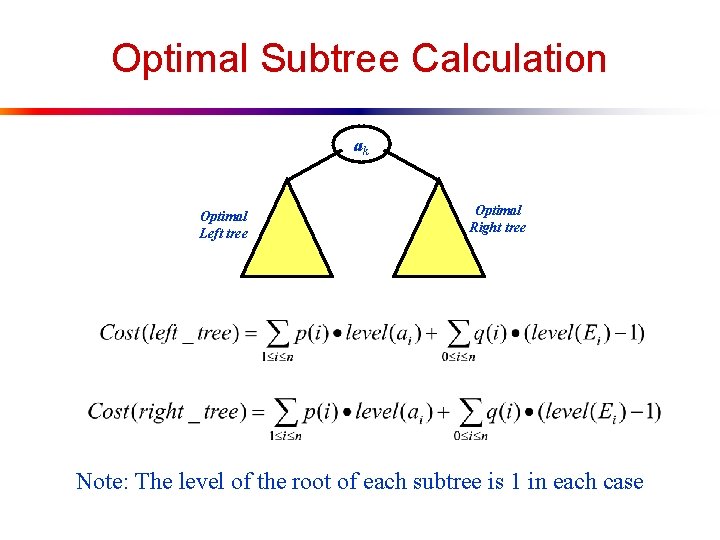
Optimal Subtree Calculation ak Optimal Left tree Optimal Right tree Note: The level of the root of each subtree is 1 in each case

Optimal Subtree ak Optimal Left tree Optimal Right tree The cost of the above entire tree in terms of the optimal subtree is p(k) + cost(left_tree) + w(0, k-1) +cost(right_tree) + + w(k, n) where

W(0, k-1) is a fix for the left tree a 3 Assuming p(i) is probability of ai the cost of left subtree by itself is 2 1 a 1 e 3 1*p(1)+2*p(2)+ 1*q(0)+2*q(1)+2*q(2) and w(0, 2) in this case is p(1) + 2 e 0 1 p(2) + q(0) + q(1) + q(2) 3 Can you see what w(0, 2) does in this case? 3 2 a 2 e 1 2 1 3 e 2 2 left subtree It adds 1 probe count to each term on the left side to account for the fact that the subtree is one node deeper! 1

Minimizing over the roots Recall that the cost of the entire tree, with ak the root, is p(k) + cost(left_tree) + w(0, k-1) +cost(right_tree) + + w(k, n) All we need to do then is to find the value of k so that the above is minimum. So we look at each tree with ak the root. a 2 a 1 ak an

Minimization formula If we use c(i, j) to represent the cost of an optimal binary search tree, tij, containing ai+1, . . . , aj and Ei, . . . , Ej, then for the tree to be optimal k must be optimally chosen so that p(k) + c(left_tree) + w(0, k-1) +c(right_tree) + + w(k, n) is minimum. So in general simplifies to

The Process The above equation can be solve sort of bottom up by so we compute all c(i, j) where j=i+1, then those that have j=i+2 etc. While we do this we record the root r(i, j) of each optimal tree. This allows us to then reconstruct the complete optimal tree.

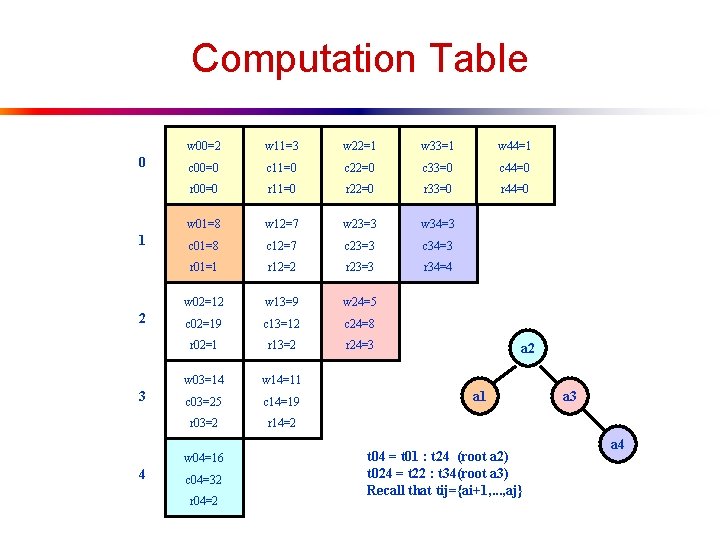
An Example Let n=4 and {a 1, a 2, a 3, a 4} be the set of nodes in a tree. Also let p(1: 4)=(3, 3, 1, 1) and q(0: 4)=(2, 3, 1, 1, 1). Here we multiply the p’s and the q’s by 16 for simplicity. So w(i, i)=q(i)=c(i, i)=0 w(0, 1) = p(1) + q(1) + w(0, 0) = 8 w(2, 3) = p(3) + q(3) + w(2, 2) = 3 c(0, 1) = w(0, 1) + min{c(0, 0+c(1, 1)} = 8 c(2, 3) = w(2, 3) + min{c(2, 2)+c(3, 3)} = 3 r(0, 1) = 1 r(2, 3) = 3 w(1, 2) = p(2) + q(2) + w(1, 1) = 7 w(3, 4) = p(4) + q(4) + w(3, 3) = 3 c(1, 2) = w(1, 2) + min{c(1, 1)+c(2, 2)} = 7 c(3, 4) = w(3, 4) + min{c(3, 3)+c(4, 4)} = 3 r(1, 2) = 2 r(3, 4) = 4

Computation Table 0 1 2 3 w 00=2 w 11=3 w 22=1 w 33=1 w 44=1 c 00=0 c 11=0 c 22=0 c 33=0 c 44=0 r 00=0 r 11=0 r 22=0 r 33=0 r 44=0 w 01=8 w 12=7 w 23=3 w 34=3 c 01=8 c 12=7 c 23=3 c 34=3 r 01=1 r 12=2 r 23=3 r 34=4 w 02=12 w 13=9 w 24=5 c 02=19 c 13=12 c 24=8 r 02=1 r 13=2 r 24=3 w 03=14 w 14=11 c 03=25 c 14=19 r 03=2 r 14=2 w 04=16 4 c 04=32 r 04=2 a 1 t 04 = t 01 : t 24 (root a 2) t 024 = t 22 : t 34(root a 3) Recall that tij={ai+1, . . . , aj} a 3 a 4

Complexity of OBST Algorithm We computer c(i, j) for j-i = 1, 2, 3, . . . , n in that order. When j-i=m there are n-m+1 c(i, j)’s to computer each of which finds the minimum of m quantities. Hence we do m(n-m+1) or mn -m 2+m operations on the mth row. So the total time is D. E. Knuth has shown that if you limit the search to the range r(i, j-1) k r(i+1, j) the computing time becomes O(n 2)